多自由度球軸承與軸的剛度耦合分析與計算*

張耀虎,馬臨超,齊山成

(1.北京新聯鐵集團股份有限公司,北京 100044;2.河南工業大學 機電學院,河南 鄭州 450000;3.鄭州機械研究所有限公司,河南 鄭州 450000)

0 引 言

目前,球軸承已經在鐵路機車、船舶、汽車、拖拉機、重型機械等動力傳動系統中得到了廣泛應用。

作為傳動系統中的重要零部件,球軸承的性能是否優良對系統的傳動精度有著重要的影響。

球軸承剛度是球軸承重要的使用性能指標之一,因此,對其剛度進行計算與分析很有必要,尤其是對球軸承的徑向剛度和軸向剛度進行計算與分析更有必要。

對球軸承剛度的計算屬于典型的非線性方程求解問題。JONES A B在Hertz球軸承的靜力學分析模型基礎上,建立了球軸承的靜力學平衡方程,即靜力學模型。

雖然在高速重載工況下,采用靜力學模型對球軸承剛度進行計算與分析,所得到的結果會與實際結果有較大的偏差;但是,無論如何,靜力學模型為軸承的分析計算提供了一種新的思路。

在靜力學平衡方程的基礎上,鄧四二[1]根據鋼球與滾道的變形協調幾何關系,推導出了軸承在負載條件下的軸向剛度和徑向剛度;在非線性范圍內,這些公式給出了負載與變形關系的表達式,同時也更好地對真實運動狀態下的軸承進行了描述。JONES A B[2]提出了一種球軸承的滾道控制理論,并將其作為運動邊界條件;同時,在對其進行計算的過程中充分考慮了摩擦的因素,豐富了軸承計算分析的方法。在此基礎上,HARRIS T A[3]提出了一種五自由度球軸承剛度矩陣的計算方法,進一步奠定了軸承動力學分析的基礎。

但是上述研究并未對球軸承的軸向自由度進行分析。同時,之前的文獻[4-12]也只是對軸承剛度做了大量研究,而在研究過程中,對軸承剛度的外部影響因素考慮較少。

因此,筆者擬從球軸承的6個自由度方向對此進行分析計算,將球軸承與軸的變形分析相結合,在考慮軸受載變形的軸承-軸剛度模型的基礎上,提出一種球軸承-軸的剛度進行計算方法;最后,將軟件計算結果與文獻對照數據進行對比,以驗證所提出的計算方法能夠對球軸承-軸的剛度進行計算。

1 軸承剛度計算與受載平衡

在球軸承中,滾動體與內外滾道的接觸變形是影響滾動軸承運轉精度和旋轉穩定性的重要因素。通常情況下,需根據赫茲理論(Hertz-Theory)[13]對軸承接觸應力進行計算。雖然Hertz的假設是點接觸,但是赫茲彈性接觸理論可以在一定程度上解決軸承接觸應力與變形的問題。

Hertz點接觸問題考慮的是兩個任意彈性曲面在初始狀態下僅一點發生接觸的情況,所以,在分析軸承接觸變形問題時要進行如下假設:

(1)接觸體是線性彈性體,且均勻各向同性,在外力作用下只發生微小變形;

(2)接觸體表面連續光滑,且接觸形式僅屬于局部接觸;

(3)接觸區長度遠小于物體表面的曲率半徑,忽略接觸區附近物體的表面曲率;

(4)接觸表面不存在摩擦力。

基于以上假設,筆者首先用二次函數來描述接觸點附近的一般曲線方程;然后假定接觸區是一個橢圓的形狀,即接觸應力呈半橢圓球函數分布;最后將彈性半空間的解引入接觸區域內,以便對其進行法向位移的計算。

1.1 球軸承-鋼球的幾何變形關系

在徑向載荷Fy、軸向載荷Fz和橫向徑向載荷Fx的共同作用下,球軸承分別產生豎直徑向變形δy、軸向變形δz、橫向徑向變形δx;

在徑向力矩載荷My、軸向力矩載荷Mz和橫向徑向載荷Mx的共同作用下,球軸承分別產生徑向旋轉位移βy、軸向旋轉位移βz、橫向徑向旋轉位移βx。其中,第i個滾動體的位置,用位置角φi表示。

球軸承的受力示意圖如圖1所示。

圖1 軸承受力示意圖

設軸承外圈與箱體固定,外圈不因載荷而產生變形,即外圈曲率中心Oo不變;第i個鋼球受載前后,內圈曲率中心Oi和外圈曲率中心Oo之間的距離分別為A0和A(φi),則其變形可以表示為:

(1)

其中,A(φi)可由變形條件表示為:

(2)

(3)

式中:δri—第i個鋼球受載后的徑向變形;δzi—第i個鋼球受載后的軸向變形;α0—鋼球與滾道的初始接觸角。

鋼球的受載變形示意圖如圖2所示。

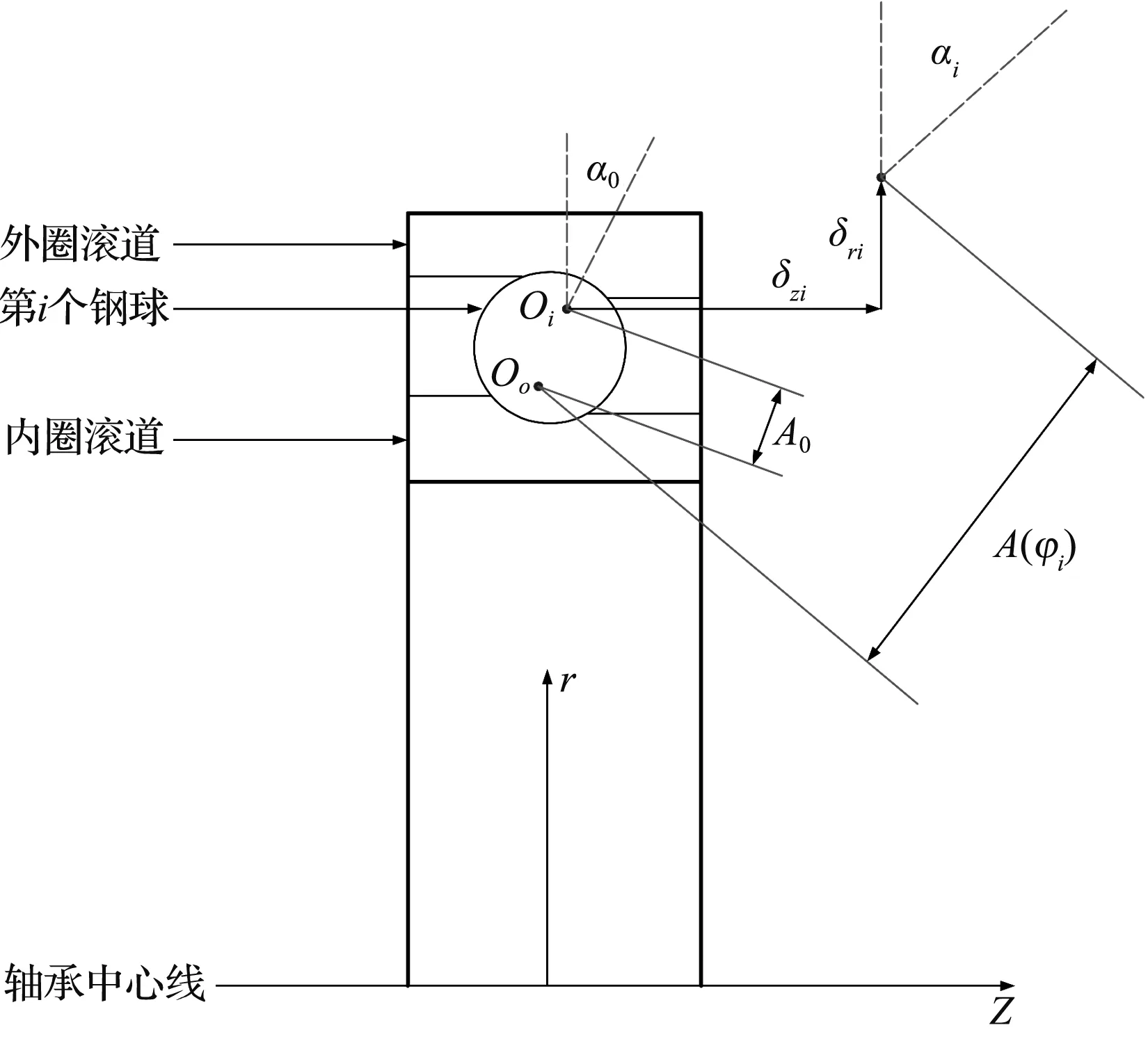
圖2 鋼球受力變形示意圖

鋼球受載變形和軸承坐標系下各自由度方向變形的協調關系,如圖3所示。

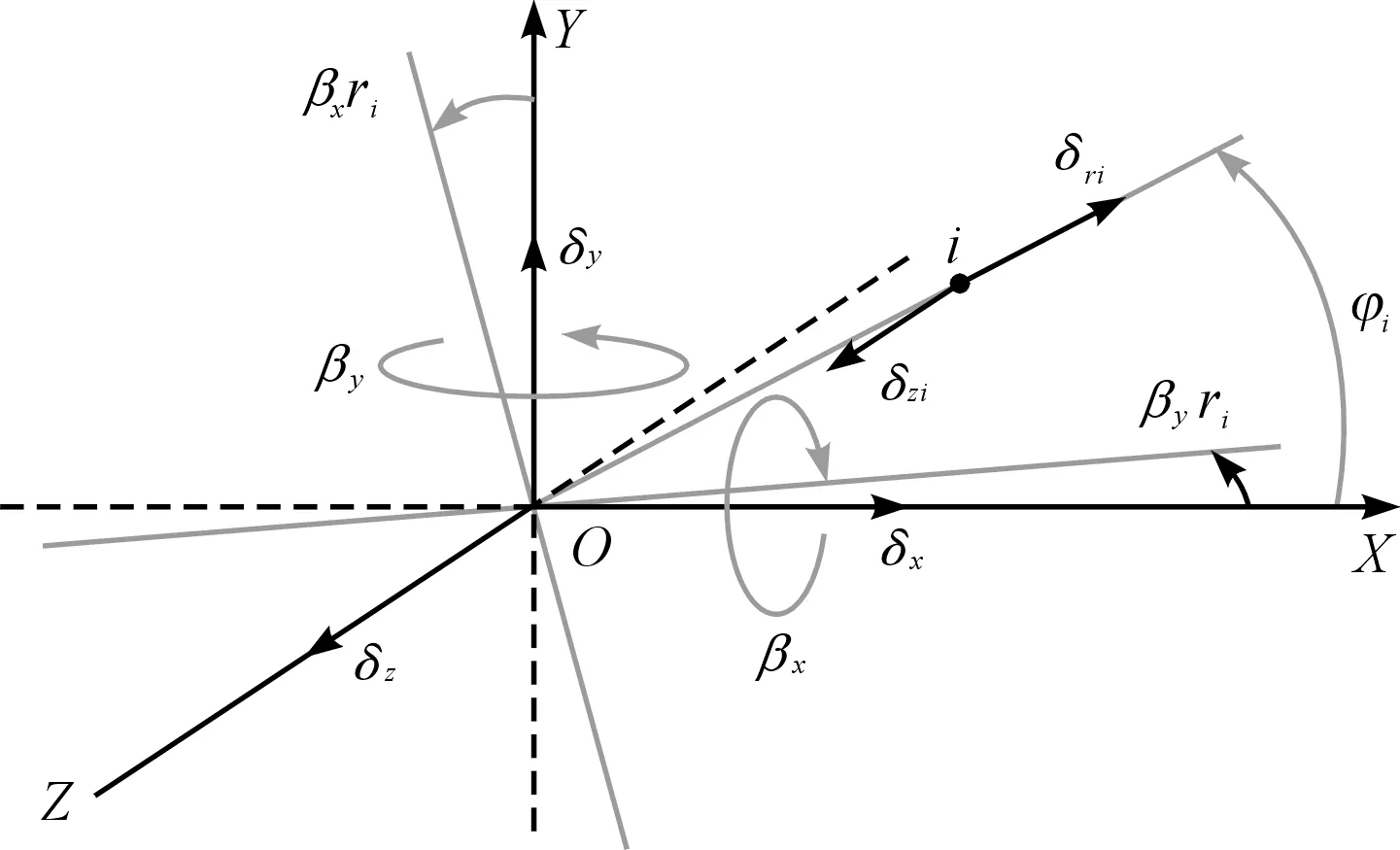
圖3 鋼球變形協調示意圖

由圖3可得:

(4)

式中:ri—內圈滾道曲率半徑;rL—滾道與鋼球的間隙。

1.2 球軸承的受載變形與剛度計算

在確定了軸承與鋼球各方向上的變形位移關系后,還需要確定軸承與鋼球各方向上的力平衡關系。

根據赫茲(Hertz)彈性接觸理論,第i個鋼球受載與變形的關系表達如下:

(5)

式中:Qi—軸承中第i個鋼球與滾道局部接觸點處的法向載荷;Kn—與接觸材料、幾何參數相關的參數。

當兩彈性體的接觸為線接觸[14-18]時,n取10/9;當兩彈性體的接觸為點接觸時,n取1.5。

筆者將每個不同位置、不同接觸角、不同位置角的鋼球的載荷與變形統一到軸承整體的坐標軸上,再通過對每個鋼球的不同方向載荷的疊加,得到球軸承整體徑向力載荷為Fym、軸向載荷Fzm、橫向徑向載荷Fxm、徑向力矩載荷為Mym、軸向力矩載荷Mzm、橫向徑向力矩載荷Mxm,最終可得軸承的力與變形平衡方程:

(6)

式中:αi—第i個鋼球受載變形后的接觸角。

(7)

(8)

球軸承整體受到徑向力載荷為Fym、軸向載荷Fzm、橫向徑向載荷Fxm、徑向力矩載荷為Mym、軸向力矩載荷Mzm、橫向徑向力矩載荷Mxm,會分別產生δym、δzm、δxm、βym、βzm、βxm這6個方向的變形位移。

各個載荷分別對6個方向的位移求偏導,便可以得到軸承剛度的表達式,其矩陣形式如下:

(9)

值得注意的是,軸承剛度不是一個常量,它會隨著位移(或載荷)的變化而變化,因此,在提到軸承剛度的時候,應該指出它與對應的位移或者載荷,否則就沒有意義。

方程組很顯然是一個非線性方程組。經過實測,該方程組選擇使用牛頓-拉弗森(Newton-Raphson)[19,20]迭代效率最高。在編寫雅各比矩陣的時候,最好將矩陣每一項寫出,不建議使用編譯器自帶的函數求解雅各比矩陣。

假設在擺線齒錐齒輪傳動系統中,軸承受到六自由度載荷Qb,此時的軸承剛度為Kb,那么可得此軸承受載變形平衡方程,以求解各自由度方向的變形δb,即:

(10)

至此,便得到了軸承剛度的表達與軸承受載變形平衡方程。以載荷作為輸入參數進行方程求解,便可以得到六自由度變形和剛度矩陣。

1.3 滾動體接觸相關參數的計算

當鋼球載荷為Q時,其法向接觸變形δr可以寫為:

(11)

式中:G—柔度系數。

對于內、外滾道接觸,公式如下:

(12)

鋼球與兩個滾道之間的法向趨近量如下:

δn=δi+δo=(Gi+Go)Q2/3

(13)

聯立式(11～13),即有:

(14)

式中:E1，E2—接觸材料的彈性模量;∑ρ1，∑ρ2—接觸體的曲率和函數;Dw—鋼球直徑;fi—溝曲率半徑系數;fo—外圈滾道溝曲率半徑系數;dm—軸承節圓直徑;α—初始接觸角。

2 軸剛度計算與受載平衡

軸采用梁模型進行數學建模,對不同梁模型,目前有歐拉-伯努利(Euler-Bernoulli)梁模型和鐵木辛柯(Timoshenko)梁模型。其中,鐵木辛柯梁考慮了常剪應變,而歐拉梁則假定剪切剛度無限大,不發生剪應變。

具體而言,二者雖然都采用平截面假定,但對于變形前,垂直于中軸線的截面,歐拉模型在變形后仍保持與中軸線垂直;鐵木辛柯梁模型則認為二者不再垂直,出現一個剪應變項。

從應用上看,若梁的跨徑比大于5,梁通常是彎曲主控的,采用歐拉梁模型模擬;若跨徑比小于5的梁,剪切變形明顯,宜采用鐵木辛柯梁。此處,筆者將采用歐拉-伯努利梁進行梁單元的建模。

筆者設軸為兩節點梁單元,z方向表示梁單元的軸向,x和y表示梁單元的橫向和縱向;A、B表示兩個梁單元的兩個節點位置,那么該梁單元的廣義的坐標如下:

Us1={AB}T
A={xAyAzAθxAθyAθzA}
B={xByBzBθxBθyBθzB}

(15)

梁單元示意圖如圖4所示。

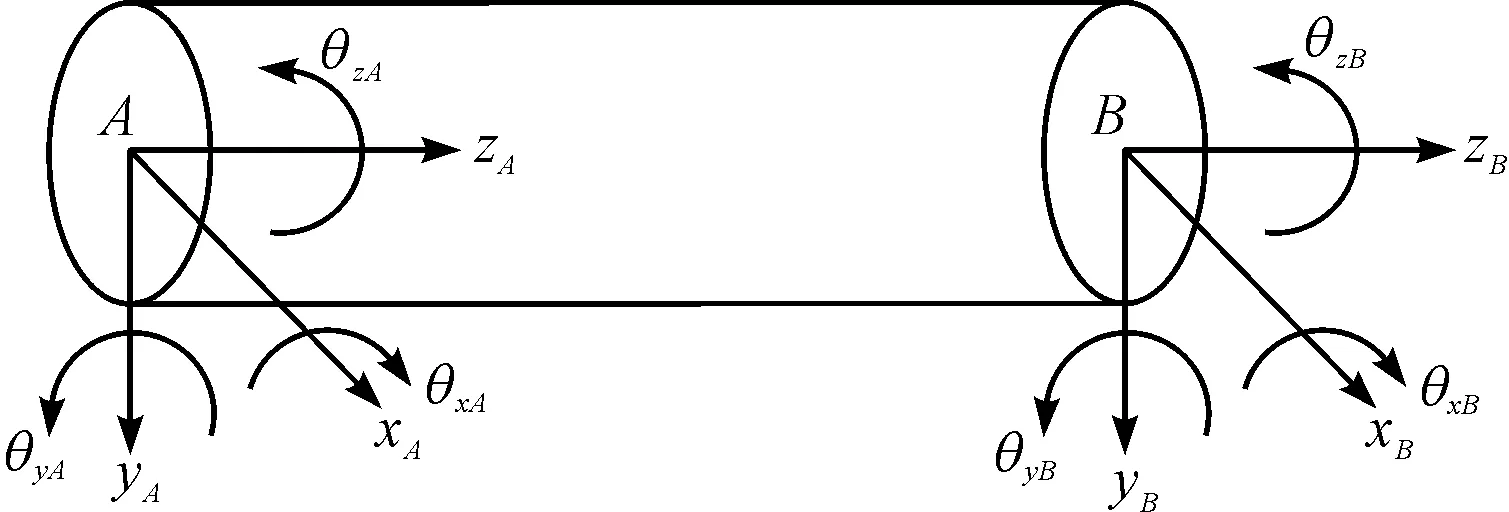
圖4 梁單元示意圖

根據材料力學理論,經典的Euler-Bernoulli梁單元的剛度矩陣如下:

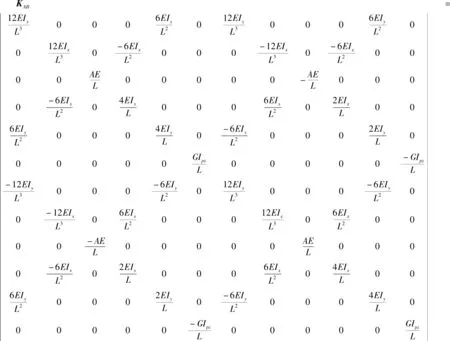
(16)

式中:E—彈性模量;G—剪切模量;A—梁的橫截面積,mm2;Ix，Iy，Iz—軸x,y,z方向的慣性矩;Ipz—軸的極慣性矩。

變量具體表達如下:

(17)

式中:ν—材料的泊松比。

用此剛度矩陣便可以描述功率輸入軸AB兩節點梁單元的剛度。主對角線的12個元素分別由A節點6個主方向的剛度和B節點6個主方向的剛度組成。

設節點A處載荷QA和節點B處的載荷QB為:

(18)

將QA、QB作為主對角線元素,便可以得到載荷矩陣QAB:

QAB=

(19)

根據剛度的定義,即力與變形的關系,便可以得到在載荷QAB作用下,梁AB節點處廣義坐標Us1下的變形為:

(20)

梁的受力平衡方程為:

FAB=KAB·δAB

(21)

通過求解該方程,便可以得到變形δAB。

3 軸承-軸系統受載變形

3.1 計算原理

根據結構力學的知識,可采用結構矩陣分析法對軸承-軸系統受載變形進行分析。結構矩陣分析的兩種基本方法是矩陣位移法(剛度法)和矩陣力法(柔度法)。

矩陣位移法在計算中采用節點位移作為基本未知量,矩陣力法則采用多余力作為基本未知量。在結構矩陣分析法中,運用矩陣進行計算,不僅能使公式緊湊,形式上規格統一,而且便于計算過程程序化。因此,筆者在此處采用矩陣位移法進行分析。

在桿件結構的矩陣位移法中,把復雜的構件當作有限多個單元的集合,各單元彼此在節點處連接,從而形成整體。因此,筆者先把結構進行拆解形成有限多個單元節點,繼而對各單元進行分析,建立單元的剛度方程用來描述力與變形的關系;再根據變形的協調條件,將離散的單元恢復為原構件系統,進而得到整體結構的剛度方程。通過這樣一分一合的過程,就把復雜的結構計算問題轉化為簡單的單元分析與綜合問題了。

因此,解決問題的方法分為兩個大步驟:

(1)單元分析。研究單元的剛度矩陣;

(2)整體分析。考慮單元的集合,研究整體方程的組成原理和求解方法。

在梁單元材料[21,22]的力學性能和材料性能確定的前提下,當梁單元受到多個方向的力的作用時,由于梁單元受載變形具有獨立性,便可以獨立地計算梁單元多個方向上的受載變形。

一般情況下,梁單元的材料剛度為靜剛度,即不會隨著載荷的變化而變化。例如,對圖5桿結構進行分析時,首先需要先將桿結構拆分成兩個梁單元進行分析,得到梁單元①和梁單元②的剛度矩陣后,通過矩陣的定位疊加,最后得到梁整體的剛度矩陣,進而得到該結構的載荷與力。

3.2 分析與計算

根據前文可知,設軸拆分后的每個軸段的幾何參數和材料參數相同,則每個軸段的剛度表達相同,且都能用歐拉-伯努利(Euler-Bernoulli)梁模型的剛度矩陣表達。

各單元耦合示意圖如圖5所示。

圖5 單元耦合示意圖

節點AB梁單元剛度矩陣可以簡化為:

(22)

節點BC梁單元剛度矩陣可以簡化為:

(23)

將節點AB梁單元剛度和節點BC梁單元剛度進行疊加耦合,軸的剛度矩陣可以重新表達為:

(24)

筆者把軸承1、軸承2安裝在軸節點A、C位置,只要在軸上對應節點處進行剛度矩陣疊加即可。設軸承1與軸承2的剛度矩陣分別為Kb1、Kb2,矩陣大小均為6×6,表示每個自由度方向的位移。

由于軸承中心線與軸的中線重合,筆者通過坐標旋轉將軸承坐標繞著z軸旋轉η,使軸承的剛度表達坐標與軸坐標Us1一致;將軸承1的剛度和軸承2的剛度通過坐標變換矩陣轉換到軸坐標系下,即:

(25)

M(ab)=|M11M12M13|

(26)

式中:M—坐標旋轉矩陣,表示某矩陣繞著向量a旋轉角度b。

(27)

(28)

(29)

(30)

設在坐標系Us1內,施加到軸上的載荷為Q,則軸承-軸模型受載變形可表達為:

(31)

(32)

式中:Q1，Q2，Q3—3個節點處的六自由度載荷。

軸承-軸受載變形的平衡方程為:

(33)

式中:δ1,δ2,δ3—軸上3個節點處的六自由度變形。

需要注意的是,如若涉及復雜空間幾何,需將各個部件統一到同一坐標系下,再進行疊加耦合。

4 軸承實例驗證

4.1 軸承剛度驗證

筆者以代號6210的深溝球軸承為例,即接觸角等于零的角接觸球軸承,滾子直徑為12.7 mm;軸承節圓直徑為70 mm;滾子數量為10;內圈溝渠率系數為0.515;外圈溝渠率系數為0.515,選取其徑向剛度進行對照驗證;

再以代號7210B的角接觸球軸承為例,即滾子直徑為12.7 mm;軸承節圓直徑為70 mm;滾子數量為15;內圈溝渠率系數為0.515;外圈溝渠率系數為0.525,選其軸向剛度進行對照驗證。

軸承徑向剛度對比結果如圖6所示。

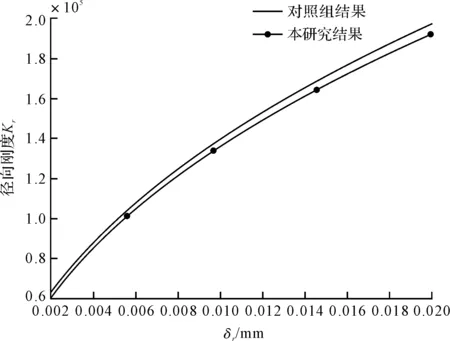
圖6 軸承徑向剛度對比結果

軸承軸向剛度對比結果如圖7所示。

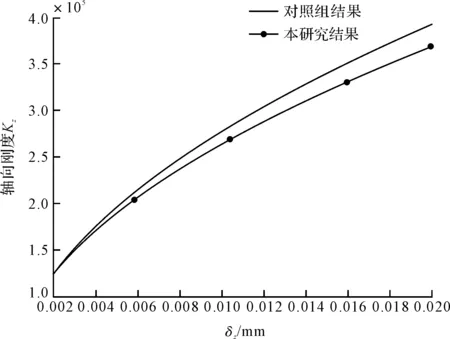
圖7 軸承軸向剛度對比結果

圖(6,7)中,筆者將上述計算結果與文獻數據結果[23]進行了對比,結果表明,軸承徑向剛度和軸向剛度的誤差范圍在7%～10%之間,均在可接受的范圍之內。

4.2 軸剛度驗證

筆者首先設置軸的參數,然后對其進行計算,再利用有限元軟件對各個計算結果進行比對,結果顯示,各結果之間完全一致。

軸的初始計算參數如表1所示。

表1 軸參數表

由于軸的剛度只與軸的幾何參數和材料參數相關,筆者設節點距坐標原點的距離為dz,得到有限元輸出的軸剛度,如表2所示。

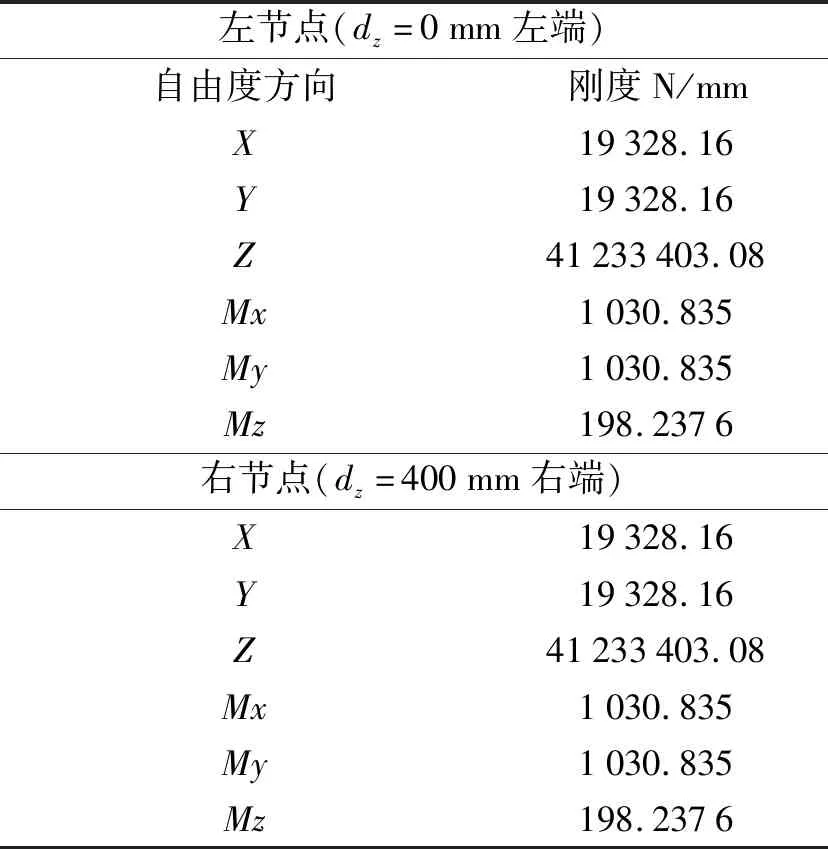
表2 有限元軸剛度輸出表

以下矩陣為該節輸出數據的1～6列:

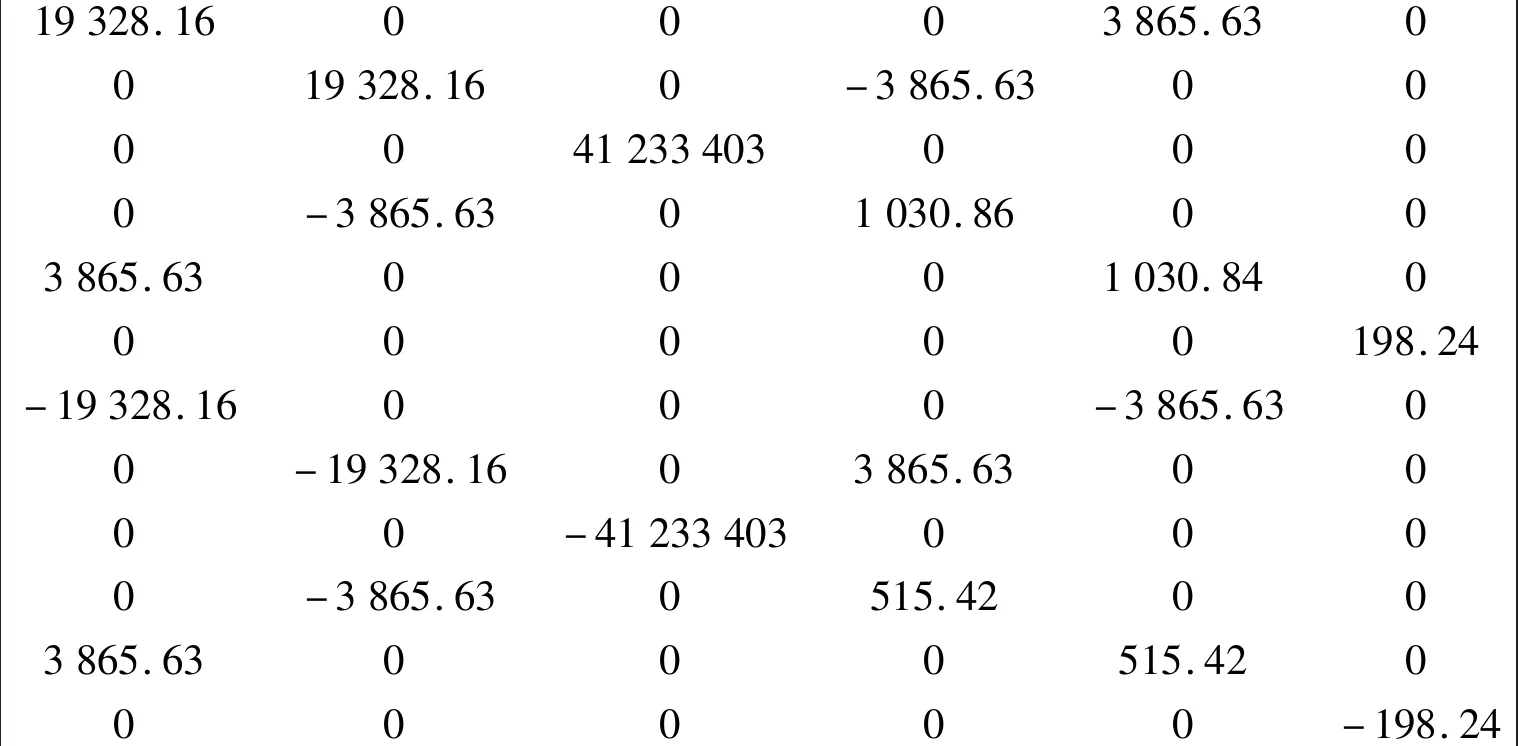
以下矩陣為該節輸出數據的7～12列:

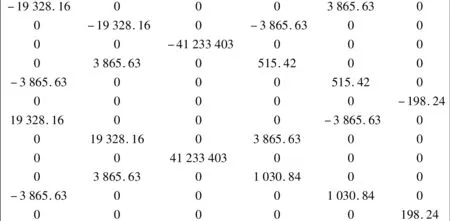
該節中使用的坐標系與有限元中的坐標系一致,矩陣中主對角線元素即軸上主方向上的剛度值,誤差可忽略不計。

4.3 軸承-軸模型剛度驗證

在上述各步驟分析的基礎上,筆者進行軸承-軸模型系統的剛度耦合驗證。

筆者在X方向輸入載荷1 000 N,在Y方向輸入載荷1 000 N,輸入位置在軸的中點處;在同等條件下,輸入載荷在X方向輸入載荷1 500 N,在Y方向輸入載荷1 500 N,載荷施加位置在軸中點處。

軸承-軸系統的分析模型如圖8所示。

圖8 軸承-軸分析模型

當X=1 000 N,Y=1 000 N時,模型各節點變形的計算結果與對照數據(文獻數據)對比情況,如表3所示。

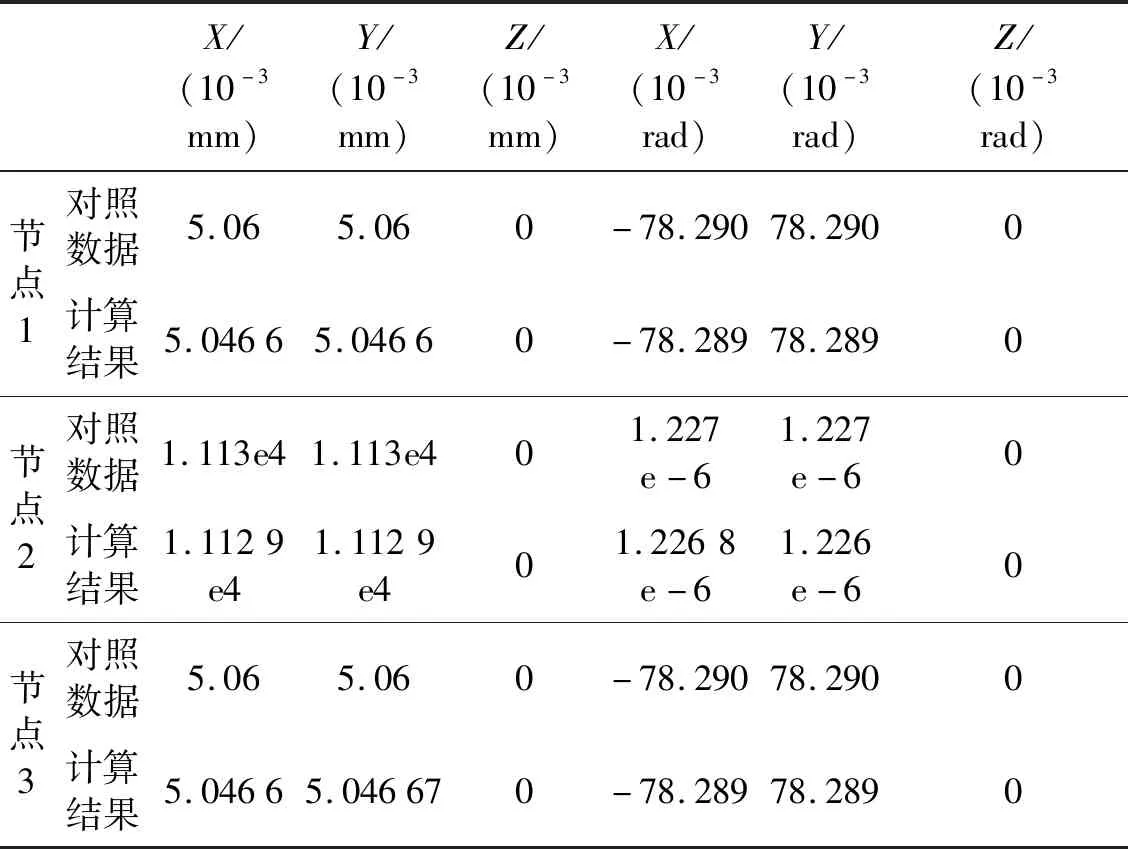
表3 模型各節點變形結果對照表

當X=1 500 N,Y=1 500 N時,模型各節點變形的計算結果與對照數據(文獻數據)對比情況,如表4所示。

表4 模型各節點變形結果對照表

5 結束語

因為單一條件下球軸承的載荷-變形分析結果在理論和實際上存在偏差,并且以往研究者在分析球軸承時未考慮軸的受載變形影響,所以,筆者結合材料力學、結構力學、復雜桿件耦合以及變形協調與力平衡原則,構建了一種考慮軸受載變形的軸承-軸剛度模型,具體為:

基于赫茲接觸理論以及變形協調與力平衡原則,構建了軸承剛度計算模型;基于歐拉梁模型,構建了軸剛度計算模型;基于材料力學與結構力學理論,構建了軸承-軸剛度耦合模型;

在此基礎上,筆者實現了對軸與軸承的耦合分析,并將軟件計算結果與文獻對照數據進行了對比,驗證了所提出的計算方法能夠對球軸承-軸的剛度進行計算。

研究結論如下:

(1)在非重載條件下,軸承-軸剛度模型以及其計算方法是可行的,計算結果是準確的;

(2)在重載條件下,由于軸承剛度的計算數值存在一定誤差,因此會影響模型計算結果的準確性;

(3)考慮了軸上點載荷對傳動系統中軸-軸承的影響,為受載情況下軸承剛度的計算提供了一種方法。

在后續的研究過程中,為獲得更加貼合實際的計算數據,筆者將在齒輪箱傳動系統等非線性系統基礎上,進一步考慮溫度、變形、摩擦等因素對實驗結果的影響,以期為傳動系統的動力學分析提供理論基礎。