七軸全地面起重機電液助力轉向系統(tǒng)能耗分析*

杜 恒,洪 越,劉曉陽,舒 月,李雨錚

(1.福州大學 機械工程及自動化學院,福建 福州 350108;2.福州大學 流體動力與電液智能控制福建省高校重點實驗室,福建 福州 350108)

0 引 言

隨著全球能源問題與環(huán)境問題的日益突出,重型車輛/起重機的節(jié)能逐步成為工業(yè)和軍事領域密切關注的焦點。但由于電液助力轉向系統(tǒng)存在高能耗、低效率的問題,因此對重型車輛/起重機的轉向系統(tǒng)能耗進行分析是很有必要的,可以為以后的節(jié)能方案研究提供理論依據(jù)。近年來,許多學者針對液壓系統(tǒng)及轉向系統(tǒng)的能耗研究做了大量的工作[1-4]。

重型車輛/起重機多軸轉向系統(tǒng)由多組閥控雙串聯(lián)助力缸液壓系統(tǒng)組成,所以可借鑒一般液壓系統(tǒng)研究方法。學者們已經(jīng)在這方面做了許多寶貴的研究。MANRING N D等人[5]通過對開放式四通閥控制雙桿雙作用線性對稱缸模型的研究,分析了閥控液壓系統(tǒng)效率并且獲得對稱缸的無量綱效率圖,得到了線性液壓執(zhí)行機構效率相當?shù)偷慕Y論。該研究為典型的閥控缸能耗分析提供了方法。ZIMMERMAN J D等人[6]基于挖掘機的典型工作循環(huán),分析了有關負載敏感挖掘機液壓系統(tǒng)的能耗,并進一步分析了挖掘機各種操作過程下的能量消耗以及各部分的能量分配,如執(zhí)行機構、控制閥、液壓泵等。

以上針對常見液壓系統(tǒng)的研究方法對分析多軸電液助力轉向系統(tǒng)提供了很好的借鑒作用。

在研究影響轉向系統(tǒng)能耗的因素方面,DAHER N等人[7]基于重型車輛轉向系統(tǒng)的閥控單缸模型,分析了轉向系統(tǒng)的能耗,發(fā)現(xiàn)傳統(tǒng)閥控液壓系統(tǒng)的能量損失主要集中在閥口處。李九靈等人[8]基于電液助力轉向系統(tǒng),研究了各主要參數(shù)在不同路況下的能耗變化規(guī)律,進而找到了對電液助力轉向系統(tǒng)(EHPS)系統(tǒng)能耗起最大影響的關鍵參數(shù);WELLENZOHN M等人[9]對液壓、電液、電動3種不同類型轉向系統(tǒng)的結構進行了分析,并分析了3種轉向系統(tǒng)的能耗。但是上述研究都是針對單軸的轉向系統(tǒng),并未從整車的角度分析多軸轉向系統(tǒng)的能耗特性。

車輛的能耗分析應以某一駕駛循環(huán)為基準,我國常用的車輛能耗測試循環(huán)為新歐洲駕駛循環(huán)(new European driving cycle,NEDC)與全球輕型車測試循環(huán)(world light vehicle test cycle,WLTC)[10-13]。在車輛轉向系統(tǒng)的能耗分析中,駕駛循環(huán)還應包含轉向信息。但是,現(xiàn)有常用的駕駛循環(huán)并沒有包含轉向信息,難以直接用于分析轉向系統(tǒng)能耗。因此,基于NEDC,加入與之匹配的轉向循環(huán),可以組成一個分析轉向系統(tǒng)能耗的駕駛循環(huán)。

在分析單軸轉向系統(tǒng)能耗之后,研究學者結合車輛行駛工況對多軸轉向系統(tǒng)進行了研究。江浩斌等人[14]設計了一種新型電控液壓助力轉向系統(tǒng)(electronically controlled hydraulic power steering,ECHPS)系統(tǒng),在怠速、加速、高速直行、低速轉角等的工況下,仿真分析了ECHPS系統(tǒng)的功耗。GUPTA V V等人[15]基于城市駕駛循環(huán),對比了EHPS系統(tǒng)與發(fā)動機驅動的轉向系統(tǒng)的能耗,并在車輛中進行了試驗測試,得到了轉向系統(tǒng)的能耗。YU L Y等人[16]根據(jù)實際車輛的行駛情況,并考慮了轉角及轉向阻力信號,從而測得了車輛在低速和高速行駛下轉向系統(tǒng)的能耗情況。

以上研究對不同工況下車輛轉向系統(tǒng)的能耗進行了很有價值的分析,但并未考慮泵源壓力等油源因素對多軸轉向系統(tǒng)能耗和效率的影響。

針對以上問題,以七軸起重機為對象,筆者通過分析單軸轉向系統(tǒng)動力學模型,建立單軸轉向系統(tǒng)能耗模型,基于單軸轉向系統(tǒng)模型與Ackerman轉向定理,推導出多軸轉向系統(tǒng)的能耗模型,并為轉向系統(tǒng)設計一個能耗測試循環(huán),以分析起重機在行駛工況下多軸轉向系統(tǒng)的能耗特性,通過仿真驗證上述對起重機轉向系統(tǒng)能耗的分析;最后設計一種適用于起重機多軸轉向系統(tǒng)的多級壓力源切換的轉向節(jié)能方案。

1 多軸轉向系統(tǒng)能耗建模

在重型車輛/起重機多軸轉向系統(tǒng)中,由于各轉向軸結構與工作原理一致,且相互獨立互不影響,筆者基于電液助力式轉向系統(tǒng),先通過分析其機械結構和液壓系統(tǒng)的原理,建立單軸轉向系統(tǒng)動力學模型與能耗模型,再根據(jù)Ackerman轉向定理分析各軸轉角關系,聯(lián)立各軸轉向系統(tǒng)能耗模型,便可得到多軸轉向系統(tǒng)能耗模型。

1.1 電液助力轉向系統(tǒng)動力學模型

電液助力轉向系統(tǒng)示意圖如圖1所示。

圖1 電控液壓助力式轉向系統(tǒng)示意圖1—輪胎;2—轉向節(jié);3—伺服比例閥;4—車橋;5—轉向助力缸;6—轉向橫拉桿;7—轉向節(jié)臂

電液助力轉向系統(tǒng)主要是通過檢測轉角信號來控制液壓系統(tǒng),為轉向系統(tǒng)提供壓力和流量,驅動機械機構轉向。其主要工作過程為:

液壓系統(tǒng)接收轉角信號,通過伺服比例閥控制串聯(lián)的雙轉向助力缸的驅動力和速度,驅動轉向梯形機構,再通過轉向節(jié)和輪轂實現(xiàn)轉向。

由于該電液轉向系統(tǒng)模型推導已在之前發(fā)表的論文中進行詳細描述[17],在此筆者不對系統(tǒng)機械模型和液壓模型進行贅述,只給出推導結果。

1.1.1 機械模型

圖1中,右側輪胎繞主銷轉動的轉角為β,左側為α。筆者以右側輪轉角為自變量β,根據(jù)拉格朗日動力學方程,可以得到電液伺服轉向系統(tǒng)中機械部分的動力學方程:

(1)

1.1.2 液壓模型

通過推導,可以獲得電液轉向系統(tǒng)的液壓模型:左右轉向助力缸驅動力、雙轉向助力缸的流量連續(xù)方程和閥口流量方程。

其中,雙轉向助力缸的驅動力可以表示為:

(2)

伺服比例閥的閥口流量方程為:

(3)

雙轉向助力缸的流量連續(xù)性方程為:

(4)

式中:p1,p2—伺服比例閥A、B口的壓力;a,A—轉向助力缸有桿腔與無桿腔的面積;r—助力缸活塞面積比;q1,q2—流入和流出雙轉向助力缸的流量;Cd—閥口的流量系數(shù);w—閥口的面積梯度;xv—閥芯位移;ρ—液壓油的密度;ps—泵源壓力;xL,xR—左、右側轉向助力缸的位移;Cip,Cep—轉向助力缸內泄漏與外泄漏系數(shù);Vt—有桿腔和無桿腔的總容積;βe—有效體積彈性模量。

1.2 單軸轉向系統(tǒng)能耗模型

為研究轉向系統(tǒng)的能耗特性,需要對其能耗情況以及各部分能量損失進行分析。其中,轉向系統(tǒng)的能量損失包括閥口節(jié)流損失、助力缸泄漏損失、助力缸內的摩擦損失、油液壓縮損失等。因此,基于前文所搭建的轉向系統(tǒng)動力學模型,筆者建立轉向系統(tǒng)的總能耗模型及各部分能量損失模型,并對其進行分析。

1.2.1 轉向系統(tǒng)能耗模型

轉向系統(tǒng)能耗也即轉向系統(tǒng)的輸入能量。一般情況下,轉向系統(tǒng)都采用恒壓源進行供能。因此,可以由轉向系統(tǒng)的泵源壓力與流量得到轉向系統(tǒng)的輸入能量:

(5)

式中:Pin—轉向系統(tǒng)輸入功率。

1.2.2 轉向系統(tǒng)閥口節(jié)流損失模型

轉向系統(tǒng)的閥口節(jié)流損失主要是由于流量流經(jīng)閥口時導致壓力損失,進而造成能量損失,閥口節(jié)流損失與閥口間壓差有關。因此,閥口節(jié)流損失可以通過泵源壓力pS,伺服比例閥A、B口壓力(p1和p2),以及系統(tǒng)工作流量(q1和q2)得到。

轉向系統(tǒng)的閥口節(jié)流損失能量為:

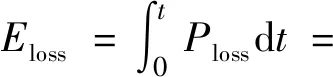
(6)

式中:Ploss—轉向系統(tǒng)閥口節(jié)流損失功率;pT—回油口壓力。

1.2.3 助力缸的泄漏損失模型

助力缸的泄漏可分為從高壓腔向低壓腔的內泄漏,以及液壓缸向系統(tǒng)外部的外泄漏。液壓缸的泄漏會造成系統(tǒng)的能量損失,其損失量與液壓缸的壓力和流量有關。

液壓缸的泄漏流量可表示為:

(7)

(8)

所以助力缸的泄漏損失功率可以表示為:

Pleak=q1leakp1+q2leakp2

(9)

助力缸的泄漏損失能量為:

(10)

1.2.4 助力缸內的摩擦損失模型

液壓助力缸的摩擦損失是由于活塞和油液與液壓缸壁之間的摩擦造成的,與液壓缸的阻尼系數(shù)和活塞的移動速度有關。

因此,可以得到助力缸的摩擦損失功率:

(11)

助力缸的摩擦損失能量為:

(12)

式中:BP—助力缸的阻尼系數(shù)。

1.2.5 油液壓縮損失模型

在助力缸活塞運動時,助力缸內的有桿腔與無桿腔的體積發(fā)生變化,對油液產(chǎn)生壓縮,從而造成系統(tǒng)的容積損失。

因油液壓縮造成的流量變化為:

(13)

油液壓縮損失功率可以表示為:

PC=q1Cp1+q2Cp2

(14)

油液壓縮損失能量為:

(15)

筆者根據(jù)式(5,6,10,12,15),建立轉向系統(tǒng)仿真模型,分析轉向系統(tǒng)能耗及各部分能量損失情況;設定泵源壓力為15 MPa,給右側輪轉角以正弦輸入。

系統(tǒng)的相關參數(shù)如表1所示。

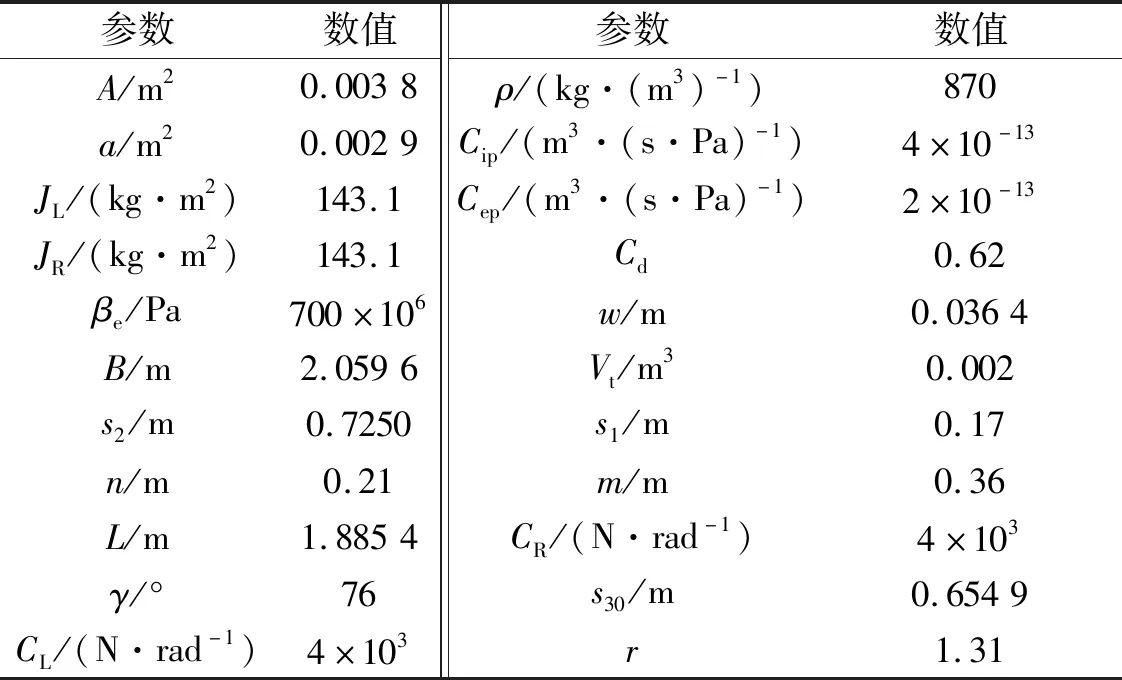
表1 系統(tǒng)的相關參數(shù)值

在上述工況下,通過仿真得到的轉向系統(tǒng)能耗和各部分能量損失的對比情況如圖2所示。

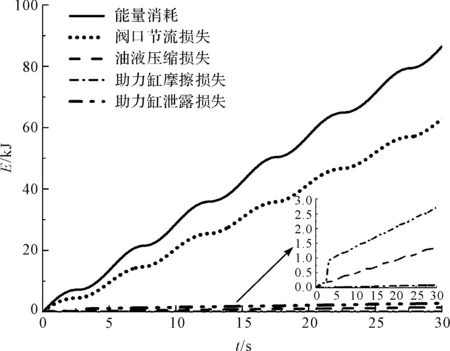
圖2 轉向系統(tǒng)能耗及各部分能量損失對比

通過計算可得,閥口節(jié)流損失約占轉向系統(tǒng)能耗73.3%,助力缸泄漏損失比重約為1.6%,助力缸摩擦損失比重不足1%,油液壓縮損失比重約為1.1%。

由此可見,與閥口節(jié)流損失相比,轉向系統(tǒng)其他部分的損失量很小,可以忽略不計。因此,探索影響轉向系統(tǒng)能耗與效率的主要因素,可忽略次要因素的影響。

1.3 多軸轉向系統(tǒng)能耗模型

在得到單軸轉向系統(tǒng)能耗模型之后,筆者針對車輛行駛的不同工況,分析各軸轉角之間的關系。通過聯(lián)立各軸轉向系統(tǒng)能耗模型,得到多軸轉向系統(tǒng)的能耗模型。

此處以某七軸全地面起重機為例。

一般會根據(jù)車速的不同,起重機選擇不同的轉向模式。常見的轉向模式示意圖如表2所示。

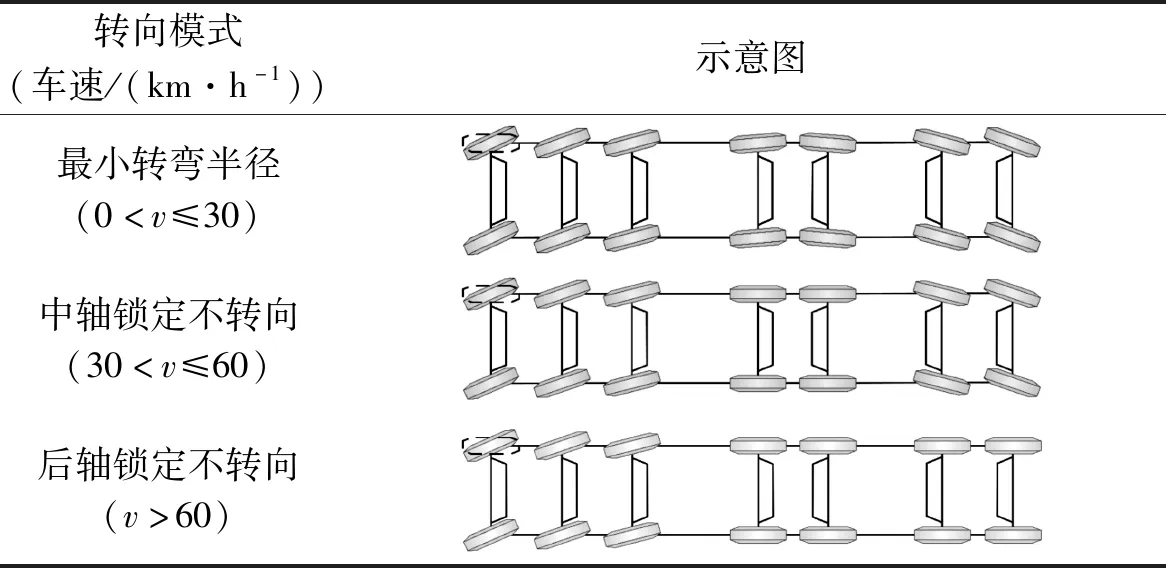
表2 不同轉向模式的示意圖

根據(jù)每種轉向模式的特點,筆者分別對起重機多軸轉向系統(tǒng)能耗模型進行建模。

1.3.1 最小轉彎半徑轉向模式

最小轉彎半徑轉向模式以第1軸右輪轉角為輸入信號,調節(jié)第2軸至第7軸轉向。

根據(jù)參考相關文獻[18],筆者建立七軸全地面起重機的轉向運動二自由度動力學模型,如圖3所示。

圖3 多軸轉向系統(tǒng)二自由度動力學模型

筆者提出以下假設:

(1)忽略車輪滾動阻力、空氣阻力等影響;

(2)忽略懸架的作用;車身只作平行于地面的平面運動,即沿z軸的位移、繞y軸的俯仰角和繞x軸的側傾角均為零;

(3)輪胎工作在線性區(qū),側偏力和側偏角成正比;

(4)忽略轉向盤、轉向器等對轉向系統(tǒng)影響,直接把第一軸右側車輪轉角作為輸入。

車輛受外力沿Y軸合力和繞Z軸轉矩和為:

(16)

式中:M—整車質量;ay—在Y軸方向上車輛質心處的慣性加速度;Fi—第i軸輪胎受到的側偏力;φi—第i軸輪胎側偏角;ki—第i軸的輪胎綜合側偏剛度;βi—第i軸的右側輪的轉角;Iz—整車繞Z軸的轉動慣量;ψ—車輛轉向時的橫擺角,車輛縱軸與坐標系X軸的夾角;Li—質心到第i軸的距離,在質心之前為正,質心之后為負。

其中:

Fi=kiφi

(17)

(18)

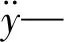
因此,可將多軸轉向系統(tǒng)二自由度動力學模型表示成如下形式:

(19)

設γ為車輛的方向角,則車輛角速度為:

(20)

由此可得車輛的向心加速度:

(21)

設ξi是第i軸車輪的實際速度與X軸的夾角,則有:

(22)

由式(22)可得到輪胎側偏角為:

(23)

根據(jù)Ackerman轉向定理,可以得到各軸與第一軸的轉向角關系:

(24)

式中:li—各軸到瞬心在X軸投影點的距離。

li=Li-Δ

(25)

式中:Δ—質心到瞬心在X軸投影的距離。

采用小轉角近似,可將式(24)簡化為:

(26)

(27)

根據(jù)零質心側偏角,即δ=0,式(27)可得到質心和瞬心之間的距離為:

(28)

將式(28)代入式(26),即可得各軸轉角βi。

1.3.2 中軸鎖定不轉向模式

該轉向模式第四、五軸鎖定不轉向,通過調節(jié)第一、二、三、六、七軸實現(xiàn)車輛的轉向。

設第i軸與第一軸之間的距離為ki(i=2,3,4,5,6,7),L為瞬時中心到右側輪的距離。

由于第四、第五軸鎖定不轉向(β4=β5=0,α4=α5=0),車輛轉向的瞬時中心水平線處于第四軸與第五軸的中間位置,所以可以得到各軸到瞬時中心水平線的距離為:

(29)

根據(jù)Ackerman轉向定理,可得轉向模式二下各轉向軸轉角與第一軸轉角之間的關系:

(30)

1.3.3 后軸鎖定不轉向模式

該轉向模式下后四軸鎖定不轉向,僅通過前三軸實現(xiàn)車輛轉向。

由于后四軸鎖定不轉向(β4=β5=β6=β7=0,α4=α5=α6=α7=0),車輛的瞬時轉向中心水平線處于第五軸與第六軸的中間位置。

該轉向模式二下各軸到瞬時中心水平線的距離為:

(31)

同理,根據(jù)Ackerman轉向定理,可以得到轉向模式三下各軸的轉角關系:

(32)

此處仍以某七軸全地面起重機為參考對象[19，20]。

其整車質量為26 082 kg,各轉向軸的輪胎綜合側偏剛度為350 kN/rad,根據(jù)其實際情況及轉向的參數(shù)作用規(guī)律,選定其轉向參數(shù),各軸到質心的距離:L1=6.15 m,L2=4.5 m,L3=2.85 m,L4=0.15 m,L5=-1.8 m,L6=-4.5 m,L7=-6.15 m。

基于單軸轉向系統(tǒng)能耗模型,并結合上述3種轉向模式下各轉向軸之間的轉角關系,可以建立起重機多軸轉向系統(tǒng)的能耗模型,以進行多軸轉向系統(tǒng)能耗特性的研究。

2 多軸轉向系統(tǒng)能耗仿真分析

為了分析車輛行駛時轉向系統(tǒng)能耗,筆者通過構建包含轉向信息的能耗測試駕駛循環(huán),并在MATLAB/Simulink中建立多軸轉向系統(tǒng)能耗仿真模型,以探索多軸轉向系統(tǒng)能耗的主要影響因素的變化規(guī)律。

2.1 行駛工況下多軸轉向系統(tǒng)能耗仿真建模

車輛行駛的NEDC駕駛循環(huán)如圖4所示。

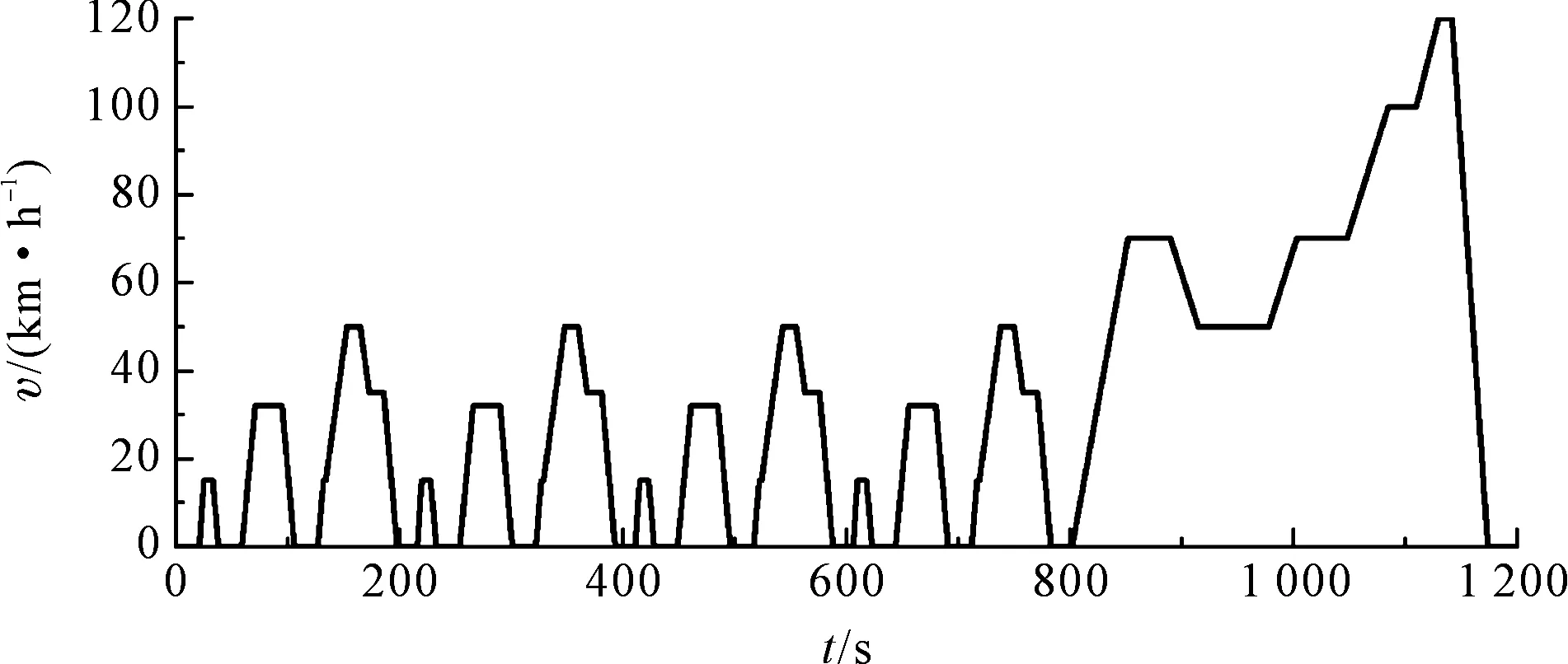
圖4 NEDC駕駛循環(huán)

基于圖4的NEDC駕駛循環(huán),可以分析七軸全地面起重機其多軸轉向系統(tǒng)正常行駛工況下的能耗情況。在仿真分析中,起重機可根據(jù)NEDC駕駛循環(huán)中的車速信息來切換其轉向模式,以模擬實際起重機的行駛轉向情況。

但是NEDC駕駛循環(huán)中僅包含了車速信息,并沒有轉角信號,難以直接用于分析轉向系統(tǒng)能耗。因此,筆者根據(jù)車輛在行駛過程中轉向的特點,設計了與之匹配的轉向角度循環(huán),從而構建一個可用于轉向系統(tǒng)能耗分析的新型駕駛循環(huán)系統(tǒng)。

標準駕駛循環(huán)下第一軸轉角信號如圖5所示。

圖5 標準駕駛循環(huán)下第一軸轉角信號

該轉向信號的轉向時間約占總時間的30%,且最大轉向角度可達20°。同時,考慮到通常駕駛過程會經(jīng)常性地微調方向盤,即產(chǎn)生頻繁的小角度轉向,因此該轉向信號還包含了頻率為0.1 Hz、幅值為2°的小轉角循環(huán)。

為分析起重機行駛過程中的能耗特性,基于多軸轉向系統(tǒng)能耗模型與能耗測試駕駛循環(huán),筆者通過MATLAB/Simulink建立了多軸轉向系統(tǒng)能耗仿真模型,如圖6所示。

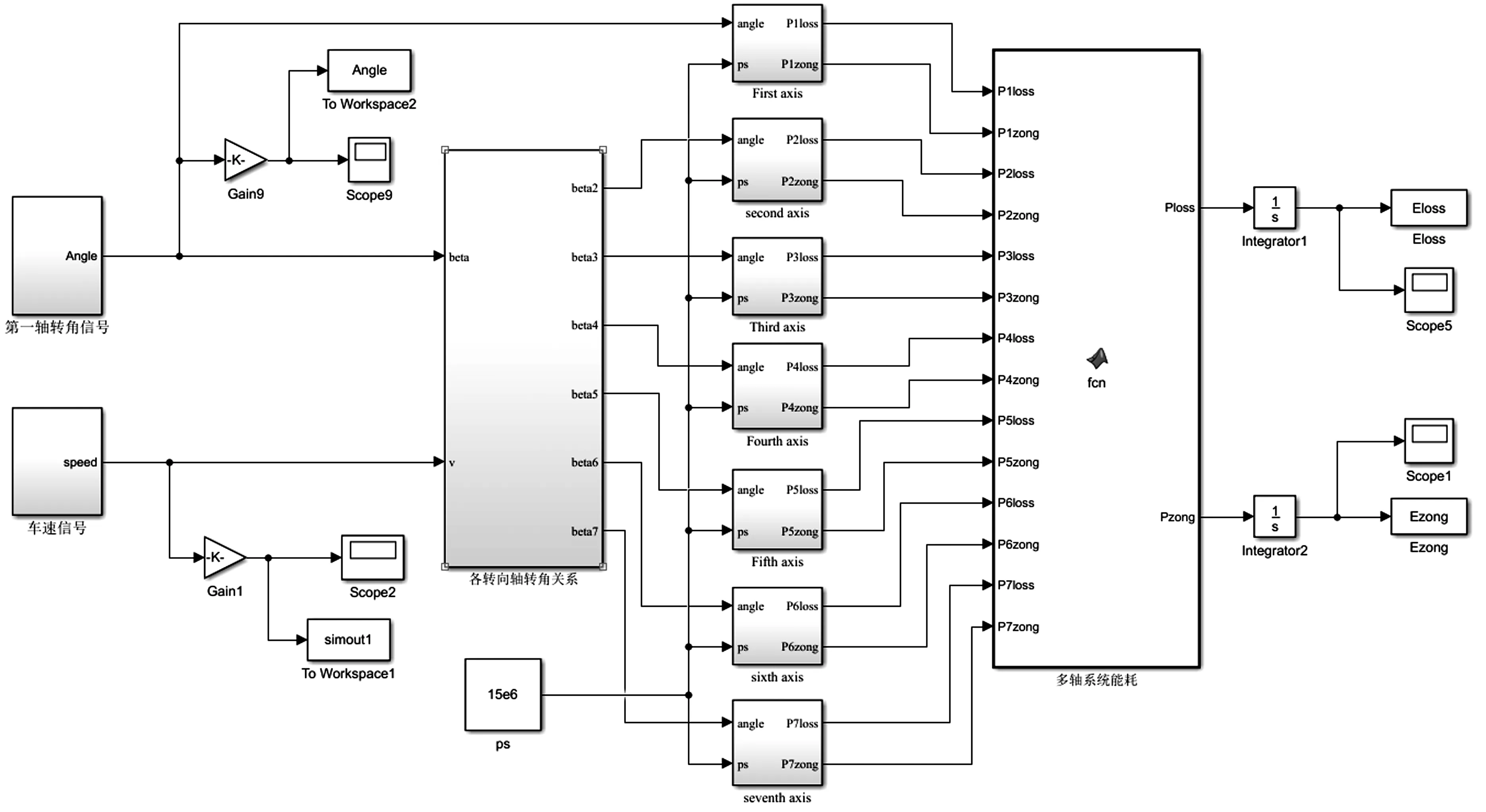
圖6 多軸轉向系統(tǒng)能耗Simulink仿真模型

該模型包含輸入信號、各轉向軸轉角關系、單軸轉向系統(tǒng)能耗部分以及七軸轉向系統(tǒng)能耗累加部分,其中輸入信號部分由第一軸轉角信號和車速信號組成。

在多軸轉向系統(tǒng)能耗的研究中,需得到輪胎轉向阻力矩,而目前并沒有行駛工況下的轉向阻力矩模型。由于轉向阻力矩與車速有著密切關系,且隨車速的提高而變小。因此,可將原地轉向阻力矩作為參考,假定起重機在低速行駛時的轉向阻力矩與原地轉向阻力矩相同,中速行駛時轉向阻力矩為其1/2,高速行駛時的轉向阻力矩為其1/4。

筆者應用PACEJKA H[21]提出原地轉向阻力矩的數(shù)學模型,如圖7所示。

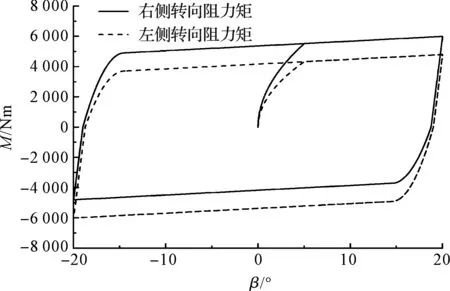
圖7 轉向系統(tǒng)原地轉向阻力矩

2.2 多軸轉向系統(tǒng)能耗影響因素分析

筆者以圖4與圖5組成的新型標準循環(huán)為多軸轉向系統(tǒng)的輸入信號,以圖6的阻力矩模型模擬起重機在行駛過程中,低、中、高速時的轉向阻力矩,對多軸轉向系統(tǒng)能耗的影響因素進行分析。

2.2.1 泵源壓力對能耗的影響

由前文對單軸轉向系統(tǒng)各部分能量損失的分析可知,泵源壓力是影響轉向系統(tǒng)能耗的主要因素。為探究泵源壓力對多軸轉向系統(tǒng)的能量損耗和效率的影響規(guī)律,要在不同泵源壓力下,對多軸轉向系統(tǒng)的能量損耗情況進行分析。

筆者設定泵源壓力為20 MPa、17.5 MPa、15 MPa、12.5 MPa和10 MPa,以上述七軸起重機為研究對象(系統(tǒng)其他參數(shù)的設置如表1所示),通過仿真得知不同泵源壓力下多軸轉向系統(tǒng)能耗情況。

不同泵源壓力下,多軸轉向系統(tǒng)能耗和能量損失如圖8所示。

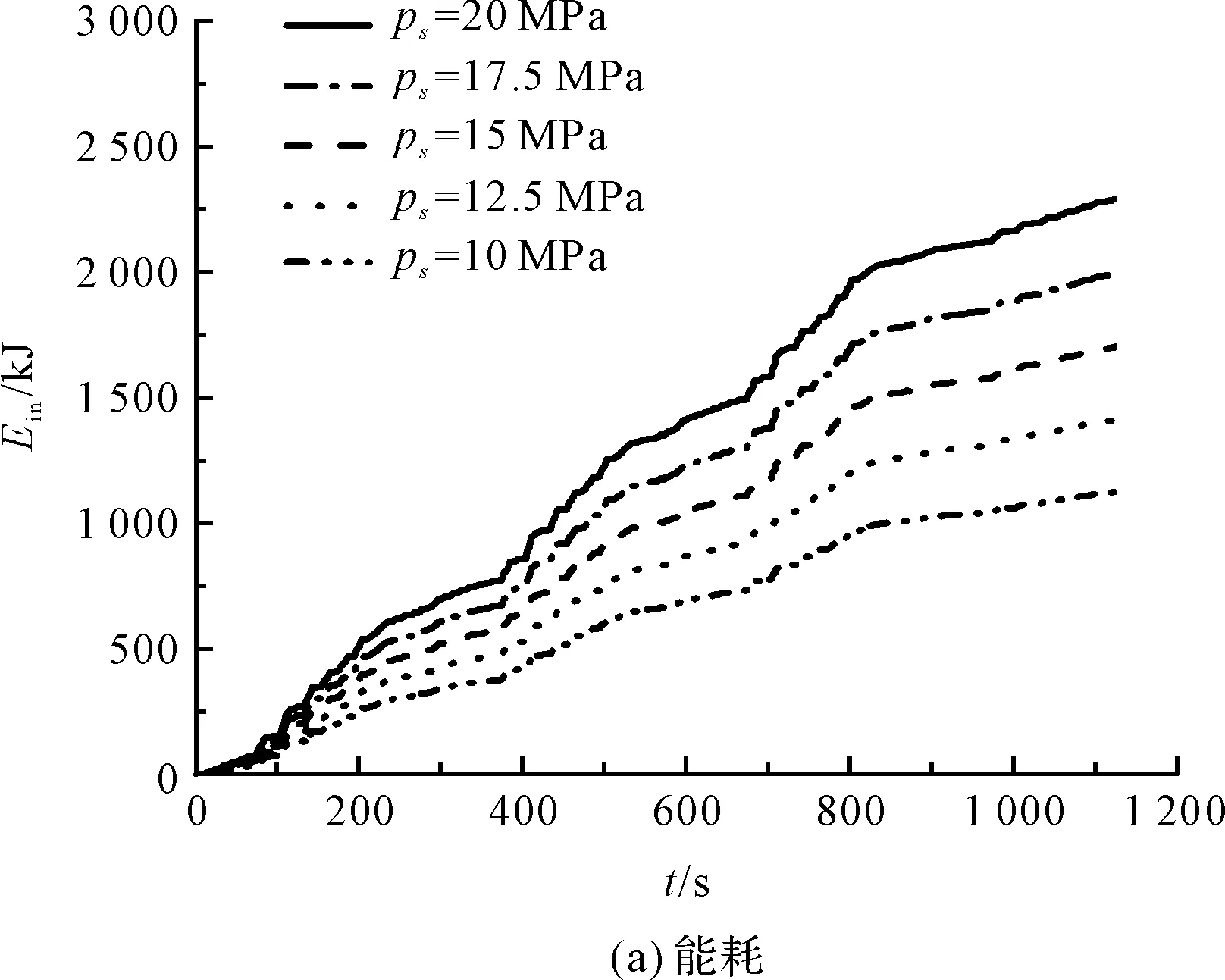
圖8 不同泵源壓力下多軸轉向系統(tǒng)能耗與能量損失

能耗與能量損失的數(shù)據(jù)對比如表3所示。

表3 不同泵源壓力下轉向系統(tǒng)能耗情況

由仿真結果可知:當泵源壓力以2.5 MPa的差值從20 MPa遞減至10 MPa時,轉向系統(tǒng)的能量消耗和能量損失也都以約300 kJ的差值遞減。這是由于在相同的負載工況下,系統(tǒng)為克服負載所需要的能量是一定的,所以在不同泵源壓力下,轉向系統(tǒng)總能量消耗與能量損失的差值也即系統(tǒng)的有用功基本相同。但由于做的有用功是一樣的,多軸轉向系統(tǒng)平均效率的降低卻是呈現(xiàn)非線性變化關系。

由表3可知：降低泵源壓力可以減少行駛時多軸轉向系統(tǒng)的能耗和能量損失,提高平均效率,且選擇越小的泵源壓力,其平均效率提升程度將愈發(fā)明顯。因此,為減少多軸車輛轉向系統(tǒng)的能耗,可通過設計一套新的節(jié)能方案,使轉向系統(tǒng)泵源壓力適應負載的變化,從而達到節(jié)能的目的。

但泵源壓力不僅對系統(tǒng)的能耗特性有重要影響,同時還影響著系統(tǒng)的動態(tài)控制性能。而筆者著重分析的是多軸轉向系統(tǒng)的能耗,因此,兼顧能耗與動態(tài)控制性能將是下一步研究的重點。

2.2.2 轉向模式對能耗的影響

起重機在不同轉向模式下行駛時,由于車速的不同,轉向阻力矩也存在顯著差異。通過圖6得到的原地轉向阻力矩模型,可以模擬低、中、高速3種不同工況下的轉向阻力矩。

筆者設定泵源壓力為15 MPa,以上述七軸起重機為研究對象(系統(tǒng)其他參數(shù)的設置如表1所示),以圖5第一軸轉角信號作為輸入信號,通過仿真分析得到不同轉向模式下轉向系統(tǒng)的能耗情況。

不同轉向模式下,多軸轉向系統(tǒng)能耗和能量損失圖如圖9所示。

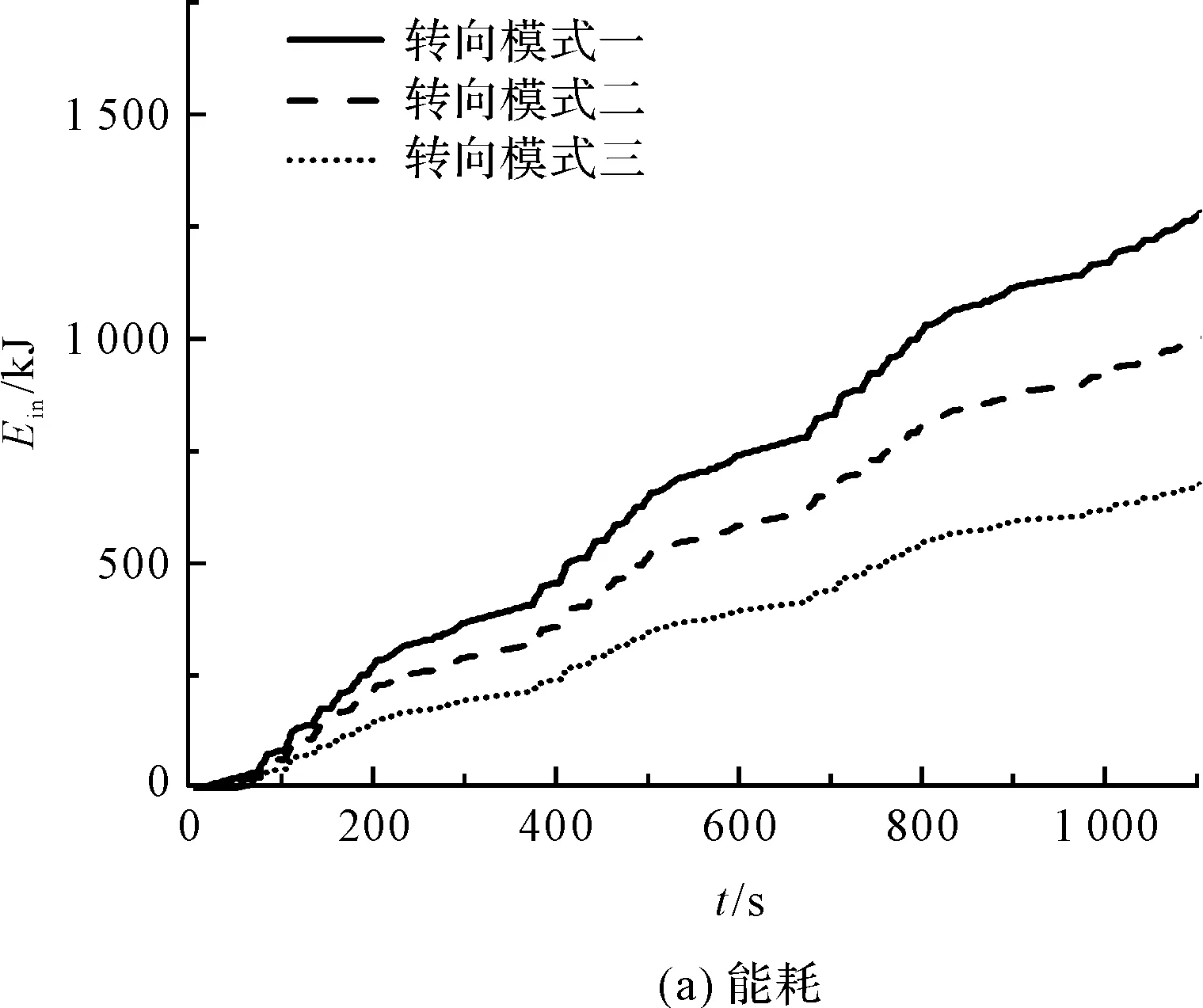
圖9 不同轉向模式下多軸轉向系統(tǒng)能耗與能量損失

圖9中,3種轉向模式分別對應起重機低速、中速和高速的轉向行駛模式。

3種工況下,轉向系統(tǒng)能耗和能量損失對比如表4所示。

表4 3種工況下轉向系統(tǒng)能耗情況

由表4可知,3種轉向模式的平均效率分別為28%、23%和13%。起重機在低速行駛時多軸轉向系統(tǒng)的平均效率最大,這是由于低速時的轉向阻力矩比中高速時的大,在相同泵源壓力下系統(tǒng)對負載做了更多的有用功;隨著車速的增加,轉向阻力矩逐漸減小,為克服負載所做的有用功隨著減小,則平均效率逐漸減低。

因此,在滿足車輛負載需求和行駛靈活性的情況下,可以通過設計不同的轉向模式以匹配不同的行駛工況,進而減少行駛時轉向系統(tǒng)的能耗。

3 多軸轉向系統(tǒng)多級壓力源節(jié)能研究

在重型車輛實際行駛過程中,各軸間的轉向負載因轉向模式以及轉向角度的不同存在著差異,所以當系統(tǒng)由高轉向負載切換至低轉向負載工況,或轉向模式切換成部分軸鎖定不轉向的模式時,恒壓式供油方式將造成大量的輸入能量浪費。

針對這一核心問題,筆者提出了一種多級壓力源的轉向方案,各軸可以隨負載和轉向模式的變化進行分級調壓。

3.1 多級壓力源系統(tǒng)工作原理

基于“STEAM”系統(tǒng)[22],筆者設計了起重機多軸轉向系統(tǒng)的多級壓力源的節(jié)能系統(tǒng)。該系統(tǒng)通過轉向泵、蓄能器和閥矩陣等組成多條壓力支路,多級壓力源系統(tǒng)液壓原理圖如圖10所示。

圖10 多級壓力源多軸轉向系統(tǒng)液壓原理圖1—內燃機;2—動力泵;3—單向閥;4—電磁卸荷閥;5—高壓蓄能器;6—中壓蓄能器;7—二位二通伺服比例閥;8—開關閥矩陣;9—電磁開關閥;10—馬達;11—輔助泵

該多級壓力源切換系統(tǒng)包括3條壓力支路,為高壓支路(high pressure,HP)、中壓支路(medium pressure,MP)和零壓支路(tank pressure,TP),壓力支路由轉向泵、蓄能器、單向閥、電磁卸荷閥、閥矩陣組成。

為保證系統(tǒng)有足夠的驅動能力,每條壓力支路的壓力選取應滿足該支路驅動的最大轉向負載時的壓力要求。壓力支路主要是通過蓄能器來保持系統(tǒng)的壓力,動力泵為蓄能器補充油液、提供能量,并且單向閥3—1將動力泵與蓄能器隔開,防止油液反向流回動力泵。而在轉向系統(tǒng)工作時主要有兩條壓力支路,系統(tǒng)通過開關閥矩陣8來選擇驅動負載的壓力支路。當開關閥矩陣中的8—1、8—7、8—13號開關閥處于開啟狀態(tài)則系統(tǒng)切換至高壓支路,動力泵2提供的能量通過由同軸串聯(lián)的馬達10與輔助泵11為核心元件組成的變壓單元,為高壓蓄能器5補充油液,此時電磁開關閥處于關閉狀態(tài);當開關閥矩陣中的8—2、8—8、8—14號開關閥開啟,系統(tǒng)切換中壓支路,動力泵2為中壓蓄能器6補充油液。

由開關閥組成的閥矩陣如圖11所示。

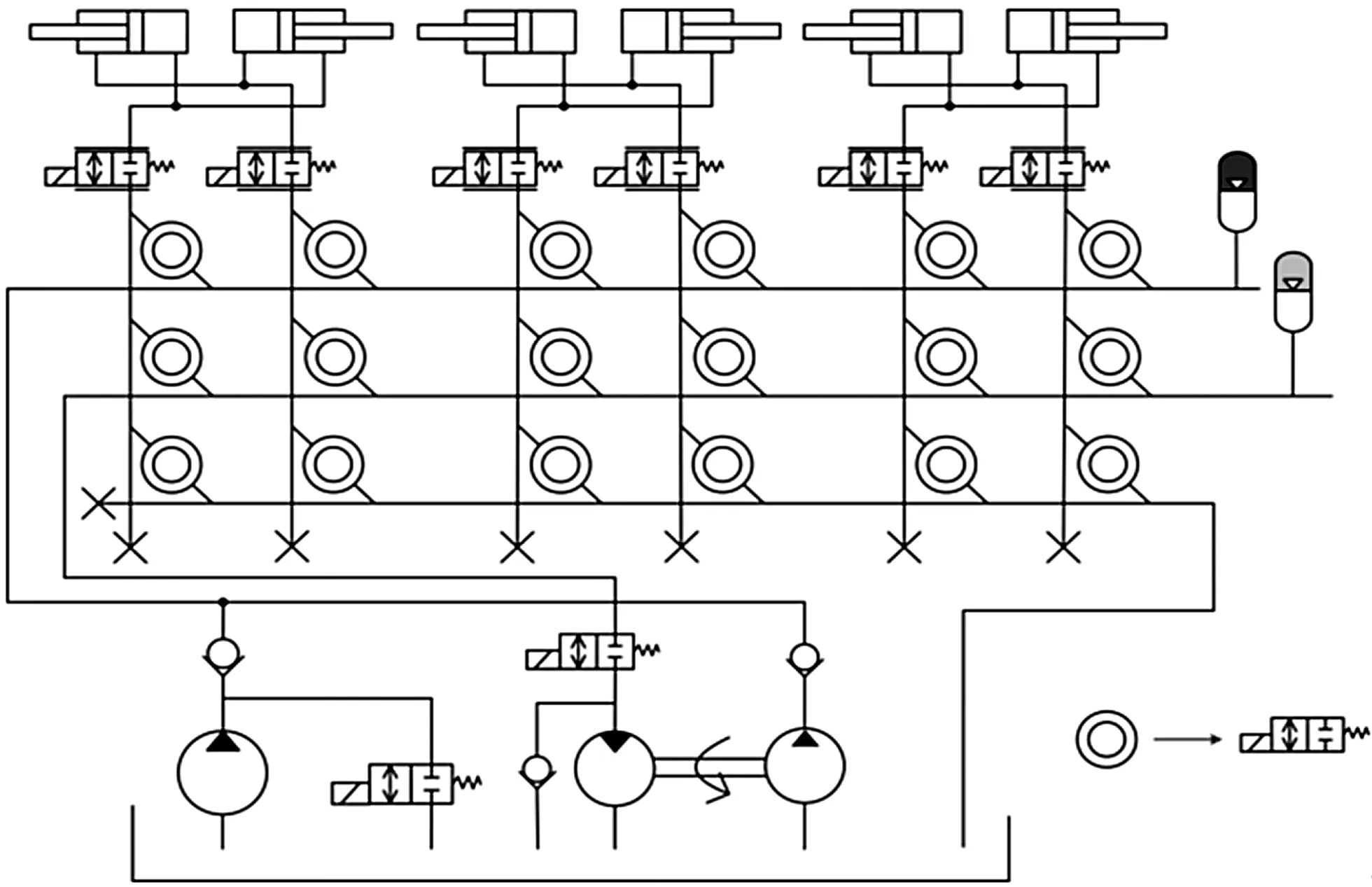
圖11 多級壓力源系統(tǒng)開關閥矩陣示意圖

動力泵在工作過程中有兩種工作狀態(tài),分別為供能和卸荷狀態(tài),主要通過控制泵出口處電磁卸荷閥4的通斷來切換動力泵的工作狀態(tài)。轉向系統(tǒng)工作時,通過蓄能器保持壓力支路中的壓力,此時需要動力泵向壓力支路中的蓄能器補充油液,此時動力泵處于供能狀態(tài)。當壓力支路中的蓄能器達到設定的壓力值,電磁卸荷閥開啟,動力泵處于卸荷狀態(tài),由蓄能器維持壓力支路的壓力。

由于蓄能器在工作時不斷向壓力支路輸出油液會使蓄能器內的壓力下降,需要動力泵對其進行油液補充。為避免頻繁切換動力泵的工作狀態(tài),并保證壓力支路中能正常驅動轉向軸,可設定壓力支路的壓力閾值:壓力支路的壓力值小于設定值與壓力閾值差值,則動力泵處于供能狀態(tài);當壓力支路中的壓力值大于設定值與壓力閾值和值,電磁卸荷閥開啟,動力泵為卸荷狀態(tài)。

該多級壓力源轉向系統(tǒng)具有多條壓力支路,而工作時壓力支路是根據(jù)轉向系統(tǒng)的轉向負載范圍來選擇的,不同轉向負載范圍匹配不同的壓力支路,以提高系統(tǒng)輸入能量與負載的匹配性。

當轉向系統(tǒng)處于高轉向負載工況時,通過控制由開關閥組成的閥矩陣的狀態(tài)來實現(xiàn)高壓支路的切換,經(jīng)伺服比例閥驅動轉向助力缸從而實現(xiàn)車輛轉向;而當轉向負載較小時,則通過閥矩陣控制中壓支路接入系統(tǒng)實現(xiàn)轉向。

3.2 多級壓力源系統(tǒng)壓力組合

轉向助力缸在驅動車輪轉向時,轉向負載方向與助力缸的方向相反,根據(jù)轉向負載選擇不同的壓力支路,因此,其進口壓力p1與出口壓力p2有9種不同的壓力組合。

各種壓力組合對應了轉向系統(tǒng)的不同工況,其工況可分為:非轉向工況、左轉向工況以及右轉向工況。其中,非轉向工況的壓力組合為零壓-零壓(tank-tank,T-T)、中壓-中壓(medium- medium,M-M)、高壓-高壓(high-high,H-H)3種壓力組合;左轉向工況的壓力組合為中壓-零壓(medium-tank,M-T)、高壓-零壓(high-tank,H-T)、高壓-中壓(high-medium,H-M)3種壓力組合;右轉向工況的壓力組合為零壓-中壓(tank-medium,T-M)、零壓-高壓(tank-high,T-H)、中壓-高壓(medium-high,M-H)3種壓力組合。

多級壓力源系統(tǒng)下,轉向系統(tǒng)的工作狀態(tài)如圖12所示。

圖12 多級壓力源系統(tǒng)下轉向系統(tǒng)的工作狀態(tài)

多級壓力源系統(tǒng)轉向工況中,不同壓力組合的選擇也是根據(jù)轉向系統(tǒng)的轉向工況和轉向模式:在轉向負載高的工況下,左轉向選擇H-T壓力組合,右轉向選擇T-H壓力組合;在轉向負載較低的工況下,左轉向選擇M-T壓力組合,右轉向選擇T-M壓力組合。

其中,H-T、M-T、T-M、T-H這4種轉向組合又為轉向系統(tǒng)的普通模式,多級壓力源系統(tǒng)中的特點為單條壓力支路的能量消耗。當轉向系統(tǒng)選擇H-M和M-H的壓力組合時,多級壓力源系統(tǒng)處于能量再生模式,一條壓力支路為能量消耗模式,另一條壓力支路為能量回收模式。該模式適用于路面等級變化頻繁且轉向負載變化廣的工況。

當重型車輛行駛于公路路面時,轉向負載的變化主要與車輛的行駛速度有關,低速行駛時轉向負載大,隨著車速的提高,轉向負載也隨之增大。因此,在公路行駛工況下,多級壓力源主要采用普通模式進行工作。在低車速行駛時,選擇H-T與T-H壓力組合;在中、高速行駛時,選擇M-T與T-M壓力組合。

而在路面等級變化頻繁、負載范圍變化廣的工況,多級壓力源系統(tǒng)應采用能量再生模式,既能通過高壓支路提供足夠的驅動力,又可以通過中壓支路回收多余的能量。

該多級壓力源系統(tǒng)具有多條不同壓力設定值的壓力支路,各壓力支路根據(jù)轉向負載的區(qū)間,設定不同的泵源壓力值來匹配多執(zhí)行器的工況要求,在大轉向負載工況時切換至高壓支路,實現(xiàn)強驅動能力;在轉向負載較小時,可切換至中壓力支路,從而可以實現(xiàn)多軸轉向系統(tǒng)的節(jié)能。

4 結束語

七軸全地面起重機電液助力轉向系統(tǒng)存在能耗高的問題,為此,在考慮了油源因素對多軸轉向系統(tǒng)能耗和效率影響的基礎上,筆者對起重機多軸轉向系統(tǒng)的能耗特性進行了研究。

筆者以七軸全地面起重機多軸轉向系統(tǒng)為研究對象,分析了各種行駛工況下多軸轉向系統(tǒng)的能耗特性,并對其進行了仿真分析,最后提出了一種多級壓力源的轉向方案。

研究結論如下:

(1)通過對電液伺服轉向系統(tǒng)進行動力學分析,建立了單軸轉向系統(tǒng)能耗模型。通過分析可知,在轉向系統(tǒng)能量損失的幾個部分中,閥口節(jié)流損失是影響最大的因素,因此在分析轉向系統(tǒng)能耗時,可忽略其他次要的因素;

(2)設計了一個與NEDC駕駛循環(huán)相匹配的轉角循環(huán),進而可用于分析行駛工況下多軸轉向系統(tǒng)的能耗;并基于Ackerman轉向原理得到各軸轉角關系,聯(lián)立各軸轉向系統(tǒng)能耗模型，得到行駛工況下的多軸轉向系統(tǒng)能耗模型;分析了影響多軸轉向系統(tǒng)能耗的兩個因素(泵源壓力和轉向模式)，可以得出結論，即降低泵源壓力可以降低車輛行駛時多軸轉向系統(tǒng)的能耗,提高平均效率,且泵源壓力越小,平均效率提升越明顯;起重機在低速行駛時多軸轉向系統(tǒng)的平均效率最大,其轉向阻力矩隨車速變化而變化,車速越低轉向阻力矩越大,則系統(tǒng)對負載的做功越多,平均效率越高;

(3)提出了一種可進行壓力源切換的多級壓力源節(jié)能系統(tǒng),各軸可實現(xiàn)隨負載和轉向模式的變化進行分級調壓,從而可以實現(xiàn)多軸轉向系統(tǒng)的節(jié)能。

在接下來的工作當中,筆者將針對設計的多級壓力源節(jié)能方案進行深入的分析,并通過實驗對此進行驗證。