高三數學課堂高效習題設計的探討

◎龍貴妍 （佛山南海西樵高級中學，廣東 佛山 528000）

一、前 言

1.新課標對高三學生的數學素養能力要求提高了.

學科核心素養，是此次高中改革提出的核心概念之一，是指學生在相應課程的學習之后，應達成的正確的價值觀、必備的品格和關鍵能力.數學核心素養包括以下方面：數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析.這些數學的核心素養的培養對高三學生來說就是在數學中解決問題能力的培養.

2.高三數學的復習課需要設計高效的課堂習題.

習題訓練是高三數學課堂的重要活動之一，是學生復習數學知識、鞏固數學知識、培養數學思維能力和提升數學解題能力的必要手段.但是，當前許多習題訓練都采用題海戰術，把相類似的題目收集來就給學生做，造成學生負擔大、效率低，從而降低學生學習數學的興趣.另一方面，學生只會模仿練習，知識遷移的能力弱，換一個說法就是完全不懂題意，或換一個背景就不會分析題目，不利于學生數學思維能力的培養和解決問題能力的培養.

3.高三數學課堂高效習題設計的原則.

高三數學課堂中的有效教學，主要是指教師在課堂教學中遵循數學教學活動的客觀規律，采用適當的教學形式，面向全體學生，投入盡可能少的時間、精力和物力以達成數學教學目標和滿足學生發展需求的教學.筆者認為，高三數學習題的設計須遵守一些原則，比如，以學生的原有知識為基礎設計學生能夠接受的難度的習題，設計的習題要有梯度，等等.

二、設計高效的高三數學課堂習題

1.通過習題重現數學概念，幫助學生理解概念.

2.高三數學復習課堂習題的設計要有梯度.

課堂習題的設計要有梯度，要循序漸進，讓學生的思維發展經歷一個由淺入深的過程，從而完善知識結構.例如，在復習函數的導數應用之單調性的其中一種題型時，針對利用構造函數法解不等式、比較大小等問題，筆者設計了以下題目：

解析 令（）＝（）-，則′（）＝′（）-2.∈［0，＋∞）時，′（）＝′（）-2＞0，所以（）在［0，＋∞）上是增函數.（-）＝（-）-（-）＝（）-＝（），所以（）為偶函數，（）在（-∞，0）上是減函數.因為（-2）-（）≥4-4，所以（-2）-4＋4-≥（）-，所以（-2）-（-2）2≥（）-，即（-2）≥（），所以｜-2 ｜≥｜｜，所以≤1.故選A.

題目3 （2019南昌市摸底調研）已知函數（）是定義在R 上的偶函數，設函數（）的導函數為′（），若對任意＞0 都有2（）＋′（）＞0成立，則（ ）.

A.4（-2）＜9（3）B.4（-2）＞9（3）

C.2（3）＞3（-2）D.3（-3）＜2（-2）

解析 根據題意，令（）＝（），其導數′（）＝2（）＋′（），又對任意＞0 都有2（）＋′（）＞0 成立，則當＞0 時，有′（）＝（2（）＋′（））＞0 恒成立，即函數（）在（0，＋∞）上為增函數.又由函數（）是定義在R上的偶函數，則（-）＝（），則有（-）＝（-）2（-）＝（）＝（），即函數（）也為偶函數，則有（-2）＝（2），且（2）＜（3），則有（-2）＜（3），即有4（-2）＜9（3）.故選A.

上面三個題目的畫線式子都提示了構造一個新的函數來解決問題，但是構造的函數的難度是從淺到深的，給學生一種從看不懂題目到能夠自己做出來的過程，使學生經歷了把知識內化并能應用的過程.通過有梯度的題目設計，學生能順利地掌握知識.

3.課堂習題的設計要體現數學素養的培養.

數學的教學要以培養學生的數學素養為目的，高三的數學復習課堂也不例外.在高三復習時，課堂習題的設計要體現出對學生數學素養的培養，因此我們在選題的時候，要針對每個素養能力的培養有側重地選擇.例如，在培養空間想象能力時，可以選擇立體幾何的題目，減少對計算的要求.在培養學生的計算能力時，可以選擇一些解方程或解析幾何的題目進行訓練.

4.高中數學課堂習題的設計注重對解決數學問題的能力的培養.

教師在設計課堂習題的時候也要顧及學生的心理狀況.比如，學生一直都很害怕長題目，一看就不愿意去做，越是這樣，教師就越不能遷就，要鼓勵學生去分析問題，尋找解決問題的辦法.例如，在講授函數的應用題的時候，教學生如何審題，筆者采用了一道長題目進行分析.

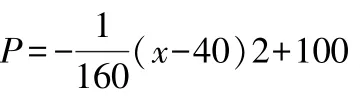
學生剛開始看到題目的時候，基本上不愿意動筆，覺得太長.筆者鼓勵他們嘗試審題，舍掉沒有用的背景文字，找出核心內容，很快，學生從害怕題目，到后來能輕松解決問題，感受到了成功的喜悅.

5.設計習題要符合學生的心理特點，能激發學生的成就感.

高中數學課堂習題的設計還要注意學生的心理特點，開展小競賽的方式能調節課堂氛圍，激發學生的成就感和做數學題目的信心.設計一些開放性的題目讓學生去思考，引導學生多角度、多方面思考問題，培養學生的數學思維能力和創造力.

6.新課標下，多選題要根據高考要求進行設計.

從2021 屆開始，數學高考增加了多選題這一題型.筆者覺得這種題型雖然是新題型，但本質上并不“新”，“正確選項有哪些”這類的舊題其實就是多選題，所以教師在思想上給學生多一點鼓勵，讓學生不怕這種新題型.例如，（2020·山東多選題）已知曲線：＋＝1，則以下正確的是（ ）.

三、注重學生習題訓練形式的設計

（一）習題訓練形式的設計在使用中存在的問題

1.習題訓練形式設計機械化.有些教師直接在題庫中把以往的題目復制粘貼過來，給學生進行機械的課堂練習，忽略了課堂實際和學生的接受能力，既占用了課堂時間，也沒有發揮課堂練習的效果.

2.習題設計形式、方法單一.課堂練習往往是給時間讓學生動手運算，然后老師評講，這種形式過于單一，練習缺乏層次性和開放性，不能滿足不同層次學生的需求，極大束縛了學生思維能力的發展.

3.習題設計形式“一刀切”，沒有關注學生的差異.每個學生的學習基礎、接受能力都不同，同樣的練習肯定會有人“吃不飽”，有人“吃不了”，所以課堂練習要關注學生的差異，力求滿足每個學生的需求.

（二）習題形式設計和篩選要具有反思性

（三）習題形式的設計和篩選要具有層次性

高三數學課堂練習要考慮到練習的難度和層次必須適合不同學生的現有水平，充分考慮學生的不同需求，為所有學生發展提供幫助，為學生的不同發展提供較大的選擇空間.因此課堂練習的設置應由易到難進行安排，使課堂的練習既可以讓學生體驗成功，培養學生學習興趣和信心，又不至于因練習太易或太難而使學生失去認真練習的動力.

例如，筆者帶領學生復習函數的基本性質，利用定義證明函數的單調性時，同學們都清楚步驟：設元→作差→變形→判號→定論，但是往往在變形這一步中不會因式分解，導致判號亂下結論，于是為了訓練學生用定義證明函數的單調性，筆者給出了以下練習.

練習1：證明函數（）＝-2＋1 在R 上是減函數.

練習2：證明函數（）＝-＋2＋3 在（-∞，1）是增函數.

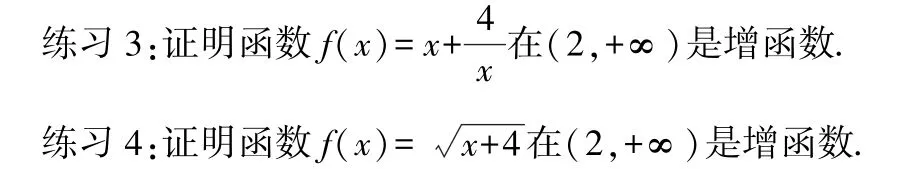
上面的練習設計是從簡單的一次函數到二次函數，再到分式函數，最后是根式函數，層層深入，攻破難點，力爭滿足每個學生的不同學習需求，照顧學生的發展水平.

（四）習題形式的設計要具有對比性

在高三數學課堂教學數學概念的時候，筆者發現學生很容易張冠李戴，分不清楚問題的類型.針對這樣的情況，筆者常用對比性的習題讓學生分析，自己尋找規律，這對于學生理解概念有事半功倍的效果.例如，在學習求解切線方程時，學生會遇到在某點處的切線方程和過某點的切線方程兩個問題，學生容易理解第一個問題，卻經常搞錯第二個問題.針對這一情況，筆者設計了3 個習題給學生練習：

已知曲線（）＝3-，求曲線在點(1，2)處的切線方程.

已知曲線（）＝3-，求曲線過點(1，1) 的切線方程.

已知曲線（）＝3-，求曲線過點(2，-2)的切線方程.

學生分別對三個練習進行分析、計算，發現其中的不同點.對于練習（3），很多學生錯解為點在曲線（）＝3上，然后對函數進行求導，得（）＝3-3，再代入′（2）＝-9，得到所求切線方程為＋2 ＝-9（-2），即9＋-16＝0.但曲線過點的切線與曲線在點處的切線不同，前者既包括點處的切線，也包括過點但切點為另一點的切線，解題時必須理清思路，弄清題意.該題的正確答案為當切點為 (-1，-2)，又過點 (2，-2)時，切線方程為＝-2，當切點為(2，-2)時，切線方程為9＋-16 ＝0.很多學生容易忽略＝-2 這個答案而導致出錯.通過這樣的練習，學生對在某點處的切線方程和過某點的切線方程有了更深層次的理解，學生再犯錯的概率也會降低很多.

學生在進行習題訓練的時候形式要多樣，一節課都是同一個形式的練習，學生會覺得比較悶，很自然會開小差.比如，不需要大量計算的簡單題，可以以搶答、口答的形式完成；圖形題目可以讓一個學生上黑板講，其他學生聽，分析其中的正誤；計算類型的題目可以讓學生從頭到尾自己進行演算，培養學生的運算能力.

結 語

總之，數學習題作為高三復習的主要工具和手段，應設計并利用好，最大程度上提高高三復習的效率.數學題目既要用得恰當，又避免題海戰術，更要培養學生的核心數學思維能力，適應新高考和新課標的要求，這些一直是我們研究和努力的方向.