實現初中數學試卷講評課高效的對策思考

摘要：在新課程新理念下，追求課堂高效是教師的向往;在雙減政策下，更是時代對教師提升教學效能的呼喚。試卷講評課是初中數學教學的重要組成部分，是針對學生考試所反映出的錯誤進行矯正，是對缺漏和不足進行有效的干預，上好講評課對夯實學生雙基、矯正思維障礙、提升分析問題解決問題能力、培養學生創新意識等都有著特殊的意義。

關鍵詞：合理定位;共性錯誤;思維能力

中圖分類號：G633.6文獻標識碼：A文章編號：1673-8918（2022）24-0078-04

目前不少初中數學試卷講評課存在低效或收獲甚微的狀態，比如，教師不顧主次，逐題講解，眉毛胡子一把抓;沒有合理歸類，盲目重復操作，浪費學生的時間;重解題過程，輕方法指導，學生知其然而不知其所以然;面面俱到，一言堂，一講到底，學生缺乏參與，老師講得口干舌燥，學生聽得昏昏欲睡;諸如此類，錯失對學生學習品質提升的機會，嚴重挫敗學生學習數學的熱情，降低課堂實效。初中數學常見的試卷講評課如何追求高效呢？仁者見仁，智者見智，筆者根據多年初中數學試卷講評課的心得體悟，提出幾點思考，以拋磚引玉。

一、 分析有效數據，合理定位，確定教學目標

優質的講評課，備課是個龐大的工程。前期關注考場狀態、成績真實性，及時閱卷統分，進行本班橫向和年段縱向比較，知曉本班這次考試成績的整體情況，清楚各分數段人數的分布，細化到每題得分率（若統考可以利用好分數平臺功能，查閱各種詳細數據，發現學生薄弱環節，非常方便有效），包括典型的錯誤、思維障礙、奇思妙想等。針對試卷暴露出的問題，結合班情、學情，合理定位學生基礎知識、基本技能和學習能力的情況，預測通過師生努力可以達到的水平，制定教學目標，使講評重點突出，有效解決學生最突出、最主要、最想知道的問題，為后續的學習打下知識基礎和提供能力保障。

以下是筆者送教下鄉初三某班的一次試卷講評課的案例。考試卷是《2020年漳州質檢卷》。該試卷關注學生發展，突出能力，能有效區分學生的水平。如第8、11、14、23的第1小題等立足于考查學生對概念的理解和應用;第2、6、21題通過視圖的觀察、平移、旋轉等幾何變換對學生的空間觀念進行考查;第13、19、22、24等題重點考查了高中必備的運算和推理能力;第7、22、23題通過創設與學生生活相關聯的情景，考查學生的應用意識;第25題通過創新題型考查學生的創新意識。

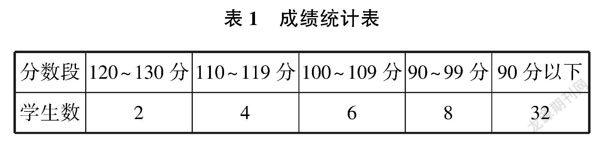
（一）成績統計（見表1）

閱卷之后，跟該班數學任課老師進行了充分溝通，該校處城鄉接合處，“留守學生”多，在高年級留守學生學習上兩極分化現象尤其突出，部分學生有“讀書無用論”的思想，學習上放棄了對自己的要求，基礎薄弱，不思進取，思維欠缺，有16人屬于這種狀況，只做一點填空和選擇題，分數在30分左右，3人有想讀一點數學，無奈綜合因素導致數學學習困難重重，這次測試成績在50分之下。鑒于學生的實際情況和即將面臨中考，針對這19名學生實施分層教學分層布置作業，課堂上特地設計一份數學托底訓練練習，反復訓練最基礎的知識、最基本的技能，課后安排小老師一對一輔導，以達到數學課程要求——人人都能獲得必需的數學，不同的人在數學上得到不同的發展。余下33位學生最低分64分，針對這33位學生的卷面完成情況，分析有效數據，合理定位，確定教學目標。

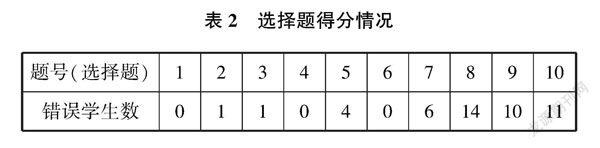
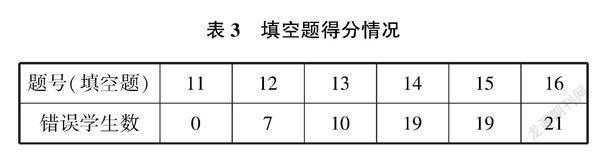
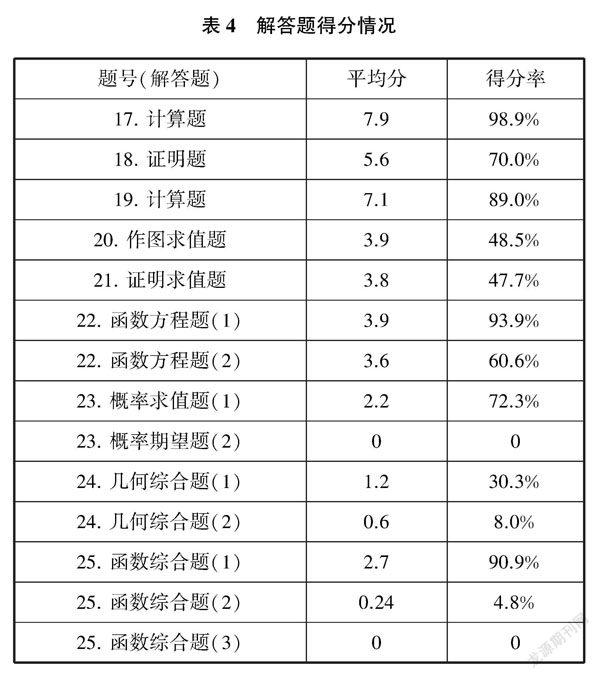
（二）試卷中各題得分情況（參與學生33人，見表2～表4）

分析表2～表4的有效數據統計，教學目標是托底和培優兩頭兼顧，合理定位，課堂鎖定120分，像第23題第（2）題、第24題第（2）題、第25題第（2）（3）題無人會解或極個別學生解出部分的題目，課后個性化培優處理是注重不同層次學生的不同需求，盡量不浪費絕大部分學生的時間，提高教學實效。

二、 共性錯誤，歸類剖析，提高課堂的實效

對知識的學習和掌握打一個比方：如果把知識比作一顆顆晶瑩剔透的珍珠，學生比作拾珍珠的人，若粒粒散散的捧在手里，一裝不了多;二肯定容易隨時丟落。若用細繩把它們串聯就能如愿獲得所有珍珠。的確，知識也只有善于歸類，才能使知識結構化、條理化、系統化，才有利于深層理解和有效掌握。類似地，老師在講評課時，逐題孤立講解，不僅費時、煩瑣，而且失去讓學生觀察、類比、聯想、轉化等能力的培養機會，應該引導學生對試卷上多數的共性錯誤進行歸類：是對概念、公式、法則、定理記憶不牢，理解不透，或理解錯誤？還是審題不嚴，對字、詞、句解讀有偏差？是計算沒有根據算理算法出錯，還是方法策略失當？針對錯因，把相關聯的題目歸類，對癥下藥，在知識的整合和對比中，使學生對這類問題形成一個整體感，有助于學生有序、清晰地理解知識間內在關聯，構建自身的新認知，也有利于知識持續生長和創新，為后續的學習提供不竭的動力，這才是真正的高效。

上面提到的送教下鄉的試卷講評課，根據試卷分析結果，絕大部分同學解答好的題目課堂不講，共性、典型問題歸五類剖析。先按知識內容歸類：像第8、14、23（1）題涉及統計概率知識歸為一類，重點回顧相關概念，并配以相應練習，鼓勵學生這類題志在必得;像7、22題是中考必考的應用題歸為一類，側重復習應用題解題策略，如何找等量關系列方程，讓學生對解應用題有自己熟練的方法;第18、20、21題是幾何證明題歸為一類，學生書寫不規范、不嚴謹，推理能力薄弱，課堂上注重講析幾何證明的技巧——讀題、標圖、聯想，同時拍照上傳書寫不規范的試卷，讓學生辨析，避免重蹈覆轍;圓是很多學生頭疼的內容，有些學生干脆遇圓繞道，自己心里先定位不會，但中考涉及圓的內容往往不是很難，像第8、24（1）題就是考查圓的相關知識歸為一類，發現圓也沒有那么難，目的在于激勵學生不放棄;最后按試卷中的思想方法把第10、13、15、16題歸一類講析，它們分別應用了分類、整體、轉化、數形結合等思想方法，讓學生明白數學思想方法是數學的靈魂，時刻在用。分門別類之后課堂上創設民主、合作、探究的情景，通過師生互動、生生互動，引導學生答疑釋疑、整合知識、總結方法規律、啟迪思維，在緊湊、有序、愉悅中完成了教學任務。

三、 善用試卷中的好題，發揮學生的主體性，培養學生的思維能力

一遇難題，老師常感嘆，類似的題目學生做過了、講評過了，有時還多次做過、講評過，考試依然很多學生不會，說明學生存在著思考缺欠甚至誤區。老師講評過的內容，囫圇吞棗，沒有內化為自己的認知方式，學生的思維還停留在原有水平上。若試卷講評課只是就題論題，相當于穿新鞋走老路，沒有提升學生的思維水平，解題時難以跨越題目的思維障礙。史寧中教授在《數學教育的未來發展》中闡述過，數學教學應當承擔起提升一個人未來思維能力的重擔。因此，數學試卷講評課只有承擔起培養學生的思維能力的重擔，方顯出課堂的實效。

一份試卷常有個別題目很出彩，原型來自課本，不偏不怪不叼，有針對性和綜合性，既考查多個知識點的聯系，又滲透多種方法、策略和思想，難度適中，對學生又具有挑戰性。老師要善于發現這種好題，發揮老師的主導作用，突出學生的主體地位，點撥學生一題多解，培養學生思維多樣性和創新能力，在對比中總結思想方法;或變式拓展，牽引學生思維的發展和完善;也可以師生互換角色，共同探討挖掘學生思維潛力等。在老師主導下，讓學生去探索，大膽猜想、凝練觀點、提出問題，喚醒創新意識，使學生真正成為講評課的主人。在多角度、全方位的探索感知實踐中，優化知識結構，培養思維能力，為后續學習助力，提升學生學習數學的核心競爭力。

筆者在評講2019～2020學年第一學期九年級期中檢測卷時，發現第16題就是典型好題。以下是筆者的處理方式，供大家批評指正。原題展現：已知菱形ABCD在平面直角坐標系中的位置如圖1所示，頂點B（10，0），AC=85，點E的坐標是（0，2），點M是對角線AC上的一個動點，當MD+ME最短時，點M的坐標是。

分析點評：這是一道幾何、代數綜合題，涉及菱形、直角坐標系、一次函數、三角形相似等眾多知識，綜合考查學生整合知識熟練程度及分析問題、解決問題的能力。教學過程再現：師生共同互動分析幾何解題套路——讀題、標圖、聯想，所謂聯想就是已知可知，未知還需要什么。引導學生回顧線段和最值策略“化同為異、化折為直”，學生發現這是兩定一動模型，來自課本中的練習——兩村在公路上建奶站問題。因此，只需作D或E關于AC的對稱點，然后連接E或D與對稱點交AC于一點M，即可確定M的位置。因為菱形是軸對稱圖形，點B、點D關于AC對稱，所以連接BE交AC于點M，點M就是所求作的。如何求點M的坐標呢？老師點撥、引導學生一題多解，目的在于培養學生思維的多樣性。請生1講演思路，生1用函數知識解決問題：如圖2，連接BD交AC于點F，因為四邊形 ABCD 是菱形，所以AC⊥BD，AF=12AC=45，在 Rt△ABF 中，根據勾股定理求出BF=25，過點F作FN⊥AB，垂足為N，根據面積不變，12AF·BF=12AB·FN求出FN=4，在Rt△FAN中，根據勾股定理得AN=8，所以F（8，4），求出直線AC的解析式為y=12x，由B（10，0）、E（0，2）求出BE的解析式為y=-15x+2，聯立y=12xy=-15x+2，解得x=207y=107，求得M207，107。請生2講演思路，生2用三角形相似知識求解：如圖3，過點M作MG⊥AB，垂足為G，因為四邊形ABCD是菱形，所以AC⊥BD，所以∠AFB=90°，因為MG⊥AB，所以∠AGM=90°，得∠AFB=∠AGM，又由∠BAF=∠MAG，得△ABF∽△AMG，得BFAF=MGAG=2545=12，設MG=t，則AG=2t，易證△MGB∽△EAB，得MGAE=BGAB得t2=10-2t10，解得t=107，所以MG=107，AG=2t=207，得 M207，107。通過一題多解，變通求法，整合了知識結構，使一次函數、點的坐標、菱形、三角形相似等知識有機融合在一起，生成為學生的新認知。教師還可以跟學生互換角色，拓展外延，激發學生思考，如追問：剛才是在菱形的背景下考了兩定一動模型，還可以考什么呢？請學生出題。學生根據學習經驗回答，可以考一定兩動模型。請生3出題：如圖4，在AC、AB上找點M、G，使MG+MB最短，求點M的坐標。師解答分析：解題策略相類似，還是“化同為異，化折為直”，連接MD，根據菱形的對稱性，得MD=MB，所以要求MG+MB最短，只需求MG+MD最短，由“垂線段最短”原理，過點D作DG⊥AB，垂足為G，則DG交AC于點M，這時點M就是所求作的點。

四、 課后跟進落實，端正學習態度，培養學習習慣

雙減政策下，課堂45分鐘是老師的主陣地。為了課堂提質增效，不浪費絕大多數學生的時間，試卷講評課無法當堂解決所有學生的所有問題，個別學生的不具有代表性的問題要求學生課外自行訂正，積極主動地尋找解決辦法，并做好錯因分析說明，課后老師要一一落實問題解決情況，讓學生的錯誤不留死角，培養學生有錯必究的良好習慣，形成積極主動解決問題的態度。課后根據講評課反饋的情況，布置3、4道作業進行刻意學習，鞏固最重要的知識技能，為后續學習打下堅實的知識基礎。

在試卷講評課中，忌諱面面俱到、平均使力，應該以恰當的方式，抓住學生問題的“要害點”，抓準學生思維提升的“盲點”，在學生最近發展區做精辟的演繹，引領學生從紛繁復雜的內容中理清頭緒，抓住問題的本質，突破難點，這才是真正的追求高效。把握好“講”與“不講”、“講多”與“講少”、“精講”與“多練”教學節奏，優化課堂，為學生的思考提供足夠的時間和空間，把學習的主動權還給學生，使學生在主動、積極的情感狀態下掌握知識和技能，培養分析問題和解決問題的能力。

參考文獻：

[1]韓新正.談數學課堂教學的節奏之美[J].中小學數學，2013（9）.

作者簡介：林巧容（1975～），女，漢族，福建寧德人，福建省寧德市蕉城區蕉城中學，中學一級教師，研究方向：初中數學。