一種面向智能汽車的工況自適應路徑跟蹤控制方法

江浩斌，韋奇志，李傲雪，唐 斌，耿國慶

(1.江蘇大學 汽車與交通工程學院， 江蘇 鎮江 212013； 2.江蘇大學 汽車工程研究院， 江蘇 鎮江 212013)

0 引言

智能汽車是一種集環境感知、規劃決策、跟蹤控制等功能于一體的復雜系統，被視作解決道路安全事故、交通擁堵等問題的理想方案，近年來一直是各國政府、高校以及相關企業的重點研究對象[1]。作為智能汽車的三大核心技術之一，路徑跟蹤系統的主要功能是根據環境感知以及規劃決策模塊提供的信息，通過控制車輛轉向與速度，沿規劃好的參考路徑行駛，并保持路徑跟蹤的精確性和穩定性[2]。目前，針對智能汽車路徑跟蹤的理論主要有預瞄-跟隨理論，比例積分微分(PID)理論、線性最優二次型(LQR)理論、滑膜控制理論、模糊自適應控制理論和模型預測控制(MPC)理論等[3-7]。其中，MPC是基于模型反饋和優化的控制理論，主要由預測模型、滾動優化和反饋校正等部分組成。MPC控制器加入了被控對象的動力學約束條件，是求解復雜系統多目標優化問題的理想方法[8]，近年來被廣泛應用于智能汽車路徑跟蹤控制的研究。

雖然現有的MPC路徑跟蹤控制器已經能夠在很多工況下完成自動駕駛任務，但其在惡劣路面下的路徑跟蹤控制效果依然不理想。何杰等[9]通過ADAMS/Car實驗表明，路面附著系數對行車安全性具有明顯影響，車輛在雨雪天和結冰路面條件下，容易失去控制，偏離車道，發生碰撞危險。楊博等[10]提出考慮防碰撞與防側翻的避障路徑規劃與跟蹤控制，基于MPC理論設計出避障路徑跟蹤控制器，仿真結果表明，極限工況下車輛LTR值明顯增大，跟蹤控制效果不佳。辛喆等[11]搭建了基于Carsim/Simulink的聯合仿真試驗平臺，利用YALMIP和GUROBI構建求解MPC問題，在低附著路面工況下，MPC 控制器犧牲了部分路徑跟蹤的性能以保持車輛的橫向穩定性。現有針對智能汽車路徑跟蹤控制的研究主要是在單一工況的條件下進行的，對于低附著路面、復雜突變道路工況的控制方法研究較少。

為優化MPC控制器在復雜路面條件下的路徑跟蹤控制效果，筆者提出了一種面向智能汽車的工況自適應路徑跟蹤控制方法，首先建立三自由度車輛動力學模型，基于模型預測控制原理，設計了智能汽車路徑跟蹤控制器；然后求取了不同路面附著系數下的路徑跟蹤最優車速。根據《中國公路路線設計規范》劃分了88種典型工況，在傳統模型預測控制理論的基礎上，利用遺傳算法優化得到不同工況下最優時域參數。將縱向車速和道路曲率反饋引入MPC控制器實時匹配最優控制參數，從而實現工況自適應的路徑跟蹤控制，最后通過Carsim/Simulink平臺聯合仿真對該方法進行驗證。

1 車輛動力學模型的建立

本文主要研究不同道路工況對前輪轉向車輛路徑跟蹤的影響，三自由度車輛動力學模型能夠較為準確地反映車輛路徑跟蹤過程中的橫向、縱向、橫擺動力學特性，因此，建立簡化的三自由度車輛動力學模型作為MPC的預測模型。首先做出如下假設：①車輛行駛于水平路面，忽略側傾和垂向運動；②將車輛前、后軸簡化為單軌，忽略載荷左右轉移；③ 輪胎縱向滑移率和側偏角較小，輪胎力處于線性區。

據此建立的三自由度車輛動力學模型如圖1所示。

圖1 車輛三自由度動力學模型

圖1中，OXY為大地慣性坐標系；oxy為車輛坐標系；a、b為車輛前、后軸到質心的距離；Fx,f、Fx,r為前、后輪沿x軸方向的受力；Fy,f、Fy,r為前、后輪沿y軸方向的受力。

根據牛頓第二定律，將該模型轉化為受力平衡方程形式，可得：

(1)

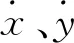
根據前文假設，車輛前、后輪所受縱向力可簡化表示為：

F1,f=Cl,fSf，F1,r=Cl,rSr

(2)

式中：Cl,f、Cl,r為前、后輪縱向剛度，Sf、Sr為前、后輪滑移率。

前、后輪所受側向力可簡化表示為：

(3)

式中：Cc,f、Cc,r為前、后輪側偏剛度。

將大地慣性坐標系與車輛坐標系之間的關系進行轉換，可得：

(4)

聯立式(1)—(4)，可得簡化后的三自由度車輛動力學模型表達式：

(5)

2 基于MPC的路徑跟蹤控制器設計

2.1 線性時變模型

車輛在高速行駛時對控制器的實時性要求高，前文所推導的非線性模型難以滿足要求，因此將式(5)線性化，得到線性時變狀態方程：

(6)

將式(6)采用一階差商法進行離散化處理，可得：

(7)

引入增量模型后的狀態空間表達式為：

(8)

式中：Ak,t=I+TAdyn(t)，Bk,t=TBdyn(t)，I為單位矩陣，T為采樣周期。

2.2 預測方程

預測方程是MPC控制器的重要組成部分，能根據已有信息和當前輸入來預測系統未來的輸出。將式(7)轉換為：

x(k|t)=[ξ(k|t)u(k-1|t)]T

(9)

得到新的狀態空間表達式：

(10)

定義k時刻系統輸出和輸入分別為：

Y(k+1|k)=[y(k+1|k),

y(k+2|k),…,y(k+Np|k)]T

ΔU(k)=[Δu(k|k),Δu(k+1|k),…,

Δu(k+Nc|k)]T

(11)

式中：Np、Nc為系統的時域參數，Np>Nc。

可得系統未來預測方程的表達式：

Y(k+1|k)=ψkξ(k)+ΘΔU(k)

(12)

2.3 約束條件

為了保證基于動力學模型的MPC控制器路徑跟蹤的穩定性和精確性，需要在控制器的設計中添加車輛動力學約束條件。

1) 質心側偏角約束

高附著路面約束條件為-10°≤β≤10°；低附著路面約束條件為-2°≤β≤2°。

2) 輪胎側偏角約束

當輪胎側偏角≤5°時，為使車輛在低附著路面有良好的行駛穩定性，將輪胎側偏角限定為-2.5°≤af≤2.5°。

3) 路面附著條件約束

車輛行駛時，側向加速度與路面附著系數的關系可近似為ay≤μg。為防止系統求解時出現無可行解的情況，將路面附著系數設定為軟約束條件ay,min-ε≤ay≤ay,max+ε。

2.4 優化求解及反饋矯正

由于使用了車輛動力學模型，同時也加入了較多約束條件，為減小計算復雜度，提高系統運行效率，故在MPC控制器的目標函數中加入松弛因子，其表達式為：

(13)

式中：Δy(t+i|t)為參考路徑和系統輸出的差值；Δu(t+i|t)為系統控制增量；Q和R分別為系統輸出量和控制增量的權重矩陣；ρ為權重系數，ε為松弛因子。

根據以上目標函數和約束條件，路徑跟蹤控制器在每個周期內要進行以下優化問題的求解：

(14)

系統在每個控制時域內求解得到控制增量序列：

(15)

將其中的第一個元素作為實際控制增量輸入系統，可得：

系統進入下一個控制時域后，不斷重復以上過程，以此實現對參考路徑的跟蹤。至此建立了基于MPC理論的智能汽車路徑跟蹤控制器。

2.5 車速對MPC跟蹤效果的影響

基于MPC原理搭建了Carsim/Simulink聯合仿真平臺，分析單一路面附著系數下，不同車速對MPC控制器雙移線路徑跟蹤效果的影響。部分車輛參數如表1所示，路面附著系數為0.8。MPC控制器中的預測時域Np和控制時域Nc為固定值，分別設為20、3。

表1 仿真車輛參數

在μ=0.8的雙移線仿真工況下，幾組不同車速的路徑跟蹤仿真結果如圖2所示。在高附著工況下，MPC控制器對于車速變化具有一定的魯棒性，速度增加并不會導致車輛穩定性能的明顯下降，但單一參數的MPC控制器路徑跟蹤誤差會逐漸增大。這是因為在固定控制參數下，當車速增加時，在相同控制時域內車輛的行駛距離增加，使車輛在各個控制周期內的預測距離增大，從而導致車輛的動態響應性能降低；當道路曲率半徑減小時，由于預測時域不變，車輛的路徑跟蹤精度也會隨之降低。

圖2 不同車速下路徑跟蹤仿真效果

3 路面附著系數與最優跟蹤車速的關系

3.1 路徑跟蹤綜合評價指標

本文研究的重點是不同路面附著系數下智能汽車自適應路徑跟蹤控制，因此需要確定車輛在不同路面附著系數下的最優車速。車輛本身是一個復雜的多自由度非線性時變系統，為了更加客觀合理地評價車輛路徑跟蹤中的動態特性，需建立綜合評價指標分析不同仿真工況下的智能汽車路徑跟蹤效果。

郭孔輝教授提出了利用“總方差法”對汽車操縱性能進行有效的評價[12]，本文在該方法的基礎上建立了基于操縱穩定性、跟蹤精確性、行駛最速性3個方面的路徑跟蹤綜合評價指標。

1) 操縱穩定性評價指標

包括橫擺角速度指標:

(16)

側向加速度指標：

(17)

側滑危險性指標：

Jl=max(Jl1,Jl2)

(18)

其中，包括前軸側滑危險性指標：

(19)

后軸側滑危險性指標：

(20)

取上3項加權平均，得到操縱穩定性評價指標：

(21)

式中：wr1、wr2、wl分別為Jr1、Jr2、Jl對應加權值。

2) 跟蹤精確性評價指標

包括側向偏差指標：

(22)

方向偏差指標：

(23)

取上2項加權平均，得到跟蹤精確性評價指標：

(24)

式中：we1、we2分別為Je1、Je2對應加權值。

3) 行駛最速性評價指標

(25)

4) 路徑跟蹤綜合評價指標

將以上3項指標作加權平方根處理，得到路徑跟蹤綜合評價指標：

(26)

式中：w1、w2、w3分別為JS、JE、JU對應加權值，JC值越小，路徑跟蹤效果越好。

各項指標的動力學參數閾值和權值的選取參考文獻[13]，動力學參數閾值如表2所示。

表2 各項動力學參數閾值

3.2 求解不同路面附著系數下的最優跟蹤車速

將路面附著系數從1.0～0.1分成10組進行雙移線仿真實驗，統計不同車速下，每一組工況仿真過程中的側向偏差、質心側偏角、橫擺角速度等動力學參數，并計算路徑跟蹤綜合評價指標。

依據路徑跟蹤綜合評價指標JC，計算得到不同μ下評分最優的試驗車速集合Vi，如表3所示。可以發現，隨著路面附著系數的降低，綜合評價最優車速不斷減小，這也符合人類在現實道路條件下的駕駛習慣。

表3 綜合評價最優車速 km/h

通過5次多項式擬合，得到不同的μ與綜合評價最優車速的關系，如圖3所示。

圖3 路面附著系數與最優車速的擬合關系曲線

4 時域參數自適應路徑跟蹤控制器

4.1 劃分典型彎道工況

傳統MPC控制器中的時域參數通常離線確定，且在優化過程中保持恒定，影響了其針對不同工況的魯棒性，為了提高MPC算法在不同車速以及不同曲率工況下的跟蹤精度，需要在MPC控制器中引入縱向車速和道路曲率半徑反饋，分析匹配最優控制參數，實現控制參數自適應，從而更加準確地反映智能汽車行駛過程中的動態特性，實現復雜工況下的路徑跟蹤。

根據《國家公路路線設計規范 JTG D20—2017》，各級公路在設計彎道最小半徑時，應與其設計速度相適應。表4為不同設計車速所對應的最小道路曲率半徑。

表4 彎道工況設計規范

依據表4可知，車輛行駛在實際道路上時，其轉彎半徑應大于等于該路段設計車速下對應的最小道路曲率半徑。依據表3定義智能汽車路徑跟蹤車速取值范圍為10～80 km/h。利用均勻性設計思想，以設計車速所規定的最小道路曲率半徑為基準，劃分如表5所示的88組不同的典型彎道工況。

表5 典型彎道工況

4.2 基于遺傳算法求解各工況下的最優時域參數

根據已有的研究可知，MPC控制器中的最優時域控制參數Np和Nc會受到縱向車速變化的影響[14]。如果取值過小，且速度較快時，車輛無法及時跟蹤期望轉角，最終導致路徑跟蹤控制失敗；如果取值過大，則會增加系統的計算量，導致當前位置附近的跟蹤誤差增大，不利于路徑跟蹤控制器的實時性。因此，需要確定MPC控制器在不同彎道工況下的最優時域參數組合。但考慮到劃分的典型彎道工況較多(88組)，用枚舉法很難求出最優解。

遺傳算法擁有強大的全局搜索能力、收斂速度快和搜索效率高等優點[15]，故選擇利用Matlab中的Genetic Algorithm Toolbox工具箱調用遺傳算法對時域參數進行優化。

確定優化目標為MPC控制器的時域參數矩陣K1=(NpNc)。為提升優化效率，預測時域取值范圍Np∈(0，40]，控制時域取值范圍Nc∈(0，20]。適應度函數為第3節所求得的不同仿真工況所對應的路徑跟蹤綜合評價指標：

具體優化步驟如下：

1) 初始化時域參數矩陣，生成N個個體的種群；

2) 運行路徑跟蹤模型，計算相應個體的適應度函數；

3) 選取評分高的個體進行迭代優化，生成新的個體；

4) 為避免局部最優，隨機選擇少量進行變異操作。

設置遺傳算法的初始種群數量為50，優化代數為20，交叉概率為0.5，變異概率為 0.1，算法優化流程如圖4所示。

圖4 遺傳算法優化流程框圖

將各組迭代優化后所對應的預測時域與控制時域作為對應工況下的最優時域參數組合，優化后結果如表6所示。

可以發現，在不同車速與道路曲率半徑工況下，為使智能汽車具有最佳的路徑跟蹤精度及行駛穩定性，MPC控制器應選取不同的預測時域、控制時域。

4.3 建立時域參數自適應的MPC控制器

基于Simulink/Carsim聯合仿真平臺，在原有模型的基礎上建立了時域參數自適應的MPC控制器。車輛在路徑跟蹤時，根據當前路面附著系數進行最優車速跟蹤，系統實時輸入當前車速和道路曲率半徑，并根據表6將所求得的最優預測時域與控制時域組合(NpNc)輸入模型預測控制器，以此得到時域參數自適應的智能汽車路徑跟蹤控制器，其系統整體結構如圖5所示。

圖5 自適應路徑跟蹤控制器系統整體結構

5 仿真試驗

為了驗證本文提出的考慮路面附著系數的自適應路徑跟蹤模型在對接路面工況的有效性，仿真試驗設置了3種控制器對比控制效果，分別是：時域參數自適應MPC、僅加入最優車速約束的MPC和傳統MPC。在Carsim中設定路面附著系數條件，仿真時通過設置Carsim中Target speed vs.station模塊完成對期望速度的跟蹤。圖6為路面附著系數變化情況，路面附著系數在60 m處由0.8變為0.3。

圖6 路面附著條件變化

圖7為路面附著系數由高到低的對接路面雙移線仿真結果。圖7(a)為車輛的期望最優車速與實際跟隨車速變化，傳統MPC的跟蹤車速為定值60 km/h；圖7(b)-圖7(d)為車輛在不同控制器下的跟蹤路徑、側向偏差、橫擺角速度變化。由圖7可知，在仿真開始時，3種控制器在高附著路面均有較好的控制效果。在車輛行駛至60 m后，路面附著條件發生變化，傳統MPC控制器仍然以定速在低附著路面進行路徑跟蹤，側向偏差與橫擺角速度明顯增大；加入最優車速約束的MPC控制器能應對路面附著系數突變的工況，但由于采用固定的時域控制參數，導致在低附著路面下跟蹤誤差較大；自適應MPC控制器根據工況變化采用合適的車速和時域控制參數進行路徑跟蹤，跟蹤精度與穩定性最佳。

圖7 對接路面仿真結果

為了驗證該模型針對不同曲率工況的有效性，在Carsim中設置變曲率彎道工況并進行仿真試驗。參考路徑由一段蛇形、一段左轉、一段移線工況拼接而成，路面附著系數為0.8，仿真車速均為60 km/h，對比時域參數自適應MPC控制器和傳統MPC控制器跟蹤效果。仿真結果如圖8(a)-圖8(d)所示。由圖8可知，在單一路面附著系數的變曲率工況下，2種控制器均能完成路徑跟蹤，相比于傳統MPC控制器，本文提出的時域參數自適應MPC在確保行駛穩定性的前提下，能有效提高跟蹤精度。

圖8 變曲率彎道仿真結果

不同控制器的路徑跟蹤仿真結果統計對比如表7所示。統計結果顯示，本文所提出的自適應路徑跟蹤模型在對接路面雙移線仿真試驗中的最大側向偏差為0.33 m，橫擺角速度峰值為8.81(°)/s；在變曲率彎道仿真試驗中的最大側向偏差為 0.36 m，橫擺角速度峰值為8.47(°)/s。相比于傳統MPC路徑跟蹤模型，能夠有效提高車輛在不同路面附著系數和道路曲率下路徑跟蹤的精確性和穩定性。

表7 不同控制器仿真結果

6 結論

1) 建立了三自由度車輛動力學模型，基于模型預測控制原理設計了智能汽車路徑跟蹤控制器，通過Simulink/Carsim聯合仿真顯示，固定時域參數的MPC控制器跟蹤誤差隨著車速的提高而增大。

2) 為提高傳統MPC控制器在不同路面附著系數及不同曲率工況下的路徑跟蹤性能，基于總方差法建立了路徑跟蹤綜合評價指標，確定了不同路面附著系數下的最優跟蹤車速，利用遺傳算法優化求解各彎道工況下MPC控制器的最優時域參數，設計了時域參數自適應路徑跟蹤控制器。

3) 進行了對接路面雙移線和變曲率彎道仿真，結果表明，相比于傳統MPC路徑跟蹤控制器，本文所提出的時域參數自適應路徑跟蹤控制器可以根據不同的路面附著條件和彎道曲率采用合適的時域控制參數進行路徑跟蹤，對道路工況變化具有良好的魯棒性，有效提高了復雜路面條件下的路徑跟蹤精確性和行駛穩定性。