無人車典型場景構建及車速預測
宋傳杰,高建平,謝詔璽,郗建國
(河南科技大學 車輛與交通工程學院, 河南 洛陽 471003)
0 引言
隨著汽車智能化、網聯化的深度發展,智能駕駛汽車的安全問題成為關注的焦點。構建合理的自動駕駛汽車測試與評價系統,需對真實環境中的危險場景進行分析與構建。當前,自動駕駛汽車的測試評價對象已從傳統的人-車系統轉變為人-車-環境交互耦合系統,而測試場景已成為不可或缺的環節[1-2]。目前,國內外對測試場景及場景要素的形式還存在爭議,標準中也未進行明確闡述。場景生成方法可分為基于演繹的方法和基于歸納的方法。郭景華等[3]、徐向陽等[4]基于歸納的方法,通過采集的真實交通數據構建測試場景,且處于仿真階段。Xia等[5]利用層次分析法衡量場景要素的重要度,通過獨立組合測試方法將離散的測試用例聚類成連續場景,確保了場景覆蓋的全面性,但生成的場景不具有典型性。基于當前自動駕駛汽車測試現狀,測試場景應具有代表性強、數量少等特點。
目前,科學理論技術提升了自動駕駛汽車的預測能力。熊曉夏等[6]基于支持向量機和混合高斯的隱馬爾可夫鏈模型對道路事故進行預測,但對我國交通環境下網聯車輛的前車狀態考慮較少。張金輝等[7]采用貝葉斯網絡對前車車速進行預測,將得到的跟車數據分為訓練集和測試集,通過測試集檢測前車車速預測效果,但預測精度有待提高。倪捷[8]在構建預測模型時,僅考慮了車輛的運行特征,而忽略了交通環境對行車風險的影響,不能全面反映行車狀態。綜上所述,由于我國交通環境復雜度較高,車輛未來狀態受駕駛員等多種因素影響,自動駕駛車輛對前車運行狀態難以進行精確預判。
基于以上問題,本文以自動駕駛車輛為研究對象,對典型場景下自動駕駛車輛前車車速進行預測,選取對事故類型影響較大的特征要素。采用Prescan、Matlab/Simulink等工具和優化算法,構建基于馬爾科夫鏈和循環神經網絡的前車車速預測模型,通過模擬狀態與原始狀態的對比,驗證了預測模型的有效性。最后,將車速模型參數導入整車控制器中,并進行試驗驗證。
1 測試場景要素分析
1.1 數據來源
本文數據來源于國家車輛事故深度調查系統(national automobile accident indepth investigation system,NAIS),由多所高校和研究機構共同建立。該數據圍繞事故相關的人-車-路-環境信息進行深入采集,涵蓋全國具有代表性的區域,且與我國道路事故統計特征基本吻合[9]。結合NAIS數據庫和自動駕駛測試場景要求,考慮到測試過程中,測試車輛本身與周圍場景的相互作用,因此,將場景要素分為交通環境要素和測試車輛基礎信息要素兩大類,如圖1所示。
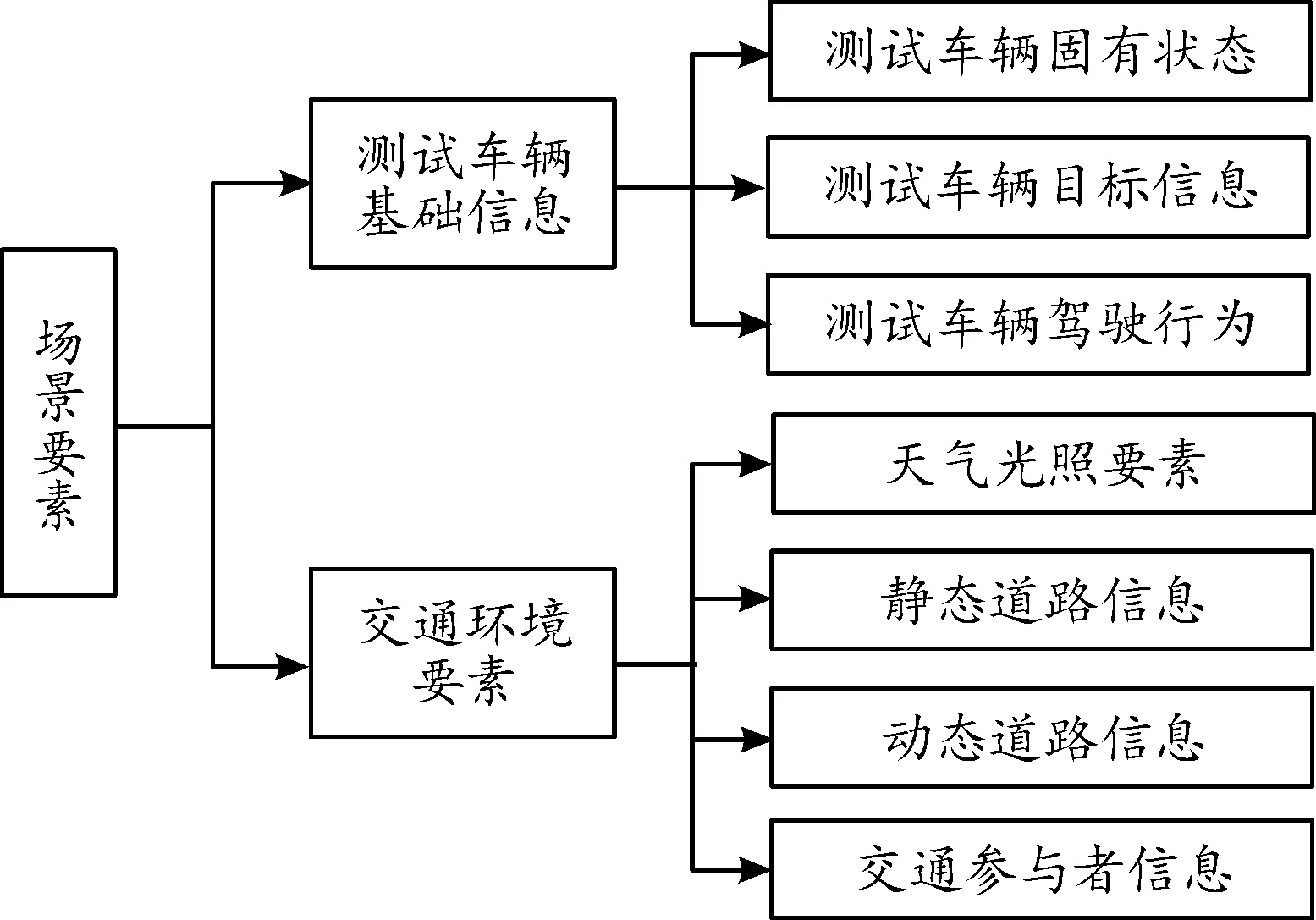
圖1 場景要素分類
1.2 場景要素編碼
為了構建場景要素指標體系,需要對各場景要素進行編碼。根據實際駕駛經驗,本文以交通環境要素中的事故時間、天氣、道路狀況、道路流量、路面材質、道路類型為自變量,事故類型為因變量,使用SPSS軟件進行多元線性回歸分析,探究各要素對事故類型的影響程度。多元線性回歸模型能較好地兼顧各個要素的權值。此外,為避免個別要素取值過于離散,在編碼過程中將相近的屬性進行合并。要素編碼情況如表1所示。
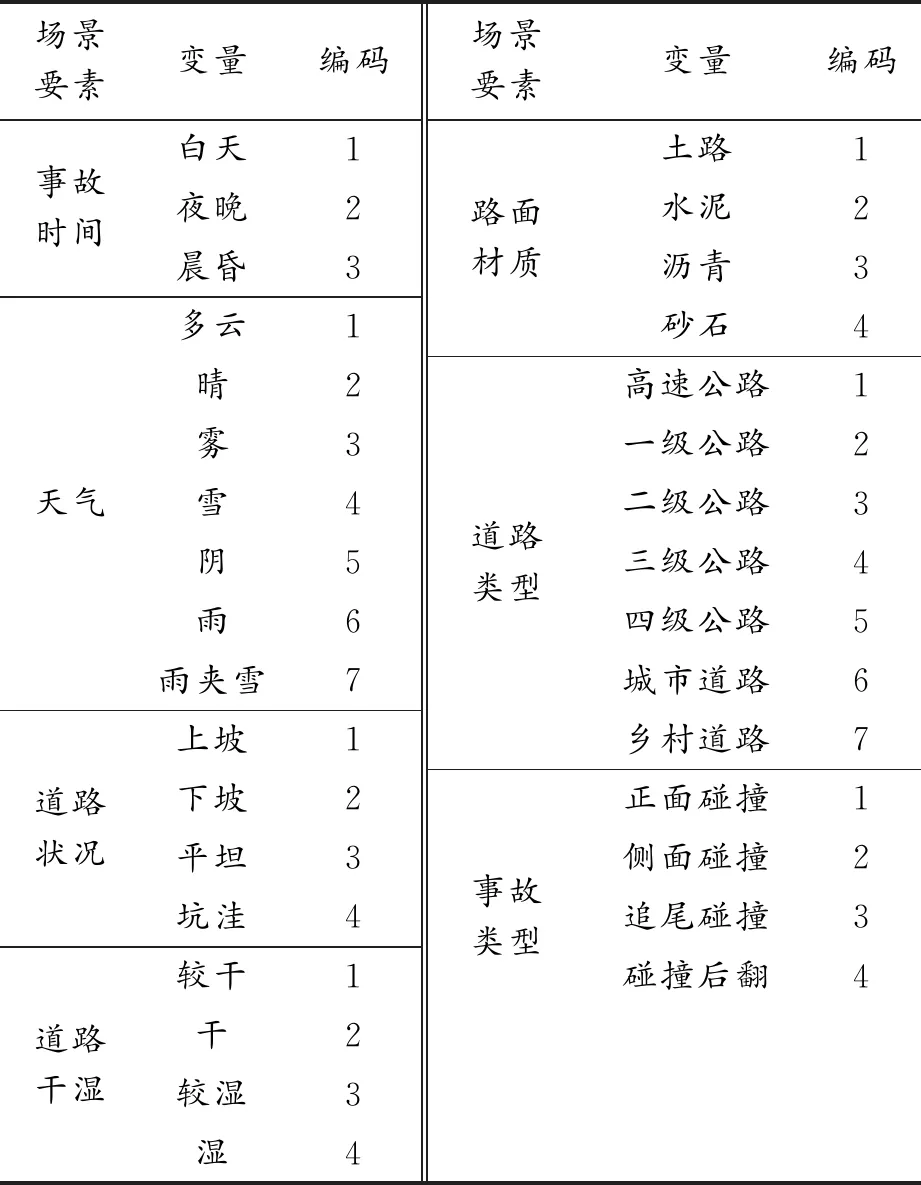
表1 要素編碼
1.3 多元線性回歸模型構建
事故類型的線性回歸模型為:
(1)
式中:Y為事故類型;x為對事故類型有顯著影響的自變量;p為自變量個數;n為樣本總數;βp為第p個變量的回歸系數,εi為第i個樣本的隨機誤差[10]。由式(1)可得n個樣本的矩陣隨機表達式:
Y=xβ+ε
(2)
假設x的列滿秩,則回歸系數的最小二乘估計量為:
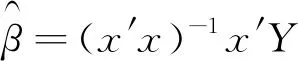
(3)
多元線性回歸過程中還需對樣本回歸函數進行檢驗,以判斷預測的可靠程度,包括擬合優度、顯著性水平、德賓-沃森值等。
擬合優度檢驗即通過樣本回歸對觀測值進行擬合,記

(4)
為總離差平方和,
(5)
為回歸平方和,
(6)
為殘差平方和,則:
(7)
式中,R2為可決系數,其大小可表示自變量對因變量的貢獻程度,其值越接近1,表明擬合優度越高。
在原假設成立的前提下,顯著性檢驗的統計量由
(8)
公式確定,查表可得臨界值Fα,通過比較F和Fα的大小來判斷原假設H是否成立,一般情況下顯著性水平取0.05或0.1。
1.4 多元線性回歸結果
本文多元線性回歸分析中,置信區間設為95%,模型信息如表2所示,回歸分析結果如表3所示。根據R2,表明各要素預測事故類型的準確性較強。
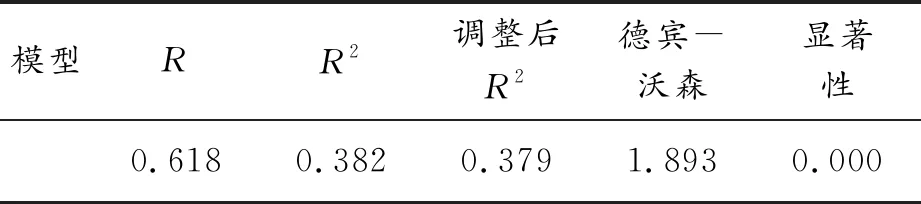
表2 模型信息
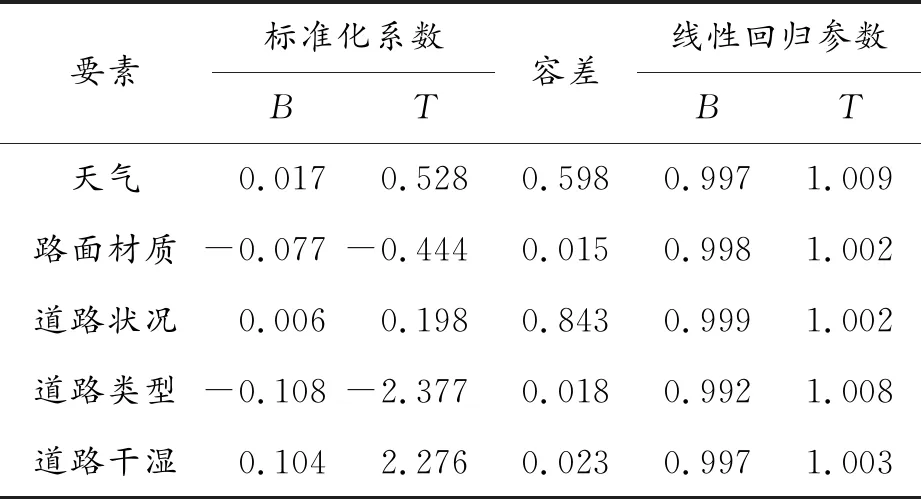
表3 回歸分析結果
結合表2和表3數據,根據德賓-沃森值和VIF值,可說明樣本數據隨機性較強且多重共線性呈弱相關,顯著性水平<0.001,表明模型預測效果較好。取顯著性水平為0.05,根據分析結果,路面材質、道路類型和道路干濕對事故類型影響較大,而天氣、道路狀況對事故類型影響較小。
基于以上分析,將路面材質、道路類型和道路干濕確定為特征要素,特征要素即對事故類型影響較大的要素。由于自動駕駛車輛感知系統容易受能見度的影響,因此,將能見度作為測試場景的特征要素[11]。
2 測試場景K-均值聚類挖掘
2.1 K-均值聚類算法
為挖掘出具有代表性的測試用例,采用聚類算法對測試場景進行聚類挖掘,剔除重復或相似的測試用例,得到代表性較強的測試用例。K-均值聚類分析算法作為一種快速聚類算法,其對計算機的性能要求不高,且可應用于比系統聚類法大得多的數據組[12]。
K-均值算法流程為:首先,將所有樣品分為K個初始類;然后,計算某樣品到各類中心的歐幾里得平方距離,將樣品分配給最近的一類。對于有變動的類,重新計算其坐標,為下一步聚類做準備。無變動的類輸出后成為一類[13]。聚類算法的流程如圖2所示。
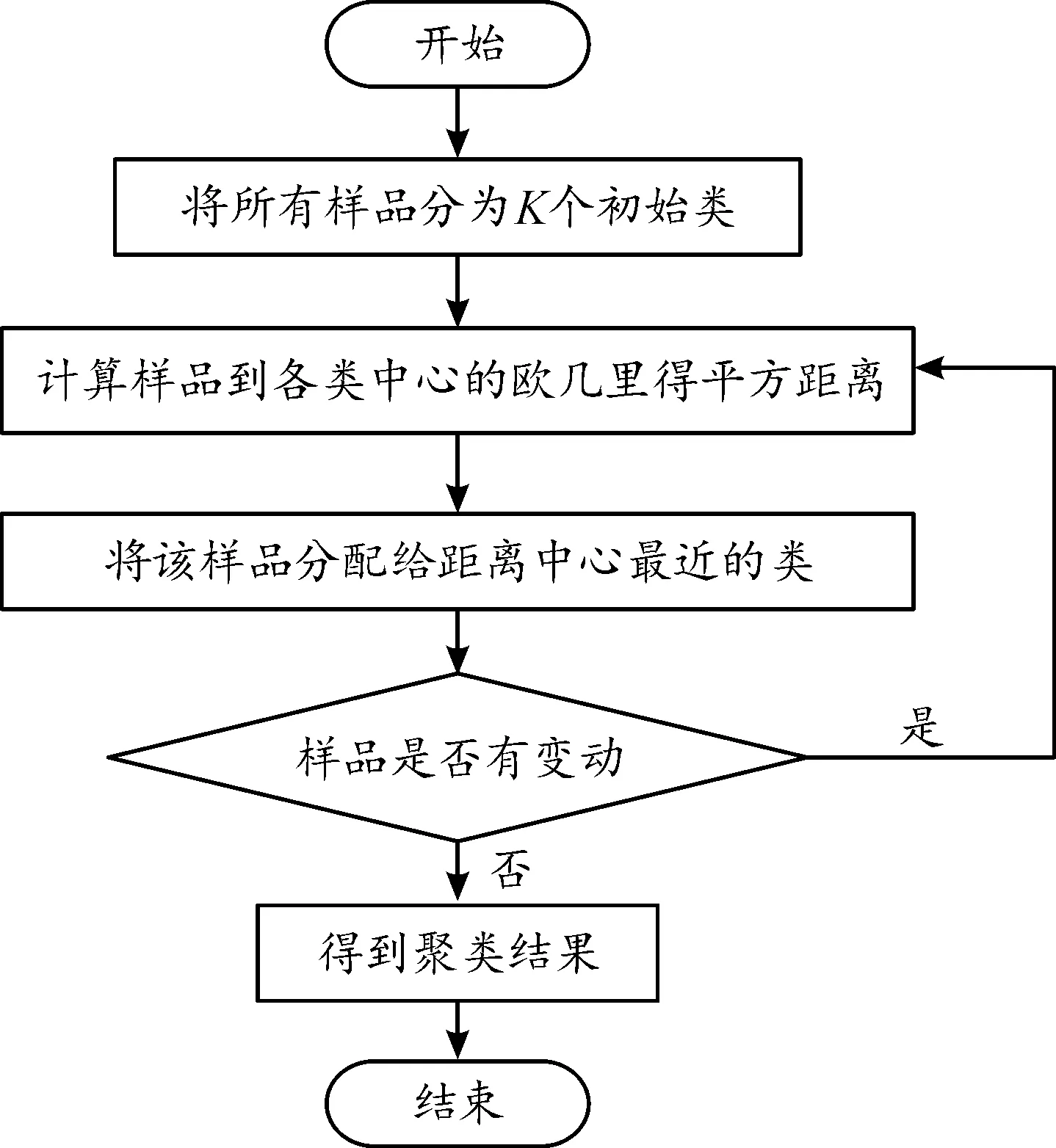
圖2 K-均值聚類算法流程
其中歐式平方距離公式為:
(9)
式中:I=(xi1,xi2,…,xif)和J=(xj1,xj2,…,xjf)是2個f維的數據對象,f為變量個數,xik為第i個樣本中第k個變量的度量值。此外,采用最長距離法定義類與類之間的距離,規定相同變量間距離為0,不同變量間距離為1。首先,將各樣品自成一類;然后將距離最小的兩類合并。其中,定義類Gi與類Gj之間的距離為最遠樣品的距離,公式為:
(10)
式中:dij為樣品Xi與Xj之間的距離;Dpq表示類Gp與Gq之間的距離。將類Gp與Gq合并為Gr,則任一類Gm與Gr的類間距離為:
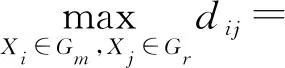
max{Dmp,Dmq}
(11)
2.2 測試場景聚類結果
選取第1節的4個特征要素為聚類分析的參數,在聚類分析中,需將參數進行賦值,以計算各測試用例之間的距離。考慮到本文只針對名義變量,規定相同變量間距離為0,不同變量間距離為1。其中,對于幾乎靜止的要素如天氣等,可將其設置為較小的值。基于上述方法得到的聚類結果如表4、表5所示。
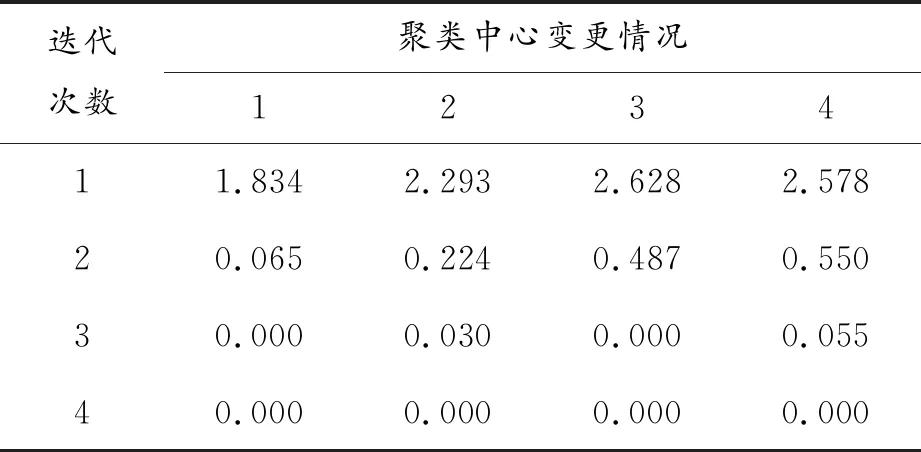
表4 迭代記錄
根據表4可得,當進行第4次迭代時,各個聚類中心的絕對坐標不再改變。因此,本文最終的聚類個數為4。根據SPSS得到的結果,查閱要素編碼表,最終得到4種危險典型場景,如表5所示。

表5 4種危險典型場景
3 前車車速預測模型
本文基于采集的實車數據作為樣本,利用馬爾科夫模型和循環神經網絡分別對平穩工況和快變工況下前車車速進行預測。
3.1 前車狀態數據采集
本文以某公司生產的自動駕駛巴士為測試車輛,車上裝載多線激光雷達和毫米波雷達,底盤采用CAN總線進行通訊,對實際道路工況進行采集。由于實際道路采集的數據受周圍環境、道路結構、駕駛風格等因素影響,因此需要對數據進行處理。其中采集的數據集包括前車速度、前車加速度等數據。為建立符合我國交通特征的跟車工況,根據以下準則篩選出相應數據[7]。
1) 考慮到換道、超車情況,前后兩車距離應滿足|Δdi|<8 m,其中Δdi為主車與前車之間的距離,單位為m。
2) 為確保跟車安全,兩車速度差應滿足|Δvi|<5 km/h,其中Δvi為主車與前車速度之差。
3) 連續跟車大于10 s時,不考慮起步、停車過程。
根據上述準則篩選出車輛跟車數據,其中前車速度、加速度概率分布情況如圖3、圖4所示。
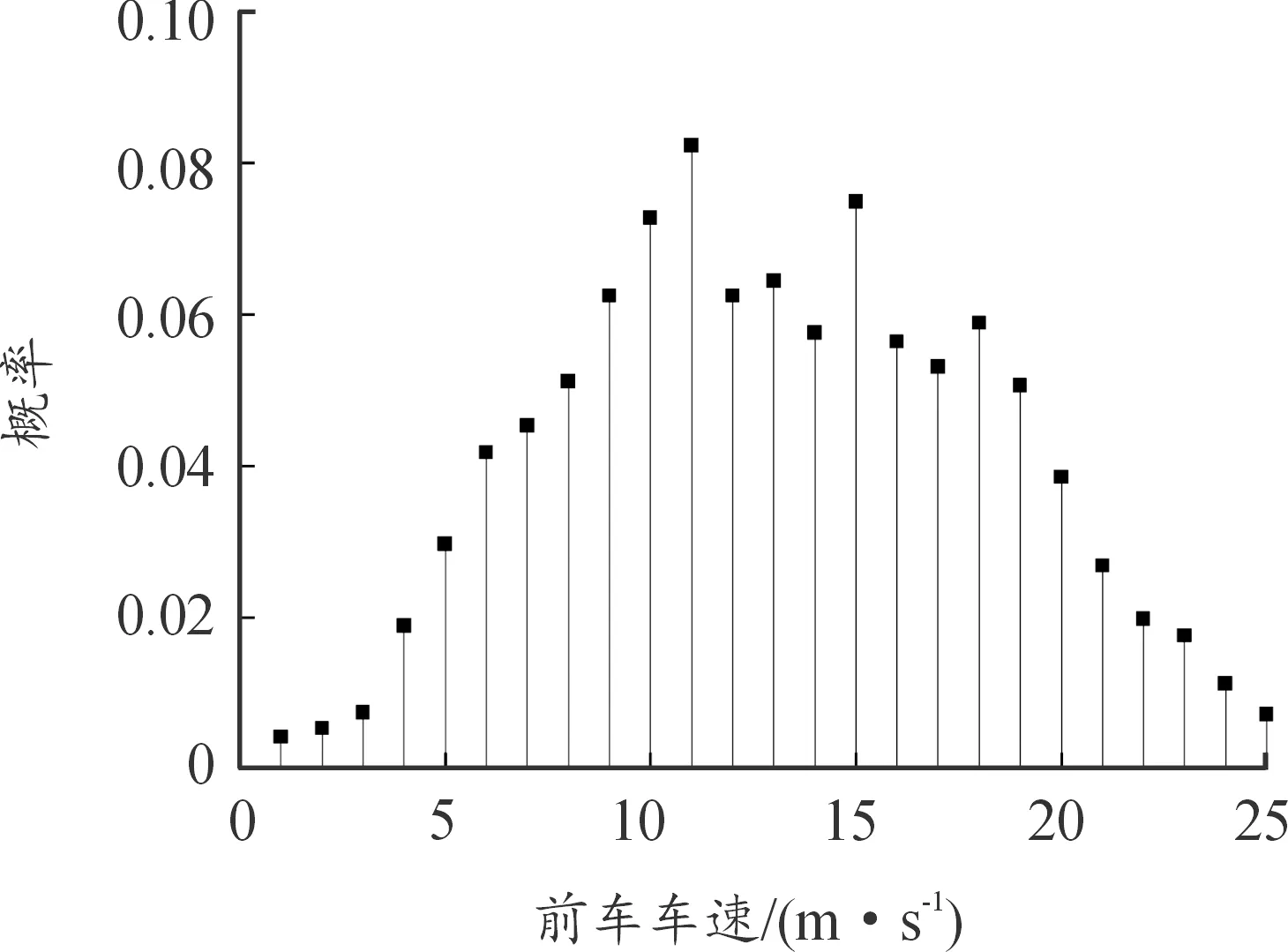
圖3 前車速度概率分布
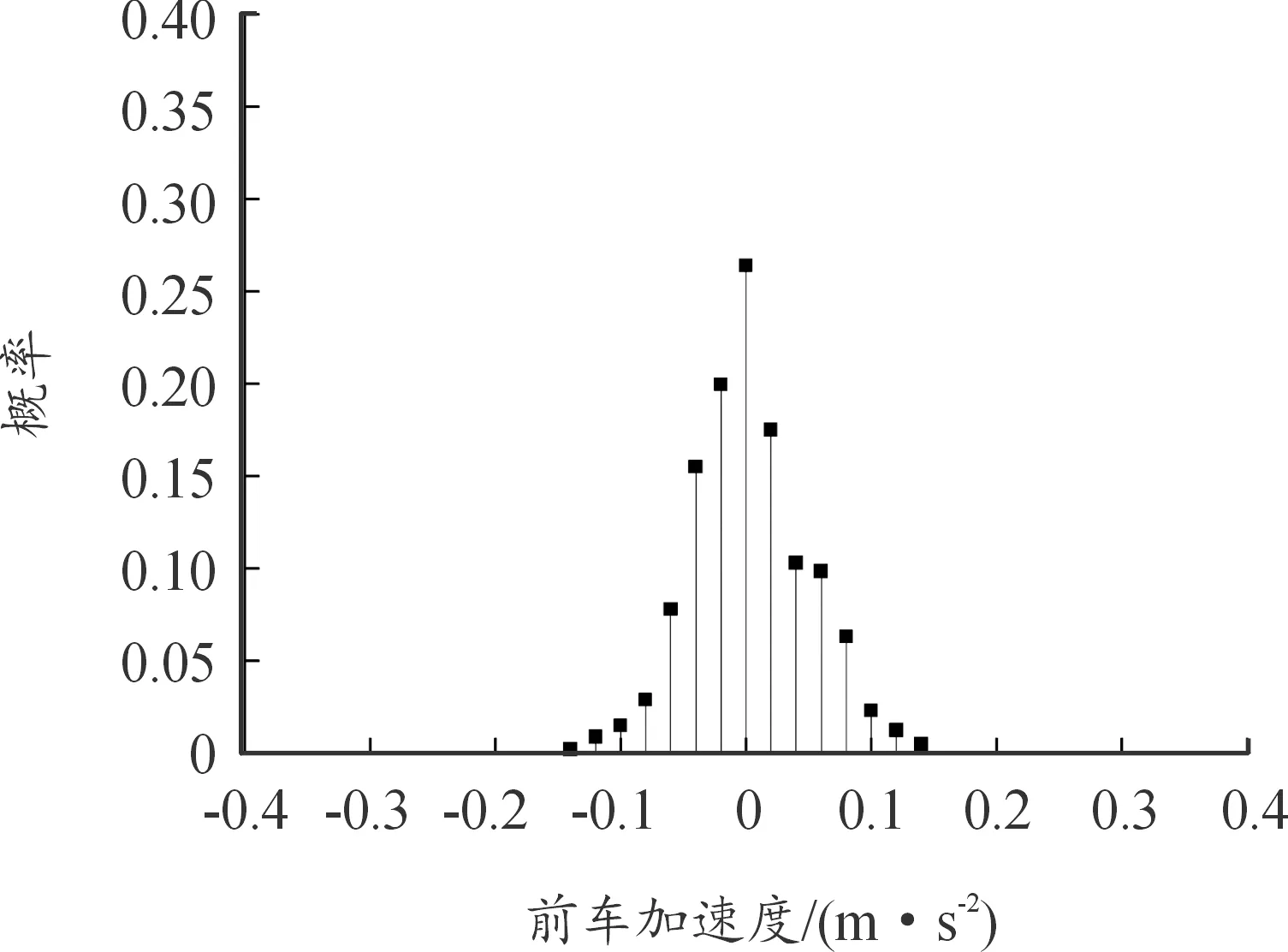
圖4 前車加速度概率分布
3.2 平穩工況下預測模型構建
為準確預測前車運動狀態,參照文獻[14]的工況判斷方法,將篩選出的工況分為平穩工況和快變工況。以采集的數據為基礎,在平穩工況下構建基于馬爾科夫的前車狀態預測模型。假設車輛未來的狀態與歷史狀態無關,則當前車輛的狀態變化可視為一種馬爾科夫過程。假設駕駛過程為隨機過程ω,ω(m)為m時刻前車的狀態,其中ω(m)可以表示速度、加速度等參數的隨機組合。根據條件概率定義,由狀態sm轉移到sn的轉移概率可定義為:
Tmn={X(t+1)=sm|X(t)=sn}
(12)
式中:Tmn為t時刻的轉移概率,即從t時刻sm轉移到t+1時刻sn的概率。將歷史數據劃分為若干片段,隨機組成不同狀態并依次編碼。車輛運行時,狀態間隨機進行轉換,可根據這一屬性和歷史數據得到狀態轉移矩陣,公式如下:
(13)
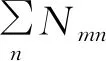
(14)
式中:vm為下一時刻車速;vn為當前車速;aj(m)為下一時刻加速度。根據單次試驗時的數據,可得到馬爾科夫鏈轉移概率矩陣元素,如圖5所示。
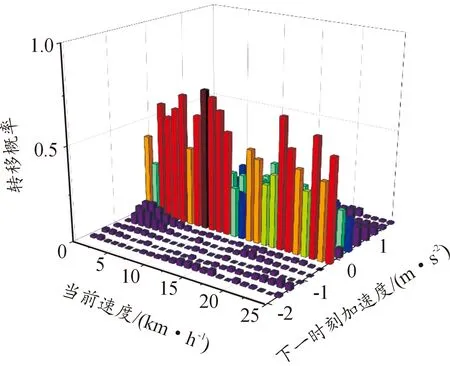
圖5 馬爾科夫模型轉移矩陣元素
3.3 快變工況下預測模型構建
考慮到馬爾科夫預測模型在前車工況波動較大時預測魯棒性較弱,不能實時為主車提供準確的前車運行狀態。因此,本文采用循環神經網絡(recurrent neural network,RNN)對前車多變工況進行預測,通過對駕駛行為序列的自學習預測前車狀態[16]。
循環神經網絡具有深度神經網絡的輸入、輸出和隱藏層,且隱藏層具有傳統神經網絡的前饋連接,并且每個神經元都具有自反饋功能,RNN模型如圖6所示。

圖6 RNN模型示意圖
其中,定義RNN模型的輸入層xt(n)為歷史車速和加速度信息,輸出層yt為前車未來車速和及加速度,隱藏層采用具有自反饋功能的偏執向量。
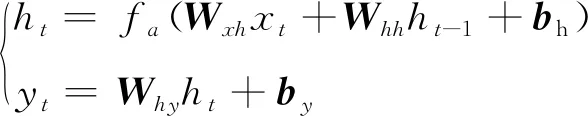
(15)
式中:W為權重系數矩陣(Wxh表示輸入層到隱藏層的權重系數);b為偏置向量(bh表示隱藏層的偏置向量);fa為激活函數,t為當前時刻。其中損失函數為:
(16)
式中:pi和yi分別為前車車速預測值和真實值;(m-l,l)為輸出結果的維度。設定損失函數最小為優化目標。RNN模型根據輸入的歷史車速和加速度信息預測未來車速,根據相應的誤差項和權重梯度實現循環神經網絡在線學習。
4 仿真驗證與分析
為驗證前文中車速預測模型和測試場景生成方法的有效性,在Prescan和Matlab/Simulink中搭建聯合仿真平臺。車輛模型選用Prescan自帶車型,在Prescan界面中對車輛、場景參數、輸入輸出進行配置,通過界面可實時觀察仿真結果。圖7為部分三維仿真場景。定位系統和傳感器融合策略在Matlab/Simulink中搭建,設置采樣時間間隔為0.1 s。考慮到自車車速的危險工況多在20~40 km/h,將測試車輛采集的數據作為樣本數據,統計可得目標車加速度呈近似正態分布。

圖7 部分三維仿真場景
將聚類的4種場景中自車車速作為歷史數據,可得城市場景、二級公路場景、三級公路場景的速度,如圖8所示。3種場景中的速度誤差集中在 2 km/h范圍內,考慮到原始工況下車輛隨機性及環境隨機性較大,通過對采集數據的學習得到預測模型,結果存在一定的差異,其中體現了車輛狀態的隨機性。城市場景車輛頻繁啟停,速度誤差波動較大,二級公路、三級公路波動較小。
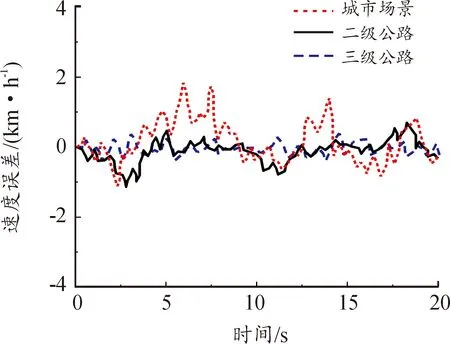
圖8 3種場景預測速度誤差
5 試驗驗證與分析
為進一步驗證前文提出的前車車速預測模型的準確性,利用某公司生產的自動駕駛套件標定系統將模型參數導入至整車控制器中,進行實驗驗證。試驗小車如圖9所示。

圖9 試驗小車
5.1 試驗小車通訊方式
全車采用基于CAN卡的通訊方式,協議采用主從通訊模式,主設備是測量標定系統,從設備是整車控制器。當主從設備建立聯系后,主設備控制所有通訊數據,從設備接受數據并反饋代碼信息和報文。
5.2 試驗
在實車試驗前,啟動Dreamview平臺,并在Cyber monitor里查看小車定位、感知、預測等通道的信號是否正常。試驗時小車安全車速為20~30 km/h,最大加速度為5 m/s2。實車測試表明:在試驗條件下,預測模型能平均提前4.86 s預測前車車速,且單程誤差率小于0.1%,誤差較小且實用價值較高。分別對試驗后速度指標和加速度指標進行分析,試驗與仿真場景如圖10—12所示。通過觀察3種場景下前車速度和加速度的試驗與仿真對比圖,其變化趨勢基本一致。部分片段偏差過大,這種現象是由試驗環境及測量誤差造成的,均在合理范圍之內。
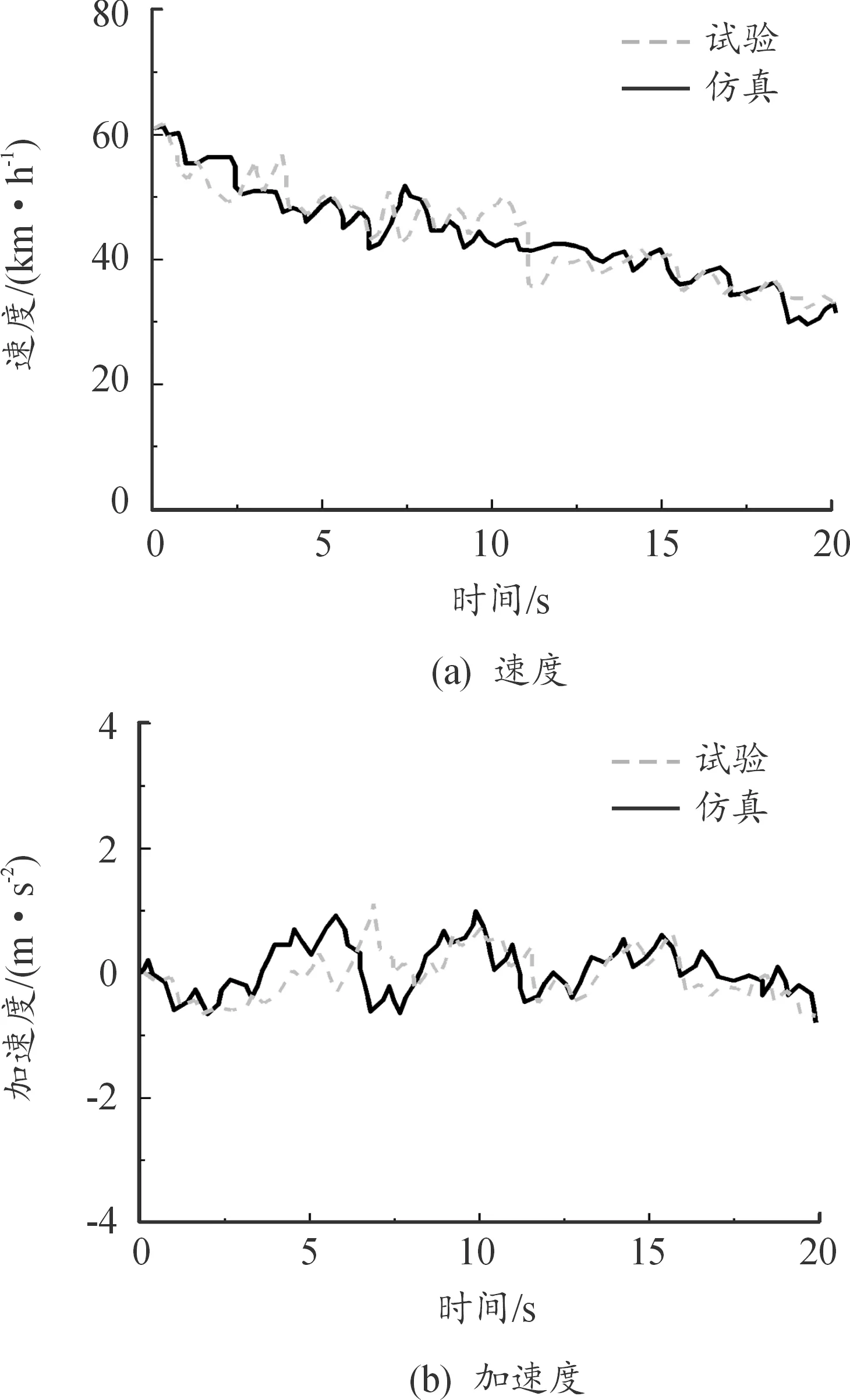
圖10 城市場景試驗與仿真
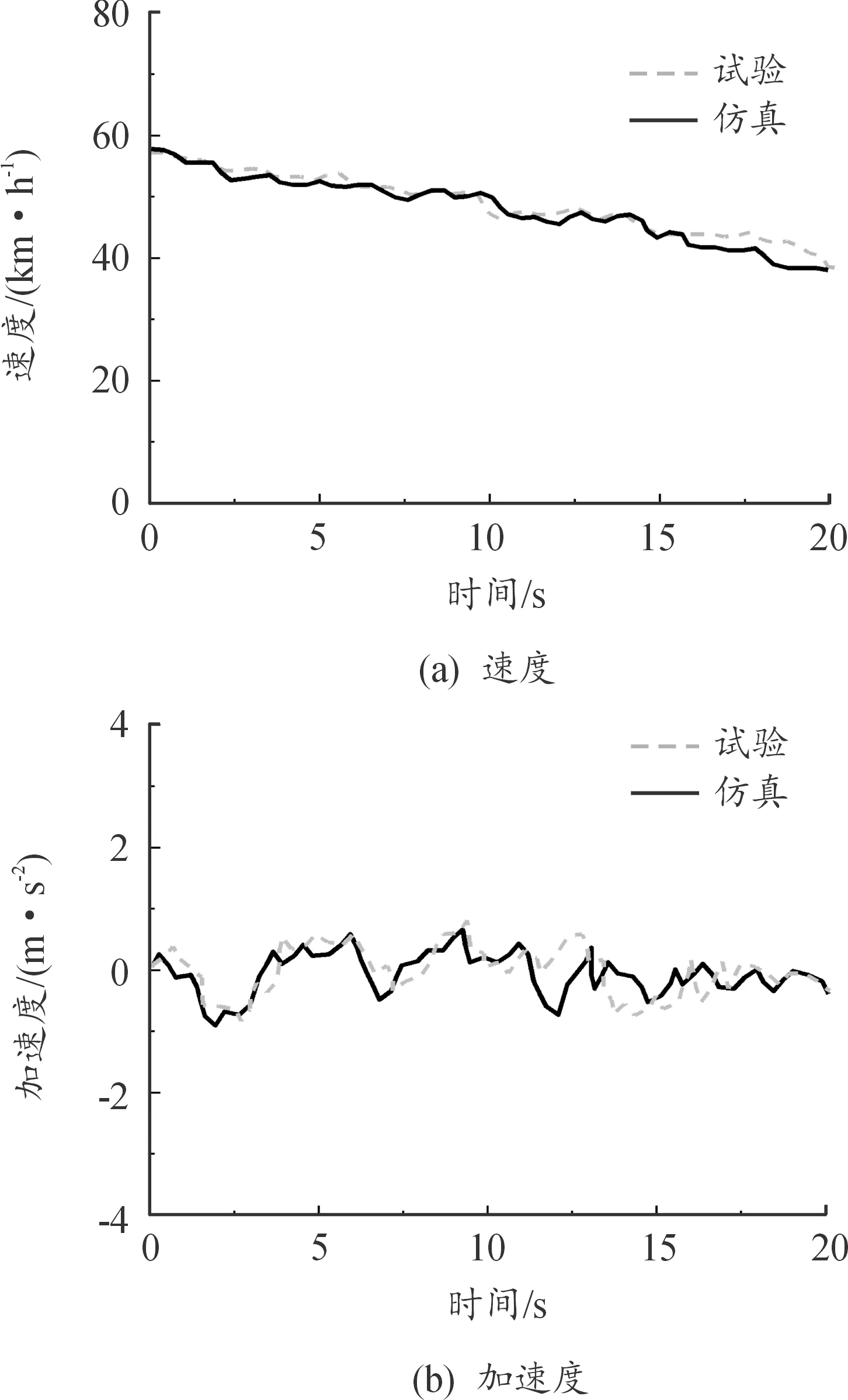
圖11 二級公路場景試驗與仿真
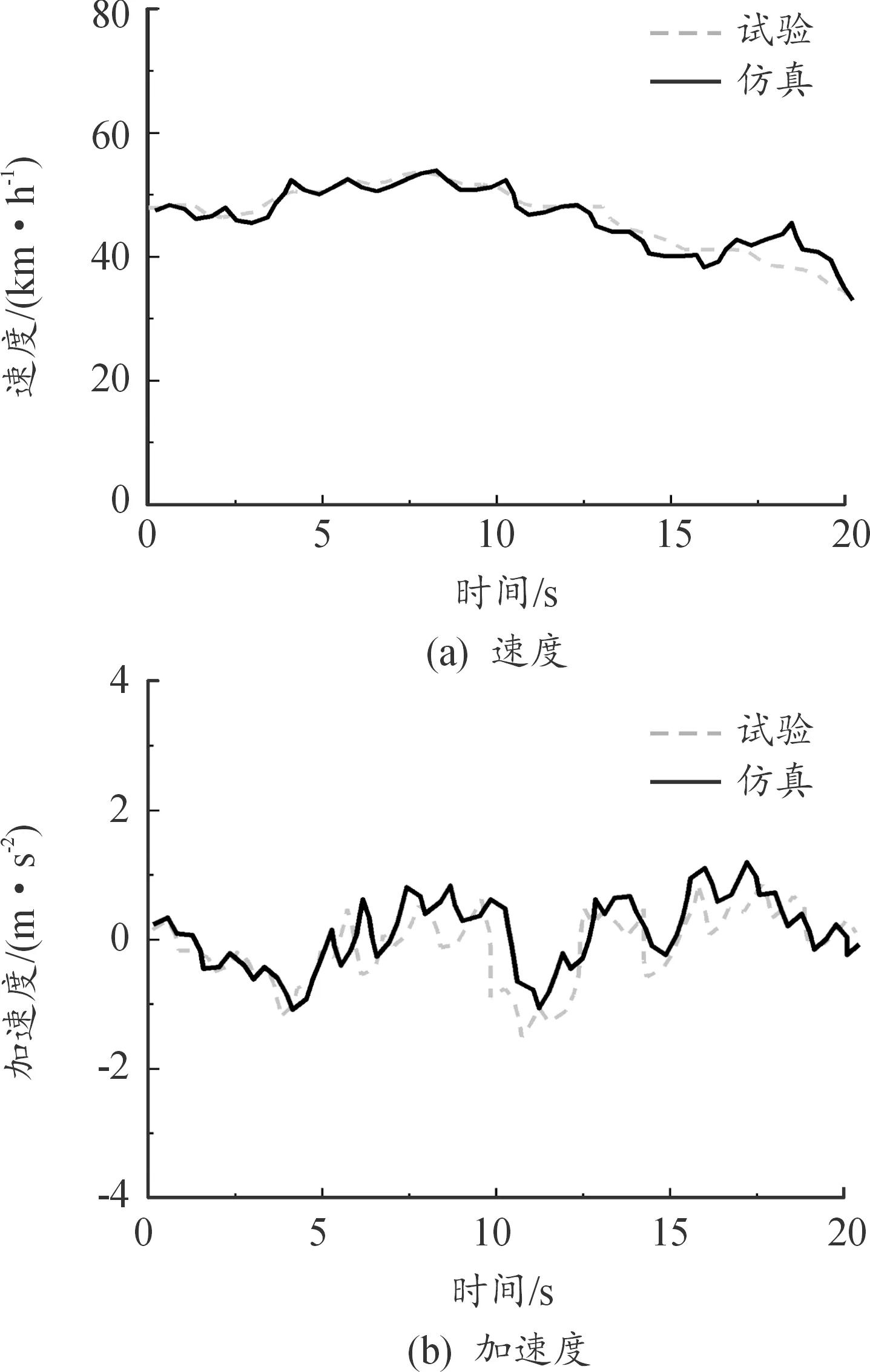
圖12 三級公路場景仿真與試驗
根據表6可以看出,城市場景和二級公路場景誤差車速較小,三級公路場景誤差車速較大,這是因為試驗條件和測試誤差造成的。由此可以看出,所構建的車速預測模型能較好地預測前車車速,實車試驗驗證了預測模型仿真系統的有效性。
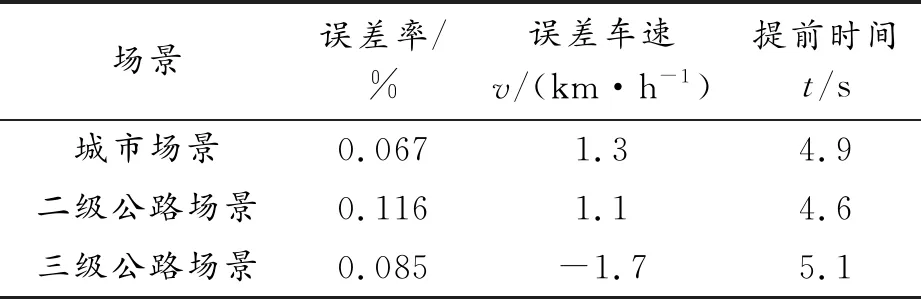
表6 預測試驗結果
6 結論
1) 基于NAIS數據庫,在置信區間為95%時,在構建的多元線性回歸模型中提取得到4個特征要素,對特征要素使用K均值聚類算法,挖掘出4種危險典型場景。
2) 基于實際跟車數據,分別對平穩工況和快變工況建立馬爾科夫和循環神經網絡車速預測模型。基于Prescan、Simulink聯合仿真平臺,對典型場景下車速預測模型進行驗證,仿真結果表明:所提出模型的車速預測誤差小于2 km/h,在合理范圍內。
3) 基于馬爾科夫模型和循環神經網絡模型平均能提前4.86 s預測前車車速,且單程誤差小于0.1%,實用性較高。未來的工作是探究如何快速生成典型測試場景。

