提升空間中漸近平均跟蹤性和鏈回歸點的研究
冀占江,貝彩霞,張更容
(1.梧州學院大數據與軟件工程學院,廣西高校圖像處理與智能信息系統重點實驗室,廣西高校行業軟件技術重點實驗室,廣西 梧州 543002;2.梧州職業學院衛生健康學院,廣西 梧州 543002;3.湖南第一師范學院數學與計算科學學院,湖南 長沙 410205)
0 引言
研究n維環面等特殊流形上動力學性質時最常用的方法就是提升系統,因此一個系統與它的提升系統的動力學性質是否一致就成為研究的熱點[13-14].考慮到漸近平均跟蹤性和鏈回歸點具有較高的應用價值且它們在提升空間中的研究成果較少,本文選擇在提升空間中研究它們的動力學性質,所得結論彌補了提升空間中漸近平均跟蹤性和鏈回歸點理論的缺失.
1 預備知識
定義1 設X,Y是拓撲空間.稱f是一個同胚映射,如果f:X→Y是一一映射且f和f-1都是連續的.
定義2[15]設(X,d1)和(Y,d2)是度量空間,f:X→Y是一一映射.稱f是等距映射,如果對任意的x,y∈X,有d2(f(x),f(y))=d1(x,y).
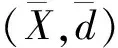
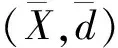
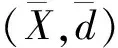
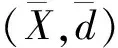
定義7[16]設J?N.稱J是密度零集,如果
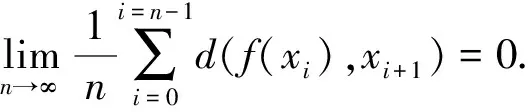
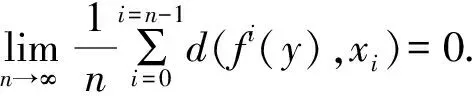
定義10 設(X,d)是度量空間,f:X→X連續.稱f具有漸近平均跟蹤性,如果{xi}i≥0是X中f的任意漸近平均偽軌,存在y∈X使得y漸近平均跟蹤{xi}i≥0.
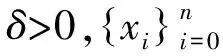
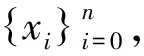
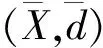

是等距同胚映射.
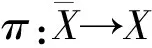
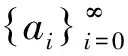
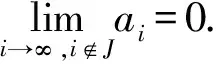
2 主要定理及證明
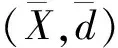

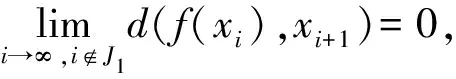
d(f(xi),xi+1)<ε.
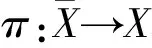
再由引理1可知,
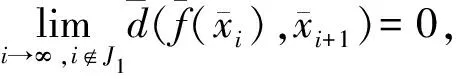
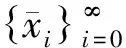
由引理2知,存在密度零集J2使
故?N2∈N+,當i≥N2且i?J2時,有
(1)
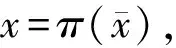
是等距映射,故
根據(1)式,當i≥N2且i?J2時,有
d(fi(x),xi)<ε.
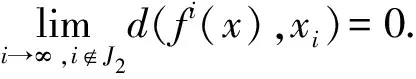
則f具有漸近平均跟蹤性.
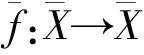
(2)
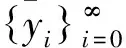
由引理2,存在密度零集J3使
故?N3∈+,當i≥N3且i?J3時,有
(3)
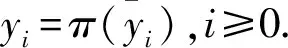
由(3)式,當i≥N3且i?J3時,有
d(f(yi),yi+1)<η.
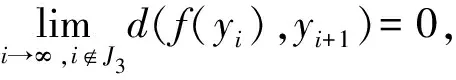
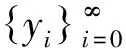
d(fi(y),yi)<η.
(4)
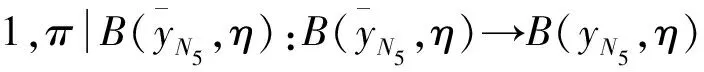
由(4)式可知,
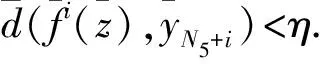
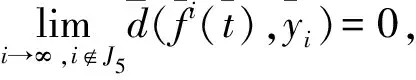
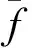
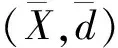
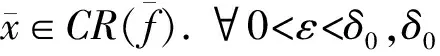
(5)
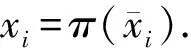
是等距映射,故
由(5)式有
d(f(xi),xi+1)<ε.
3 總結


