MATLAB在線性時不變系統(tǒng)時域求解中的應用

安成錦，楊俊剛，王雪瑩，吳 京

（國防科技大學電子科學學院，湖南 長沙 410073）

0 引言

系統(tǒng)的時域分析是指在給定的激勵作用下，通過不同的數(shù)學方法求解系統(tǒng)的響應。為了確定線性時不變系統(tǒng)對給定激勵的響應，需要建立描述該系統(tǒng)的方程，并給出一定的初始狀態(tài)。如果把對系統(tǒng)的定性和定量分析限定在時域內(nèi)，這就是系統(tǒng)的時域分析法[1]。

利用手工求解方程，尤其是高階方程有一定的難度。將MATLAB引入到信號與系統(tǒng)分析中，把常用的求解方法編寫成MATLAB代碼，供求解實際問題時直接使用。既可以避免煩瑣的數(shù)學運算，簡化問題的求解過程，又可以實現(xiàn)分析結果的可視化[2]。

但目前“信號與系統(tǒng)”方面的書籍，要么沒有介紹系統(tǒng)求解的MATLAB實現(xiàn)[3][4]，要么僅介紹了零輸入響應求解，缺少完整的連續(xù)、離散系統(tǒng)的零輸入、零狀態(tài)響應MATLAB求解方法[5][6]。本文首先介紹了利用MATLAB從時域求解連續(xù)系統(tǒng)的方法，接著介紹了求解離散系統(tǒng)的方法，最后對結果進行了一定的分析。

1 連續(xù)時間線性時不變系統(tǒng)零狀態(tài)響應求解實例

連續(xù)時間系統(tǒng)的數(shù)值求解在MATLAB中可利用控制系統(tǒng)工具箱中的lsim函數(shù)，調用形式為：

lsim(sys,u,t,x0)

其中sys是系統(tǒng)的表示，向量u和t分別表示輸入信號和時間t的抽樣值，向量x0表示系統(tǒng)的初始狀態(tài)，缺省值為0，返回值為系統(tǒng)的輸出。如果調用lsim(sys,u,t)，得到的結果即為系統(tǒng)的零狀態(tài)響應。

解：MATLAB源代碼如下，程序運行結果如圖1所示。

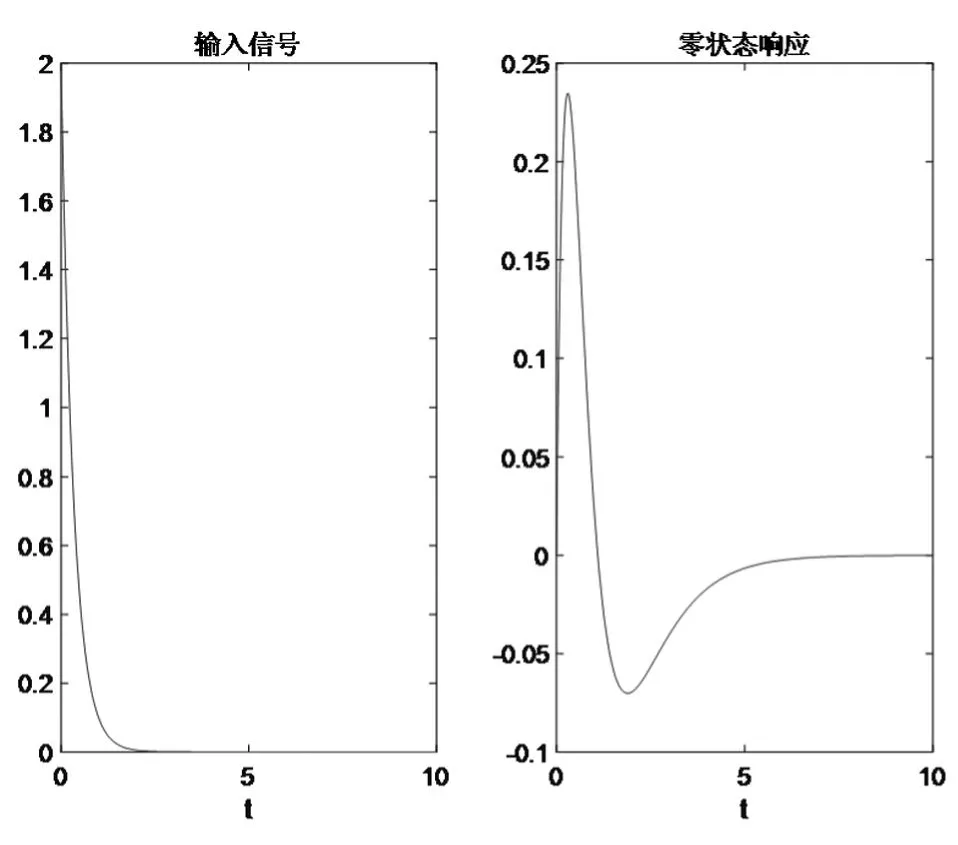
圖1 連續(xù)時間系統(tǒng)的零狀態(tài)響應

2 連續(xù)時間線性時不變系統(tǒng)零輸入響應求解實例

通常認為將lsim函數(shù)的輸入信號置零，再將初始狀態(tài)代入x0，則可得到連續(xù)時間系統(tǒng)的零輸入響應。但事實上lsim函數(shù)只能對狀態(tài)方程描述的系統(tǒng)計算零輸入響應，對前面得到的輸入-輸出系統(tǒng)的表示失效[7]。雖然在MATLAB中沒有專門的函數(shù)求解連續(xù)時間系統(tǒng)零輸入響應的數(shù)值解，但可利用dsolve函數(shù)得出解析解。調用形式為：

S=dsolve(eqn,cond)

其中eqn為方程，cond為初始條件。

解：MATLAB源代碼如下，程序運行結果如圖2所示。

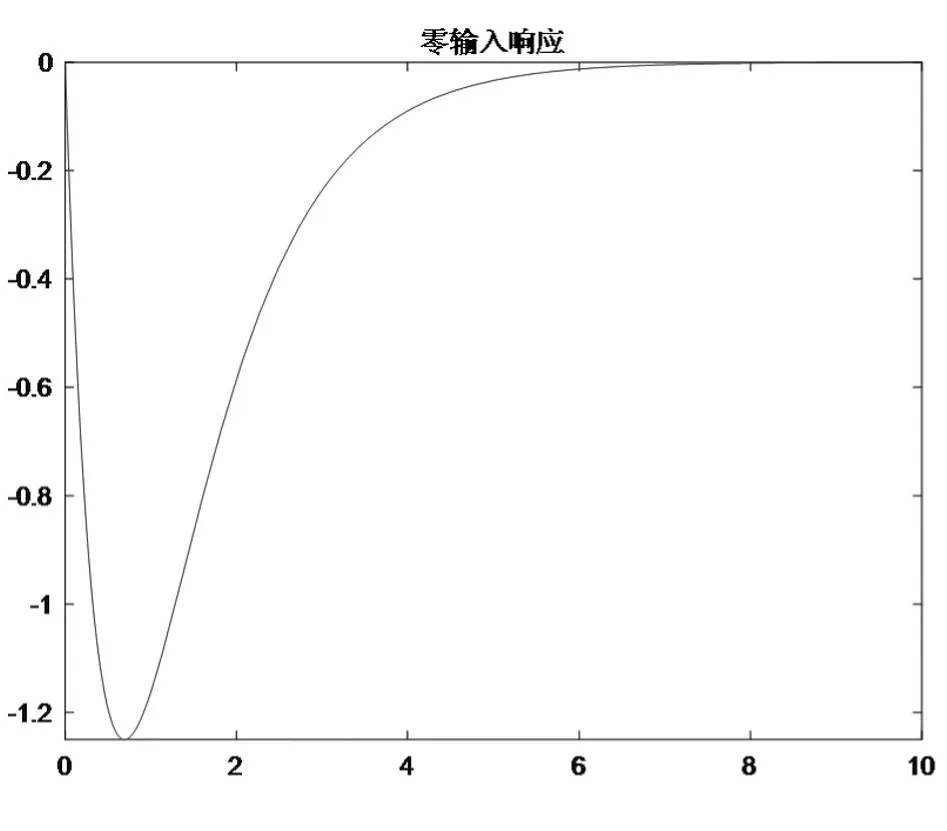
圖2 連續(xù)時間系統(tǒng)的零輸入響應

3 離散時間線性時不變系統(tǒng)零狀態(tài)響應求解實例

大部分離散時間線性時不變系統(tǒng)可以用常系數(shù)線性差分方程表示：

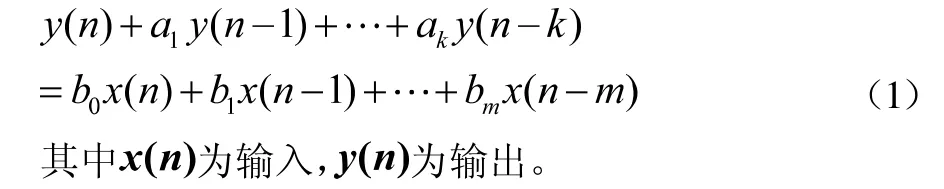
離散時間系統(tǒng)的數(shù)值求解在MATLAB中可利用信號處理工具箱中的filter函數(shù)，調用形式為：

y=filter(b,a,x,zi)

解：MATLAB源代碼如下，程序運行結果如3所示。觀察發(fā)現(xiàn)，輸入有界時，零狀態(tài)響應發(fā)散，該系統(tǒng)為不穩(wěn)定系統(tǒng)。

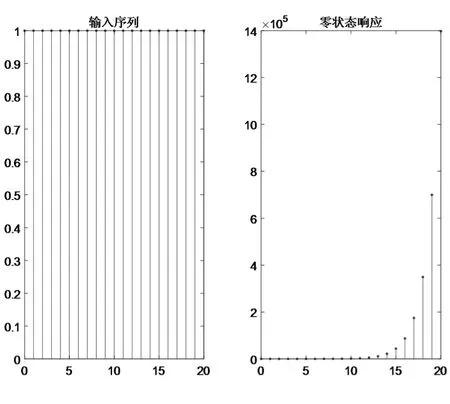
圖3 離散時間系統(tǒng)的零狀態(tài)響應

4 離散時間線性時不變系統(tǒng)零輸入響應求解實例

通常認為將filter函數(shù)的輸入信號置零，再將初始狀態(tài)代入x0，則可得到離散時間系統(tǒng)的零輸入響應。但與連續(xù)時間系統(tǒng)的lsim函數(shù)類似，filter函數(shù)只能對狀態(tài)方程描述的系統(tǒng)計算計算零輸入響應。在MATLAB中，有專門的函數(shù)將初始狀態(tài)由傳遞函數(shù)描述的系統(tǒng)轉換成狀態(tài)方程描述的系統(tǒng)，調用形式為：

z=filtic(b,a,y,x)

其中b、a還是輸入、輸出信號的系數(shù)向量；y表示輸出；x表示輸入，缺省值為0；z表示狀態(tài)方程的初始狀態(tài)。

得到z后，再將其代入filter函數(shù)，并令輸入為零，即可得到系統(tǒng)的零輸入響應。

解：MATLAB源代碼如下，程序運行結果如圖4所示。

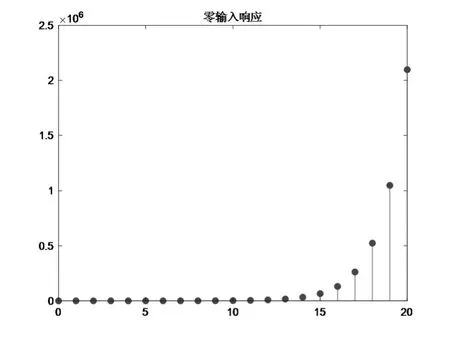
圖4 離散時間系統(tǒng)的零輸入響應

5 離散時間線性時不變系統(tǒng)全響應求解實例

對于離散時間系統(tǒng)全響應求解，可以利用filter函數(shù)，代入輸入序列和初始狀態(tài)直接得出；也可以將差分方程進行一定的整理，將輸出y(n)單獨放在等號一邊，對于例4，即為，然后編程迭代得到。

解：MATLAB源代碼如下，程序運行結果如圖5所示，比較發(fā)現(xiàn)兩種方法得到的全響應相等。

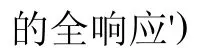
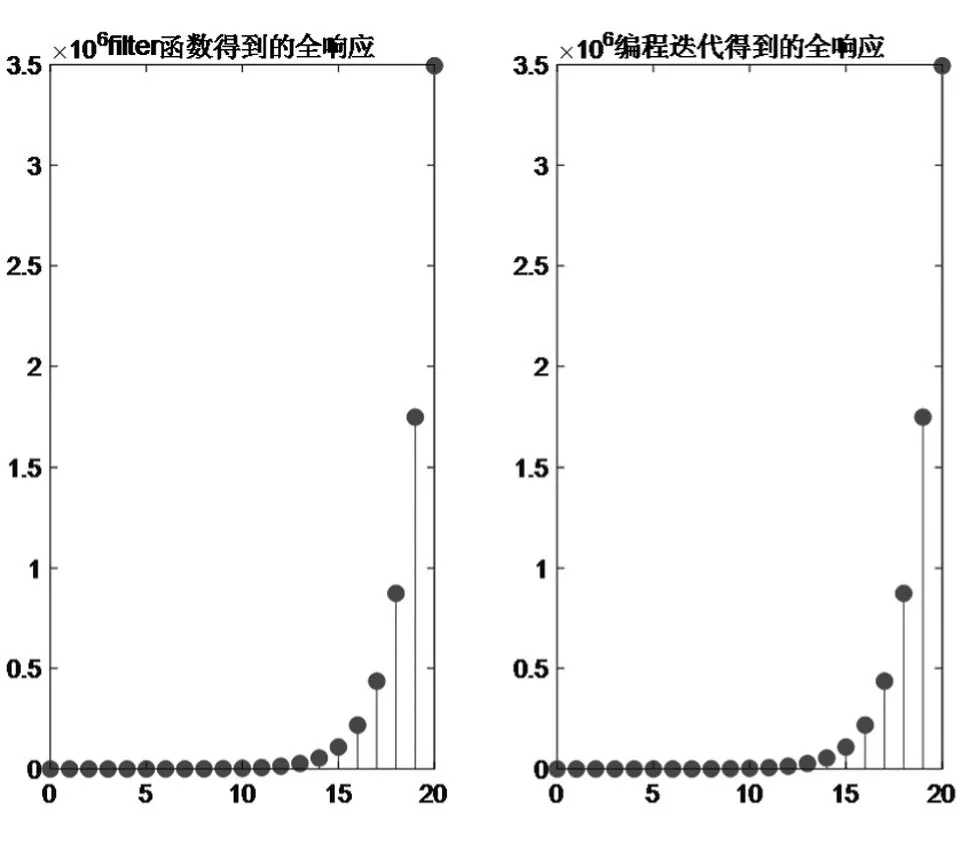
圖5 兩種方法得到的離散時間系統(tǒng)全響應

6 結語

結果表明，MATLAB的數(shù)值計算和符號計算功能可使線性時不變系統(tǒng)的響應求解過程大大簡化，并能得到可視化效果。文章涉及的是系統(tǒng)時域求解問題，事實上，MATLAB在頻域、復頻域、Z域分析和求解中也得到了廣泛的運用。