一類長記憶時間序列趨勢項變點的Wilcoxon秩檢驗
成守堯,陳占壽*,娘毛措,汪肖陽
(1.青海師范大學數學與統計學院,青海 西寧 810008;2.藏語智能信息處理及應用國家重點實驗室,青海 西寧 810008)
變點是指隨機序列或過程中的某個位置或時刻,變點前、后的觀測值或數據服從不同的模型。變點問題早期應用于工業質量控制,后在其他領域中有所發展,如金融、經濟、計算機、氣象學、流行病學等,引起廣泛關注。近年來,各種統計模型中的變點問題得到了較為深入的研究,主要變點類型有均值變點、方差變點、趨勢項變點等。本文主要研究時間序列模型趨勢項變點的檢驗問題,其早期研究可參見文獻[1]。HU?KOVá等[2]基于極大似然方法構造了檢驗趨勢項變點的統計量,并采用Bootstrap方法近似計算了統計量的臨界值。秦瑞兵等[3]基于最小二乘估計殘差構造了累積和(cumulative sum,CUSUM)型統計量檢驗趨勢項變點。JIANG等[4]提出了同時檢驗和估計趨勢項變點的SN-NOT方法,將自正則化方法與NOT算法[5]相結合,不僅顯著提升了檢驗效率和估計精度,而且將其成功應用于多個國家新冠病毒感染確診人數趨勢變化分析。TAN等[6]提出了一種基于加權經驗特征函數的方法,將其用于估計分布函數變點,并提出了一種參數自適應驅動選擇方法,以選取合適的參數。上述均在獨立或短記憶模型的假設下研究變點,而有關長記憶時間序列模型變點的研究較少。
分數布朗運動[7]具有長記憶性,其長記憶性由Hurst指數刻畫。分數布朗運動可近似擬合具有長記憶性的數據,如水文數據、金融數據等,故其在水文[8]、金融[9-10]等領域應用廣泛。WENGER 等[11]提出了固定帶寬的CUSUM檢驗并將其用于長記憶時間序列均值變點。長記憶時間序列模型變點檢驗方法與最新研究成果可參見文獻[12]。基于Wilcoxon 秩檢驗方法的穩健性,WANG[13]研究了長記憶時間序列模型分布函數變點的檢驗問題,DEHLING等[14]提出了檢驗長記憶時間序列均值變點的 Wilcoxon秩方法,BETKEN[15]進一步提出了自正則化的Wilcoxon秩方法檢驗長記憶時間序列均值變點,由于自正則化方法避免了長期方差估計,在使用時更簡便。WENGER等[16]通過改進長期方差的估計提出了一種修正的Wilcoxon秩檢驗方法。
本文先對觀測序列做一階差分,再基于差分序列構造Wilcoxon秩統計量,以檢驗分數布朗運動趨勢項變點,在原假設下推導檢驗統計量的極限分布,并用數值模擬方法得到檢驗統計量的臨界值。模擬結果表明,除Hurst指數較大情況外,給出的臨界值均能很好地控制經驗水平,且經驗勢隨樣本量的增大逐漸趨近于1,說明本文提出的檢驗分數布朗運動趨勢項變點的統計量是一致統計量。此外,模擬研究發現,當樣本量較大時,本文方法對截距項變點和方差變點是穩健的,即當趨勢項不存在變點時,截距項變點和方差變點對檢驗幾乎無影響,經驗水平仍接近檢驗水平;當趨勢項存在變點時,截距項變點對經驗勢的影響很小,而當樣本量較小時,經驗勢隨方差變點的增加而降低,但隨樣本量的增多,經驗勢仍可趨于1。這意味著用本文方法做趨勢項變點檢驗時,當數據中不存在趨勢項變點但存在截距項或方差變點時,不會拒絕不存在趨勢項變點的原假設,而當數據中存在趨勢項變點時,不論是否存在截距項或方差變點,只要樣本量足夠大均能檢測到趨勢項變點。在實例分析中,對1854—1989年北半球經季節調整后的1632個月均氣溫數據進行了分析,檢驗結果表明,數據中不存在趨勢項變點,這進一步驗證了已有研究結論。
1 模型與主要結果



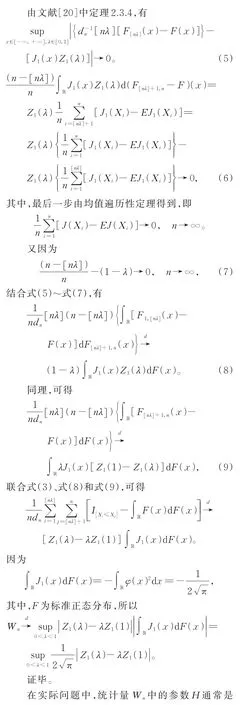

2 數值模擬

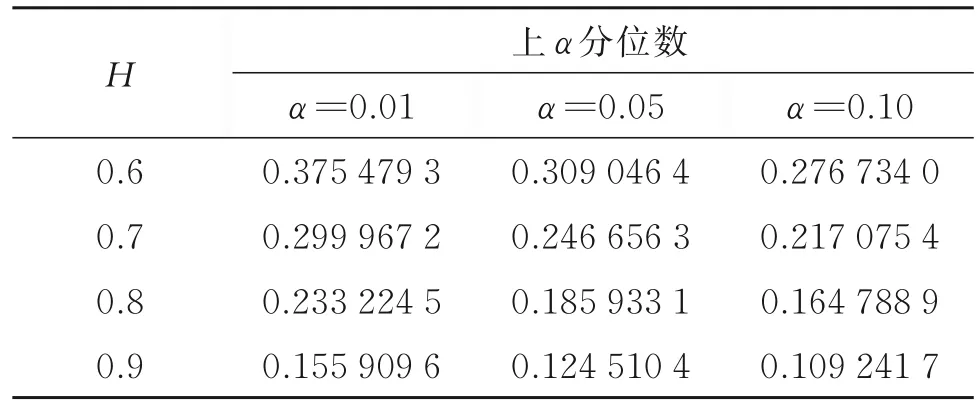
表1 極限分布的上α分位數Table 1 Upper α quantile of the limit distribution
然后,研究統計量W n的有限樣本性質。在式(1)中,由于假設截距項β0t是不變的,不失一般性,假設β0t=0,β1=1,即在無變點原假設下考慮數據:
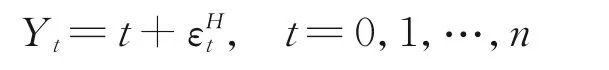
的生成過程。在備擇假設下,數據生成過程為
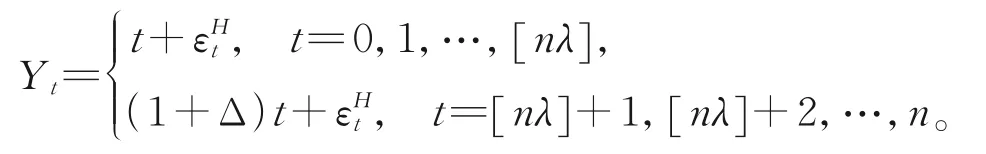
取樣本容量n=50,100,300,500,趨勢項跳躍度Δ=0.05,0.10,考慮變點出現在靠前位置、中間位置、靠后位置3種情況,即取趨勢項變點位置參數λ=0.25,0.50,0.75。表2和表3分別為經驗水平值和經驗勢的模擬結果,所有模擬結果均在α=0.05檢驗水平下經1000次循環得到。
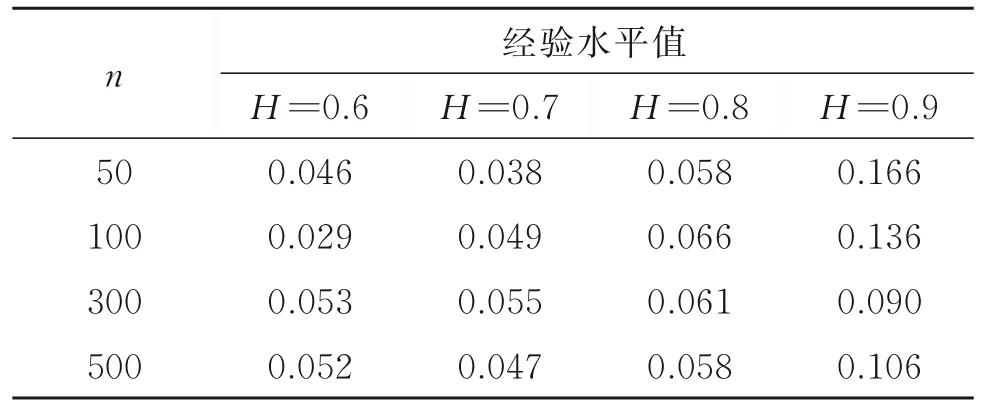
表2 統計量Wn的經驗水平值Table 2 The empirical size of statisticWn
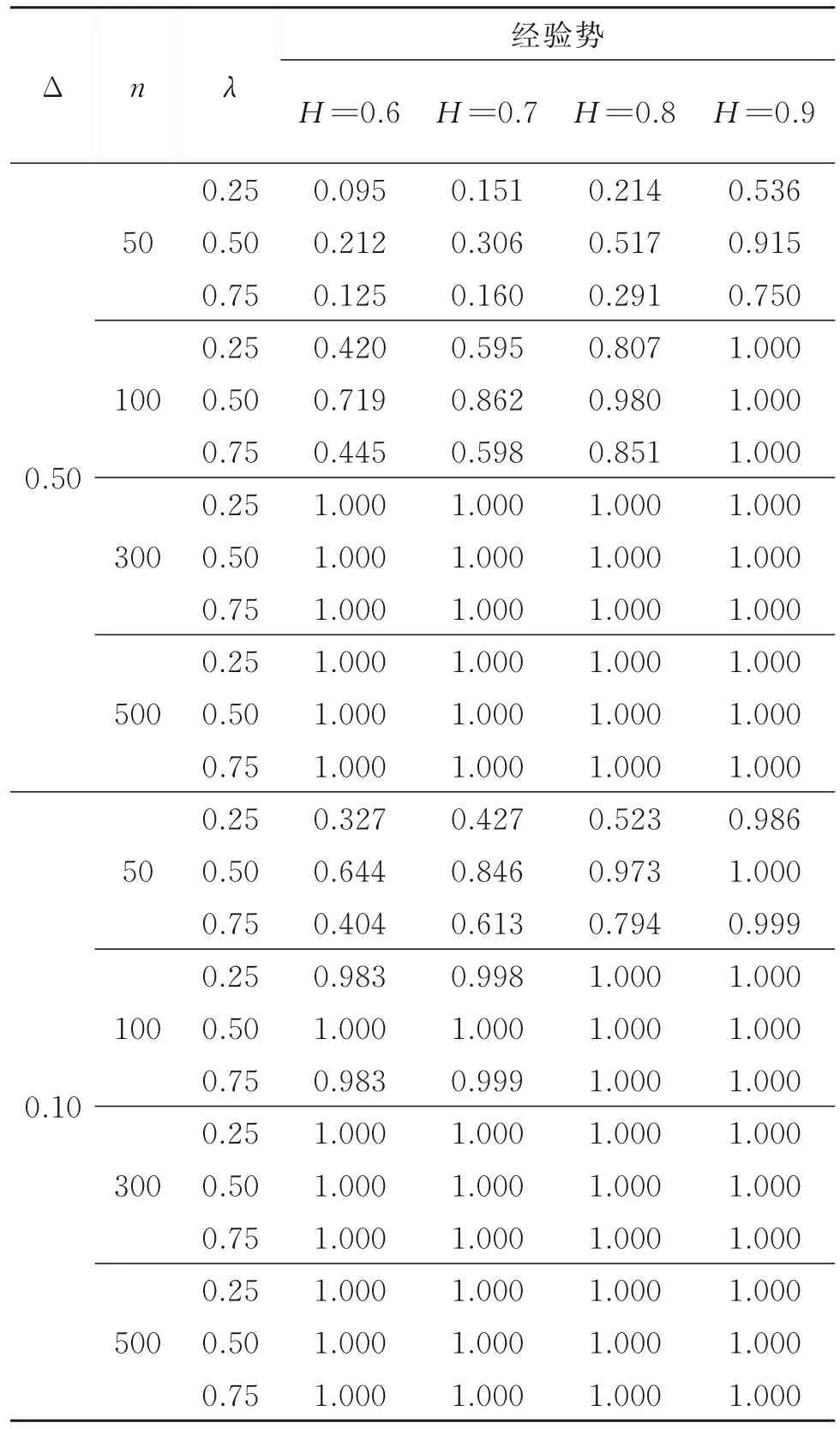
表3 統計量Wn的經驗勢Table 3 The empirical power of statisticWn
由表2知,當Hurst指數較小時,經驗水平值能被較好地控制,且樣本量越大,經驗水平值越接近于0.05,這是因為隨著樣本量的增加,檢驗統計量Wn的經驗分布越接近于其極限分布。然而,當H=0.9時,經驗水平值出現了較明顯的失真,幾乎達α的2倍,這是因為此時數據有很強的長記憶性,需要更大的樣本量才能較好地控制經驗水平。
由表3知,隨著樣本量的增加,經驗勢增大,且除了樣本量較少的情況外,經驗勢幾乎能達到1。這說明統計量Wn是檢驗趨勢項變點的一致統計量。隨著Hurst指數增加,經驗勢也增大。變點出現在中間位置λ=0.50的經驗勢較變點出現在靠前位置λ=0.25或靠后位置λ=0.75的經驗勢大,即變點越靠近中間位置越容易被檢驗到,這符合大部分后驗檢驗統計量的特點。隨著趨勢項跳躍度Δ的增加,經驗勢也隨之增大,這符合直觀邏輯,因為趨勢項跳躍度越大,兩組數據的差異越明顯,越容易檢驗出趨勢項變點。
上述模擬均假設截距項β0t與誤差項的方差是固定不變的,但在實際問題中可能存在截距項變點和誤差項方差變點,此時可通過數值模擬分析截距項變點或誤差項方差變點對檢驗統計量的影響。考慮數據:
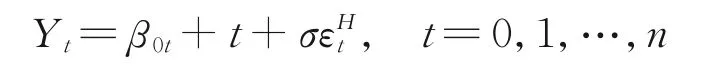
的生成過程。假設截距項β0t在改變前、后的值分別為 0和β0,取β0=0.5,2.0;誤差項的方差變化由σ控制,σ在改變前、后的值分別為1和σ′,取σ′=0.5,2.0。同樣,模擬結果均在α=0.05檢驗水平下經1000次循環得到,進一步假設變點出現在[0.5n]處,討論以下4種情況。
情況1在無趨勢項變點原假設下,β0t在[0.5n]處由 0變為β0;
情況2在無趨勢項變點原假設下,σ在[0.5n]處由 1變為σ′;
情況3在有趨勢項變點備擇假設下,β0t在[0.5n]處由 0變為β0;
情況4在有趨勢項變點備擇假設下,σ在[0.5n]處由 1變為σ′。
由于情況3和情況4假設存在趨勢項變點,因此考慮取趨勢項變點位置參數λ=0.50,趨勢項跳躍度Δ=0.10。
情況1的模擬結果見表4,由表4知,該結果與表2中的模擬結果很接近,說明截距項β0t變點對經驗水平值基本無影響。由于統計量Wn是基于一階差分數據構造的,而截距項變點對一階差分數據的影響僅體現在變點上,因此統計量Wn對截距項變點穩健是預期結果。
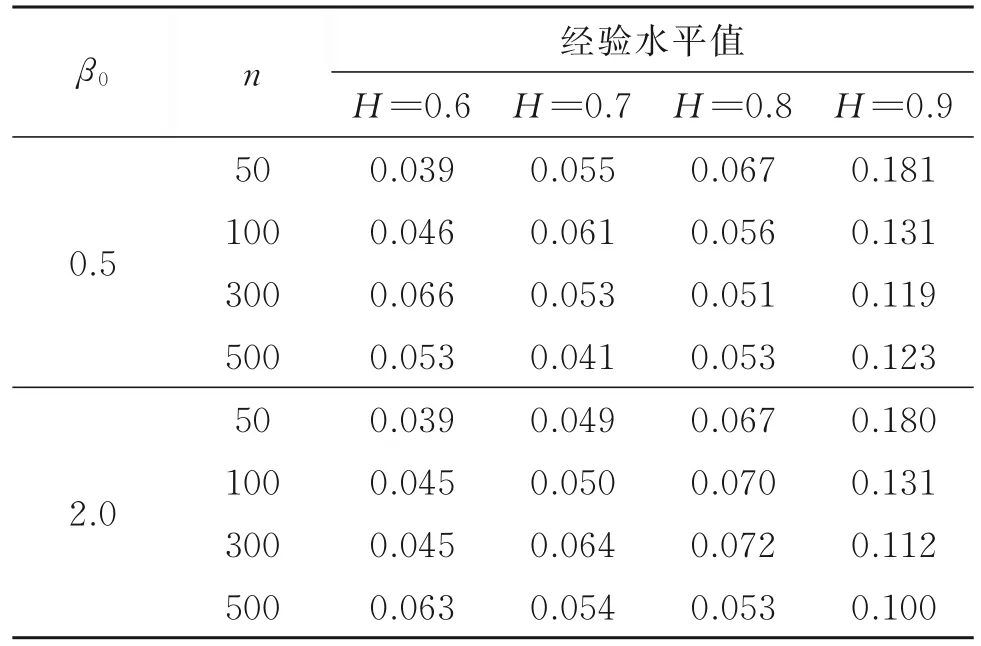
表4 情況1統計量Wn的經驗水平值Table 4 The empirical size of statistic Wnin case 1
情況2的模擬結果見表5,由表5知,當樣本量較大時,σ的改變對經驗水平值的影響較小;當H較大時,σ的改變會使得經驗水平值略微增加,但除了H=0.9的情況外,基本上在可接受范圍內。因此可以認為,在樣本量較大時,本文方法對方差變點也是穩健的。
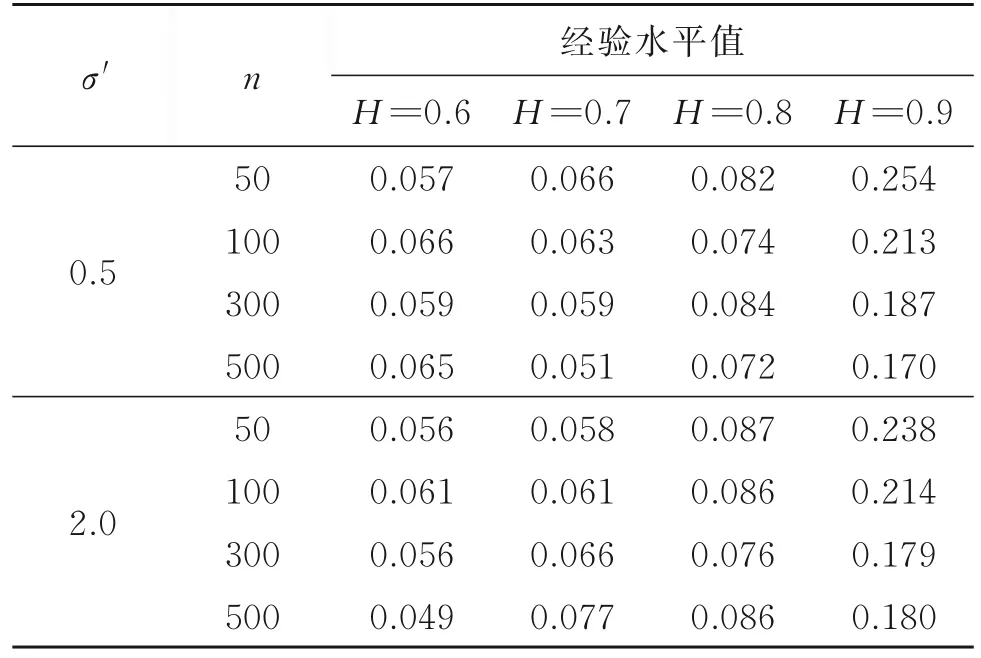
表5 情況2統計量Wn的經驗水平值Table 5 The empirical size of statistic Wnin case 2
由表6知,情況3的模擬結果與表3中Δ=0.10,λ=0.50的模擬結果很接近,表明截距項β0t變點對經驗勢基本無影響。這亦是因為統計量Wn是基于一階差分數據所構造的,而截距項變點對一階差分數據的影響只體現在變點上,所以統計量Wn對截距項變點是穩健的。情況4的模擬結果見表7,由表3中 Δ=0.10,λ=0.50的模擬結果知,當樣本量較小時,隨著方差的增加,經驗勢明顯減小。這是因為方差增加,使得誤差項在數據中的占比增加,導致趨勢項的改變對數據的影響降低。在樣本量足夠大時,經驗勢仍趨于1,因此可以認為,在較大樣本量下,本文方法對方差變點同樣是穩健的。
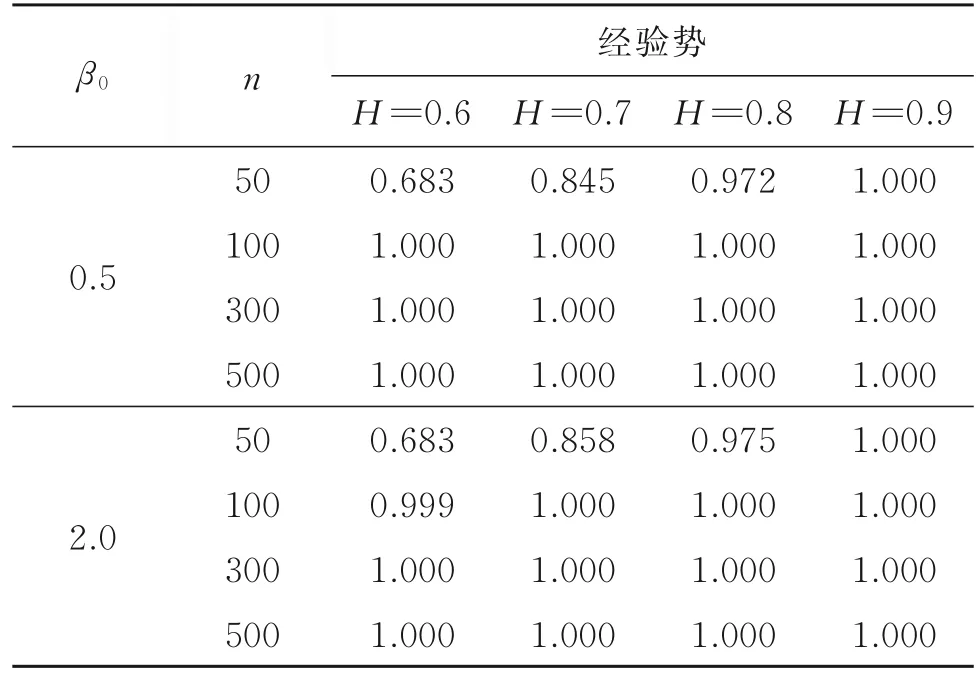
表6 情況3統計量Wn的經驗勢Table 6 The empirical power of statistic Wnin case 3
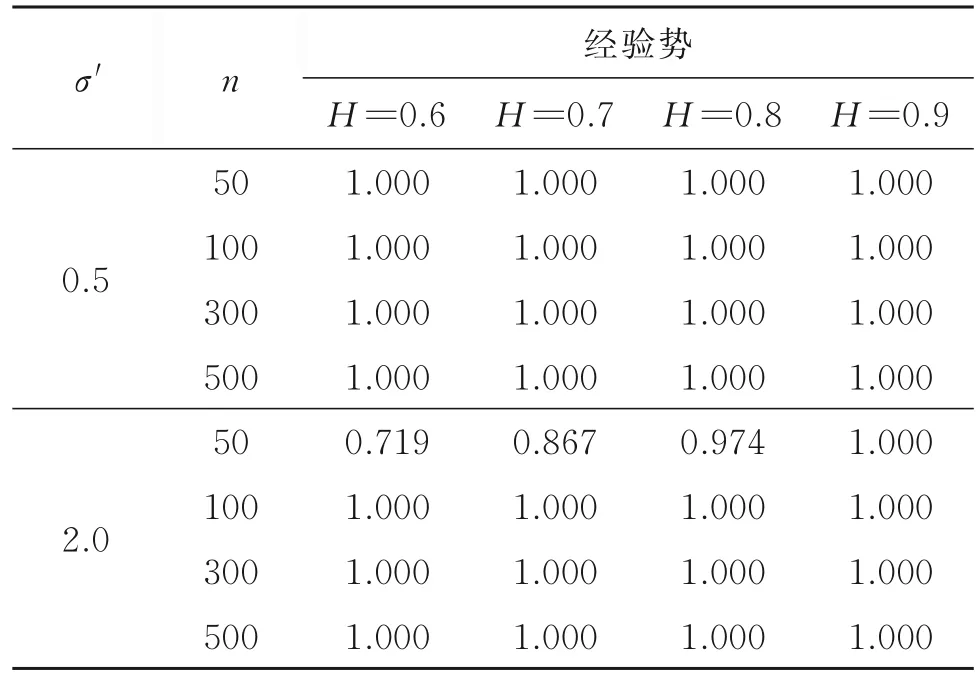
表7 情況4統計量Wn的經驗勢Table 7 The empirical power of statistic Wnin case 4
3 實例分析
將本文方法用于分析1854—1989年北半球經季節調整的月均氣溫,共1632個觀測值,結果如圖1所示。
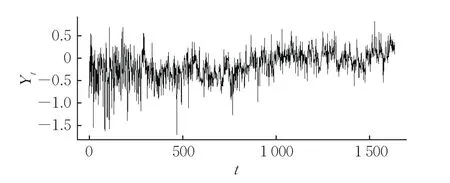
圖1 1854—1989年北半球經季節調整的月均氣溫Fig.1 Seasonally adjusted monthly deviations of the northern hemisphere temperature from 1854 to 1989
首先,對原始序列Yt使用局部whittle估計法,得到其Hurst指數的估計值=0.6939,接近于0.7,此時在α=0.05處的臨界值約為0.247。然后,對原始數據Yt做一階差分得到序列Xt,基于序列Xt計算得到的檢驗統計量為0.0374,小于臨界值0.247,因此認為該組數據中不存在趨勢項變點。
此前已有不少研究對該數據集進行了分析,并得到不同結論,如DEO等[23]認為數據存在趨勢項變點,WANG[24]則認為沒有足夠的證據證明序列中存在趨勢項變點,SHAO[25]通過檢驗認為序列存在均值變點。
4 結 論
關于趨勢項變點的檢驗問題,在獨立或短記憶模型假設下的研究較多,而在長記憶模型下的研究較少。本文研究了分數布朗運動趨勢項變點的檢驗問題,提出了一種Wilcoxon秩檢驗方法,基于觀測數據的一階差分序列構造了Wilcoxon秩統計量。在原假設下推導了檢驗統計量的極限分布。數值模擬結果驗證了本文方法在有限樣本下的有效性,且在樣本量足夠大的情況下對截距項變點和方差變點穩健。

