液體火箭發(fā)動機自適應(yīng)克里金可靠性分析*

胡偉飛 鄢繼銓 施欽楊 方健豪 劉振宇 譚建榮

1. 浙江大學(xué) 流體動力與機電系統(tǒng)國家重點實驗室，杭州 310027；2. 浙江大學(xué) 機械工程學(xué)院，杭州 310027

0 引言

近年來，隨著載人航天、探月工程等重大科技專項的實施，我國運載火箭進入了高強度發(fā)射期，對運載火箭高可靠、高質(zhì)量等方面提出了更高的要求。液體火箭發(fā)動機是運載火箭等航天飛行器的心臟，需要具備更高的可靠度，因此對其運行過程進行故障監(jiān)測，從而在一定程度上提高運載火箭的可靠性。液體火箭發(fā)動機是一類高度復(fù)雜的動力系統(tǒng)，由大量、相互之間存在廣泛聯(lián)系同時又進行著不同工作過程的組件和部件構(gòu)成。隨著運載火箭的有效載荷不斷增加，且外界工作環(huán)境存在不確定性，使發(fā)動機工作在較為復(fù)雜的惡劣環(huán)境中。因此對其可靠性提出了更高的要求，液體火箭發(fā)動機可靠性研究受到廣泛重視[1-3]。

傳統(tǒng)可靠性分析的方法有：近似解析法、數(shù)值模擬法以及代理模型法，均適用于液體火箭發(fā)動機可靠性分析。近似解析法主要指的是一階可靠度法(FORM)[4]、二階可靠度法(SORM)[5]，其通過將設(shè)計點的失效域邊界線性化得到失效概率的估計。該類方法的缺點有：需要顯性液體火箭發(fā)動機數(shù)學(xué)模型，而且在非線性問題上應(yīng)用效果較差。數(shù)值模擬法主要指蒙特卡羅模擬法[6]，該方法采用一定數(shù)量的樣本并獲取對應(yīng)的響應(yīng)值，基于這些樣本計算失效概率。計算結(jié)果的精度隨采樣的樣本點增加而提高。現(xiàn)有方法所需的計算成本和時間成本非常龐大。尤其針對液體火箭發(fā)動機這樣的關(guān)鍵裝備，獲取失效樣本的成本過高，收集大量數(shù)據(jù)不切實際。

基于上述結(jié)論，有學(xué)者提出了代理模型法，其主要原理為采用代理模型代替真實物理模型，運用蒙特卡羅模擬計算失效概率。蒙特卡洛法需要較為龐大的樣本量，針對此，代理模型法提出將對應(yīng)樣本點輸入代理模型當(dāng)中，以較少的樣本數(shù)量進行實時預(yù)測輸出，減少真實物理模型或耗時的有限元仿真模型的運算次數(shù)與計算時間。現(xiàn)有的代理模型主要包括：多項式響應(yīng)面模型[7]、神經(jīng)網(wǎng)絡(luò)模型[8]、支持向量機[9]以及克里金模型[10]。本文采用的代理模型為克里金模型，其優(yōu)勢在于其可以進行全局代理，獲取了定義域內(nèi)樣本點區(qū)間的預(yù)測值，還包含預(yù)測局部方差，用于表征局部不確定性。

克里金模型對于模型的預(yù)測精確程度將直接影響分析結(jié)果的準確性，因此基于較少的樣本構(gòu)建精確的克里金模型是當(dāng)前該領(lǐng)域的主要研究方向。Echard等[11]首先提出重要性采樣的思想，引入重要性密度分布函數(shù)提高采樣效率。在此基礎(chǔ)上，Xiao等[12]提出了分層重要性采樣的方法，進一步提高采樣效率。此外Zhang等[13]提出的自適應(yīng)克里金面向重要度采樣方法和Wang等[14]提出的基于錯誤率的自適應(yīng)克里金可靠性分析方法，為有效提高采樣效率，擬合精確的失效邊界提供新思路。但通過分析發(fā)現(xiàn)，現(xiàn)有方法大多存在樣本點聚集現(xiàn)象， 即同一區(qū)域內(nèi)樣本點數(shù)量過于密集，這將導(dǎo)致計算資源的浪費。同時，現(xiàn)有方法的收斂條件不精準，容易導(dǎo)致過采樣。

本文采用代理模型對液體火箭發(fā)動機進行可靠性分析。針對現(xiàn)有克里金代理模型存在的兩個弊端，提出了基于泰森多邊形區(qū)域劃分自適應(yīng)克里金的液體火箭發(fā)動機可靠性分析方法。該方法能夠高效的構(gòu)建克里金代理模型，并用于預(yù)測液體火箭發(fā)動機的失效概率。

1 基于代理模型的液體火箭發(fā)動機可靠性分析

1.1 液體火箭發(fā)動機可靠性分析現(xiàn)狀

液體火箭發(fā)動機自身結(jié)構(gòu)極為復(fù)雜，不同組件之間的相互作用也會對運行過程產(chǎn)生影響，存在隨機性。圖1給出了F-1發(fā)動機的組成圖。針對液體火箭發(fā)動機的可靠性分析，王婷婷等[1]提出威布爾分布和Bayes估計分析方法，研究液體火箭發(fā)動機壽命分布參數(shù)以及該方法的可靠度。但這種方法未考慮液體火箭發(fā)動機實際運行時復(fù)雜環(huán)境給可靠性分析帶來的不確定性，無法得到實時的可靠性分析結(jié)果。

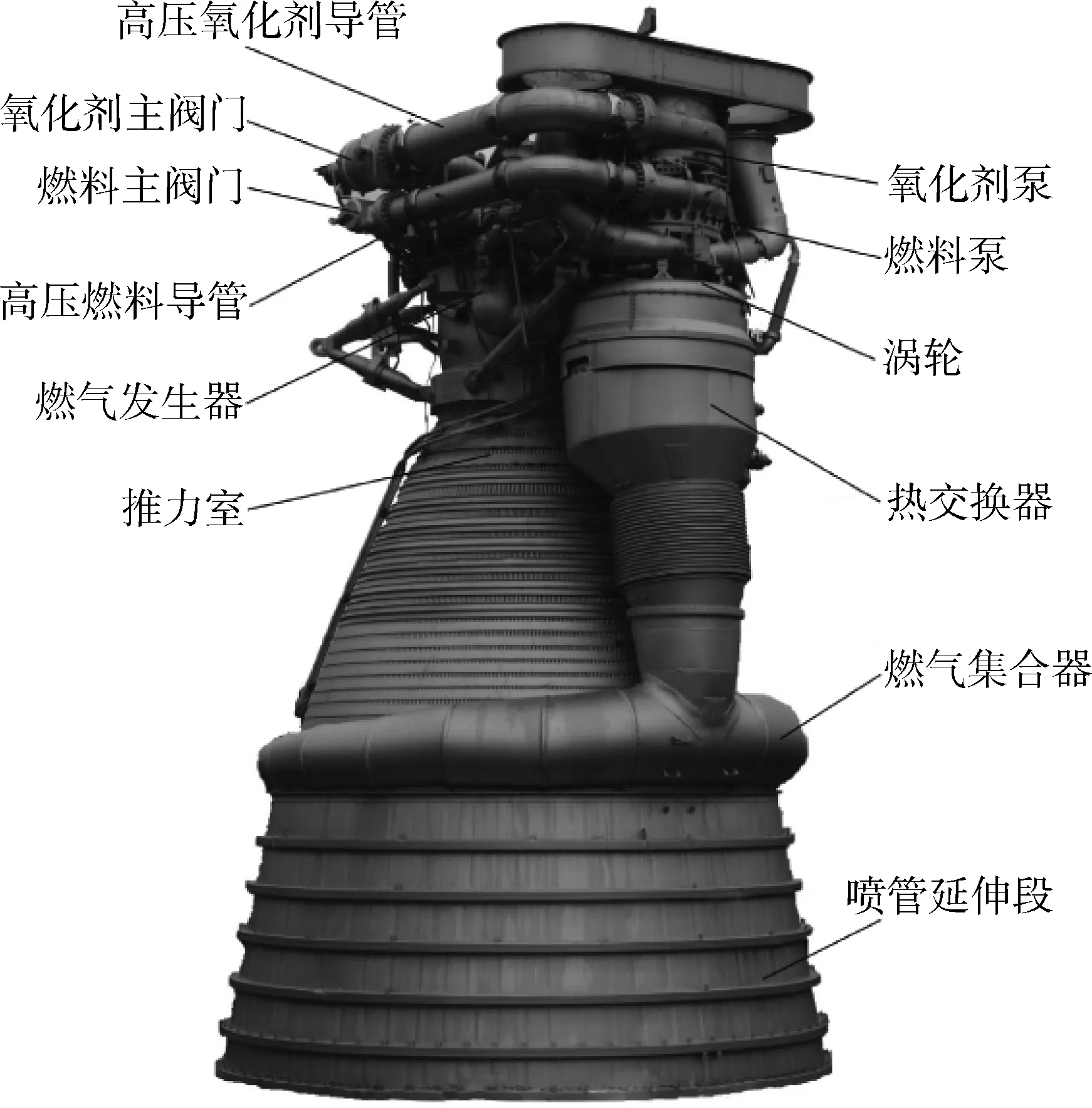
圖1 F-1液體火箭發(fā)動機組成圖[15]

1.2 基于代理模型的可靠性分析

本文提出采用克里金模型法對液體火箭發(fā)動機進行可靠性分析。通過建立精確的液體火箭發(fā)動機克里金模型，預(yù)測液體火箭發(fā)動機的失效概率，采用的是傳統(tǒng)蒙特卡羅模擬方法。該方法通過采樣足夠數(shù)量的樣本，統(tǒng)計處于失效域的樣本數(shù)量，依照式(1)[16]計算出系統(tǒng)的失效概率PF。

(1)

式中，NG(x)<0定義為失效樣本數(shù)量；G代表構(gòu)建的克里金代理模型；NMCS為采用蒙特卡洛法采樣樣本點總數(shù)量。

蒙特卡羅方法計算過程中所采用的樣本點越多，得到的結(jié)果越近似于真實值。在蒙特卡羅模擬計算中，得到的結(jié)果與樣本點數(shù)需要滿足如式(2)[16]所示的關(guān)系。

(2)

fcov(PF)為失效概率的差異系數(shù)，當(dāng)失效概率的差異系數(shù)值小于0.05時，可以認為得到結(jié)果較為可信。

2 基于泰森多邊形區(qū)域劃分的自適應(yīng)克里金模型構(gòu)建方法

依據(jù)前文獲得的液體火箭發(fā)動機在實際工作環(huán)境的失效概率，對其健康進行監(jiān)測。計算失效概率計算失放概率的前提是構(gòu)建精確的液體火箭發(fā)動機。針對傳統(tǒng)克里金代理模型構(gòu)建方法計算效率低，計算成本高等缺點，本文提出一種基于泰森多邊形區(qū)域劃分的自適應(yīng)克里金代理模型構(gòu)建方法，以較少的樣本構(gòu)建精確的克里金代理模型。

2.1 基于泰森多邊形的全局區(qū)域劃分

本文所提出的方法采用了全局區(qū)域劃分策略，根據(jù)泰森多邊形的區(qū)域分割方式，進行空間區(qū)域劃分。具體流程如下：

根據(jù)已有樣本點，生成所有相鄰兩個樣本點的垂直平分面，進而由生成的垂直平分面將空間劃分成不同的區(qū)域，此區(qū)域為泰森多邊形區(qū)域。圖2展示了一個由泰森多邊形劃分的二維案例。

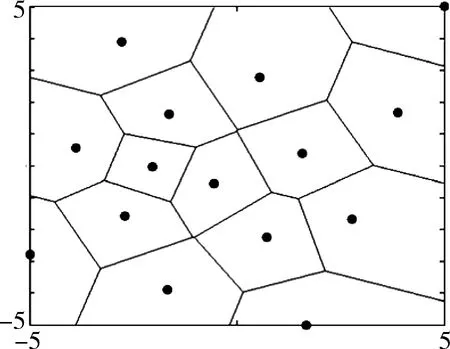
圖2 一個由泰森多邊形劃分的二維案例[17]

由于高維樣本點進行泰森多邊形分割后的多邊形單元是高維不規(guī)則邊界的多面體，因此很難對其進行數(shù)學(xué)描述。因此，本文采用蒙特卡羅方法生成大量隨機點從而近似描述高維問題中泰森多邊形區(qū)域。通過計算候選樣本點到空間中所有樣本點的距離，將每個候選樣本點劃分至已有的樣本點中最近的點。

2.2 改進留一法

在全局區(qū)域劃分之后，需要選擇出在失效邊界附近的區(qū)域。該區(qū)域稱為最敏感區(qū)域，采用改進留一法來實現(xiàn)。留一法[18](Leave-One-Out，簡稱LOO)是一種模型驗證優(yōu)化方法，常通過交叉驗證檢驗?zāi)Ｐ偷臏蚀_性。以下是留一法的具體流程：

假設(shè)空間中有N個樣本，每次剔除1個樣本，利用剩余的N-1個樣本重新構(gòu)建模型，并采用被剔除的樣本作為測試集計算模型誤差，進行N次流程循環(huán)，具體如式(3)所示。

(3)

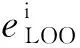
將上述流程循環(huán)N次，最終得到所有樣本點的預(yù)測誤差。定義預(yù)測誤差最大的樣本點所屬的泰森多邊形區(qū)域為最敏感區(qū)域。

以上是傳統(tǒng)留一法的過程。由于傳統(tǒng)留一法是將剩下的一個點作為測試集，通過比較在這個點的響應(yīng)值的偏差來比較泰森多邊形區(qū)域的好壞，整個流程計算時間較長，計算成本較高。對于可靠性分析而言，只需要在失效邊界附近構(gòu)建精確，能夠較好的擬合出極限狀態(tài)函數(shù)等于0(G(x)= 0)對應(yīng)的曲面即可。因此不必構(gòu)建一個全局精確的克里金模型，減少不必要的計算量和成本消耗。在失效邊界以外的區(qū)域，它的響應(yīng)值不一定精確，只需要符號正確即可。

基于以上推論，本文所提出的方法對留一法進行修改，使其更適用于可靠性分析領(lǐng)域，具體流程如下：

假設(shè)空間中有N個樣本，每次剔除1個樣本，利用剩余的N-1個樣本構(gòu)建克里金模型Gi。根據(jù)構(gòu)建的克里金模型Gi計算剔除后的失效概率Pfi，共循環(huán)N次。除此之外采用N個樣本構(gòu)建一個克里金模型，計算實際失效概率Pf。按照如式(3)，計算針對每個模型的失效概率偏差，最后將偏差最大模型對應(yīng)的泰森多邊形區(qū)域選為最敏感區(qū)域。

2.3 主動學(xué)習(xí)函數(shù)

在計算得到最敏感泰森多邊形區(qū)域之后，需在這個最敏感區(qū)域當(dāng)中選取下一個樣本點添加進訓(xùn)練集，重新構(gòu)建克里金模型。本文采用的選擇樣本點方法為主動學(xué)習(xí)函數(shù)。主動學(xué)習(xí)函數(shù)用于確定構(gòu)建模型的下一個最佳采樣點，對于自適應(yīng)克里金模型應(yīng)用于可靠性分析領(lǐng)域必不可少。本文所采用的主動學(xué)習(xí)函數(shù)是預(yù)期可行性函數(shù)(Expected Feasibility Function，EFF)。

預(yù)期可行性函數(shù)fEF是由預(yù)期改進函數(shù)(Expected Improvement Function，EIF)改進而來的，由Jones等[19]在高效全局優(yōu)化方法中首次提出。該預(yù)期改進函數(shù)是用來選擇一個新訓(xùn)練樣本點的位置。但是預(yù)期改進函數(shù)更多應(yīng)用于構(gòu)建全局精確的模型。因此本文引入了預(yù)期可行性函數(shù)，以表示預(yù)期響應(yīng)的真實值滿足等式約束G(x)=a的程度。其具體計算如式(4)[20]所示。

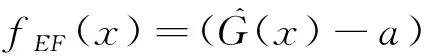
(4)

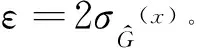
從敏感區(qū)域樣本點中選取預(yù)期可行性函數(shù)值最大的點作為下一個訓(xùn)練樣本點。通過添加新的訓(xùn)練樣本點，建立新的克里金代理模型，采用該模型計算另一組預(yù)期可行性函，進而由該預(yù)期可行性函數(shù)選擇另一個新的訓(xùn)練點。以此類推，直到最大點的預(yù)期可行性函數(shù)值低于指定的公差。

失效概率估計的準確性總是隨著預(yù)期可行性函數(shù)停止準則的閾值的降低而增加的，但是代價是所需樣本點更多，增加了計算成本。本文采用最大的預(yù)期可行性函數(shù)值小于0.001作為迭代更新的收斂判據(jù)。

2.4 整體流程

基于前文提及的方法，本文提出了一種基于泰森多邊形區(qū)域劃分自適應(yīng)克里金的液體火箭發(fā)動機可靠性分析方法。該方法主要含有3個過程，包括全局泰森多邊形區(qū)域劃分，最敏感區(qū)域選擇和最有價值樣本點選擇。其具體流程如圖3所示。

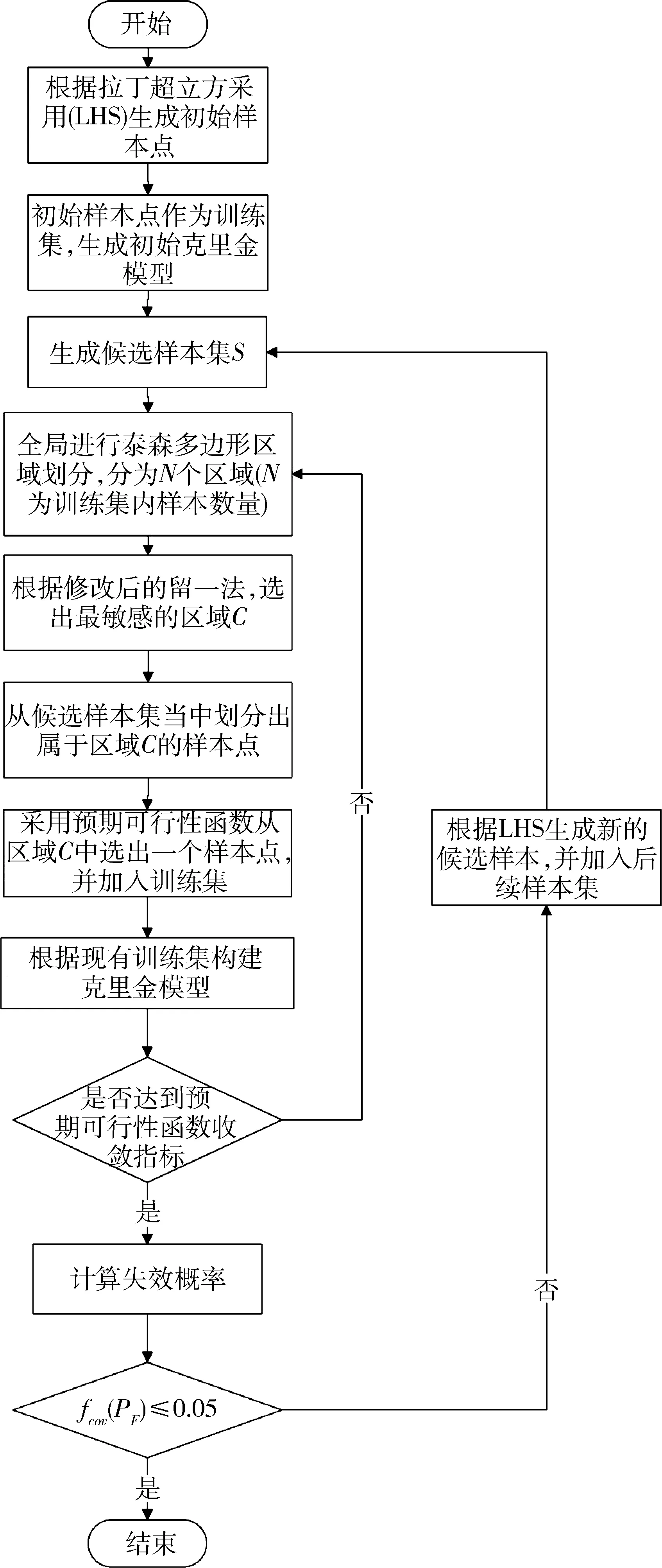
圖3 基于泰森多邊形區(qū)域劃分自適應(yīng)克里金的液體火箭發(fā)動機可靠性分析方法流程圖

步驟1：根據(jù)不同輸入變量分布生成少量的初始樣本點X0，其中是采用拉丁超立方采樣(Latin Hypercube Sampling，LHS)方法生成初始樣本點；

步驟2：將初始樣本點X0及其對應(yīng)的輸出值作為訓(xùn)練集X，生成初始液體火箭發(fā)動機克里金模型。具體包括：根據(jù)訓(xùn)練集樣本X，輸入到實際系統(tǒng)或有限元仿真模型中獲得其對應(yīng)的輸出Y；然后根據(jù)案例類型，設(shè)置克里金模型核函數(shù)類型，設(shè)置初始參數(shù)，設(shè)置參數(shù)優(yōu)化范圍；將訓(xùn)練集輸入，采用MATLAB的DACE工具箱構(gòu)建克里金模型；

步驟3：根據(jù)不同輸入變量分布生成一定數(shù)量候選樣本集S，生成候選樣本點使用的是拉丁超立方采樣方法；

步驟4：在全局內(nèi)進行區(qū)域劃分，分為N個區(qū)域(N為現(xiàn)有訓(xùn)練集內(nèi)樣本數(shù)量)。全局區(qū)域劃分時采用泰森多邊形劃分策略，使得每個多邊形空間內(nèi)僅包含一個樣本點，且多邊形內(nèi)的任意位置離該多邊形的樣本點距離最近；

步驟5：根據(jù)改進留一法，計算失效概率偏差，選出最敏感的區(qū)域C；

步驟6：從候選樣本集當(dāng)中劃分出屬于區(qū)域C內(nèi)的樣本點；

步驟7：采用主動學(xué)習(xí)函數(shù)從區(qū)域C中選出一個樣本點，并加入訓(xùn)練集X，主動學(xué)習(xí)函數(shù)采用的是預(yù)期可行性函數(shù)；

步驟8：根據(jù)現(xiàn)有訓(xùn)練集重新生成液體火箭發(fā)動機克里金模型，具體細節(jié)如步驟2；

步驟9：判斷是否達到主動學(xué)習(xí)函數(shù)收斂指標，若未滿足則重復(fù)步驟4至步驟8。收斂指標指的是式(5)，當(dāng)最敏感區(qū)域內(nèi)所有樣本點都滿足條件時認為收斂。

max(fEF(x))≤0.001

(5)

步驟10：計算當(dāng)前克里金模型下的失效概率，計算方法采用的是蒙特卡羅模擬法；

步驟11：根據(jù)式(2)判斷是否滿足蒙特卡羅法收斂指標失效概率協(xié)方差是否小于0.05，若未滿足，則根據(jù)生成新的候選樣本加入候選樣本集S，并返回步驟3；

步驟12：基于現(xiàn)有液體火箭發(fā)動機克里金模型，根據(jù)蒙特卡羅模擬法計算系統(tǒng)失效概率Pf。

3 案例分析

本章采用的測試案例是基于楊晉朝[21]提供的液體火箭發(fā)動機失效數(shù)據(jù)，得到的液體火箭發(fā)動機性能方程，如式(6)所示：

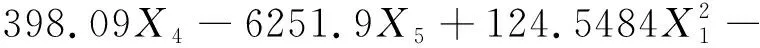
(6)

式中，5個輸入變量分別是氧泵入口壓力X1、氧泵后溫度X2、氫泵入口壓力X3、氫泵后溫度X4以及燃氣發(fā)生器室壓X5均服從正態(tài)分布，均值0.5，方差0.1，5個變量相互獨立。

在測試過程中，初始樣本點選擇為12個，每次生成的候選樣本集數(shù)量為105個。將本文所提出的方法與傳統(tǒng)的自適應(yīng)克里金模型-蒙特卡羅模擬方法[20](An active learning reliability method combining Kriging and Monte Carlo Simulation, AK-MCS)作比較，并采用蒙特卡羅模擬結(jié)果作為真實值。并通過5次仿真測試后求取平均結(jié)果，驗證本方法的魯棒性。最終的實驗對比結(jié)果如表1所示。表中展示了兩種方法所需的樣本點個數(shù)和誤差率。從表中可以看出，本文所提出方法與傳統(tǒng)自適應(yīng)采樣方法的計算誤差都小于1%，達到精度計算要求。此外，本文提出方法所需的樣本點個數(shù)僅為163.4個，而AK-MCS方法需要314.2個樣本點。在本案例中，本文所提出方法效率比AK-MCS方法提高了48%，相對于傳統(tǒng)方法能夠快速、準確地對液體火箭發(fā)動機進行可靠性分析。

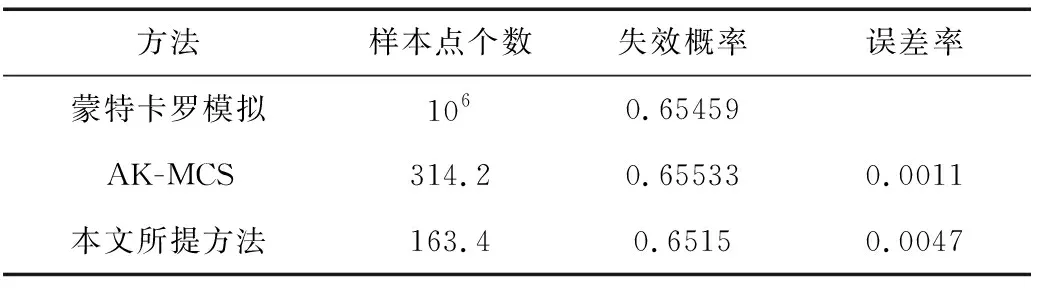
表1 測試案例結(jié)果對比

4 結(jié)論

針對傳統(tǒng)可靠性分析方法計算效率低的問題，本文提出了一種基于泰森多邊形區(qū)域劃分自適應(yīng)克里金的液體火箭發(fā)動機可靠性分析方法。利用泰森多邊形進行全局區(qū)域劃分，結(jié)合改進留一法對區(qū)域進行篩選，極大程度的提高了模型構(gòu)建的效率，能夠用較少的樣本點構(gòu)建同樣精度要求的液體火箭發(fā)動機模型。同時，該模型能夠結(jié)合外界載荷的不確定性，對發(fā)動機進行健康監(jiān)測和故障檢測。在理論測試中，基于本文提出方法構(gòu)建的代理模型測試計算誤差與其他模型相比小于1%，效率提高了48%。本文側(cè)重于理論方法研究，如有真實液體火箭發(fā)動機模型或有限元仿真模型，采用本方法也能對其進行可靠性分析，計算出特定工作狀況下的失效概率。

后續(xù)工作可以從液體火箭發(fā)動機時變可靠性分析研究著手，將外界載荷的時變特性納入考量，研究一種高效的時變可靠性分析方法。