橫觀各向同性土中大直徑樁的縱向振動分析

楊冬英, 馮瑋杰, 李學東

(1.蘇州科技大學土木工程學院， 蘇州 215011； 2.江蘇蘇州地質工程勘察院， 蘇州 215011)

近年來樁土相互作用的動力問題作為巖土工程和地震工程的熱點問題被學者們廣泛研究，其研究成果也被廣泛運用到工程實際中。其中，針對工程實踐中大量應用的大直徑樁，其振動機理研究也在持續中。目前，傳統的一維桿件理論已不再適用，Love在Rayleigh考慮桿件的橫向慣性效應基礎上得到了修正后的桿件運動方程[1]，此方程被運用到大直徑樁的研究上。龔志超等[2]、Li等[3]、Liang等[4]、何偉杰等[5]、何夢澤等6]基于Rayleigh-Love桿模型分別對均質、非均質土中大直徑樁的縱向振動規律進行了研究。李強等[7]、呂述暉等[8]、李曼等[9]考慮土體的三維波動效應，給出了大直徑樁縱向振動的理論解。

以上對于大直徑樁的動力特性研究都是將樁周土視為各向同性介質。然而，在實際工程中，土顆粒在沉積的過程中其橫向及縱向性質往往產生差異，橫觀各向同性更加符合這種規律[10]。郭楠等[11]利用試驗對橫觀各向同性土與各向同性土進行對比分析得到了二者力學特性不盡相同的結論。因此，研究橫觀各向同性土中樁的振動規律更加具有實際意義。目前，學者們在此方面已經取得了一些成果。Chen等[12]忽略土體應力沿深度變化，求解了橫觀各向同性土中彈性樁的扭轉振動響應解。張智卿等[13]、鄭長杰等[14]考慮土體應力沿深度變化分別對實心樁、管樁在橫觀各向同性土中的扭轉振動規律進行了研究。高洪波[15]在樁底固定邊界的條件下研究了單樁在飽和橫觀各向同性土縱向振動的動力響應解。吳文兵[16]基于虛土樁法給出了單樁在橫觀各向同性土中的縱向振動響應解。但是，到目前為止，將橫觀各向同性土與大直徑樁結合進行的振動規律研究還相對不足。考慮到大直徑樁在工程實際中的廣泛使用以及土體的實際情況，研究大直徑樁在橫觀各向同性土中的振動規律就顯得十分必要。

現視土體為橫觀各向同性土，考慮橫向慣性力，進行大直徑樁的縱向振動特性研究，并對理論研究解析解的準確性展開對比分析。

1 計算模型與基本假定

橫觀各向同性土-大直徑樁的計算模型為三維軸對稱模型如圖1所示。z為縱向坐標軸，r為徑向坐標軸。其中，土體密度為ρ，土體底部為黏彈性支承，并簡化為Kelvin線性分布式，其分布式彈性系數和阻尼系數分別為ks、cs。樁長為H，樁徑為r0，密度為ρp，彈性模量為Ep，樁頂受到F0eiωt的簡諧激振力，樁側壁受到來自土體的摩擦力，表示為fs，樁底采用黏彈性支承，彈性系數和阻尼系數分別用kb、cb表示。

z為縱向坐標軸；r為徑向坐標軸；H為樁長；r0為樁徑；ks、cs分別為分布式彈性系數和阻尼系數；fs為樁側壁受到來自土體的摩擦力；kb、cb分別為彈性系數和阻尼系數；F(t)=F0eiωt為樁頂受到的簡諧激振力圖1 樁-土動力系統力學模型Fig.1 Mechanical model of pile-soil dynamic system

基本假定如下。

(1)樁周土為橫觀各向同性黏彈性土，土體材料阻尼采用黏性阻尼形式，其大小與應變率成正比。

(2)土體頂部為自由表面且正應力為0，底部為黏彈性支承。

(3)忽略土體徑向、切向位移，只考慮土體縱向位移。

(4)樁身為均質黏彈性材料，樁底為黏彈性支承。

(5)樁土變形為小變形且樁土接觸面上應力、位移連續。

2 橫觀各向同性土體運動方程

2.1 方程的建立

在三維軸對稱條件下，根據丁皓江[17]對橫觀各向同性材料本構方程的描述，忽略土體徑向、切向位移，建立土體運動方程為

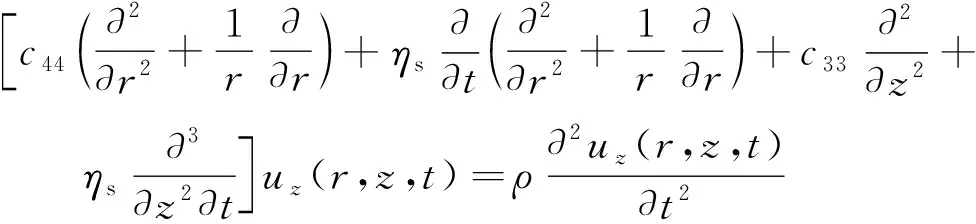
(1)

式(1)中：uz(r,z,t)=Uz(r,z)eiωt為土體縱向位移，Uz(r,z)為土體縱向位移幅值；ω為振動圓頻率；

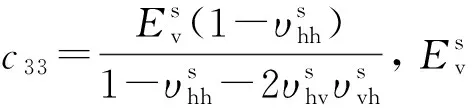
分別為各方向泊松比；ηs為土體黏性阻尼系數。

對式(1)進行整理，考慮土體諧和振動，將uz(r,z,t)=Uz(r,z)eiωt代入式(1)得

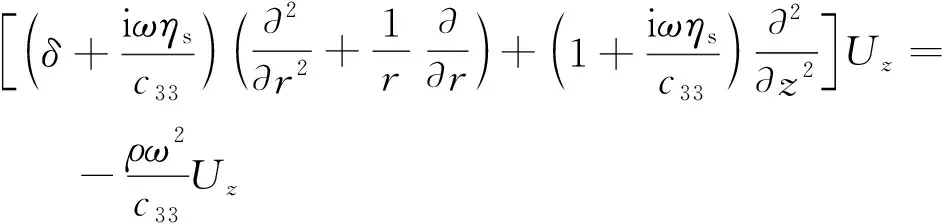
(2)

2.2 邊界條件

土體上部自由表面正應力為0，即

σz|z=0=0

(3)

土體底部為黏彈性支撐，即

(4)

無窮遠處土體位移趨于0，即

uz|r→∞=0

(5)

2.3 方程的求解

采用分離變量法，令Uz=R(r)Z(z)，代入式(2)，得

(7)

解方程組式(6)、式(7)，得

Z(z)=Csin(hz)+Dcos(hz)

(8)

R(r)=AK0(qr)+BI0(qr)

(9)

式(9)中：I0(qr)、K0(qr)分別為第一類、第二類零階修正貝塞爾函數；A、B、C、D均為待定常數。

根據邊界條件[式(5)]，得B=0；根據邊界條件[式(3)]，得C=0；根據邊界條件[式(4)]，得

(10)

由式(8)～式(10)可得土體縱向位移解為

(11)

樁周土對樁側壁的縱向剪應力幅值可表示為

(12)

為了計算方便，引入下列無量綱：

3 大直徑樁的縱向振動方程

3.1 方程的建立

根據Rayleigh-Love桿理論，建立黏彈性大直徑樁的縱向振動方程為

(13)

式(13)中：wp(z,t)=Wp(z)eiωt為樁的縱向位移，Wp(z)為樁縱向位移幅值；Ap、ηp、υp分別為樁身截面積、阻尼系數、泊松比；fs=2πr0τrzeiωt為樁側摩阻力。

對式(13)進行整理，考慮樁身諧和振動，將wp(z,t)=Wp(z)eiωt代入式(13)得

(14)

3.2 邊界條件

樁頂受到外力作用為

=-F(t)

(15)

樁底為黏彈性支撐，即

(16)

樁土接觸面處位移連續，即

uz|r=r0=wp

(17)

3.3 方程的求解

解方程[式(14)]，得

(18)

式(18)中：

(19)

將式(11)、式(18)代入連續條件[式(17)]，得

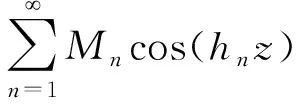
(20)

利用三角函數系的正交性，式(20)兩邊同時乘以cos(hnz)，得

(21)

式(21)中：

為方便計算，引入以下無量綱變量：

則

根據式(18)、式(19)、式(21)，得

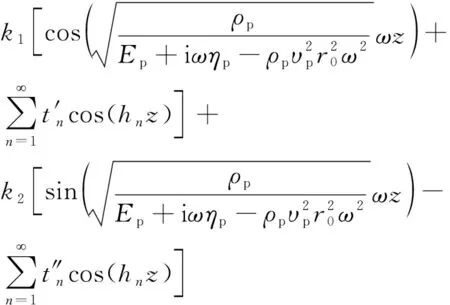
(22)

式(22)中：

將式(22)代入邊界條件[式(15)]、[式(16)]得

(23)

(24)

式(24)中：

因此，樁頂復剛度及無量綱化可表示為

(25)

(26)

樁頂速度導納無量綱可以表示為

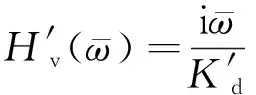
(27)

V(t)=IFT[Hv(ω)q(ω)]

(28)

式(28)中：IFT表示Fourier逆變換。對式(28)無量綱化可以得到速度時域響應無量綱表達式為

(29)

4 參數分析

4.1 土體動力響應分析

根據式(11)、式(12)、式(21)可以得到樁土接觸面處土體剪切復剛度為

(30)

KK=2πc33KK′

(31)

式中：

定義剪切復剛度無量綱化實部為KK′r，表示土層剛度即抵抗變形的能力；虛部為KK′i，表示土層阻尼即反映能量的耗散。從式(30)可以看出，土體剪切復剛度大小一方面由土體自身參數決定，如橫觀各向同性參數δ，另一方面取決于樁身參數，如樁徑r0，這也體現了樁土振動過程中的耦合作用。

圖2 不同橫觀各向同性參數情況下土體剪切復剛度隨頻率、深度變化圖Fig.2 Variation diagram of complex shear stiffness of soil with frequency and depth under different transversely isotropic parameters

圖3 不同橫觀各向同性參數情況下土體剪切復剛度隨深度變化圖Fig.3 Variation diagram of complex shear stiffness of soil with depth under different transversely isotropic parameters

圖5給出了不同樁徑r0情況下土體剪切復剛度隨頻率、深度變化三維圖。從圖5(a)、圖5(b)中可以看出，樁頂處土體剪切復剛度實部和虛部幅值均隨著頻率增大而增大，而隨著深度的變化，頻率影響同樣變小。

從圖6可以看出，土體剪切復剛度實部受到r0變化的影響僅發生在土體頂部和底部，而在土體中部區域，r0變化產生的影響可忽略不計，虛部阻尼隨著r0增大而增大，但增大幅度較小。

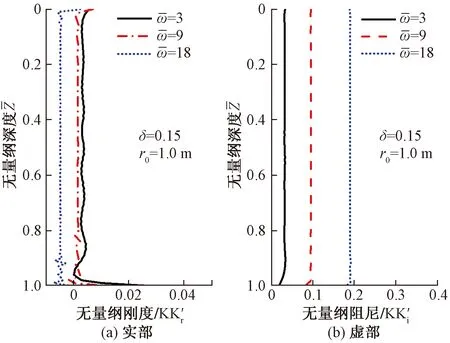
圖4 不同頻率情況下土體剪切復剛度隨深度變化圖Fig.4 Variation diagram of complex shear stiffness of soil with depth under different frequencies

圖5 不同樁徑情況下土體剪切復剛度隨頻率、深度變化圖Fig.5 Variation diagram of complex shear stiffness of soil with frequency and depth under different pile diameters

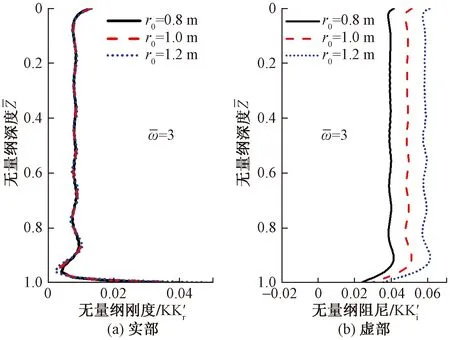
圖6 不同樁徑情況下土體剪切復剛度隨深度變化圖Fig.6 Variation diagram of complex shear stiffness of soil with depth under different frequencies

由此可以看出，土體剪切復剛度大小主要由土體自身參數和外部荷載頻率決定，樁身參數對剛度影響較小，但對于阻尼影響不可忽略。

4.2 樁頂動力響應分析

4.2.1 土體橫觀各向同性參數變化的影響

圖7 橫觀各向同性參數對樁頂速度幅頻和時域曲線的影響Fig.7 Influence of transversely isotropic parameters on pile top velocity amplitude frequency and time domain curve

4.2.2 樁徑變化及橫向慣性效應的影響

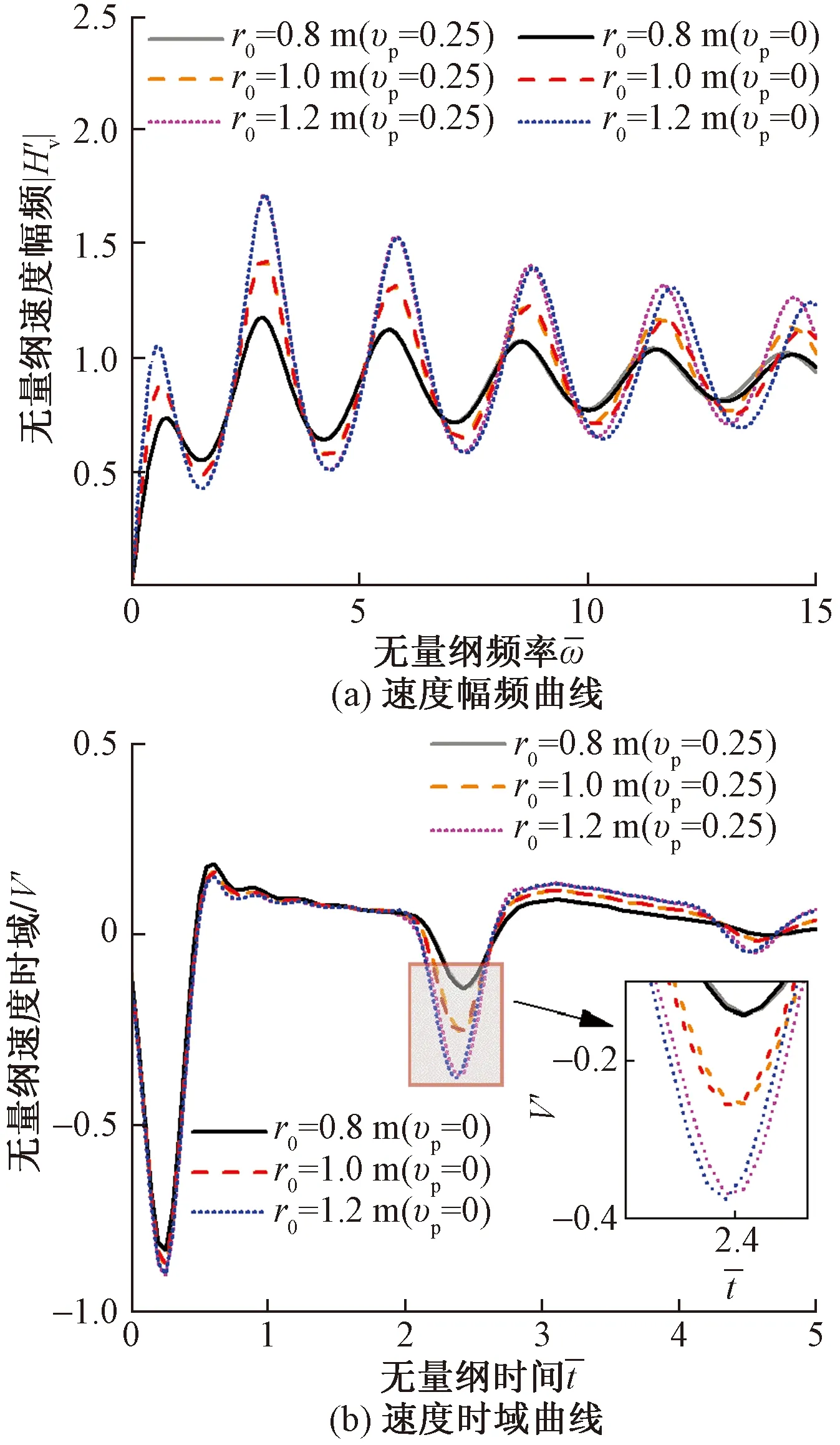
圖8 樁徑變化及橫向慣性效應對樁頂速度幅頻和時域曲線的影響Fig.8 Influence of pile diameter variation and lateral inertia effect on pile top velocity amplitude frequency and time domain curve

圖8給出了不同樁徑r0及有無考慮橫向慣性力情況下樁頂速度幅頻和時域曲線。從圖8(a)可以看出，隨著r0的增大，樁頂速度幅頻共振峰值大幅增大，考慮橫向慣性效應(υp=0.25)時，共振頻率在高頻段減小，在低頻段基本不變。從圖8(b)可以看出，隨著r0的增大，反射信號強度增大且考慮橫向慣性力時反射信號位置向右偏移。另外，可以發現，樁徑越大，橫向慣性力的影響越明顯。這表明，橫向慣性效應是影響大直徑樁振動的一個重要因素。

4.2.3 土體黏性阻尼系數變化的影響

圖9給出了土體黏性阻尼系數ηs變化對樁頂速度幅頻和時域曲線的影響。相比于滯回阻尼對振動較小的影響，考慮的土體黏性阻尼對樁的振動影響很大且更加符合實際情況。從圖9(a)中可以看出，隨著ηs的增大，樁頂速度幅頻共振峰值呈現明顯衰減趨勢，且共振峰明顯變寬。可以看到，當ηs=5×105N·s/m2時，樁頂速度幅頻曲線在高頻段衰減成一條直線。從圖9(b)可以看出，ηs的增大也使得反射信號強度大幅度減小，且在ηs=5×105N·s/m2時反射信號很弱，另外，反射信號寬度也明顯變寬。

圖9 土體黏性阻尼系數對樁頂速度幅頻和時域曲線的影響Fig.9 Influence of soil viscous damping coefficient on pile top velocity amplitude frequency and time domain curve

5 解的驗證

5.1 理論解退化

根據王敏中[18]對橫觀各向同性材料的研究，當彈性常數c44=G，c33=λ+2G(λ、G為第一、第二拉梅常數)時即可退化為各向同性材料。現與胡昌斌等[19]解對比分析，取土體泊松比υ=0.4，即當橫觀各向同性參數δ=0.167時退化為各向同性材料，再令υp=0即不考慮橫向慣性力可退化為胡昌斌解，其余參數取值與胡昌斌解中一致，具體如下：

圖10給出了退化為各向同性土時不同波速比條件下樁頂速度幅頻和時域曲線與胡昌斌解的對比，發現結果吻合較好，驗證了本文理論解的正確性。

5.2 有限元數值模擬

現對圓形截面樁和橫觀各向同性土相互振動進行有限元數值模擬，采用的單元類型為SOLID185實體單元，考慮到理論解中的軸對稱條件，建模采用1/4樁土模型，樁長20 m，樁徑1 m，樁側土半徑取24 m，高度取為樁長，樁、土底部黏彈性支承建模采用COMBIN14單元模擬，建模如圖11所示。樁身參數取值如表1所示， 橫觀各向同性土參數如表2所示，將樁土參數分配到對應的模型中。

網格劃分采用ANSYS軟件中的MESHTOOL工具，由于樁模型為主要研究對象且尺寸相對較小，網格劃分時采用邊長為0.5 m的網格，樁側土尺寸較大，網格劃分時采用邊長為2 m的網格，所有網格劃分方式均為自由劃分，在樁土接觸面處土體網格加密，保證了計算的精度，劃分結果如圖12所示。樁土1/4截面處施加對稱約束，土體外邊界和黏彈性支承底部施加固定約束，樁土接觸面處使用GLUE命令黏接，樁頂處施加半正弦脈沖荷載，求解完成后可以在后處理中得到樁頂速度時域曲線。

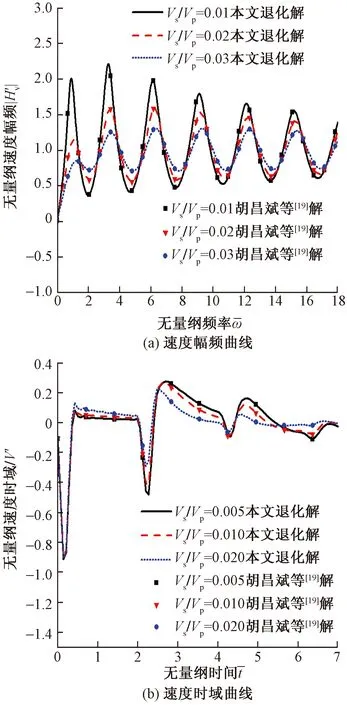
圖10 不同波速比情況下本文解與胡昌斌解對比Fig.10 Comparison between the solution of this paper and Hu Changbin’s solution under different wave velocity ratios

圖11 模型示意圖Fig.11 Schematic diagram of model

圖13所示為不同橫觀各向同性參數δ情況下理論計算解與有限元數值解的對比。可以看出，本文理論解吻合情況較好。另外，隨著δ的增大，反射信號峰值減小，這與理論解中δ變化的影響一致，相互驗證了本文理論解與數值解的正確性。

表1 樁參數取值Table 1 Values of pile parameters

圖12 網格劃分示意圖Fig.12 Schematic diagram of grid division

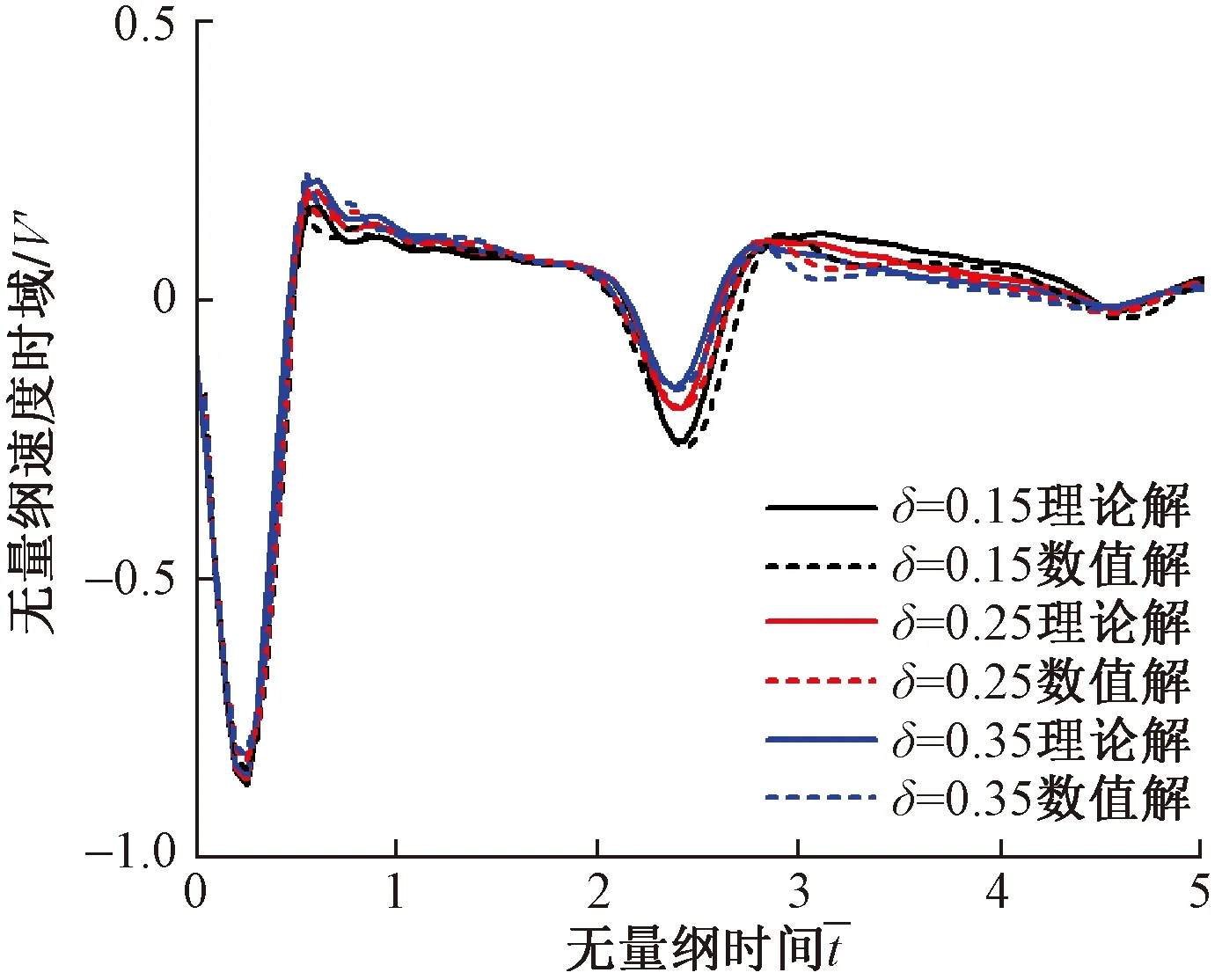
圖13 不同橫觀各向同性參數情況下理論解與數值解對比Fig.13 Comparison of theoretical and numerical solutions under different transversely isotropic parameters

表2 橫觀各向同性土參數取值Table 2 Parameters of transversely isotropic soil

6 結論

考慮土體顆粒沉積過程中各向性質的差異，視土體為橫觀各向同性黏彈性材料，研究大直徑樁在其中的縱向振動規律，得到以下幾點結論。

(1)橫觀各向同性參數的增大導致土體剪切復剛度增大進而對樁頂速度幅頻和時域曲線影響顯著。具體表現為隨著橫觀各向同性參數的增大，共振峰值減小，反射信號強度降低。

(2)樁徑變化對土體剪切復剛度影響較小，但對樁頂動力響應有明顯影響，具體表現為樁徑增大會顯著增大樁頂速度幅頻曲線的共振峰值和時域曲線的反射信號強度，并且樁徑越大，橫向慣性效應的影響越明顯。

(3)土體黏性阻尼系數的變化對樁的縱向振動影響明顯，具體表現為阻尼系數增大會減小樁頂速度幅頻曲線的共振峰值和共振頻率，也會降低速度時域曲線反射信號的強度，使反射信號峰值變寬。

(4)各向同性土中不考慮樁的橫向慣性力時，本文解能退化為胡昌斌解；本文解與數值計算的對比發現，兩種計算結果較吻合，驗證了本文理論解的正確性。