半球諧振陀螺諧波缺陷振動特性有限元分析

鄭 超,張 林,肖茵靜

（北京航天時代激光導航技術有限責任公司,北京 100094）

0 引言

半球諧振陀螺是利用半球殼振動敏感載體角度變化的慣性導航器件,它廣泛應用于航海、航空、航天等多個領域,具有高精度、高可靠性、長壽命的特點［1-3］。半球諧振子是半球諧振陀螺的核心敏感器件,其性能決定著陀螺儀的精度。諧振子是由具有高品質因數、低膨脹系數、極好化學穩定性的熔融石英材料精密加工而成,由于材料硬度高而脆,在制作加工過程中會因機床裝夾工裝與半球諧振子中心軸有偏差、加工刀具磨損或振動等造成諧振子質量分布不均勻。

目前,關于半球諧振陀螺諧波缺陷分布的研究,趙洪波［4］和明坤［5］研究了諧振子密度周向分布不均勻、阻尼周向分布不均勻與頻率裂解的影響;陳雪等［6］通過仿真實驗得到了如下結論:諧振子環向角薄壁厚度不均勻的四次諧波對陀螺輸出角速度影響較大,而一、二、三次諧波影響不大;趙小明等［7］分析了單點元的頻率裂解與四次諧波不平衡質量的線性對應關系;周闖等［8］通過動力學方程理論分析得到了特征頻率（即兩分歧的共振模態頻率）與特征向量（兩共振模態的方向）的顯式公式;Choi等［9］研究了多點質量半球殼的數學模型,得到了頻率裂解顯式表達式;Basaraba等［10］推導了半球陀螺沿子午方向的變厚度,得到了殼體厚度與質量的變化規律。然而,關于半球諧振陀螺諧波四類質量缺陷與頻率裂解的相關研究仍比較少。

本文為了更準確地對半球諧振陀螺進行調平,基于理想半球諧振子模型,針對不同諧波缺陷質量變化,研究了半球諧振子不同諧波質量缺陷的振型、固有頻率、頻率裂解等的變化規律。

1 半球諧振子諧波質量缺陷分布

根據Fourier函數進行展開,半球諧振子質量缺陷ρ可用Fourier函數ρ（φ）表示［11］,即

式（1）中,ρ1、ρ2、ρ3、ρ4、…分別為第1、2、3、4、…類缺陷的幅度大小,φ1、φ2、φ3、φ4、…分別為第1、2、3、4、…類缺陷的方位角位置。

半球諧振陀螺諧波質量缺陷分布有一次諧波缺陷、二次諧波缺陷、三次諧波缺陷和四次諧波缺陷等,如圖1所示,前四次諧波對陀螺的性能有影響。諧波缺陷導致半球諧振子出現雙本征軸（呈45°）,如圖2所示。諧振子沿其中每個軸的固有振動頻率可達到極大值和極小值,極大頻率與極小頻率的差值稱為頻率裂解Δf,即頻差,滿足式（2）

圖1 半球諧振子質量缺陷分布形式Fig.1 Distribution form of hemispherical harmonic oscillator mass defect

圖2 半球諧振子固有軸示意圖Fig.2 Schematic diagram of hemispherical harmonic oscillator natural axis

式（2）中,f1、f2分別為極小頻率和極大頻率。

諧波質量缺陷半球諧振子與理想半球諧振子的質量差值稱為相差質量值Δmi,即質量差,滿足式（3）

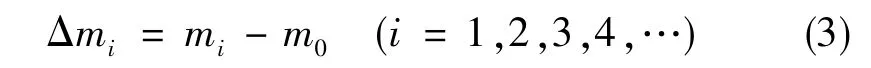
式（3）中,m0為理想半球諧振子質量,mi為半球諧振子第i次諧波質量。

2 半球諧振子諧波質量缺陷有限元仿真分析

根據半球諧振子諧波缺陷的分布,建立三維模型,利用有限元數值模擬仿真半球諧振子1～4次的諧波缺陷。針對不同諧波缺陷質量變化,分析諧振子不同諧波缺陷的振型、固有頻率、頻差等的變化趨勢。

半球諧振子采用熱膨脹系數低、化學穩定性能好、品質因數高的熔融石英材料,材料特性參數如表1所示。

表1 諧振子材料特性Table1 Material properties of harmonic oscillator

2.1 半球諧振子一、二、三及四次諧波質量缺陷分析

根據圖1所示的半球諧振子結構,忽略球殼與小柱的倒角,建立一、二、三及四次諧波缺陷的三維模型,如圖3所示。四類諧波缺陷質量差分布形式如圖4所示,質量差的表達式如表2所示。

表2 諧振子一、二、三及四次諧波缺陷質量差表達式Table2 Expression of mass difference on harmonic oscillator1st,2nd,3rd and4th harmonic defects

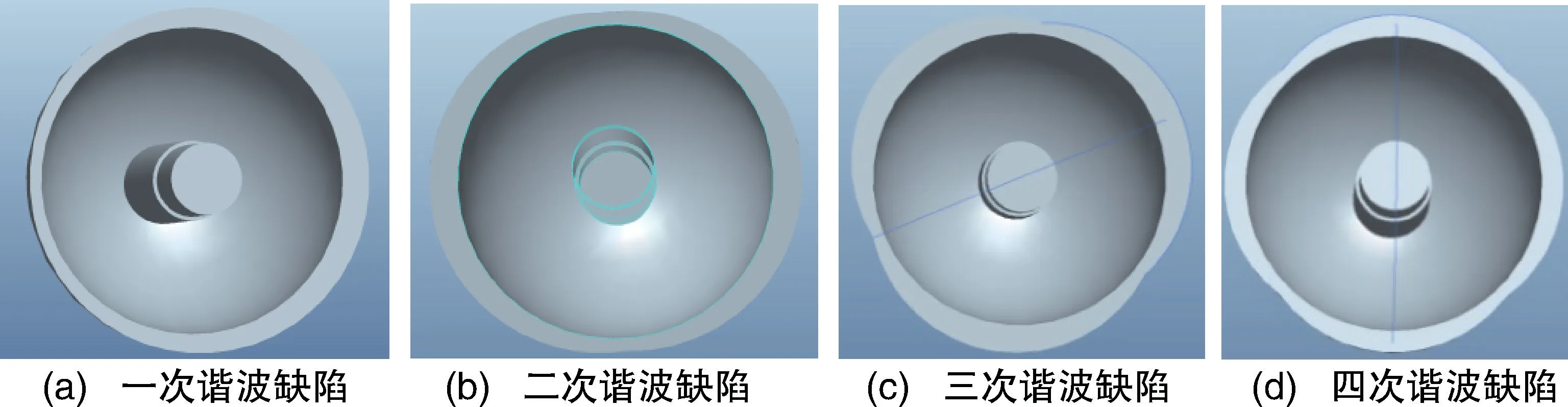
圖3 諧振子一、二、三及四次諧波缺陷三維模型圖Fig.3 Three dimensional model of harmonic oscillator1st,2nd,3rd and4th harmonic defects

圖4 諧振子一、二、三及四次諧波缺陷質量差分布示意圖Fig.4 Mass difference distribution of harmonic oscillator1st,2nd,3rd and4th harmonic defects

R0為半球諧振子外球殼半徑,R1、R2、R3、R4為半球諧振子外橢球殼半徑,Δ1、Δ2、Δ3、Δ4為半球諧振子質量偏差值。在進行半球諧振子諧波質量缺陷分布有限元仿真分析時,質量偏差值Δ1、Δ2、Δ3、Δ4取值范圍為0.01mm～0.1mm。

有限元模型采用四面體單元劃分網格,邊界條件為:在諧振子小柱安裝面施加周向固定約束,以一次諧波缺陷為例,如圖5所示。

四類諧波缺陷有限元仿真結果的振型變化基本一致,以一次諧波為例,有限元仿真結果的諧波缺陷振型變化如圖6所示。

對圖6進行分析,四類諧波缺陷前十階振型模態為:一、二階振型為諧振子左右搖擺模態,三階振型為諧振子拉伸壓縮模態,四、五階振型為四波腹工作模態,六、七階振型為諧振子圓柱搖擺模態,八、九階振型為六波腹模態,十階振型為諧振子半球上下振蕩模態。

利用有限元仿真,通過改變半球諧振子的四類諧波缺陷質量,分析半球諧振子四類諧波缺陷前十階固有頻率與半球諧振子質量的變化關系,如圖7所示。

通過對圖7進行分析,可以得到以下結論:

1）半球諧振子一、二、三及四次諧波缺陷的固有頻率與諧振子質量呈線性關系,四、五階（四波腹模態）及八、九階（六波腹模態）的固有頻率隨著半球諧振子質量增大而增大,其他階固有頻率隨質量增大而減小。

2）各階次諧波缺陷四、五階（四波腹模態）與八、九階（六波腹模態）的固有頻率與質量呈線性比例關系,固有頻率增速隨質量的增加基本一致。

對半球諧振子一、二、三及四次諧波質量缺陷的振動特性進行有限元仿真,其頻差與質量差的關系如圖8所示。

通過對圖8進行分析,可以得到以下結論:

1）半球諧振子四次諧波缺陷頻差與質量差的關系,隨著半球諧振子質量差的增大,頻差逐漸增大,質量差與頻差呈線性關系,關系式為:Δf=1779.5Δm,符合文獻［7］中的公式:Δw=w2-w1=λ?M。

2）半球諧振子二次諧波缺陷頻差與質量差的關系,隨著半球諧振子質量差的增大,頻差逐漸增大,質量差與頻差呈線性關系,關系式為:Δf=536.57Δm,頻差與質量差的增速為四次諧波缺陷的1/3,對頻差影響較大。

3）半球諧振子一、三次諧波缺陷頻差與質量差的關系,隨著質量差的變化,頻差基本沒有變化。

綜上所述,由圖7和圖8可知,半球諧振子二、四次諧波缺陷分布對諧振子振動頻差影響較大,進一步分析二、四次諧波缺陷的質量分布在不同周向及徑向位置時對半球諧振子頻差的影響。

圖7 一、二、三及四次諧波缺陷十階固有頻率與質量關系圖Fig.7 Relationship between tenth order natural frequency and mass on harmonic oscillator 1st,2nd,3rd and4th harmonic defects

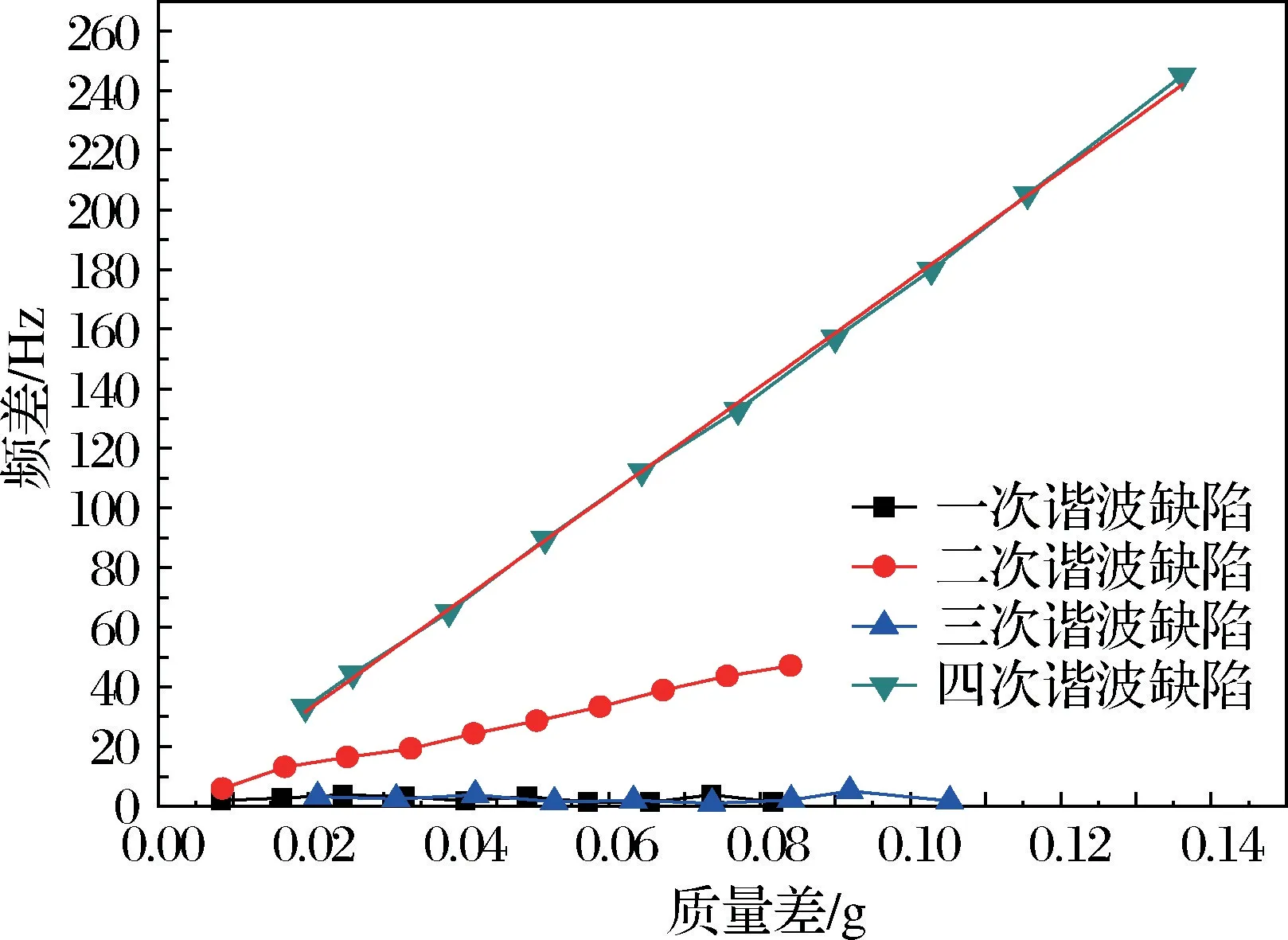
圖8 四類諧波缺陷頻差與質量差關系圖Fig.8 Relationship between frequency difference and mass difference on four types of harmonic defects

2.2 半球諧振子二、四次諧波缺陷沿周向及徑向分布對頻差的影響

根據2.1節的半球諧振子一、二、三及四次諧波缺陷分析可知,半球諧振子二、四次諧波缺陷質量差變化對諧振子頻差有影響,研究二、四次諧波缺陷質量差在半球諧振子周向及徑向對諧振子頻差變化的影響。

圖9（a）為半球諧振子周向張角ε變化的模型圖,圖9（b）為半球諧振子徑向張角θ變化或距Z軸距離變化的模型圖。

根據圖9（a）、圖9（b）所示半球諧振子二、四次諧波缺陷周向及徑向的位置變化,建立半球諧振子三維模型。然后,通過有限元計算,分析質量差沿半球諧振子周向張角ε變化對頻差的影響以及質量差沿半球諧振子徑向張角θ變化（或距Z軸距離變化）對頻差的影響,結果如圖10所示。

圖9 二、四次諧波缺陷質量差沿周向和徑向分布模型圖Fig.9 Circumferential and radial distribution model of2nd,4th harmonic defects mass difference

通過對圖10進行分析,可以得到以下結論:

1）由圖10（a）可知,半球諧振子質量差沿周向張角ε越小,頻差/質量差越大。當質量差沿周向張角大于65°時,質量差沿周向張角變化對諧振子頻差/質量差的影響不顯著。

2）由圖10（b）可知,半球諧振子在相同質量差情況下,質量差的位置如圖8（b）所示,距Z軸距離越大,頻差越大,或沿徑向張角θ越小,頻差越大。當質量差分布距Z軸距離小于8.5mm或沿徑向張角大于40°時,質量差在徑向上的位置變化對諧振子頻差的影響不顯著。

圖10 二、四次諧波缺陷質量差沿周向和徑向分布對頻差的影響Fig.10 Influence of2nd,4th harmonic defects mass difference along circumferential and radial distribution on frequency difference

3）由圖10（a）和圖10（b）可知,半球諧振子二、四次諧波質量缺陷周向張角及徑向位置變化對頻差/質量差的影響曲線基本一致。諧振子質量差在同一張角下或同一徑向位置下,二次諧波缺陷頻差大致為四次諧波缺陷頻差的1/2。

本節分析了二、四次諧波質量缺陷與頻差的關系,為半球諧振子頻差的修正提供了參考,采用機械調平、化學調平、激光調平、離子束調平等方法,可以對半球諧振陀螺不同諧波質量缺陷引起的頻差進行修正,后續研究重點為半球諧振子調平技術。

3 結論

本文對半球諧振陀螺不同諧波質量缺陷分布建立相應三維模型并進行有限元計算,研究了半球諧振子不同諧波質量缺陷的振型、固有頻率、頻率裂解等的變化,分析了半球諧振子質量缺陷沿周向和徑向分布對振動特性的影響,得到以下結論:

1）通過對四類諧波缺陷十階固有頻率的有限元分析,有:諧振子四波腹模態、六波腹模態固有頻率隨諧振子質量增大而增大,且增速基本一致,其他階固有頻率隨質量增大而減小。

2）研究了四類諧波缺陷質量與頻差的關系,其中的二、四次諧波缺陷質量對頻差有明顯影響,二者呈線性比例關系,比例系數分別為536.57和1779.5。

3）進一步分析了諧振子二、四次諧波缺陷質量沿周向及徑向分布對頻差的影響,諧振子周向張角ε越小或徑向距Z軸距離越大（或徑向張角θ越小）時,其頻差越大。也就是說,質量差在諧振子殼體邊緣位置對頻差的影響較大。

基于半球諧振陀螺的有限元仿真,本文對半球諧振陀螺不同諧波質量缺陷分布振動特性進行了研究,為后期開展半球諧振陀螺調平關鍵技術研究提供了參考,具有一定指導意義。