基于局部保持投影的混沌時間序列 降噪方法研究

陳 寧，何 新，吳智群

（西安熱工研究院有限公司，陜西 西安 710054）

隨著火電廠智能化改造的推廣，各種機器學習算法廣泛應用在生產現場。數據清洗作為其流程中不可或缺的第一環，是對分散控制系統（DCS）測點監測原始數據的處理，一般包括對異常點剔除、對缺失點擬合、對含噪數據序列降噪和整體關聯性的排查等，即盡可能地剔除各種干擾，保證其干凈且可靠，這樣才能使算法應用結果更加準確可靠。

火電機組主要由燃燒系統、汽水系統、電氣系統和控制系統4大單元組成，生產流程中伴隨著燃料化學能、蒸汽熱能、機械能及電能之間頻繁轉換。從發電側來看，火電機組關聯龐雜的大型機電設備，宏觀上可認為是一個分布式的復雜機電系統[1]。機組DCS測點得到的監測序列，受復雜工況的影響夾雜著各種噪聲，使其看似無規則，實則卻是非線性確定性系統產生的隨機性波動，經Poincare截面法定性分析，認定是具有混沌特性的一維時間序列[2]。對于混沌時間序列的處理通常要放到相空間中進行[3]，相空間重構技術（phase space reconstruction，PSR）能夠有效重建拓撲意義上等價的原動力系統高維相空間，根據Takens等人提出嵌入定理，m維嵌入相空間與原d維混沌時間序列間的約束條件為m≥2d+10[4]，結合混沌吸引子的低維特性，原機電系統大多是低維動力學系統，產生的有用信號通常局限在低于d維的子空間[5]，而噪聲信號則借由高維動力學系統區別于有用信號，分布在高于d維的子空間。降噪處理就是通過降維使位于高維空間中的噪聲信號被剔除，僅保留低維空間上的有用信號。現有的非線性降維方法主要有核方法和流形學習方法，前者用核函數進行內積運算，后者在流形中尋找嵌入[6-7]。考慮到“樣本外”（out of sample）問題，許多流形學者開始使用從高維到低維的線性映射[8-9]，局部保持投影（locality preserving projection，LPP）建立在將拉普拉斯特征映射線性化的基礎上，但這又會引入混沌時間序列在流形中的非線性特性無法保留、鄰域內最小化局部相似度后投影重合等問題[10]。

為此，本文采用余弦距離推導歐拉表示代替歐氏距離，并在投影時加入正交條件，旨在借鑒核函數降維方法保留原始數據流形中的非線性特性，通過分散臨近點投影解決鄰域內投影過密集問題，消除它們之間的信息冗余，同時又能兼顧局部和全局的幾何特性[11-14]，幾乎不需要先驗知識。采用洛倫茲信號（加入噪聲）進行仿真實驗，結合不同工況下火電機組DCS測點信號進行實例驗證，并與小波降噪、局部保持投影降噪比較，通過分析信噪比（SNR）、最大Lyapunov指數、頻譜及相圖證明本文降噪算法的泛化性和優越性，套用到磨煤機狀態分析算法進行數據清洗證明其即時性和精確性。

1 基礎理論

1.1 局部保持投影

對于流形M上n維原始數據集X=[x1,x2, …,xm]∈Rm×n，其中xi∈Rn是第i個n維原始數據，局部保持投影就是通過一個投影方向矩陣Al×n，把n維原始數據集（高維）映射為l維子空間（低維，l?n）Y=[y1,y2, …,yl]∈Rl×n，使得yi=ATxi[15]。首先構造一個稀疏、對稱的權重矩陣Wij：

接著最小化目標函數S(A)：

可簡化為：

約束條件tr(ATXDXTA)=1，利用拉格朗日乘子法求最小值：

1.2 余弦距離的歐拉表示

對于任意給定的2個向量xi、xj∈Rn，它們之間的余弦距離定義為：

式中：xi(k)、xj(k)分別代表向量xi、xj的第k個分量。 在歐拉表示下轉換為歐幾里得距離形式[17-19]：

2 混沌時間序列降噪方法

2.1 相空間重構

坐標延遲法通過嵌入維數m和時間延遲τ來構造一維時間序列{x(n)}的m維相空間矢量：

時間延遲τ可以通過互信息法來選取，如果τ值選取的太小，則會使得相空間中坐標分量上過于接近，造成各種距離上難以區分地相似，過密集被當作堆疊或是冗余做修正處理；如果τ值選取太大，便會使得相空間中坐標分量上分割開來，毫無相關性可言，丟失原始一維時間序列的混沌特性。由信息論可知，對于時間序列X=[x1,x2, …,xm]和Y=[y1,y2, …,ym]，其信息熵可表示為：

結合互信息函數I(X,Y)=H(x)-H(X|Y)可推得I(X,Y)為：

套用到一維時間序列中{x(n)}及其延遲序列{x(n+τ)}中，顯然互信息是關于τ的函數其值越小所表達的含義是二者在鄰域內最大程度地不相關，于是選取任意小區間中讓I(X,Y)達到極小值時對應的τ值作為延遲時間。

嵌入維數m可以通過偽最近鄰點改進的Cao方法選取，如果m值選取的太小，混沌吸引子會產生堆疊甚至自相交，與原始吸引子在拓撲意義上相去甚遠；如果m值選取的太大，各種混沌不變量會相應地增大計算復雜度，同時放大噪聲的影響，丟失部分原始混沌時間序列的幾何特性[12]。將m維中最近鄰點距離與m+1維進行比較：

在理想化的情況下，一維時間序列隨著嵌入維數m的增大，E(m+1)/E(m)總能在達到飽和后趨于平穩從而得到最佳嵌入維數m的取值，然而在實際混沌時間序列下需要加入補充判斷準則E*(m)：

混沌時間序列內部相關性會使E*(m+1)/E*(m)隨嵌入維數m產生變化，便于確認是否達到飽和。

2.2 流形學習

使用余弦距離的歐拉表示替代歐氏距離會涉及復數域，且在投影時加入了正交條件，故局部保持投影中求取目標函數最小值S(A)min及對應投影方向矩陣應作相應改動：

約束條件為i≠j時

本文降噪算法流程如圖1所示。

由圖1可見，降噪算法具體步驟為：

步驟1將重構的混沌時間序列m維相空間中向量映射到歐拉表示的復雜空間中去，記為。

步驟2利用式(1)及(6)求出權重矩陣W。

步驟3通過定義對角矩陣代入L=D-W計算拉普拉斯矩陣L。

步驟4選取矩陣最小特征a1值λ1所對應的特征向量a1作為投影方向向量，迭代出矩陣再次從最小特征值λ2入手求出其特征向量a2作為投影方向向量[14,17]，重復上述步驟，依次類推直至得出投影方向矩陣A。

步驟5完成嵌入yi=ATxi實現降維。

3 仿真實驗

洛倫茲系統是典型的混沌動力學系統，可用來仿真混沌時間序列進行降噪實驗[13]，在加入高斯白噪聲后分別使用小波降噪、局部保持投影和本文算法實現降噪，通過比較分析時域波形、相空間軌跡及信噪比（ξSNR）來驗證降噪效果。

洛倫茲方程為：

分析圖2—圖5，通過對比時域波形與相空間軌跡可以看出：小波降噪使得含有噪聲的洛倫茲信號變得平整，相空間軌跡也在一定程度上得以修復，高頻噪聲雖有消除，但仍舊含有部分低頻噪聲；使用局部保持投影進行降噪后，相空間整體流形結構上修復較好，卻損失了原系統內的非線性特性且沒能有效抑制高頻部分噪聲；本文算法降噪后相空間整體流形結構基本上與原混沌動力學系統相符，非線性特性也有所保留，對低頻和高頻部分的噪聲均實現了有效抑制，緩和了局部保持投影線性降維過程中的過密集問題。

表1為不同降噪方法降噪效果對比。采用信噪比ξSNR及均方誤差σMSE2個指標來定量衡量3種算法降噪的效果。其中，信噪比反應了消除噪聲還原有用信號的能力，信噪比越大有用信號相對噪聲強度來說占比越高；均方誤差表征了對原動力學系統流形的修復能力，均方誤差越小整體流形結構越平穩。由表1可見：小波降噪側重于消除高頻部分噪聲，對系統的流形結構沒有較好的修復作用；局部保持投影在降維過程中剔除了高維空間中的噪聲，僅保留低維空間上的有用信號，可以有效平整混沌動力學系統的流形結構，卻無法抑制高頻部分噪聲，原系統內的非線性特性也沒能保留，在ξSNR= 15 dB的環境中降噪表現甚至略遜于傳統的小波方法；而本文方法借鑒了核函數降維特點，對非線性特性加以保留，且通過新的距離定義分散臨近點投影，保持局部和全局的幾何特性，降噪效果在流形和頻域上均有提高。

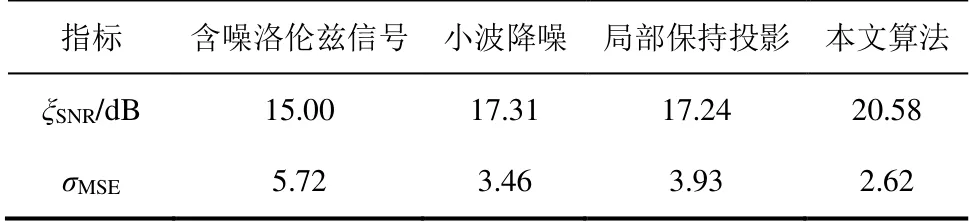
表1 不同降噪方法降噪效果對比 Tab.1 Comparison of SNR values before and after noise reduction for different noise reduction methods

4 實例應用

4.1 降噪方法的泛化性與有效性

采用華能某電廠600 MW發電機組DCS監測數據驗證算法的泛化性與有效性，選取不同工況測點數據（表2）：工況1為機組負荷372.95 MW，主蒸汽溫度為538.11 ℃；工況2為機組負荷為 536.27 MW，主蒸汽壓力為25.71 MPa；工況3為機組負荷223.31 MW，小汽輪機A軸向位移0.06 mm；工況4為機組負荷468.18 MW，脹差3.96 mm。

表2 DCS采集監測序列 Tab.2 DCS collecting and monitoring sequence

分別用小波降噪、局部保持投影和本文方法進行降噪處理，對比相空間二維相圖、低頻及高頻域降噪效果，選取混沌特性較為顯著的工況3測點時間序列信號降噪處理前后情況進行展示（圖6）。在相空間重構階段由互信息法得出τ=4，Cao方法得出嵌入維數后向下取值得到最大整數m=6。在降維階段利用G-P法計算關聯維數直到下降變緩停止迭代，最終得出本征維數達到最佳降噪效果。

Lyapunov指數通常只需要簡化為計算最大Lyapunov指數就可以用來表征一個動力學系統的混沌特性，在對初值敏感的前提下，Lyapunov指數通過衡量相空間中運動軌跡的指數式離散描述混沌特性，混沌吸引子在此基礎上不斷折疊發散，形成復雜結構。選取最大Lyapunov指數作為定量研究相空間混沌不變量的指標，其值為正數表示序列具有混沌性，其值越大，代表著混沌特性越強烈。圖7為DCS信號經過不同方法降噪前后的最大Lyapunov指數，圖8為工況3測點經過不同方法降噪前后的頻譜圖，圖9為經不同方法降噪前后的信噪比。由圖8可見，原始信號在低頻段內15 Hz附近及36.4 Hz處有較為明顯的噪聲分布，高頻段內212.9 Hz處存在噪聲分布。

對比3種方法降噪后的頻譜：小波降噪屬于帶通濾波，能過濾掉高頻噪聲，但對于低頻噪聲則效果微弱且會對有用信號產生抑制效果；而局部保持投影更注重對整體動力學流形結構的修復，有一定的去噪能力，但同樣對有用信號產生了負面的抑制效果，甚至未有效消除高頻段內212.9 Hz處噪聲；本文方法不僅能消除高頻噪聲，還會在處理低頻噪聲時一定程度上保留更多的有用信號，這一結論也在圖9中對信噪比的定量計算得到印證。

局部放大圖6，觀察二維相圖整體流形結構的平整程度和對原動力學系統的修復能力，結合圖7中通過最大Lyapunov指數定量對比的混沌特性（包括非線性、內隨機性等），不難看出傳統的小波降噪幾乎不具備流形學上的修復能力；局部保持投影已經能有效讓結構雜亂無章的相空間一定程度上變得清晰平整，對原動力學系統流形結構起到修復作用；而本文方法進一步讓相空間軌跡變得光滑，并保留了原本混沌時間監測序列內在特性（如非線性等）。整體而言，本文降噪方法在頻域及流形上，不僅能夠較好地修復相空間整體流形結構，使其變得清晰、平整、光滑，在過濾掉高、低頻噪聲的同時還能更多地保留有用信號及非線性特性。

4.2 工程應用

對珠海某熱電公司磨煤機狀態分析時采用 長短期記憶（LSTM）神經網絡。選取數據樣本 103 680組，按照10折交叉驗證完成模型的訓練與測試，直接使用原始數據D0、清洗工具箱處理數據D1及本文降噪算法處理數據D23種情況下以準確率及耗時作為指標評價。圖10和圖11分別為不同數據清洗方法時模型準確度和耗時對比。由圖10和圖11可見，增加數據清洗環節使訓練的LSTM神經網絡在預測準確率上有較顯著提升，本文降噪算法進行數據清洗又比通過清洗工具箱清洗數據得到神經網絡模型準確度更高，模型運算速度更快。

5 結 語

本文在局部保持投影算法對DCS數據進行降維去噪的基礎上，采用余弦距離推導出歐拉表示替代歐氏距離，并在投影時加入正交條件，旨在借鑒核函數降維方法保留原始數據流形中的非線性特性，通過分散臨近點投影解決鄰域內投影過密集問題，消除信息冗余。將本文算法與傳統小波降噪、局部保持投影進行對比分析，從流形和頻域兩方面驗證效果。仿真和實際應用結果表明，本文算法能夠較好地修復相空間整體流形結構，還原混沌動力學系統的拓撲結構，對低頻和高頻部分的噪聲均實現了有效抑制且能夠保留原始信號非線性特性，從預測結果的準確率和耗時兩方面證明了本文降噪算法在數據清洗時的優越性。