追根溯源探本質 變式拓展提能力
——一道三角函數圖象與性質真題的本質與變式研究

廣東 雷雄軍 朱廣智

(作者單位：東莞市第六高級中學)

三角函數作為基本初等函數，是高中數學的一個重要內容，也是高考考查的熱點模塊.筆者研究2019—2021年高考全國卷發現，此模塊知識主要以小題形式考查，通常一道客觀題或者兩道客觀題，難度中等偏易.同時也發現三年中加強了對三角函數圖象與性質的考查：如2021年全國乙卷理科選擇題考查了三角函數圖象的變換；2021年全國甲卷填空題考查了三角函數的性質；2020年高考全國卷Ⅰ理科考查了三角函數的圖象與性質；2019年高考數學全國卷Ⅰ，卷Ⅱ理科選擇題都考查了三角函數的圖象與性質.筆者在教學過程中發現學生對三角函數圖象變換中常見的“先平移后伸縮”和“先伸縮后平移”兩種類型題目不能很好地作答.主要根源還是教師在平常的教學中沒有注重知識本質的講解，不會進行恰當的變式，化多為少，以一當十，讓學生觸類旁通，舉一反三.現以2021年全國乙卷理科選擇題第7題為母題，探究三角函數圖象變換的本源，即通過四個恰當的變式，幫助學生鞏固所學的知識，提升學生的解題能力和思維能力.

一、母題的選取及分析

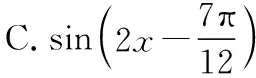
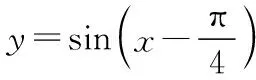
故選B.

課堂給學生做的過程中發現有部分考生出現了以下的錯解：

二、母題本源深入探究

出現上面的錯解的源頭就是未能對函數y=Asin(ωx+φ)+b中參數ω，φ的意義理解透徹.舊教材中只對四個字母的幾何意義進行了解釋，A變換的幾何意義是縱坐標的伸縮變換，ω變換的幾何意義是橫坐標的伸縮變換，φ變換的幾何意義是圖象的左右平移，b變換的幾何意義是圖象的上下平移.但是幾何意義理解比較抽象，學生掌握起來比較困難.新教材在此章節上對函數y=Asin(ωx+φ)安排了專門的一小節內容，繞開了抽象的幾何意義而是從具體的物理意義的角度解釋A,ω，φ,b，x,y這六個變量，學生掌握起來比較容易.新教材以古代的一種水利灌溉工具筒車為具體背景，抽象出數學模型如圖所示：

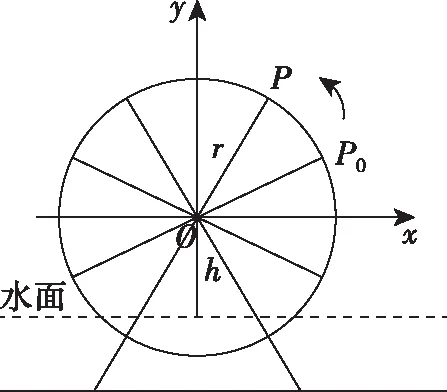
得到盛水筒P距離水面的高度H與時間t的關系式：H=rsin(ωt+φ)+h，r的物理意義是振幅即筒車的半徑，ω的物理意義是筒車旋轉的角速度，t的物理意義是運動的時間，φ的物理意義是盛水筒的初始位置，h的物理意義是筒車中心到水面的距離.由正弦函數圖象y=sinx變換到函數y=Asin(ωx+φ)+b圖象過程中，學生理解的難點在參數的ω，φ變換上.下面從物理意義直觀理解先變φ后變ω與先變ω后變φ的區別(假定ω>0,φ>0).

先變φ后變ω：

=sin(ωx+φ)

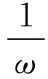
先變ω后變φ：

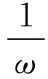
三、母題的變式拓展探究

有了上述對參數的具體物理意義的理解，學生對這個題目可以輕松解答.我們都知道高考真題是經典的數學試題，為了發揮其應有的價值，在教學過程中我們就要注重對其進行變式拓展延伸，這樣不僅能夠幫助學生深入理解要學的知識，還有助于培養學生靈活的思維方式，培養學生的求異思維，創新能力，提升學生的應變能力，讓課堂教學成為真正的高效課堂.筆者從以下四個方面對此題進行了變式.

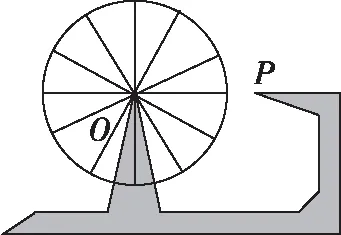
變式一：如圖，一個摩天輪的半徑為10米，輪子的最底部距離地面2米，如果此摩天輪按照逆時針轉動，每4分鐘轉一圈，且當摩天輪上某人經過點P處(點P與摩天輪中心高度相同)時開始計時，則經過1分鐘后此人相對地面的高度為______米；在摩天輪轉動一圈內，此人相對于地面高度不低于17米的時間為________秒.

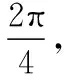
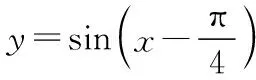
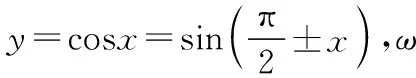
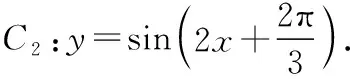
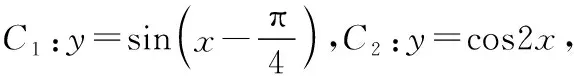
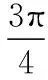
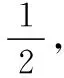
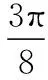
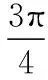
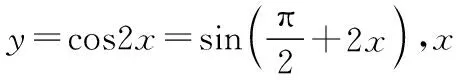
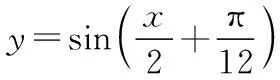
四、結語

變式教學在數學課堂教學中具有非常重要的意義，上面由一個看似簡單的三角函數圖象變換的高考真題出發，通過對其參數具體物理意義的本源探究，及其對題目多角度層層遞進的變式探究，有效地深化了對三角函數圖形變換知識的理解與掌握，突破了三角函數圖形變換中的難點，開拓了學生的解題思維，有效促進了學生思維品質的改善和創新能力的提升.盡管高考試題不斷地推陳出新，但其原型還是來源于我們的教材，來源于我們平時做的習題，所以我們教師在平時的教學過程中，要注重對學生所學的知識點，所做的題目進行有目的的變式訓練.新授課時，變式教學要注重對情境問題進行變式探究，如本課試題可以將筒車變式為學生熟悉的摩天輪，然后設置相關問題，通過情境問題變式，增加學生對問題的思考，進而更好地理解即將要學的新知識.習題課時，對題目的變式要注重立足于原有的題目(不能脫離原有的題目)，通過對題目中的條件、結論多角度、多視角切入變式探究，真正做到“一題多思”“一題多問”“一題多變”.巧妙地把題目中豐富的知識底蘊充分挖掘出來，形成一個有效的知識網絡體系，真正提升學生解題能力，拓展數學應用.