五年制高職數學“活動單導學”教學模式研究

殷冬美

(江蘇省泰興中等專業學校 225499)

隨著新課程改革日益深入，基于自主探究理念的教學模式不斷被創新，并為高等教育的知識技能傳授提供了更多可能性.比如江蘇省如皋市創新的“活動單導學”教學模式，目前已在各級各類學校的各學科教學中廣泛應用，并取得了較理想成效.

1 “活動單導學”概念

“活動單導學”是依據課程目標編排“活動單”，利用多種“活動”引導學生自主參與課程內容學習，獲得知識與技能，確保教學目標有效落地的模式.其主要包含三大基本要素，一是“活動”，包括社會實踐活動、靜態思維活動等能敦促學生主動獲取教學內容的各類型活動；二是“活動單”，重在明確教學目標、教學內容以及教學活動的具體實施方案；三是“導學”，是教師設計情境、點撥啟發、適度評價以指導學生自主學習的過程.整體來看，“活動單導學”是圍繞活動進行的教學模式.

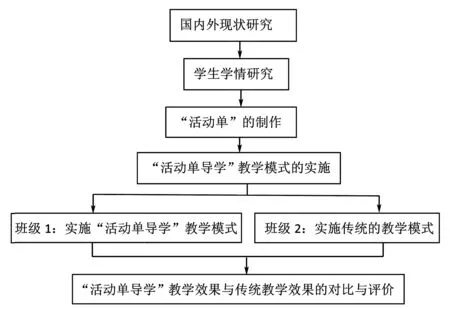
2 “活動單導學”研究思路

3 “活動單導學”的創新之處

第一，有利于學生的自主學習.在傳統的高職數學教學過程中，課堂起著全程主導的作用，使得學生一離開課堂就容易脫離學習環境.在“活動單導學”教學模式中，教師授課時間會越來越少，目的是促進學生通過自身的反思，逐步學會自主學習，這樣，即便教師課堂授課時間較少，也不會影響到學生的學習，反而會學到更多.

第二，活動單導學”教學模式有利于個性化的學習.高職數學既是一門知識，也是一種技能.高職數學教學目的是激發學生的學習熱情，培養學習興趣，樹立自信心，培養好的學習習慣，發展學習能力、團隊精神.學生需要通過大量思考和實踐，才能更好地掌握高職數學.“活動單導學”教學模式在一定程度上解決了學生在學習過程中的知識和技能方面的短缺，真正培養了學生的綜合素質.

4 五年制高職數學應用“活動單導學”教學模式的可行性

4.1 激活數學潛能

“活動單導學”教學模式突破了以課堂、教師或教材等為中心的傳統教育模式的局限，歸還了學生主體地位，強化了數學學科教師的教學指導功能，使高職學生得以通過參與活動不斷激發內在數學潛能，豐富高職數學知識與技能，形成更完善的高職數學知識結構，實現個人能力成長.

4.2 促進全體學習

“活動單導學”教學模式下的五年制高職數學課堂是一種開放性課堂，不同個性、不同學業水平的高職生均能參與力所能及的數學問題分析、解決活動，調動自身的視覺、聽覺、觸覺等感官感知數學實際，深刻記憶數學內容，進而培育起數學思維，養成數學自信，更積極主動地參與數學學習與應用.

4.3 培育綜合思維

“活動單導學”教學模式下，“活動”貫穿了高職數學課程的每一個環節，使數學內容由抽象轉化為了具象，便于高職生理解并掌握.同時，因“活動”不僅涉及數學學科知識，還包含其他學科知識，學生參與活動時或能體會各學科的橫縱聯系，不斷完善自身的綜合知識應用思維.

5 五年制高職數學“活動單導學”教學模式的建設

根據“活動單導學”概念，基于“活動單導學”的高職數學教學模式必然有其“活動單”、“活動”以及導學過程.為更具體地探討這三大要素，下文以《等比數列》為案例進行深入分析.

5.1 梳理《等比數列》課程要點

[學習目標]

(1)了解、掌握等比數列的基本定義；

(2)掌握等比數列通項公式、推導方法、推導過程；

(3)應用等比數列通項公式處理數學問題.

[教學重難點]等比數列基本定義、通項公式、推導方法及應用.

5.2 設計并執行教學過程活動單

【課前預習單】相比中職生，高職生的數學智力相對更高.若其能養成良好的數學學習習慣，比如提前預習新課，則其數學知識學習效率將有所提高.因此，應用“活動單導學”模式開展數學教學時，須先設置“預學活動單”.根據《等比數列》的學習目標、教學重難點，本文設計如下“活動”：

學生自主學習，回顧等差數列基本定義、通項公式、推導方法、公差確定方法，嘗試用類比方式預習《等比數列》的內容.

【課堂探析單】活動一：復習接龍

課前5分鐘，抽查預學狀況.邀請4位學生，以復習接龍的方法，逐一復習等差數列基本定義、通項公式、推導方法、公差確定方法.

此活動重在鞏固學生的等差數列知識，并為等比數列概念學習提供切入口.

活動二：小組討論

依照“同組異質、異組同質”原則，結合班級學生的數學學習能力，將全班學生劃分為4-6人一組.要求同組成員共同討論并解決問題.小組劃分結束，出示以下4組等比數列，要求學生參與小組討論，觀察個中特點.

(1)-2、1、4、7、10、13、16、19……

(2)1、1、1、1、1、1、1、1……

(3)1、2、4、8、16、32……

(4)8、16、32、64、128、256……

提供10分鐘小組討論時間.小組討論過程中，數學老師逐組巡視，為沒有思路的小組指導觀察方向，與已經發現數列特點的學生交流，聆聽其發現過程，及時指出其錯誤之處，表揚其正確之處.10分鐘討論時間結束后，邀請各小組選派代表，按順序說出本組的發現.

活動三：視頻直觀

各小組代表逐一說明上述四個數列的特征后，由數學老師主導播放等比數列的實際生活案例，比如細胞分裂案例：1個細胞分裂為2個細胞，2個細胞分裂為4個細胞……在視頻播放過程中，邀請各組學生記錄每個單位所分裂的細胞數量.待視頻播放結束，請一組學生到黑板上寫下細胞在各單位時間的分裂數量，并提煉出其中的共同特性.

隨后，以數學老師為主導，組織全班學生結合案例，回歸教材，總結等比數列的定義：如果一個數列從第二項開始，每一項與其前一項的比都為同一常數，那么此數列即是等比數列，常數即是數列公比.

同時，基于等比數列定義，推導出等比數列的通項公式.

活動四：幻燈片強調關鍵

采用幻燈片滾動方式，逐一出示誤區題，借以強調說明下列四個關鍵問題：

(1)等比數列的第一項絕對不能是0；

(2)等比數列中的每項數字都不允許是0，否則數列不成立；

(3)等比數列的公比絕對不等于0；

(4)非零常數列既為等比數列，又是等差數列.

活動五：編寫數學故事

以上四個關鍵問題提出后，邀請全班學生先花五分鐘獨立思考包含等比數列的數學故事，后花5分鐘進行小組討論，由各組員輪流介紹自己編寫的關于等比數列的數學故事.經過數學故事介紹，小組推選一名代表，向其他同學講解本組公認最好的數學故事，并說明其包含的等比數列.例如古印度宰相與國王下棋，贏棋后請求獲得以下賞賜：以棋盤為局，在第一個格子放1粒麥子，第二個格子放2粒麥子，第三個格子放4粒麥子，第四個格子放8粒麥子……直至第六十四個格子放滿，由此得到公比為2的等比數列.

根據所學知識點編寫數學故事具有較大的難度，它既考驗學生對數學知識的理解能力，又考驗學生的故事創造力.然而，對比以上教學活動，數學故事編寫活動卻能使高職生更快地掌握等比數列等知識點，甚至因此對數學知識產生極大的熱情.因此，在條件允許的情況下，高職數學老師應盡量設計這種創造性的活動.

【課堂檢測單】(1)在等比數列{an}中，a3=2,a5=8,則a1=____,q=____.

(2)在等比數列{an}中，若a1=3,q=2,則a8=____.

(3)在等比數列{an}中，a1+a2=1,a3+a4=9,則a5+a6=____.

5.3 教學反饋與鞏固

依據由淺入深原則設計并執行教學活動單后，高職數學老師還需適當撥冗時間開展教學反饋，幫助學生鞏固所學知識點.例如，應用幻燈片、圖片、黑板板書等方式出示關于等比數列的選擇題、填空題、簡答題等，要求學生快速作答.此時數學老師須注意，要控制出題的難度，重點聚焦基礎鞏固，且檢查反饋時間保持在5分鐘內，避免引起學生的思考疲憊.若時間允許，還可邀請學生提供活動單改進建議，以優化教學模式.

綜上，在后續數學教學過程中，五年制高職數學老師可適度依據課程標準，從數學實際、學生全面發展需求等出發，創新更多類活動，包括數學實驗、數學游戲等以引導學生更積極地參與數學學習，進而激活高職生數學學習興趣與潛能.