公路工程隧道橋梁造價指標
文 / 湖南省交通規劃勘察設計院有限公司 彭杰
建立測算模型的原理
通過分析相關資料可知,公路工程造價和環境因素、施工因素之間具有非確定性關聯,可應用回歸模型對公路工程造價和其影響因素之間的關系進行描述,即基于回歸分析建模方法的線性模型或非線性模型。回歸建模的具體方式為:先分析散點圖,通過分析結果了解變量之間屬于線性或非線性關系,然后建立模型。假設會使參數造價受到影響的因素有P個,則建立的多元線性回歸模型可用公式1表達。
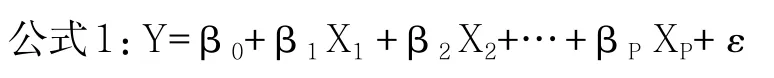
公式中Y表示因變量;X表示變量;β表示參數值;ε表示誤差值。公路工程造價測算新方法:公路工程造價=主線工程造價+互通及服務區造價+隧道造價
公路造價測算模型
主線工程造價測算模型
公路工程主線工程造價及每公里造價指標。利用皮爾遜線性相關系數分析法對以上各項數據展開分析,得出皮爾遜線性相關系數分析結果(如表1所示)。從系數相關大小可以發現,在公路工程造價中對其產生影響最大的造價指標依次是路面、橋梁、長度和路基。

應用對數模型對公路工程主線工程造價值進行計算,計算過程如公式2所示,公式中各項量涵義如表2所示。公式2:主線工程造價=γ×sxp[10.6085+0.1250×log(路基工程量)-0.2865×log(路面工程量)+0.1939×log(橋梁工程量)+0.6962log(其他工程量)]

服務區及互通立交工程測算模型
不同施工環境中互通立交工程的造價差異顯著。如部分平原區互通立交工程造價低于5000萬元,部分山區中互通立交工程的造價可達2億元。通過對比采集數據中互通立交工程和服務區的數量發現,二者數量相當。因此,本文直接將二者數據進行合同統一研究和構建測算的模型。
另外,本文將對該省份已經批復的公路工程造價文件中部分公路互通立交工程的造價信息整理為表3。通過數據分析發現,公路工程互通立交工程造價中,橋梁工程量和路基工程量對總造價的影響最為顯著,其影響程度以皮爾遜線性相關系數表示為表4。


通過現象相關系統可知,山區、平原地區和沿江施工區域中,互通立交工程和服務區工程造價測算關系都可用公式3進行表示。
服務區互通立交造價
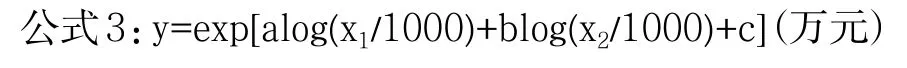
公式中a、b、c在不同施工環境下的參數,具體參數值如表5所示。

隧道造價測算模型
隧道工程多建設在山區環境中,本文采用某省份中部分隧道工程的造價指標作為研究數據進行詳細分析。部分公路工程隧道工程造價指標如表6所示。

將隧道工程造價影響因素選為隧道長度和圍巖類型兩種,以此作為基礎數據進行建模。由于隧道圍巖類型各不相同,將隧道工程造價與圍巖長度、圍巖類型之間的線性相關系數表示為表7。

本文選用7條公路工程中共27條隧道工程的造價數據,經過對比發現,隧道工程造價水平主要受圍堰類別的影響。因此,在分析隧道工程造價影響因素時,將圍堰類別選為變量因素。因二級圍巖的隧道工程施工案例和可搜集數據資料較少,在本文中不將其選為變量參考指標。除圍巖類別外,隧道施工長度是隧道工程施工量的直接體現,所以,最終分析隧道工程的造價影響因素時,將隧道建設長度、Ⅲ、Ⅳ、Ⅴ級圍堰類別作為關鍵變量因素,并以此建立回歸模型。變量因素測算可通過如下公式4完成。
公式4:隧道工程造價=120.5592-1.0512×隧道長度+0.4489×三級圍巖面積+0.5491×四級圍巖面積+0、843×五級圍巖面積 (萬元)
公路工程造價指標測算結果
本文通過選取某省份12個公路工程建設項目造價數據,對公路工程造價過程中各影響因素和造價測算結果進行分析、比對、統計,最終確定以此種測算模型進行工程造價驗算。采用此種測算模型計算后,公路工程造價主要影響因素中主線工程、服務區及互通立交工程、隧道工程和總工程造價的誤差值都在0.1以內,符合我國現行工程造價相關規范的要求,表明該方法具有較好可應用性和準確性。
結語
綜上所述,應用以上三種工程采用針對性的造價評估方法,才能最大化提高公路工程造價測算的準確性,且可充分應用相關系數法非線性或線性回歸法等科學方法,以公路工程造價評估模型進行造價測算,幫助公路建造企業管理人員作出更具科學性的工程決策。

