面向戰備完好的飛機群組預防性維護優化和備件預測方法

李婷， 劉林， 彭云程， 崔超雄， 薛非

(西安飛機工業(集團)有限責任公司， 陜西 西安 710089)

0 引言

為適應新時期飛機高強度服役和快速作戰響應的發展趨勢，部隊實戰化飛行訓練任務加大，飛機維護模式和備件需求不確定性逐漸增加。而信息化和智能化的作戰需求，也對以戰備完好性為代表的各項健康性能指標提出的更高的要求。現有以工程經驗為主導的事后/定期維護機制，和該既定機制下的備件管理方法，缺乏對飛機服役模式和運行狀態的有效兼容，以及對備件需求規律的準確把握，很難滿足裝備發展“科學精準快速保障”的需求。

目前國內外針對以飛機為代表的航空設備預防性維護和備件優化，在定性和定量層面開展了一些基礎性研究工作。定性研究方面，蘇亨鋦介紹了基于測試數據的航空裝備視情維修研究整體思路。鄭志霖介紹了民用飛機維修方案優化的工作項目流程，強調利用可靠性數據的重要性。定量研究方面，根據航空產品性質和用途的不同，可用度和運維成本是維護和備件優化的兩個核心優化目標。Liu針對機身蒙皮采用三階段維納過程模型描述裂紋擴展，對每階段設計不同的檢測周期并優化預防性維修閾值。王華探討了飛機維修控制在民用航空成本控制中的應用情況。楊力研究了復雜串并聯航空系統壽命周期成本的優化算法。而在軍用航空方面，戰備完好性，或者可用度是更加常見的維修保障目標。馬小兵研究了可用度約束下的航空產品壽命建模和優化。涂繼亮等將可用度和保障率作為優化參數，對飛機的備件方案進行優化。陳博等基于DEVS-OODA模型對作戰飛機備件需求進行了定量預測。陳云翔等基于分層賦時著色Petri網構建飛機編隊仿真模型，優化保障資源配置。李巖等則考慮戰時情況下的維護保障人員數量確定問題。然而，目前的研究在實際應用中仍存在一些不夠完善的地方：1)維護方案以事后維護和簡單的年齡維護為主，缺乏針對不同典型失效部件(壽命件、缺陷件、退化件等)構成系統的整體維護規劃調度；2)備件預測技術往往和整機級維護方案脫節，導致不能較好反應飛機當前的維修水平和計劃，導致備件過度或者不足的風險增大。

針對以上的問題，本文以提升飛機裝備保障戰備完好性(服役可用性)為目標，整體研究了飛機群組預防性維護調度計劃建模和優化方法，以及基于既定最優維護計劃的備件需求預測方法。具體地，分別針對典型壽命件和包含缺陷(潛在故障)態的部件，制定相應的個體維護方案，以此為基準安排飛機系統的整體預防性群組維護計劃。通過結合馬爾科夫過程(描述健康狀態轉移)和延遲時間模型(描述缺陷發展特點)，基于更新過程對基準檢修窗口長度和各部件所需窗口數量開展聯合解析優化，實現飛機系統平均可用度最大化。最后基于既定的系統層級最優維護計劃，通過離散仿真算法對規劃周期內的備件需求數量開展預測。對比現有的飛機維護和備件優化方面的研究，本文提出的方法有如下三方面的貢獻：

1) 基于日歷時間的群組維護框架，通過同時設置維護窗口單元，實現了對飛機典型失效件維護計劃的協同規劃，有效避免了維護資源浪費和停機時間過長的問題；

2) 通過高效的解析優化算法，實現了對飛機裝備整機級可用度的快速精確計算，顯著降低了維護規劃的復雜度；

3) 群組維護策略驅動的備件預測技術，相比傳統的純數據驅動方法，能夠更加緊密貼合飛機故障特點和維護方案，反映備件需求的物理統計分布特征。

剩余章節的結構安排如下。第一章介紹飛機裝備維護保障相關問題，包括關鍵組件的故障特點，整體維護策略等。第二章開展面向戰備完好的飛機檢修模型構建和優化工作。第三章基于既定維護優化結果開展飛機備件需求預測的工作。第四章通過數值案例驗證本論文模型方法對提升戰備完好性的有效性。

1 問題描述

1.1 故障特點

考慮飛機裝備的預防性檢修計劃，共覆蓋個關鍵部件分系統。根據歷史故障數據和運行維護記錄，個檢修部件分系統按照失效特點可以分為以下兩類典型結構：1)壽命件；2)缺陷件。

1) 壽命件。壽命件只包含正常態和失效態兩種狀態，其失效時間服從一定的隨機概率分布。典型的壽命件包括非金屬產品，如橡膠密封圈等。壽命件一般可按定期更換處理。所有壽命件集合記為N。

2) 缺陷件。缺陷件的失效過程包括正常態、缺陷態和失效態三種狀態。和壽命件相比，缺陷件在失效前會出現可識別的缺陷(進入缺陷態)。例如，軸承在使用過程中疲勞裂紋逐漸形成和擴展，擴展到一定程度則導致軸承振動信號出現顯著變化。一般地，產品從缺陷狀態到完全失效的時間較短，影響運行安全，因此需要制定檢修計劃盡早發現，一旦發現缺陷則安排維修更換工作。所有缺陷件集合記為N。

1.2 預防性維護和備件策略

根據兩類部件的特點，壽命件進行定期更換，缺陷件進行定期檢修。對于缺陷件，一旦檢測發現缺陷，則立即更換。如果部件在檢測周期內發生失效，則立即更換。相比于年齡維護策略，周期檢修策略產生的維護計劃確定性強，利于實際執行。為簡單起見，本文假設所有部件失效均可立即發現(例如飛行過程中的傳感器指示、飛機日常維護和測試)，并進行修復/更換處理。

所有部件在定期維護時進行的更換稱為預防性更換(PR)，在失效時發生的更換稱為修復性更換(CR)。一般而言，PR是按照既定維護計劃進行的維護活動，確定性強，維護人員和設備可提前就位，因此飛機停機時間較短；CR取決于部件隨機的失效時間，修復時一方面需要等待維護人員和設備就位，另一方面需要復雜的測試以定位故障部件，因此飛機停機時間較長。

部件維護時間可進一步分為兩部分：1)維護固定時間，例如飛機從停機坪到機庫的時間、維護前準備時間和維護后測試時間等；2)各部件專門進行維護的時間，為各部件屬性。其中，維護固定時間是系統屬性，可被所有部件維護時共享，因此考慮將多個部件的維護活動組合到一起，將各部件的更換檢修周期設置為某一基礎周期的整數倍，以共享從而減少飛機停機時間。該類維護策略也稱為成組維護(block maintenance)。

綜上分析，問題設定和飛機維護檢修策略具體為：

1)壽命件進行定期更換；缺陷件進行定期檢測，如果檢測發現缺陷則進行預防性更換；如果某部件在維護周期內發生故障則立即進行故障更換。各部件失效相互獨立；

2)所有部件的更換檢測周期均為其中最短周期的整數倍，該最短周期也稱為基礎周期，記為；

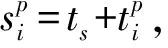
4)當同一時刻多個部件進行維護時，系統維護時間為其中的最大值。任一部件進行維護均導致系統停機。

圖1給出了系統維護策略示意圖。四個部件各自的PR周期或定檢周期為某一基礎周期的整數倍。故障發生則系統停機立即進行修復(如壽命件2)。缺陷件檢測時發現缺陷則立即更換(如缺陷件1在2時刻)，否則只進行檢測(如缺陷件2)。

2 面向戰備完好的維護優化

本節采用兩階段法建立飛機系統維護模型：1)部件級檢修模型：分別根據壽命件和缺陷件的維護策略建立相應的可用度模型，通過最大化可用度確定部件級最優更換檢測周期；2)在部件級模型的基礎上建立系統戰備完好(可用度)模型，然后以部件級優化結果為基礎確定系統級最優維護周期，最后以最大化系統可用度為目標優化系統維護策略。兩階段法的優點是可以解除系統狀態耦合，簡單合理，可以處理規模較大的多部件系統。

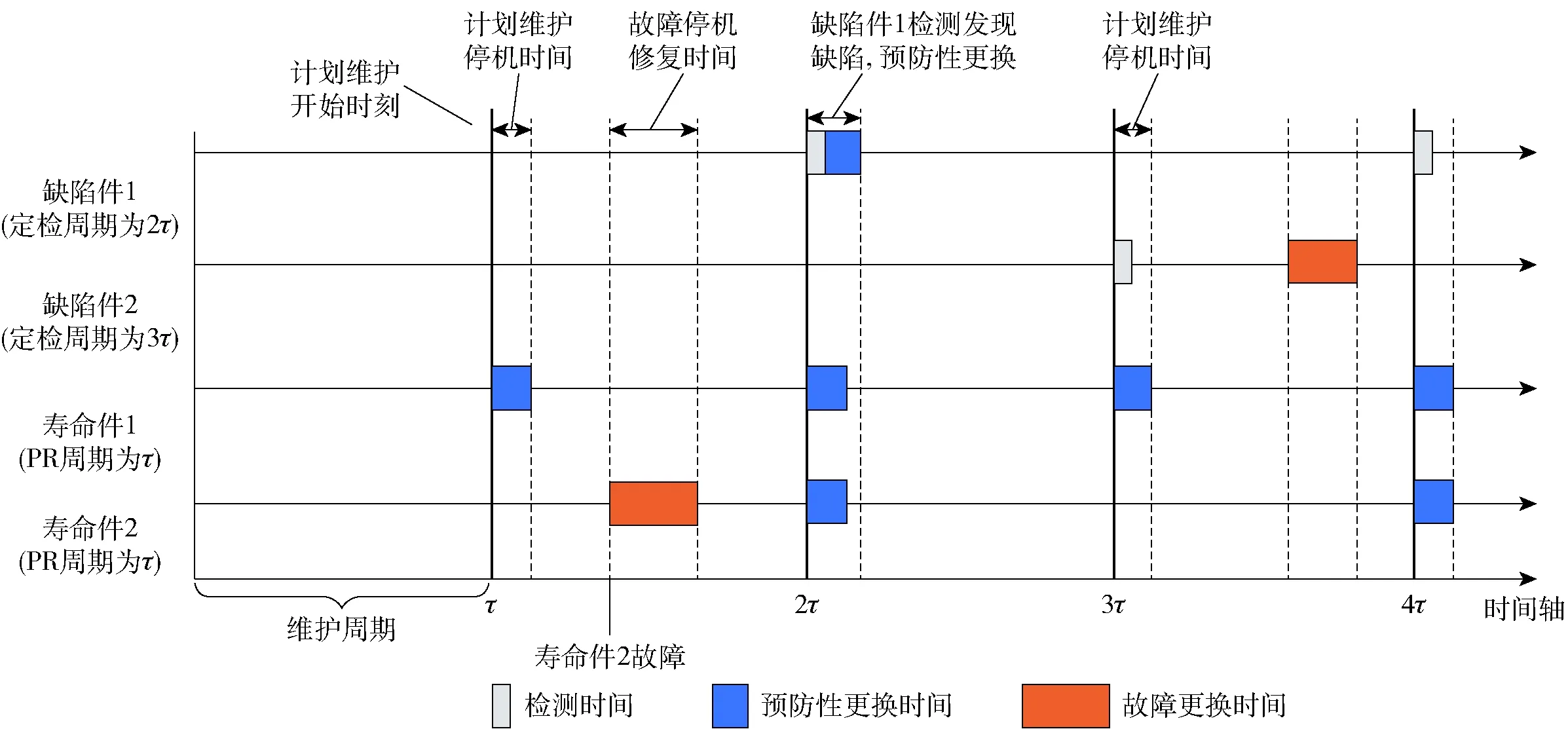
圖1 飛機成組維護策略與停機時間示意圖Fig.1 Diagram of aircraft group maintenance strategy and downtime

2.1 部件級維護建模

211 壽命件

假設某壽命件∈N的失效時間(連續工作時間)分布函數(CDF)為()，若飛機在服役期間的使用率為，則等效于部件∈N的失效時間(日歷時間)分布為()。為簡單起見，省略使用率參數，統一使用()代表折合后的失效時間分布，密度函數(PDF)為()。

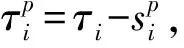
(1)

式中：()表示部件在時間內的失效次數。若忽略一個周期內失效次數超過2次的可能(避免預防性更換喪失意義)，則

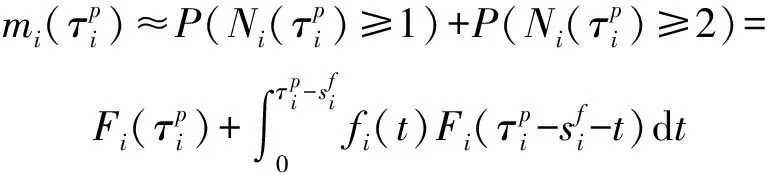
(2)

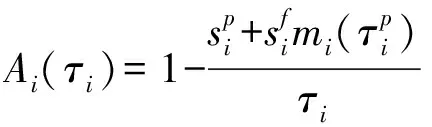
(3)

212 缺陷件

由于缺陷件進行周期檢，檢修后的部件一定處于正常態，以周期檢時間點為觀測點、以處于正常態的年齡為狀態，缺陷件的狀態演化可用馬爾可夫過程建模。為求解穩態平均可用度，需要求解該缺陷件的穩態狀態概率。

記該缺陷件的定檢周期為，令=-，=-，=-。記檢修后部件年齡為0(缺陷更換)的概率為，年齡為的概率密度函數為()，>0。考慮到實際中一個定檢周期內部件失效次數不會太多，因此只考慮一個周期內最多發生一次失效，建立穩態方程。共分為1～4四種情形。

1)1：初始年齡為0(更換后)，周期結束時需要進行PR，轉移概率為(0|0)

如果部件在周期內發生失效(一次)，則該情況的轉移概率為

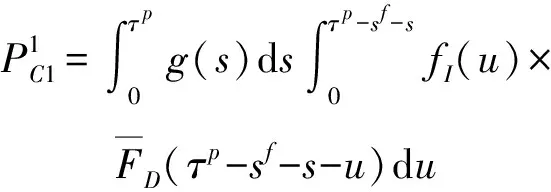
(4)

如果部件在周期內未發生失效，則該情況的轉移概率為

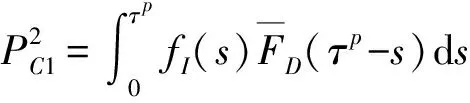
(5)

綜上，1情況的轉移概率為

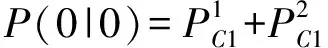
(6)

2)2：初始年齡為，周期結束時需要進行PR，轉移概率為(0|)

當初始年齡為時，部件剩余壽命的概率密度為

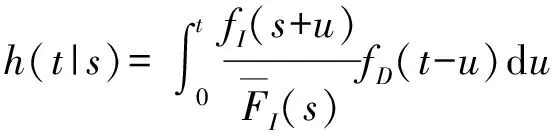
(7)

因此，如果部件在周期內發生失效，則該情況的轉移概率為

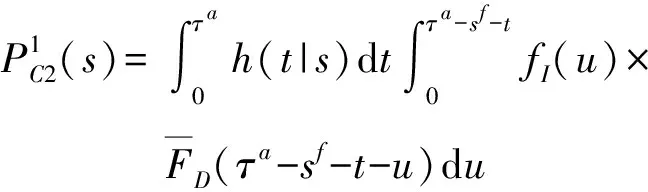
(8)

如果部件在周期內未發生失效，則該情況的轉移概率為

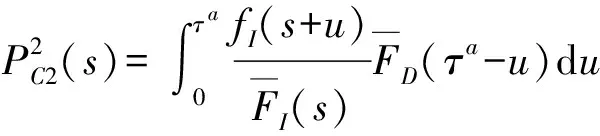
(9)

綜上，2情況的轉移概率為

(10)

3)3：初始年齡為0(更換后)，周期結束時無需進行PR，轉移概率密度(|0)

如果周期內部件發生失效(一次)，則失效時間為--，且故障更換后的部件在剩余周期內一直處于正常態；另一方面，如果未發生失效，則必然要求該部件一直處于正常態，且=。綜上，3情況的轉移概率密度函數為

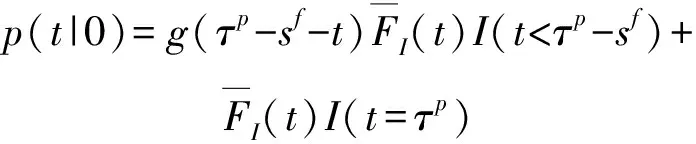
(11)

式中：(·)表示示性函數：如果括號內條件成立則函數值為1；否則為0。(≤-)表示只有≤-時才可能存在失效情況。

4)4：初始年齡為，周期結束時無需進行PR，轉移概率密度(|)

如果周期內部件發生失效(一次)，則失效時間為--，且故障更換后的部件在剩余周期內一直處于正常態；另一方面，如果未發生失效，則必然要求該部件一直處于正常態，且=+。綜上，4情況的轉移概率密度函數為

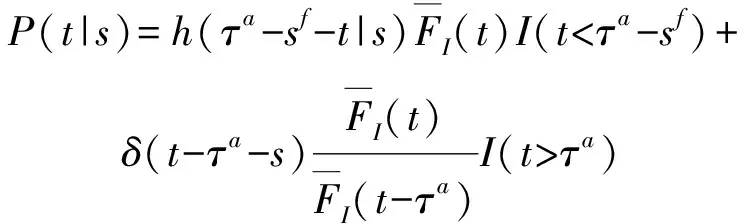
(12)

式中：()為Dirac函數。第二項使用(--)表示只有當=+時才成立。(·|)由(7)式確定。

綜合1～4，可確立穩態狀態概率方程求解檢修后年齡為0的概率和年齡為的概率密度函數()，>0，如(13)式所示：

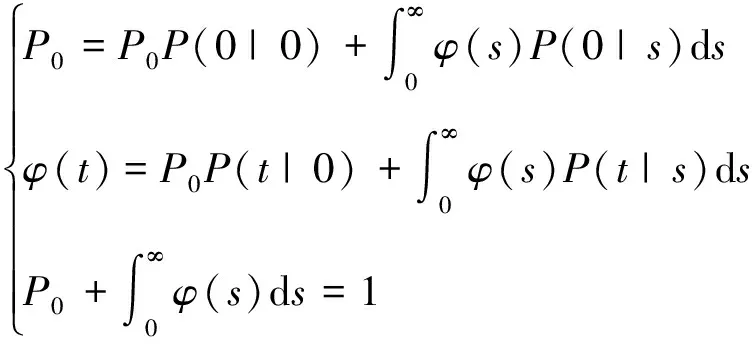
(13)

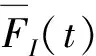
(14)

易知方程組(14)式為(+1)維線性方程組，較易求解。值得注意的是，也表示部件在檢測點進行PR的概率，1-則表示在周期檢測點只進行檢測活動的概率。

為求解部件的平均可用度，需要計算它在檢測周期內發生失效的概率。如果初始年齡為0，則失效概率為

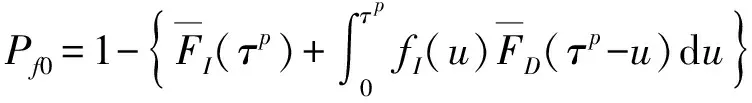
(15)

如果初始年齡為，則失效概率為

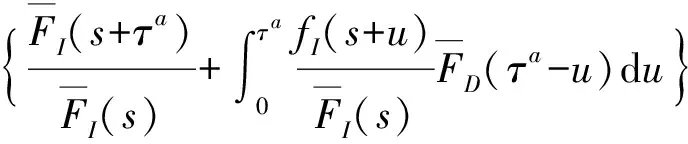
(16)

則缺陷件的平均可用度為

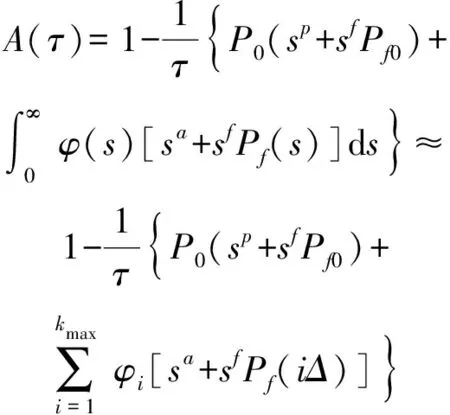
(17)

2.2 系統群組維護優化

飛機系統級維護采用成組維護策略，即各部件的更換檢測周期為其中最短周期(稱為基礎周期)的整數倍，以共享維修固定時間，減少飛機停機時間。系統級成組維護優化在部件級維護策略基礎上進行。

根據(3)式或(17)式，部件∈N∪N的部件級最優更換檢測周期為

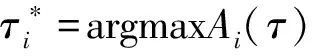
(18)

ki=τ?iτ?c?,Ai(?τ?i/τ?c?」τ?c?)> Ai(?τ?i/τ?c?」τ?c?+τ?c?)τ?iτ?c?+1,其他ì?í????????

(19)

式中：?·」表示向下取整。顯然=1。

在根據(19)式確定各部件周期倍數{,∈N∪N}之后，通過調整基礎周期以確定各部件的調整后維護周期。因此，基礎周期為飛機系統級維護的優化決策變量。

下面計算成組維護下飛機系統的平均可用度。首先注意到所有部件維護周期的最小公倍數即為系統的更新周期，記為×。

當=,=1,2,…,時(稱為第個系統維護點)，計劃進行維護(包括檢測和預更換)的部件集合為C，即

C={|可被整除}

(20)

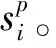
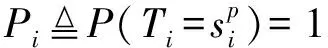
(21)

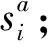
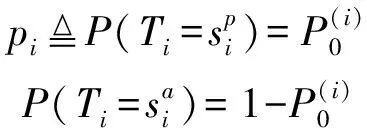
(22)

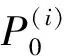
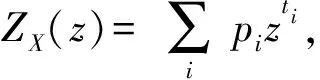
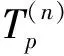
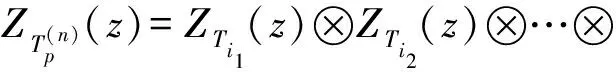
(23)

根據(23)式和變換定義，維護時刻飛機系統平均計劃維護停機時間為

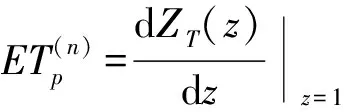
(24)

(25)

綜上，綜合(24)式、(25)式飛機系統在成組維護策略下的平均可用度為

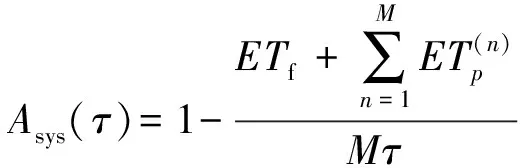
(26)

最優基礎周期可通過最大化系統平均可用度確定，即

=argmax()

(27)

根據(19)式，部件在系統級成組維護策略下的更換檢測的周期為。

3 飛機備件預測仿真

本節在飛機成組維護策略基礎上確定各部件在規劃周期內的備件需求量。各部件在進行PR和CR時均產生備件需求，理論上計算規劃周期內備件需求量的概率分布較為復雜，因此本節給出備件需求量的仿真算法。

設規劃周期為，其中為成組維護策略中的基礎周期。定義|N|×1向量defect表示各缺陷件缺陷發生時間；(|N|+|N|)×1維向量fail和spare分別表示各部件失效發生時間和總備件需求量。備件需求量的仿真流程如圖2所示。仿真算法的核心思路是：

1)以每一個基礎維護周期開始時刻為觀測點，根據各部件仿真失效時間確定在觀測點前一個周期內是否進行CR(更新defect和fail預計值)，直至所有部件的預計(仿真)失效時間均在當前觀測點之后；

2)根據成組策略確定當前觀測點需要進行預防性維護的部件集合C。其中所有壽命件和已出現缺陷的缺陷件均需要PR。對PR件更新defect和fail預計值；

3)每次PR和CR對應部件的備件需求數加1，過程直至觀測點到達為止。

圖2算法可得到一次仿真樣本，重復10次可統計確定各部件所需備件量的統計分布和平均值等。所得備件需求預測結果可根據實際情況制定和優化備件訂購策略，此部分內容不作為本文討論重點。

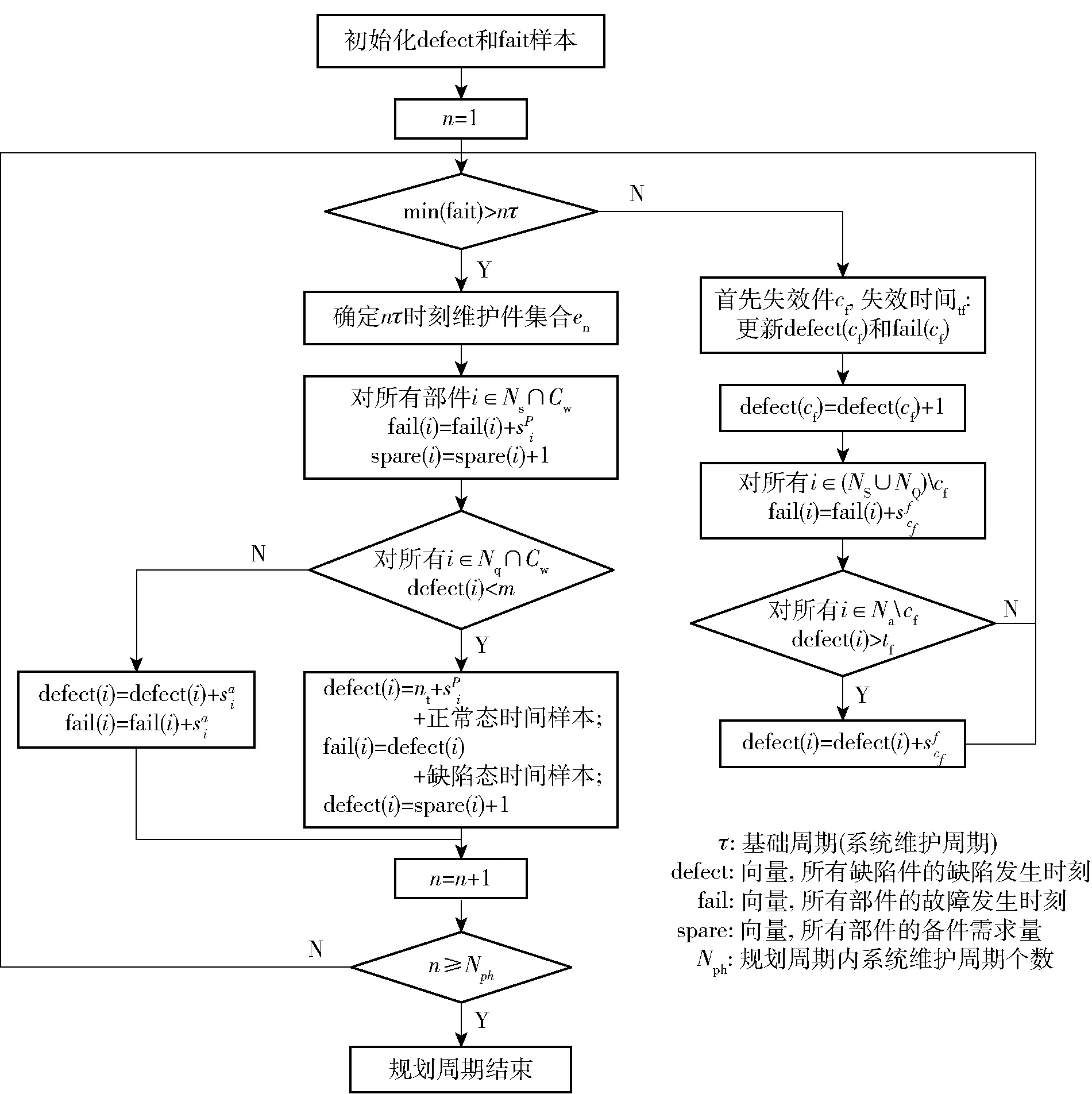
圖2 飛機系統規劃周期內各部件備件需求量仿真流程Fig.2 Simulation flow chart of spare parts demand in the planning horizon of the aircraft system

4 算例

根據第2節和第3節中的飛機維護和備件預測模型，本節給出相應數值算例，并說明所提出的成組維護策略在提高使用可用度方面的效果。

假設飛機檢修計劃共涵蓋10個設備(部件)，其中5個部件屬于壽命件(定期更換)，5個屬于缺陷件(定期檢測)。由于飛機設備多為機電類設備，因此不失一般性考慮威布爾分布用來描述部件的失效時間。威布爾分布的CDF和PDF分別為

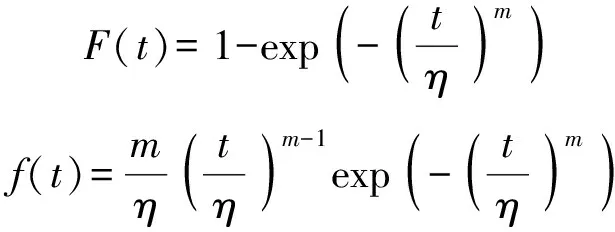
(28)

式中：為尺度參數，反映特征壽命大小；為形狀參數，反映失效機理。特別地，取值大于1，表示失效率遞增，反映機電類產品疲勞、磨損、腐蝕等失效機理。

對所有10個部件進行編號，假設1號～5號表示缺陷件，6號～10號表示壽命件，對應的壽命參數如表1所示。

表1 飛機缺陷件和壽命件壽命參數

假設飛機每次進行維護時所需固定時間=12 h，包括等待、入庫，初步拆卸、人員與設備準備時間、維護結束后測試等，此類時間為系統層時間，不計入部件層維護活動。各部件檢測時間、預防性更換時間，故障更換時間如表2所示。

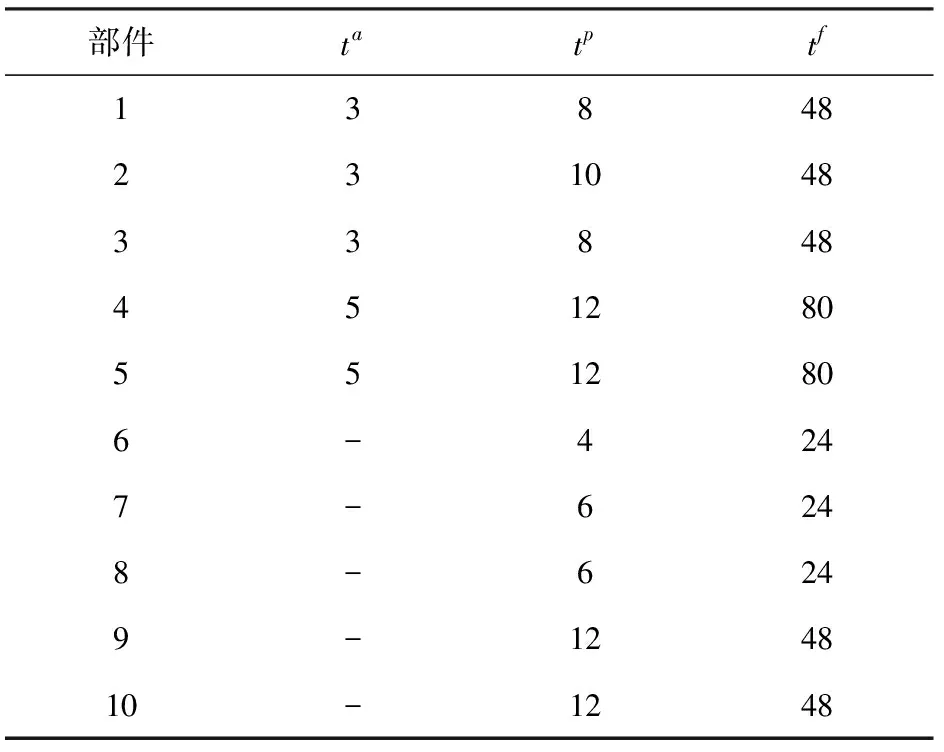
表2 飛機各部件檢測和更換時間

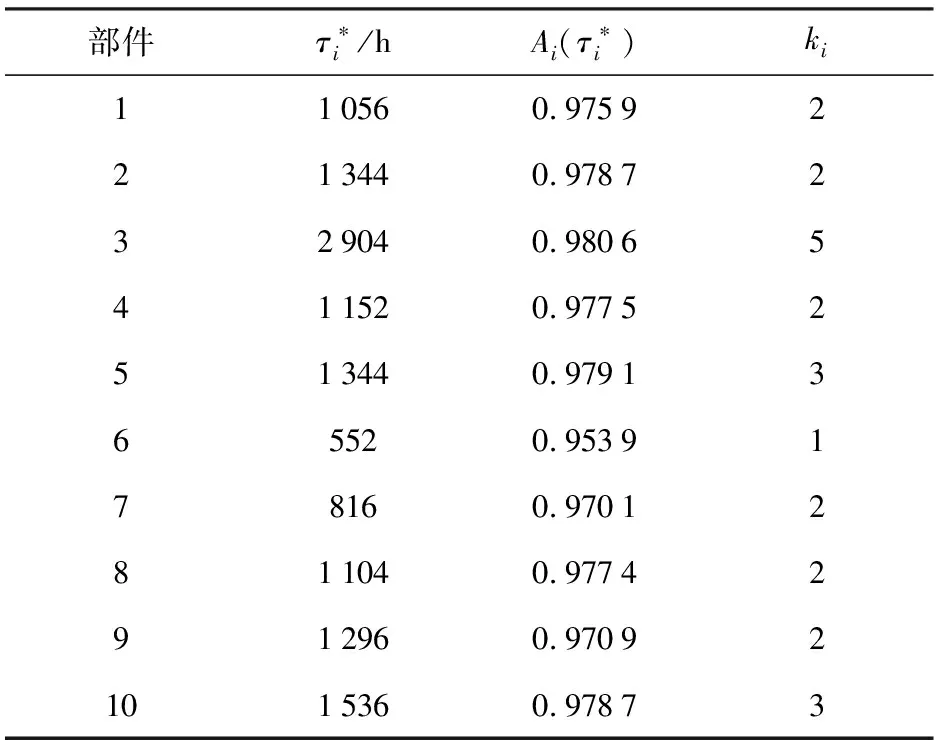
表3 飛機各部件的部件級維護優化參數

(29)

兩種系統可用度計算結果如圖3所示。最優基礎周期為=288 h(12 d)，對應可用度最大(=0900 5)。可以看出，采用成組維護策略后系統可用度提高效果明顯，原因是成組維護可將多個部件維護進行組合，實現多任務并行和共享系統層維護固定時間。

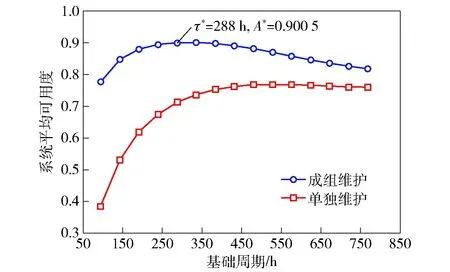
圖3 兩種維護策略下的系統可用度對比Fig.3 Comparison of system availability under the two maintenance strategies

表4給出在最優基礎周期下各部件在系統層級的維護周期(檢測或預防性更換)，并給出了各缺陷件在一個檢測周期內失效不超過1次的概率，以及各壽命件在一個預防性更換周期內失效不超過2次的概率。從表4中可以看出，這些概率值均非常小，驗證了21節為簡化建模所作假設是合理的。

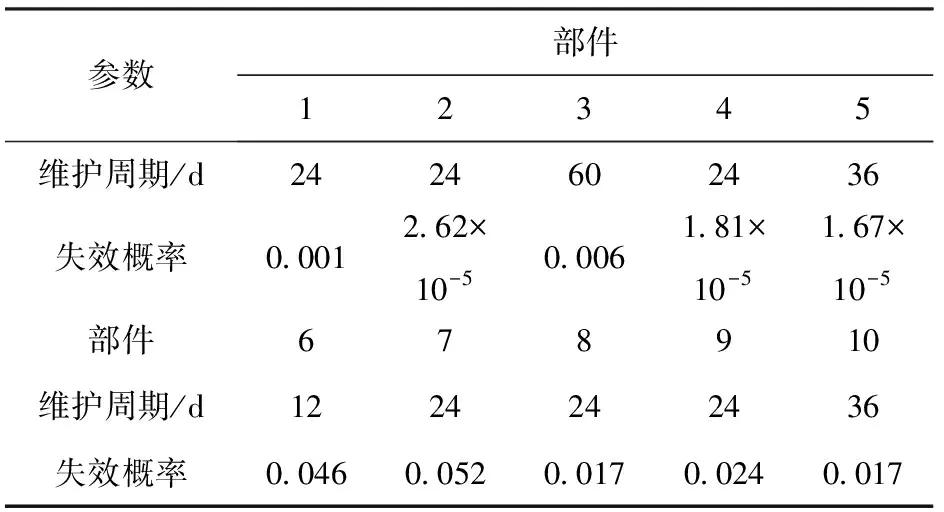
表4 各部件維護周期內失效超過1次的概率

進一步，可以考察系統維護準備時間對系統可用度的影響。

圖4給出了成組維護和單獨維護策略下可用度隨變化曲線圖。

顯然可用度隨增大而減小，此外圖4還表明隨著增大，兩種策略間的差距略有增大，表明成組維護效果提升明顯。此外，一個特別的現象是當減小接近0時，兩種策略效果仍有較大差距，這是因為成組維護除了能共享，更重要的是還能夠使得多預防性維護任務并行進行，較少停機時間。

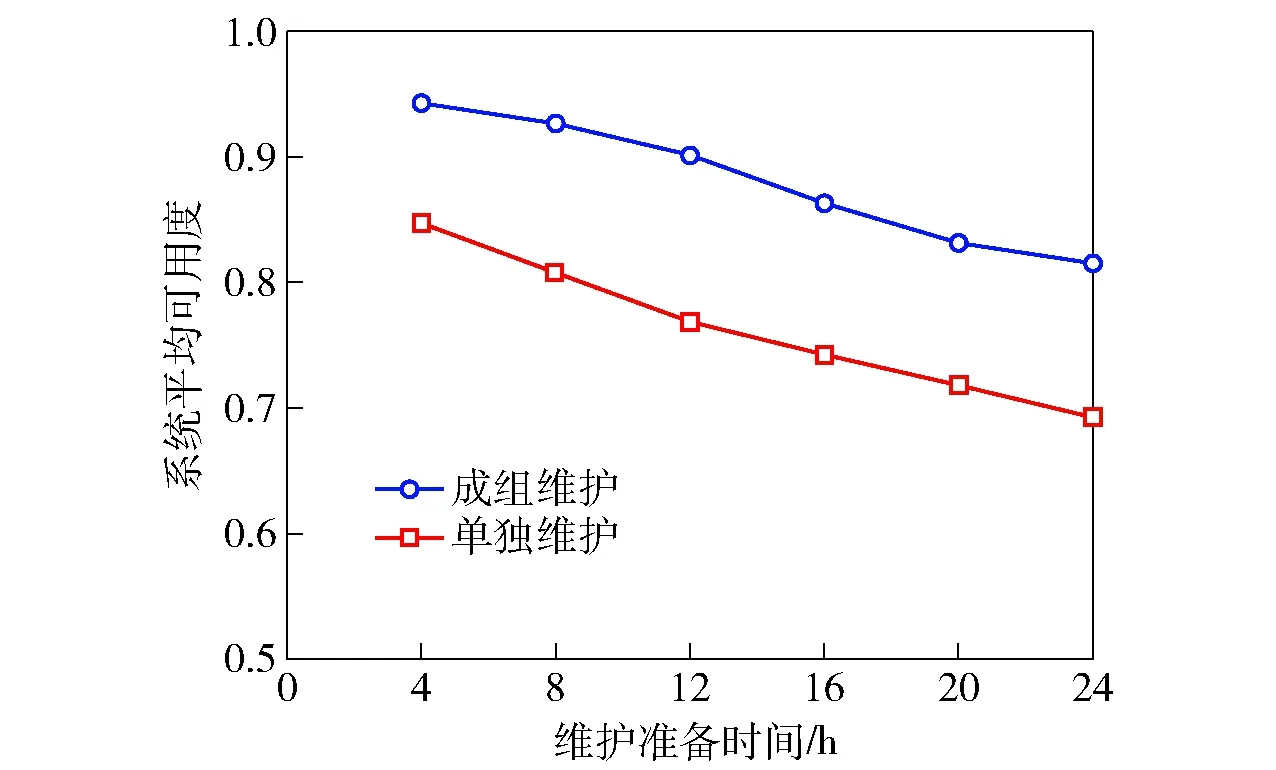
圖4 系統可用度隨維修固定時間ts變化圖Fig.4 Variation of system availability with fixed maintenance time of ts

最后在給定維護策略下，假定規劃周期為1年，根據圖2仿真流程(仿真1 000次)計算各部件在規劃期內的備件需求預測分布，結果如圖5所示；平均備件需求量如表5所示。

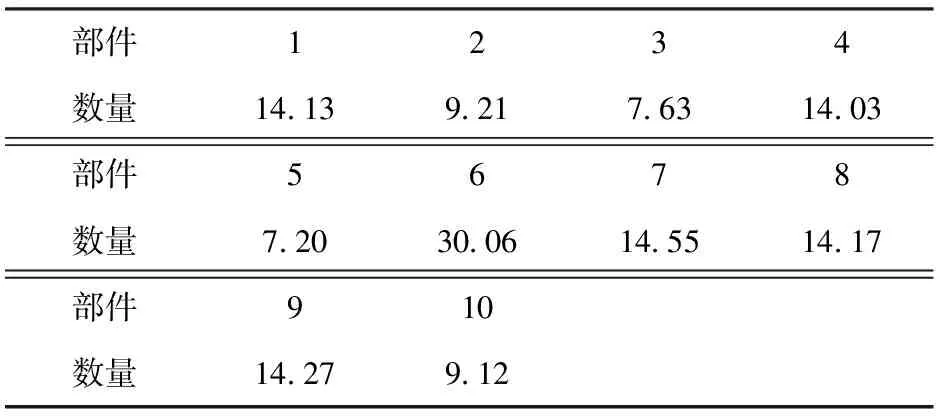
表5 規劃期(1年)內平均備件需求量

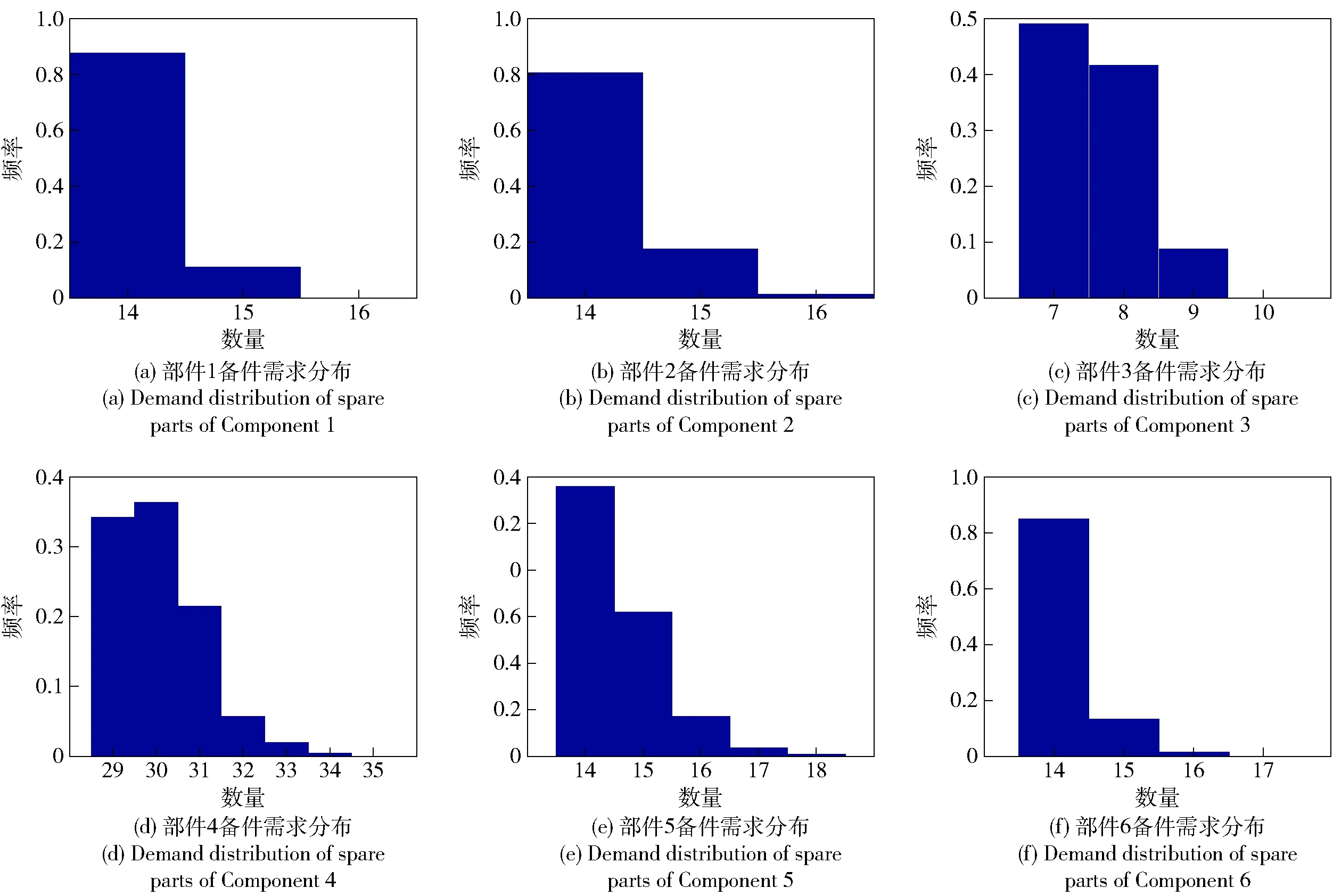
圖5 各部件在規劃周期(1年)內的備件需求量分布Fig.5 Spare parts demand distribution within the planning period (1 year) of each component

5 結論

本文以優化飛機可用度為目標，針對壽命件和缺陷件制定成組維護策略、建立部件可用度和系統可用度模型，最后在優化策略的基礎上實現備件需求預測。該維護策略可組合多部件維護活動，具有優勢：1)多維護任務并行進行；2)共享系統層維護固定時間，從而達到減少飛機維護停機時間、提高使用可用度的目的。優化過程分為兩階段：首先建立各部件可用度模型，進行部件級策略優化；在此基礎上，確定各部件維護周期倍數，建立系統可用度模型，最終優化系統級策略。本文提供的數值算例表明成組維護策略相比于各部件獨立維護對飛機系統可用度提升明顯，備件需求分布仿真預測可對后續備件訂購優化提供基礎。

[1] 涂繼亮, 余洪, 余松, 等. 基于性能保障分析的飛機備件需求預測模型 [J]. 海軍航空工程學院學報, 2019, 34(4): 356-362.

TU J L, YU H, YU S, et al. Aircraft spare parts requirement forecasting model based on performance support analysis[J]. Journal of Naval Aeronautical and Astronautical University, 2019, 34(4): 356-362. (in Chinese)

[2] 王華. 飛機維修控制在成本控制中的應用 [J]. 科技創新與應用, 2017(16): 297.

WANG H. The application of aircraft maintenance in costs control[J]. Technology Innovation and Application, 2017(16): 297. (in Chinese)

[3] 蘇亨鋦. 測試數據下的航空裝備視情維修研究 [J]. 設備維修與管理, 2018(11): 54-55.

SU X J. Condition-based maintenance of aerial equipment given testing data[J]. Plant Maintenance Engineering, 2018(11): 54-55. (in Chinese)

[4] 鄭志霖, 葉曉東. 基于統計分析方法的飛機維修方案優化 [J]. 航空維修與工程, 2020(11): 29-33.

ZHENG Z L, YE X D. Optimization of aircraft maintenance scheme based on statistical analysis method[J]. Aviation Maintenance & Engineering, 2020(11): 29-33. (in Chinese)

[5] LIU J Q. Maintenance model of aircraft structure based on three-stage degradation process [J]. Computers & Industrial Engineering, 2021, 157: 107335.

[6] 楊力, 馬小兵. 維修- 更換串聯系統貯存可用度建模及費用分析 [J]. 兵工學報, 2015, 36(3): 552-558.

YANG L, MA X B. Storage availability modeling and cost analysis for a repair-replacement series system[J]. Acta Armamentarii, 2015,36(3):552-558. (in Chinese)

[7] 祝華遠, 李軍亮, 孫魯青. 武器裝備通用質量特性管理綜述 [J]. 兵工自動化, 2021, 40(2): 13-17.

ZHU H Y, LI J L, SUN L Q. Overview of weapon equipment general quality characteristics management[J]. Ordnance Industry Automation, 2021, 40(2): 13-17. (in Chinese)

[8] 馬小兵, 楊力. 貯存可用度約束下的可修系統壽命評估與優化 [J]. 系統工程與電子技術, 2015, 37(3): 572-576.

MA X B, YANG L. Life evaluation and optimization for a repairable system under the constraints of storage availability[J]. System Engineering and Electronics, 2015, 37(3): 572-576. (in Chinese)

[9] 陳博, 徐常凱, 徐啟豐. 基于DEVS-OODA 模型的作戰飛機備件保障仿真研究 [J]. 物流科技, 2018, 41(11): 129-131.

CHEN B, XU C K, XU Q F. Simulation of spare parts emergency support for carrier-based aircraft based on DEVS-OODA[J]. Logistics Sci-Tech, 2018, 41(11):129-131. (in Chinese)

[10] 陳云翔, 李巖, 蔡忠義, 等. 基于HTCPN的飛機維修保障資源配置方法 [J]. 系統工程與電子技術, 2020, 42(9): 2130-2139.

CHEN Y X, LI Y, CAI Z Y, et al. Allocation method of aircraft maintenance support resources based on HTCPN[J]. Systems Engineering and Electronics, 2020, 42(9): 2130-2139. (in Chinese)

[11] 李巖, 陳云翔, 蔡忠義,等. 戰時軍用飛機維修保障人員數量確定方法 [J/OL]. 火力與指揮控制.http://kns.cnki.net/kcms/detail/14.1138.TJ.20200925.1042.020.html.

LI Y, CHEN Y X, CAI Z Y, et al. Method for determining the quantity of maintenance support personnel of military aircraft in wartime[J/OL]. Fire Control & Command Control, http://kns.cnki.net/kcms/detail/14.1138.TJ.20200925.1042.020.html. (in Chinese)

[12] DE JONGE B, JAKOBSONS E. Optimizing block-based maintenance under random machine usage [J]. European Journal of Operational Research, 2018, 265(2): 703-709.

[13] KE H, YAO K. Block replacement policy with uncertain lifetimes [J]. Reliability Engineering & System Safety, 2016, 148: 119-124.

[14] LAGGOUNE R, CHATEAUNEUF A, AISSANI D. Opportunistic policy for optimal preventive maintenance of a multi-component system in continuous operating units [J]. Computers & Chemical Engineering, 2009, 33(9): 1499-1510.

[15] BERRADE M D, SCARF P A, CAVALCANTE C A V. A study of postponed replacement in a delay time model [J]. Reliability Engineering & System Safety, 2017, 168: 70-79.

[16] VAN OOSTEROM C D, ELWANY A H, CELEBI D, et al. Optimal policies for a delay time model with postponed replacement [J]. European Journal of Operational Research, 2014, 232(1): 186-197.

[17] YANG L, MA X B, ZHAI Q Q, et al. A delay time model for a mission-based system subject to periodic and random inspection and postponed replacement [J]. Reliability Engineering & System Safety, 2016, 150: 96-104.

[18] HUANG W Y, CHENG J S, YANG Y. Rolling bearing fault diagnosis and performance degradation assessment under variable operation conditions based on nuisance attribute projection [J]. Mechanical Systems and Signal Processing, 2019, 114: 165-188.

[19] SHAFIEE M, FINKELSTEIN M. An optimal age-based group maintenance policy for multi-unit degrading systems [J]. Reliability Engineering & System Safety, 2015, 134: 230-238.

[20] KROES M J, WATKINS W A, DELP F. Aircraft maintenance & repair [M]. 7th ed. New York，NY，US: McGraw-Hill, 2013.

[21] ZHANG C X, LI Q, LIU Y K. Optimal replacement policy with minimal repair and preventive maintenance of an aircraft structure subjected to corrosion [J]. Soft Computing, 2020, 24(1): 375-384.

[22] REN H, CHEN X, CHEN Y. Reliability based aircraft maintenance optimization and applications [M]. London，UK: Academic Press, 2017.

[23] LIU B, YEH R H, XIE M, et al. Maintenance scheduling for multi-component systems with hidden failures [J]. Ieee Transactions on Reliability, 2017, 66(4): 1280-1292.

[24] QIU S Q, MING H X G. Reliability evaluation of multi-state series-parallel systems with common bus performance sharing considering transmission loss [J]. Reliability Engineering & System Safety, 2019, 189: 406-415.

[25] WU D, CHI Y Y, PENG R, et al. Reliability of capacitated systems with performance sharing mechanism [J]. Reliability Engineering & System Safety, 2019, 189: 335-344.