橋梁施工纜索吊裝系統地錨單樁數值模擬與分析
肖正恩,周海發,王壽武,朱莎莎
(1.云南云橋建設股份有限公司,云南 昆明 650101;2.昆明理工大學,云南 昆明 650051;)
橋梁施工纜索吊裝系統的樁式地錨施工簡單,效果明顯,但其穩定性易受周圍土體性質影響。樁式地錨在受力時有豎直方向和水平方向運動趨勢,在豎直方向上的受力作用類似于抗拔樁,受上拔荷載的影響,在水平方向上的受水平拉力的影響。目前,國內對于樁式地錨的受力變形計算大多借鑒抗壓樁的理論,且由于群樁效應的存在,在理論驗證時大多采取驗證單樁的方法。隨著計算機程序的快速發展,各種數值模擬軟件被大量開發并投入應用,使得實際工程可以通過模型的形式比較形象地展現在設計者面前。林峰對樁式地錨的設計理論和施工流程做了介紹,說明了樁式地錨在橋梁的纜索吊裝中的適用性和優越性;姜成潼利用理論計算和數值模擬方法對某邊坡工程采取的樁錨-框錨支護結構的受力機理進行研究,將得到的樁頂水平位移值與一般支護結構對比,證明了樁錨-框錨支護結構能夠更好地平衡剩余邊坡滑力。本文在前人研究的基礎之上,基于實際工程背景,運用理論計算和數值模擬相結合的方法對某斜拉橋施工纜索吊裝系統地錨施工方案中的單樁進行穩定性進行驗證,并分別改變單樁的樁長、樁徑和拉索角度,分析單樁因素改變對樁身位移的影響。
1 工程背景
1.1 工程概況
斜拉橋項目位于云南省某高速公路上,全程1330米,主橋為雙塔三跨鋼箱斜拉橋。施工纜索吊裝系統布置如圖1所示。根據鉆孔勘探資料可知土層大致分為三種,根據粒徑和含量多少可知研究點土層巖性多屬于漂石粒組和卵石粒組的巨粒土,還有部分粗粒組即細砂,因此認為力學性質主要按照碎石土分類,具體分層參數見表1。
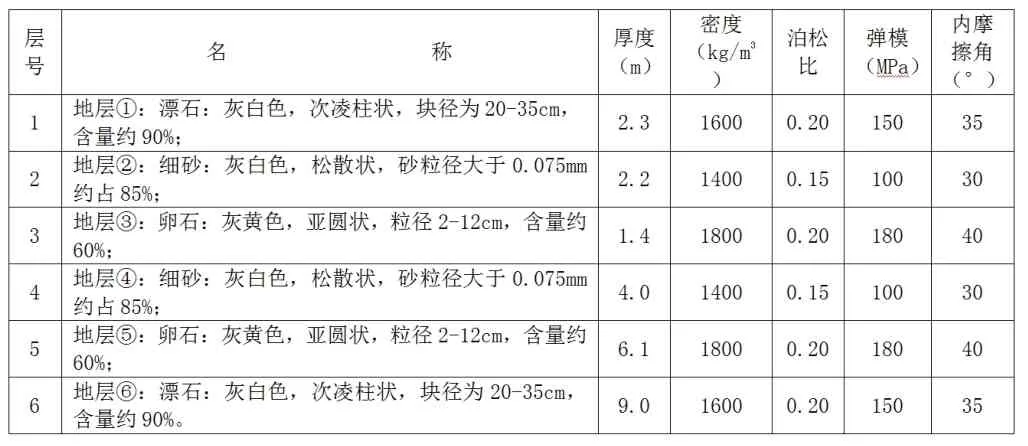
表1 土層參數
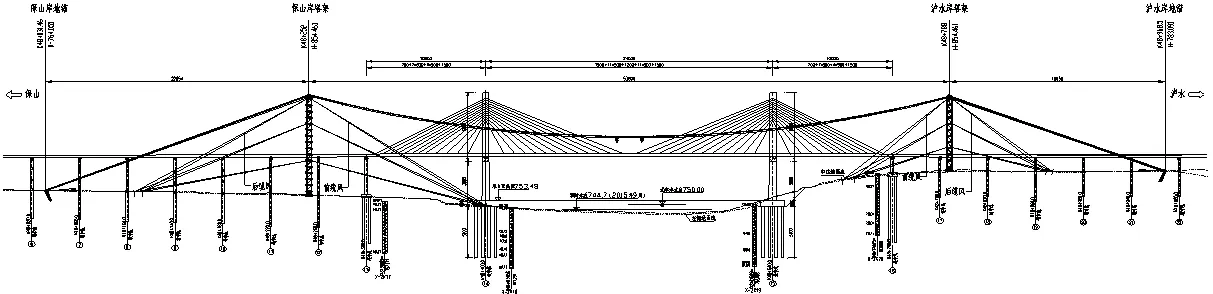
圖1 纜索吊裝系統布置圖
1.2 橋梁施工纜索吊裝系統地錨施工方案
橋梁施工纜索吊裝系統地錨采用樁式地錨,樁長16m,樁徑2.0m,共9 根,梅花型雙排樁布置,采用C30 鋼筋混凝土鉆孔灌注樁。群樁樁頂設置C30 混凝土承臺,承臺尺寸25×10×2m。布置如圖2所示。
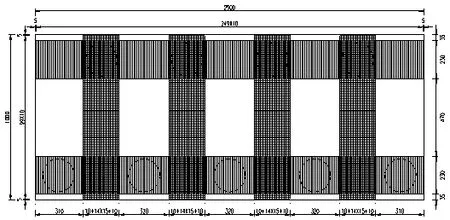
圖2 樁式地錨布置圖(cm)
2 單樁數值模擬分析
2.1 基本假定和模型
基本假定和模型如下:①忽略水流對土體開挖的影響,不考慮土體流失對樁土體產生的影響;②巖土體為均勻地質;③群樁樁頂與承臺剛性連接;④假設9 根樁平均受拉;⑤土體模型采取圓柱形隧道外圍漸變網格(radcylinder),本構關系為莫爾庫倫;樁體建模采用柱體網格(cylinder),本構關系為彈性。樁土之間的相互作用采取接觸面(interface)來模擬受力。以樁心為原點在FLAC 3D 中建立以x、y、z 三軸為方向的坐標系,x 軸向右為正,z 軸向下為負,按照地層厚度建立三維模型。有限差分計算域為8m×8m×27m。
2.2 模擬結果分析
圖3是單樁受極限拉力作用下在水平方向產生的樁土位移云圖。圖4是隱藏土層,只顯示單樁水平位移的模擬圖。從圖中可知受極限拉力后,單樁在靠近樁頂附近的區域產生較大的水平位移值,最大數值為5.05mm,在接近樁底附近的范圍,水平位移值較小,平均水平位移值為2.8mm。隨著樁深的增加,水平位移值逐漸減小,可知來自上部的荷載從樁頂到樁底再到土層達到了較好的傳遞受力效果。根據規范中允許敏感性樁身的最大水平位移小于或等于6mm 時樁身不開裂,說明模擬結果相對安全。
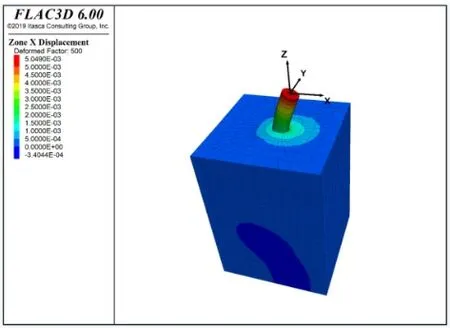
圖3 放大樁土水平位移效果圖
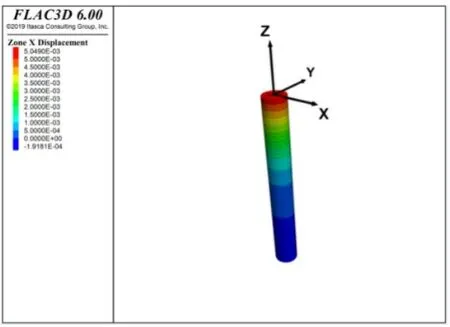
圖4 單樁模擬水平位移云圖
3 水平位移理論計算與分析
已知最大拉力合力T=11048.285KN,則水平推力,豎直上拔力。地基比例系數m 取常數為20000KN/m4 ,則樁身計算寬度和變形系數為:
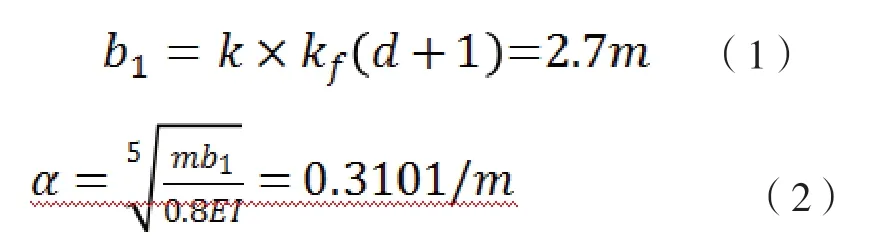
式中:k 為基礎形狀的換算系數,kf 為平面工作條件的系數,EI為樁身抗彎剛度,由于α×h=4.96>2.5,故按照彈性樁計算。
將水平拉力平均分配給9 根樁基,樁頭彎矩M是水平拉力的0.3 倍,Ax 表示單位水平力產生的樁頂水平位移,B表示單位彎矩產生的樁頂水平位移,根據彈性樁規定查表可得數值,最終得到樁頂x軸向位移:
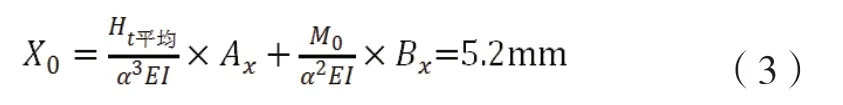
數值模擬得到的最大水平位移值為5.05mm,而理論計算結果為5.2mm,都在規范的安全范圍內且兩者的誤差僅約為2.88%。存在的誤差是因為數值模擬在程序計算中將更多的地質參數代入了計算,所以使得計算結果偏小。
4 不同工況下樁身最大水平位移分析
為研究單樁在受極限荷載作用下樁長、樁徑和拉力角度分別改變對單樁水平位移產生的影響,將模擬不同工況下單樁樁身位移并對這些具體的數值進行分析對比。分三種工況:①樁徑、拉力角度不變,改變樁長;②樁長、拉力角度不變,改變樁徑;③樁長、樁徑不變,改變拉力角度。
在FLAC 3D 中監測不同工況下樁身受拉產生的最大水平位移,三種工況的監測數據如圖5、圖6、圖7所示。

圖5 不同樁長最大水平位移值監測圖
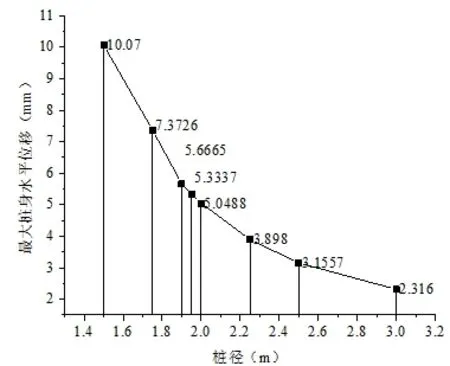
圖6 不同樁徑最大水平位移值監測圖
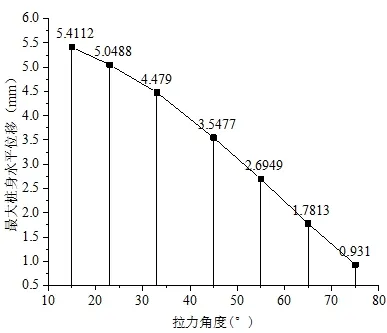
圖7 不同拉力角度最大水平位移值監測圖
(1)從圖5可知,在改變樁長,不改變其他條件的情況下,樁長以12m 為初始值,每隔1m 遞增,直到19m 結束,發現樁身最大水平位移值隨樁長增加而減小且均小于6mm 并在5mm 左右上下浮動,樁長在12~19m 之間,樁身未產生開裂現象,單樁處于較穩定狀態。
(2)在改變樁徑,不改變其他條件的前提下,樁徑以1.5m 為起始值,按照0.05m、0.15m、0.25m 或者0.5m不定值增加,以3m 為結束值,從圖6可知隨著樁徑逐漸增大,最大樁身水平位移值逐漸減小,兩者呈負相關關系。樁徑為1.5m 和1.75m 時,最大樁身水平位移值超過了6mm,按規范判斷,該單樁有可能會發生樁身開裂現象,此時的兩個樁徑值不能被作為樁徑設計值,樁徑值在1.90~3.0m 之間,最大水平位移值在規定的安全區間,可以被作為設計值選取使用,考慮到施工成本的問題,盡可能在保證安全的前提下選擇較小樁徑值。
(3)從圖7可知,在改變拉力與單樁傾角,不改變其他條件時,拉力角度與最大樁身水平位移的關系近似成直線型下降趨勢,可見適當增大拉力角度能夠有效較小樁身的水平位移,但是限于施工現場拉索布置要求以及其他結構的布置,拉力角度不能夠自由變化,所以可在限制條件下盡量使拉力角度大一點。
5 結論
(1)通過對比數值模擬與理論計算的結果可知:樁長16m,樁徑2.0m,拉力角度為23°時的單樁模擬最大水平位移約為5.05mm,計算最大水平位移約為5.2mm,均在6mm 之內,單樁樁身不會開裂,兩種方法的誤差也在合理范圍,該橋所采用的纜索吊裝系統地錨方案可行;
(2)通過單方面地去增大樁長、樁徑或拉力角度都可以在一定程度上減小單樁樁身的水平位移,以達到使樁身更加穩定的目的,考慮到施工成本和其他因素的影響,要有效選取較為合適的設計參數;
(3)通過對比樁長、樁徑和拉力角度分別改變后的樁身水平位移可知樁徑改變對位移的影響較大。

