帶有初態偏差的離散時滯系統控制策略

李國軍,陳東杰,董齊芬,王亢

(1.浙江警察學院公共基礎部,浙江 杭州 310053;2.浙江警察學院計算機與信息安全系,浙江 杭州 310053)

1 引言

迭代學習控制(Iterative learning control,簡稱ILC)適用于在有限區間作重復操作的被控系統,通過反復試驗不斷調整輸入信息來改進輸出效果,以便跟蹤上期望軌跡[1-2].通過足夠多次重復后的ILC具有良好的跟蹤性能,所以常被應用于機器人控制,產品流水線控制,間歇過程控制以及電路穩定性控制等場合.傳統的ILC在應用時,要求每次的初始定位誤差必須等于零或者某個固定值,但這在實際中基本不可能做到,所以說初值問題是迭代學習控制的基本問題之一.因此,研究任意初值條件下的迭代學習控制不僅有必要而且十分有意義.

對于連續系統而言,關于初值研究的文獻較多.文獻[3]首次引入邊界層的概念,并讓邊界層隨著隨著時間單調收斂至零,由于控制誤差受邊界層限定,所以相應的控制誤差也漸近收斂至零,但由于邊界層只能在時間趨向無窮時才收斂至零,所以這種方法達不到完全跟蹤.文獻[4-6]利用吸引子方法達到了實際完全跟蹤.文獻[7-8]采用誤差跟蹤的方法達到了一致性跟蹤,但這種方法在每次迭代時都需要事先重新設定的新的期望軌跡.對于高階可參數化非線性系統,在控制增益已知的情形下,文獻[9]在指定區間達到了精確跟蹤.對于帶有時變迭代參數的不確定系統,文獻[10]利用內模控制方法設計參數學習律,確保系統收斂.在壓縮映射方法研究過程中,對于具有高相對階的系統,文獻[11]提出了一種修正方法,在完成對初態誤差的修正以后,能夠確保系統達到完全跟蹤.對帶有固定初態誤差的高階多智能體系統,文獻[12]用Step-by-step策略逐個修正各個狀態偏差并最終達到了一致性跟蹤.針對非線性連續系統,文獻[13]提出了一種針對任意初態的修正方法,但這種方法不能完全修正初始誤差,而且只適用于一階系統.

對于離散系統而言,近年來研究的學者不多,得到的有益結論并不豐富.對于固定初態情形,文獻[14]借助線性矩陣不等式求解控制器增益,并通過反饋輔助控制方法達到了漸近跟蹤.對于高相對階線性離散系統,文獻[15]達到了漸近跟蹤.而文獻[16-17]針對帶有固定初態的高相對階非線性離散系統,在控制時引入初始修正行為,實現了在指定區間上的一致性跟蹤.文獻[18]提出了一種針對任意初態和時變軌跡的離散自適應ILC方法,能夠確保系統沿著迭代軸漸近收斂,沿著時間軸在指定區間內逐點收斂.文獻[19]對文獻[18]進行了評論,指出了文中的瑕疵.文獻[20]針對非參數化非線性不確定離散系統,得到了類似于文獻[18]的結論.對于控制方向未知的非線性離散系統,針對任意初態情形,文獻[21]中提出的控制策略能夠使系統沿時間軸漸近收斂.

本文提出了一種基于壓縮映射的迭代學習算法,該算法在任意初態下,能夠確保離散時不變時滯系統在指定區間上達到逐點跟蹤,最后通過三個例子驗證了該方法的有效性.

2 問題闡述及控制器設計

考慮下述線性定常時滯系統

其中,t=0,1,2,···,N;k=1,2,···表示迭代次數;d(為正整數且d＜N-1)是時滯參數;xk(t)∈Rn,yk(t)∈Rr,uk(t)∈Rm(相應可以簡寫為xk,uk,yk)分別表示第k次迭代的系統狀態,控制輸入和輸出向量.A,B,C是合適維數的系統參數矩陣,并且B右可逆.

設yr(t)(簡寫為yr)是給定的期望軌跡,設xr(t)(相應簡寫為xr)是給定的期望狀態,ek(t)=yr-yk表示第k次輸出誤差.

假設2.1初始狀態xk(0)隨機,狀態xk(t)可測,并且xk(-d)=0,···,xk(-1)=0.

為了使得系統(1)能夠在指定時間內跟蹤上目標軌跡,提出帶有初始狀態誤差修正功能的控制律.

3 收斂性分析

這一節著重分析系統(1)在應用控制律(2)以后的收斂性.本節中定義‖·‖是向量或矩陣的某種范數,對于上節中提出的控制律(2),有下面的定理.

定理3.1如果初始狀態是任意有限值,并且存在一個矩陣Γ滿足

那么控制律(2)能夠讓系統(1)在區間[1,N]上達到逐點跟蹤.

證明為了方便書寫,記

對于系統(1),當t∈[0,N-1]時,應用控制律(2)并根據假設2.1可得

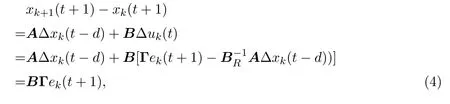
在上式兩端同時乘以矩陣C,可得

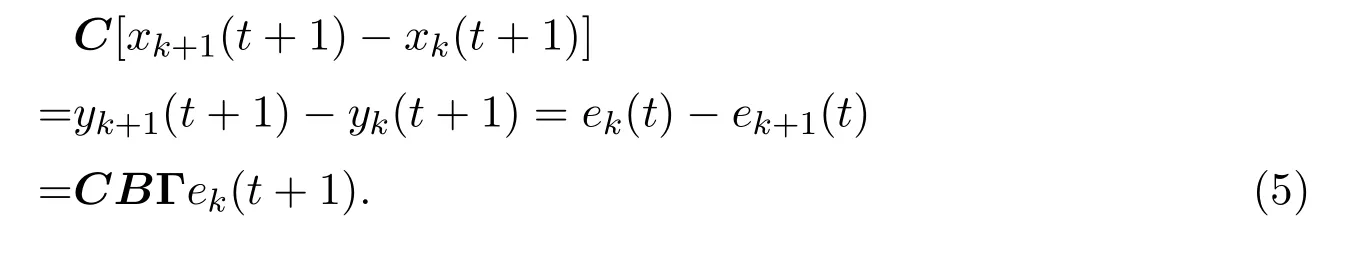
所以有

因此當t∈[0,N-1]并且‖I-CBΓ‖≤1時有

也就是說,在[1,N]上‖ek+1(t)‖逐點收斂于0.

注2.1從上面的證明可知,該算法所決定的系統收斂點與系統的時滯參數d的大小無關.

根據上面的證明可知,對于下面的復雜離散時滯系統

其中,d1,···,dj(1≤di≤N-2,1≤i≤j)是時滯參數,A,A1,···,Aj是合適維數的矩陣,如果該系統迭代初態任意并且矩陣B右可逆,則可以采用下面的控制律使其達到完全跟蹤.

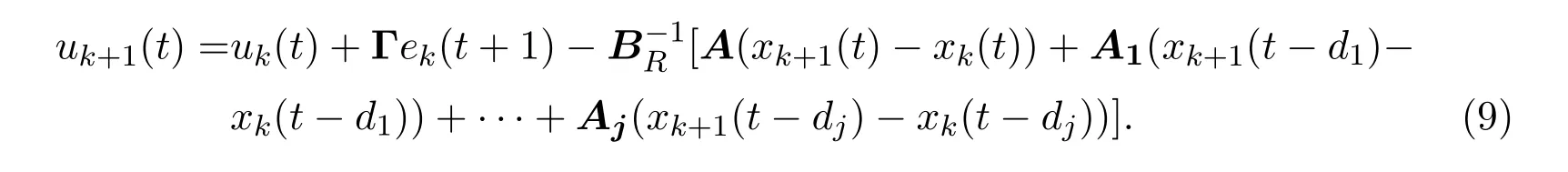
定理3.2如果系統只具有下面的模型

其中,V1(t)是迭代時的固定性擾動,Vk(t)是第k次迭代時的隨機性擾動,若

此時應用控制律(2),該系統依然能夠穩定.

證明對于系統(10),當t∈[0,N-1]時,應用控制律(2)可得

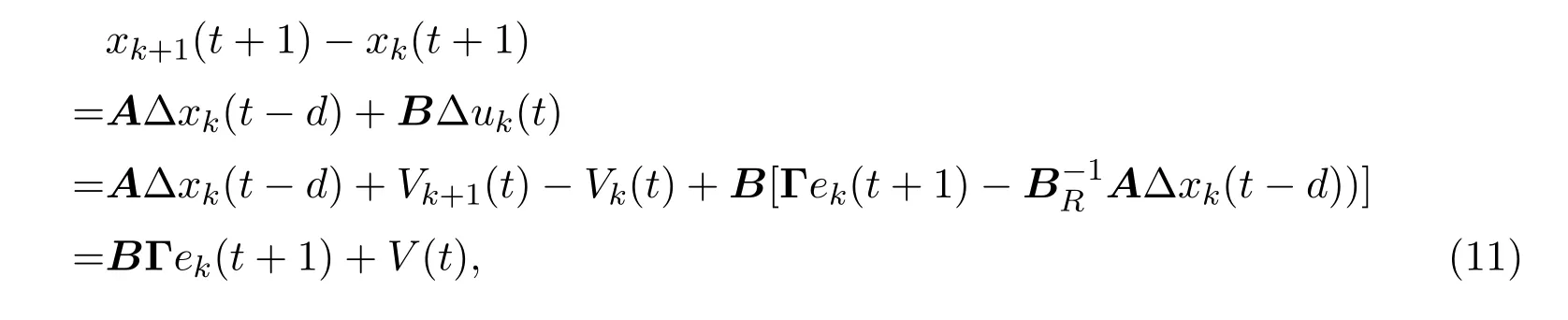
其中,V(t)=Vk+1(t)-Vk(t)是前后兩次隨機性擾動的疊加,從統計意義上來講V(t)依然隨機,只是該擾動的期望和方差與Vk(t)不同而已.

化簡(11)式有

記

當t∈[0,N-1]并且‖I-CBΓ‖≤1時有

因此,在[0,N-1]上‖ek+1(t+1)‖有界.也就是說,在[1,N]上‖ek(t)‖有界,即系統(10)在該區間上穩定.

4 數值仿真

本節將通過三個例子來驗證本文算法的有效性,在仿真過程中,例4.1和例4.2的系統采用時間Ts=0.005秒.

例4.1考慮下面的時滯系統

該系統的作業區間為[0,400].

系統運行之前具有隨機性較大的初始狀態xk(0)=25*rand(rand產生0到1之間的隨機數值),控制律(2)中的控制增益Γ=0.89,仿真中迭代次數為15次.系統的跟蹤軌跡采用文獻[12]中的期望軌跡

從圖1放大圖中的可知,控制律(2)在t=1*Ts時完成狀態修正,完全跟蹤上期望軌跡.在圖2中,誤差統計是從點t=1*Ts開始的,從圖中可以看出,只需要迭代4次就基本能完成跟蹤.從圖3中可以看出,在點t=1*Ts處,控制量uk(t)并沒有收斂,而是在t=5*Ts處才開始收斂(仿真和實際情形相差一個單位采樣時間,因為MATLAB下標從1開始),這是由于時滯因子所致.

圖1 實際軌跡yk(t)和期望軌跡yr(t)

圖2 各次迭代實際跟蹤誤差‖ek(t)‖2

圖3 相應的控制量uk(t)

例4.2考慮下面的復雜時滯系統

該系統的作業區間為[0,200].

系統運行之前初始狀態為

控制律(2)中的控制增益

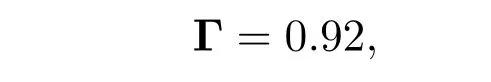
仿真中迭代次數為15次.系統的跟蹤軌跡為

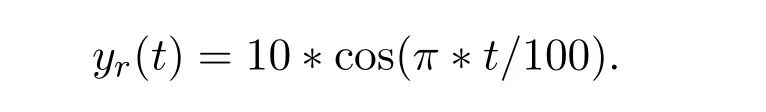
具體仿真結果見圖4-圖6.

圖4 實際軌跡yk(t)和期望軌跡yr(t)

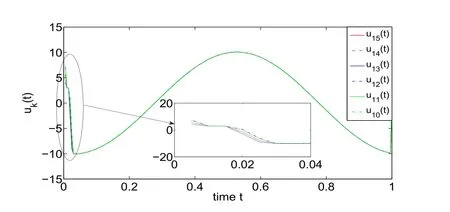
圖6 相應的控制量uk(t)

從圖4中可以看出,系統收斂的時間點和所有的時滯因子都無關,但控制量的收斂時間點和時滯因子有關.本例中最大時滯因子d2=4,所以系統在t=1*Ts時完成狀態誤差修正并跟蹤上期望軌跡,而控制量在t=5*Ts處收斂.從圖6中可以看出,控制量收斂的時間點只和最大的時滯參數有關,與其它時滯參數無關.在圖5中,誤差統計也是從點t=1*Ts開始.

圖5 各次迭代實際跟蹤誤差‖ek(t)‖2

例4.3考慮類似于文獻[13]中的時滯系統

其中,系統運行之前初始狀態為

控制律(2)中的控制增益取值如下:

系統的跟蹤軌跡如下:

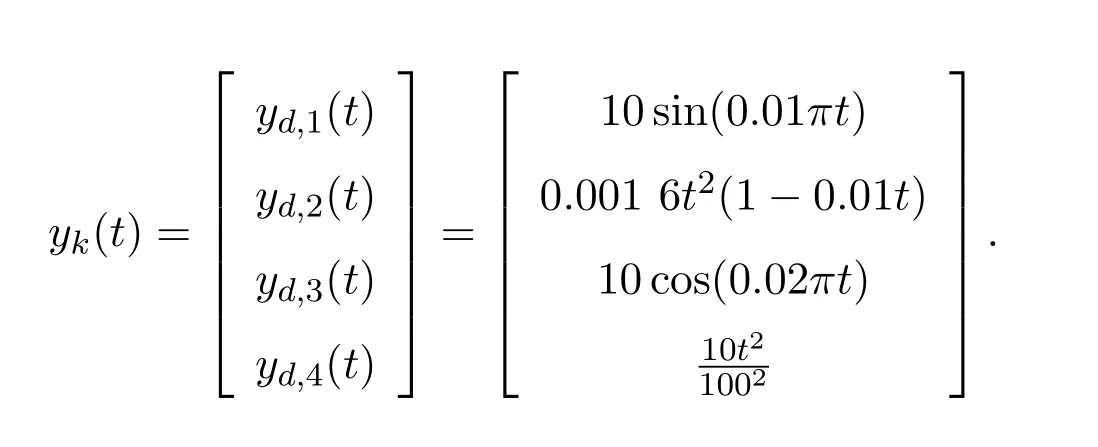
同樣引用該文獻中的指標來表征迭代學習的控制精度:

仿真中迭代次數為15次,圖7和圖9是第15次迭代時的結果.

圖7 期望軌跡yr(t)和實際軌跡yk(t)

圖9 相應的控制量uk(t)

從圖7的放大圖中可以看出,系統沒有達到逐點完全跟蹤,但通過圖8可知,系統在控制率(2)的作用下能夠穩定.

圖8 各次迭代實際跟蹤誤差EE(i)

上面的仿真驗證了本文所提算法對于任意初態下的線性離散時滯系統而言,不管系統是否存在隨機性擾動,系統都能夠穩定.

5 結論

本文討論了線性離散時不變時滯系統存在任意初態誤差的迭代學習控制問題,借助壓縮映射手段,提出了一種帶有修正項的控制策略.在控制過程中,控制算法可以快速修正初態誤差.如果系統沒有隨機性擾動,當修正好狀態誤差后,系統能夠達到無誤差跟蹤;如果系統有隨機性擾動,則誤差位于某個范圍內,而且本文也從理論和實踐兩方面驗證了此算法的有效性.對于系統信息不能精確已知的任意初態偏差情形,目前仍無有效方案,后續本人將從事該方面的研究.