項重寫系統和自由幺半群

林沐辰,朱志成,張毅

(1.南京信息工程大學數學與統計學院,江蘇 南京 210044;2.蘭州大學數學與統計學院,甘肅 蘭州 730000)

1 引言

抽象重寫系統是由文獻[1]首次提出的.文獻[2-4]將抽象重寫系統的對象變成了一些項,稱之為項重寫系統,并考慮了它的性質和廣泛的應用,例如軟件工程,計算機代數,Gr¨obner-Shirshov基礎[5-10],Boolean理論[12-14]和群理論[11].換言之,項重寫系統可以成功地應用于計算機科學、理論計算機科學和數學.

項重寫系統是由一組等式定義的項上的等價類的重寫組成.研究項重寫系統可能面臨的主要問題之一是對具有匯合或終止等基本性質的重寫系統類的刻畫.終止的性質保證了任意項在重寫法則之下都可以終止于一個規范型.此外,如果項重寫系統是匯合的,那么規范型是唯一的.因此,無論重寫法則使用的是哪一種序關系,一個既終止又匯合的項重寫系統保證了它具有唯一規范型的特性,參見文獻[15-18].這些論文對終止和匯合及其相關性質進行了全面研究.終止性和匯合性這兩個性質是極其重要的,本文將基于自由幺半群上的重寫系統對它們進行廣泛研究.

項重寫也可以在Herbrand-G¨odel可計算性中找到.后來,項重寫系統的概念以其目前的形式被提出,并被用于實現規格分析、可計算性理論、字問題和定理證明.隨著里程碑論文中完成方法的出現,文獻[18]為這個領域帶來了新的生機.Knuth-Bendix程序操作重寫系統,這個十分關鍵.這些系統被用來簡化字問題,試圖解決特定的有限群或有限呈現的幺半群的字問題.

終止與匯合問題在重寫系統的研究中起著不可或缺的作用.研究這些問題的一種方法是將注意力限制在簡單類型的代數結構上,如幺半群,這已經被非常成功地運用在文獻[19-21]中.另外,要強調一下,在過去的幾十年里,人們對半群和幺半群上的重寫系統進行了深入的研究.文獻[22]研究了中國幺半群,證明了中國幺半群具有收斂的重寫系統.對于自由幺半群A*中的每一個元素,都有一個算法來求其規范型.因此,中國幺半群的字問題是可解的.給定一個具有有限多左右理想的正則半群,如果每個極大子群都能用一個有限的完備重寫系統表示,那么該半群也是如此.這一結果由Gray和文獻[23]證明.文獻[24]利用楊表計數的組合性質,構造了相應的Plactic幺半群的有限完備重寫系統.

本文沿著這條線,利用重寫系統的理論,研究了收斂重寫系統與自由幺半群的商截面的關系.作為應用,分別得到了由三個元素生成的Plactic幺半群和中國幺半群的商截面.

論文的結構安排如下.在第2章中,首先回顧了項重寫系統的一些基本定義和符號.接下來,研究了專門用于自由幺半群上的項重寫系統的新結果,得到了所使用的重寫系統的一些基本結果.特別地,應用重寫系統的方法給出了一個統一的方法來研究收斂重寫系統和自由幺半群商截面之間的關系.第3章分別研究了由3個元素生成的Plactic幺半群(定理4.1)和中國幺半群(定理4.2)的商截面.

2 自由幺半群上的項重寫系統

本節首先介紹一些基于自由幺半群的項重寫系統的一些符號和結果[25-26].現在,把項重寫系統與集合A生成的自由幺半群A*上的一個二元關系聯系起來.

定義2.1[27]設A是集合,A+是字母表A中所有限非空字a1a2···am的集合.A+上的一個二元運算定義為

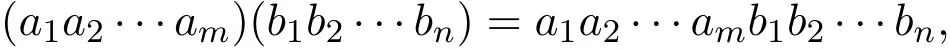
其中m,n∈N.關于這個二元運算,稱A+為A上的自由半群.若在A+中添加單位1(作為空字),則得到A上的自由幺半群,記為A*.

定義2.2設A是集合,S?A*×A*,≤是A*上的線性序.

(a)定義

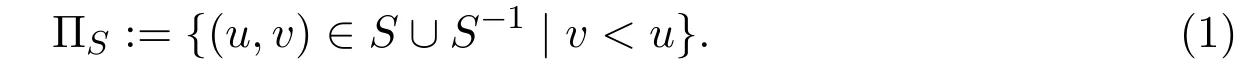
稱系統(A*,ΠS)為與S有關的A*上的項重寫系統.稱ΠS中的元素(u,v)為ΠS的一個重寫法則,記為u→v.

(b)稱f∈A*一步重寫到g∈A*,記為或者更詳細地若存在a,b∈A*和u→v∈S,使得f=aub且g=avb.

(c)稱f∈A*關于ΠS n步(n≥1)重寫到g∈A*,記為若存在f0,f1,···,fn∈A*,使得fi/=fi+1,i=0,···,n-1且

若存在g∈V,n≥1,使得則稱f∈V為可約的.否則稱f為不可約的或者在規范型中.

(d)記二元關系的自反傳遞閉包關系→ΠS(作為A*上的一個二元關系)為若則稱f關于ΠS重寫為g,并稱f是g的前任.記P(g)為g的所有前任的全部集合.因此g∈P(g).

(e)稱f和g是匯合的,記為若存在h∈A*,使得則

定義2.3設A是集合,S?A*×A*,≤是A*上的線性序.稱項重寫系統(A*,ΠS)是

(c)收斂或者完備的,如果它既是終止的又是匯合的.

關于重寫系統的一個眾所周知的結果是Newman′s引理[25].

引理2.1(Newman)終止項重寫系統是匯合的當且僅當它是局部匯合的.

這里需要文獻[28]中的以下定義和引理.

定義2.4[28]稱A*上線性序≤為

(a)可容許的,如果對于任意u,v,x,y∈A*,u≤v可得xuy≤xvy.

(b)良構造的,如果不存在無限形式的鏈x0＞x1＞x2＞···,其中x0,x1,···∈A*.在這種情況下,稱≤為可容許的.

容許良序在重寫系統中起著重要作用,見下面引理.

引理2.2[28]設A是集合,S?A*×A*,≤是A*上的線性序.則下面兩條陳述是等價的:

(a)項重寫系統(A*,ΠS)是終止的;

(b)線性序≤是A*上的一個容許良序.

3 收斂的項重寫系統和截面

本節將刻畫自由幺半群A*上的收斂項重寫系統和A*的商截面之間的關系.

對于一個二元關系S?A*×A*,記〈S〉為S生成的同余.每個同余〈S〉都有一個相應的商結構A*/〈S〉,它是由該關系的同余類組成.

定義3.1設A是集合,S?A*×A*.若對于〈S〉的每一個同余類A,恰好存在唯一的元素w∈W使得w∈A,則稱A*的子集W為A*/〈S〉的截面.

定義3.2設U是半群且U1是具有鄰接單位的半群.設S是U上二元關系.若c,d∈U使得c=xay,且d=xby,對于U1中一些元素x,y,其中(a,b)或(b,a)也屬于S,則可以說c通過一個基本S-傳遞與d相連.

這里需要下列引理.

引理3.1[27]設S是半群U上的關系,并且a,b∈U.則(a,b)∈〈S〉當且僅當a=b或者存在一個基本S-傳遞序列a=z1-z2-···-zn=b,n≥1,連結a到b,其中〈S〉是由S生成的同余.

引理3.2設A是集合,S?A*×A*,≤是A*上線性序.如果那么(f,g)∈〈S〉.

證明如果f=g,那么顯然(f,g)∈〈S〉.假設.設n≥1是使得的最小數.對n作歸納來證明這一結果.對于n=1的歸納起點,根據定義2.2,存在a,b∈A*和(u,v)∈ΠS使得f=aub且g=avb,因此(f,g)∈〈S〉.對于n＞1的歸納步驟,令

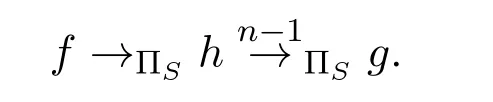
根據歸納假設,可得(f,h)∈〈S〉和(h,g)∈〈S〉,利用同余的傳遞性,可得(f,g)∈〈S〉.

設≤是A*上的線性序.對于由A*上的二元關系S生成的同余〈S〉,定義

對于公式(1)中給出的項重寫系統,記:

它是由A*的在(A*,ΠS)的規范型中的元素構造的集合.

引理3.3設A是集合,S?A*×A*,≤是A*上的線性序.

(a)若(A*,ΠS)是匯合的,則Pm(〈S〉)∩Irr(S)=?.

(b)若(A*,ΠS)是終止的且Pm(〈S〉)∩Irr(S)=?,則(A*,ΠS)是匯合的.

證明(a)若Pm(〈S〉)∩Irr(S),則設w∈Pm(〈S〉)∩Irr(S).因為w∈Irr(S),w在規范型中.又因為w∈Pm(〈S〉),則存在v∈A*使得

由引理3.1,對于任意n≥1和zi∈A*,1≤i≤n,存在一個基本S-傳遞序列w=z1-z2-···-zn=v,連接w到v.則對任意的1≤i≤n-1,

由等式(1),因為w=z1在規范型中,所以有

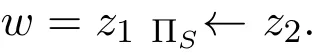
若

則由可得v＞w,這與等式(3)中w＞v矛盾.因此存在最大值i,1≤i≤n-1使得

并且通過可得v＞w,再次與方程(3)中的w＞v矛盾.所以zi+1,即,當i≤n-2,存在zi+2,使得或者對于前一種情況,通過對于后一種情況,因為是一個分叉,w在規范型中,則由(A*,ΠS)是匯合的可得繼續這個過程,最后可得到和v＞w,這與等式(3)中w＞v矛盾.

(b)假設有相反的情形(A*,ΠS)是不匯合的.則存在分叉是不可匯合的.因為(A*,ΠS)是終止的,所以存在u1,v1∈Irr(S),使得u11,由引理3.2,有(w,u1),(w,v1)∈〈S〉,因此(u1,v1)∈〈S〉.從而u1∈Pm(〈S〉)或者v1∈Pm(〈S〉),這兩種情形都與Pm(〈S〉)∩Irr(S)=?矛盾.

引理3.4設A是集合,S?A*×A*,≤是A*上容性良序.則

證明因為Pm(〈S〉),Irr(S)?A*,由此可見Pm(〈S〉)∪Irr(S)?A*.相反地,設u∈A*.由引理2.2可知(A*,ΠS)是終止的,于是u有一個規范型v∈Irr(S),使得若u=v,則u∈Irr(S)?Pm(〈S〉)∪Irr(S),得證.假設u/=v.由引理3.2,可得(u,v)∈〈S〉.因為≤是容許的,所以v＜u,因此

證畢.

引理3.5設A是集合,≤是A*上的容性良序.對于〈S〉的每一個同余類A,有

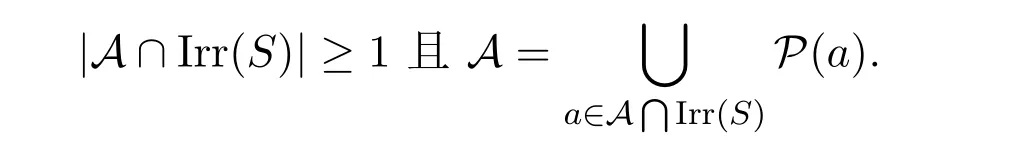
證明由引理2.2可得項重寫系統(A*,ΠS)是終止的.設b∈A.則存在a∈Irr(S)使得由引理3.2,有(b,a)∈〈S〉,從而a∈A.因此且因為由b∈P(a)可得

反之,對任意元素a∈A,由引理3.2可得P(a)?A,從而證畢.

引理3.6設A是集合,S?A*×A*,≤是A*上的容性良序.對于〈S〉的每一個同余類A,若(A*,ΠS)是匯合的,則|A∩Irr(S)|=1.

證明由引理3.5,可得|A∩Irr(S)|≥1.假設有相反的情況|A∩Irr(S)|≥2.令

且|I|≥2,會出現兩種情形.

情形1:對于一些i,j∈I且在這種情況下,存在為一個分叉.因為ai,aj∈Irr(S)且aiaj,所以ai和aj不可匯合,這與(A*,ΠS)是匯合的相矛盾.

情形2:對任意i,j∈I且因為(ai,aj)∈〈S〉,針對引理3.1,存在一個基本S-傳遞序列ai=z1-z2-···-zn=aj,連接ai到aj,n≥1,zk∈A*,1≤k≤n.類似于引理3.3(a)的證明,有

注意到ai∈Irr(S).因此可以選擇?:=max{k|zk∈P(ai),1≤k≤n}.若?=n,則aj=zn∈P(ai),因此aj∈P(ai)∩P(aj),這與P(ai)∩P(aj)=?矛盾.假設1≤?＜n.則

定理3.1設A是集合,S?A*×A*,≤是A*上的容性良序.則以下陳述是等價的.

(a)(A*,ΠS)是收斂的.

(b)(A*,ΠS)是匯合的.

(d)Irr(S)是A*/〈S〉的截面.

證明因為≤是A*上的容性良序,由引理2.2知(A*,ΠS)是終止的.所以(a)和(b)是等價的.由引理3.3,引理3.4可知(b)和(c)的等價性.

((b)?(d))假設(A*,ΠS)是匯合的.根據引理3.6,Irr(S)得每一個同余類恰只有一個元素,所以Irr(S)是A*/〈S〉的截面.

((d)?(b))假設(A*,ΠS)是不匯合的.則存在一個分叉是不可匯合的.因為(A*,ΠS)是終止的,可以假設且有u1,v1∈Irr(S),u11,所以根據引理3.2,有(w,u1),(w,v1)∈〈S〉,所以(u1,v1)∈〈S〉.因此在同一個同余類中Irr(S)包含兩個元素u1和v1,這與Irr(S)是A*/〈S〉的截面矛盾.證畢.

4 應用

在本節中,分別給出由三個元素生成的Plactic幺半群[10]和中國幺半群[22]的截面.

定義4.1設A={x1,x2,x3}.由A生成的Plactic幺半群是A*模去同余〈S〉的商,其中S是Knuth關系:

擴展生成元的集合A:x1＜x2＜x3上的序,為A*裝配一個帶權字典序≤wl.文獻[10]表示與上述S相關的項重寫系統是不收斂的;但在增加三個額外的重寫法則后,它是收斂的.記:

關聯S的項重寫系統(A*,ΠS)是收斂的.

引理4.1[10]用上面的符號,

(a)Plactic幺半群上的項重寫系統(A*,ΠS)是收斂的.

(b)項重寫系統(A*,ΠS)的規范型的集合是

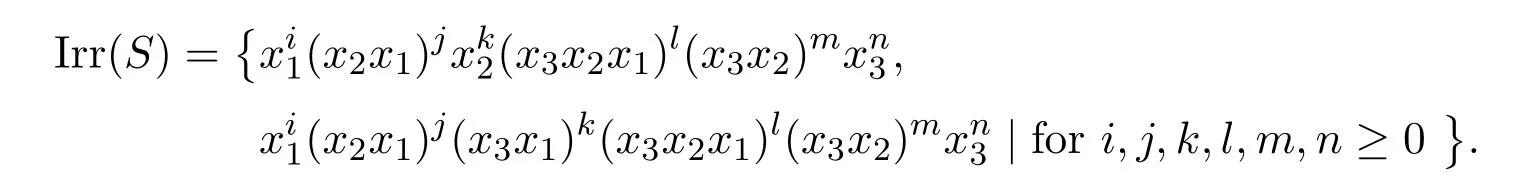
作為該引理的直接結果,有

定理4.1采用上述符號,規范型的集合Irr(S)是秩為3的Plactic幺半群的截面.

證明由定理3.1和引理4.1可得.

接下來,給出了中國幺半群的截面.

定義4.2設A={x1,···,xn}.A上的中國幺半群是自由幺半群A*模掉中國同余〈S〉的商,其中

使用A*上的加權字典序≤wl,它擴展了生成元上的序:x1＜x2＜···＜xn.與上述S相關的項重寫系統是不收斂的;但在添加一個新的重寫法則[22]后,它是收斂的.記:

引理4.2[22]采用上面的符號,中國幺半群的項重寫系統(A*,ΠS)是收斂的.

作為一個直接的結果,有

定理4.2采用上述符號,規范型的集合:是中國幺半群的截面.

證明由定理3.1和引理4.2可得.