不可忽視的科里奧利加速度

陸天明

（南京師范大學附屬中學江寧分校，江蘇 南京 211102）

1 問題緣起

在一次物理競賽教學的課堂上，學生們發現用兩種方法解決一道物理競賽題時，所得到的結果不同，引發了學生的熱烈討論.經過近一節課的研究，問題終于得到了圓滿解釋.原題如下.

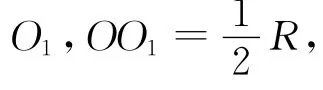
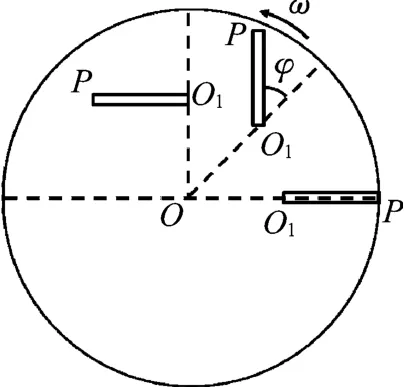
圖1

經過討論，學生對此題大致提出了2種方法.

方法1.因為絕對速度va等于相對速度vr加牽連速度ve，即va=ve+vr，所以有絕對加速度aa等于牽連加速度ae和相對加速度ar之和，即aa=ae+ar.以此出發，可以求出直棒端點P 相對地面的加速度.過程如下.

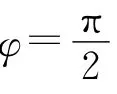
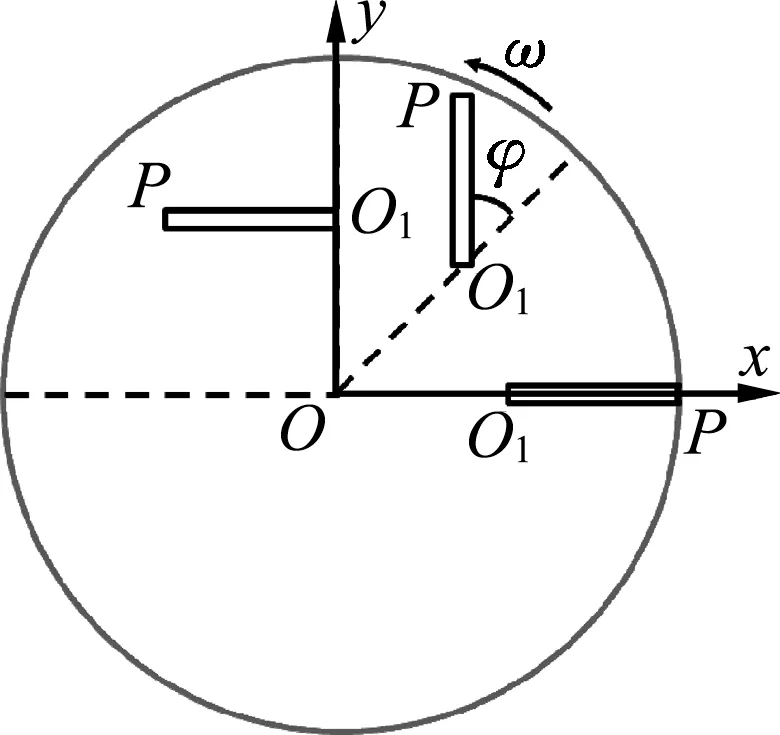
圖2

方法2.以O1為坐標原點，建立一個相對于地面平動的參考系，如圖3所 示，OO1與P 點 在 同 一直線時，由O1指向P 的直線選為x 軸，在圓盤和直棒轉動過程中x、y 軸相對地面方向始終保持不變.不難發現，直棒相對平動參照系x O1y 轉動，且角速度為Ω=2ω.

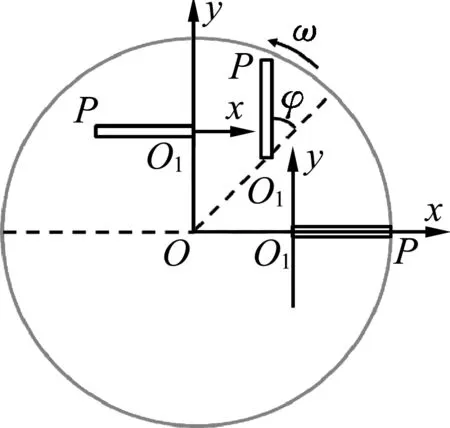
圖3

用兩種方法所得到的結果不同，問題到底出在什么地方呢？

2 問題分析

事實上，方法1 認為P 點繞O1作角速度為ω的轉動，實際上是在O1點固定了一個和圓盤相對靜止的參考系，如圖4所示.這個參考系本身就是一個比較復雜的參考系：相對于固定于O 點的地面參考系（靜系或絕對參考系）.這個參考系既在以角速度ω 轉動，又在隨著O1平動，而方法1正是忽略了這個參考系的轉動所引起的效應.

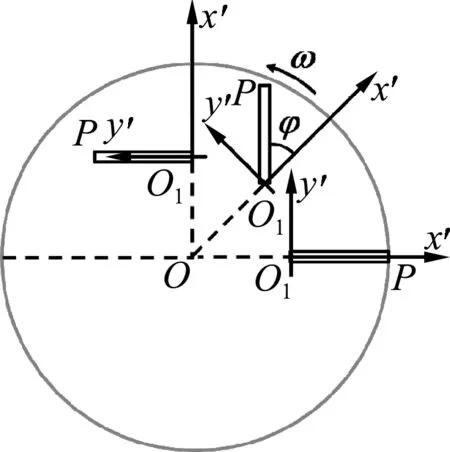
圖4

值得注意的是，我們不能因為有速度公式va=ve+vr，而想當然地認為加速度也有公式aa=ae+ar，實際上aa=ae+ar只對平動參考系適用，在轉動參考系中，還應考慮因為參考系本身轉動而引起的科里奧利加速度ac.轉動參考系中的加速度變換到絕對參考系時，加速度的表達式為

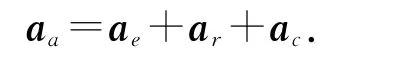
但是，如果按照方法1的思路，在O1點固定了一個和圓盤相對靜止的轉動參考系，那么運算會比較繁瑣，最好的方法是直接在O 點建立固定于圓盤的轉動參考系.

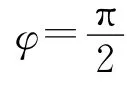
如果在O1點固定一個和圓盤相對靜止的轉動參考系，那么如何進一步運算，這個問題可以留給學生思考和練習.實際上，運算過程會比上面的過程復雜.

3 結語

以上對P 點運動的分析，有兩種參考系選擇：方法2把O1作為中間參考系，但它是一個平動參考系，兩軸保持和x 軸、y 軸平行，所以這個中間參考系相對O 系是平動的參考系，不會出現科里奧利加速度.方法3建立固定于O 點的轉動參考系，O1是這個轉動參考系中的另一個不動點，P“相對O1”其實是原來問題中設定的中間過渡，沒有O1無法說明P 點在圓盤里是怎樣運動的，P 相對固定于O 點的轉動參考系有相對運動，所以出現科氏加速度.

方法2和方法3給出了平動和轉動參考系下的同一個點運動的加速度的不同表示，但又殊途同歸.另外，筆者不選擇在O1處固定一個隨圓盤轉動的參考系，原因是運算會麻煩一些.

科里奧利加速度比較抽象、難懂，一直是物理競賽教學的難點，對學生所犯錯誤的討論不失為突破這個難點的一個好方法.通過討論，可以加深學生對科里奧利加速度的理解，促進深度學習的發生.實際上，學生在學習中所犯的錯誤應是我們教學的寶貴資源，充分利用這類資源不僅可以讓學習更具深度，還可以讓我們的教學更加生動活潑.