化“變”為“定” 尋找極值條件
——對一道競賽題的深入探析
高 振
(山東省平邑縣教育和體育局教研室,山東 臨沂 273300)
1 原題再現
例題.(2019年第36屆全國中學生物理競賽山西賽區預賽第11 題)有一寬為l、高為2l的墻壁,如圖1所示.現從墻壁左側地面發射一個質量為m 的小球(可視為質點),使小球越過墻壁,擊中墻壁右側地面上的目標S.目標S 與墻壁中心線的距離為d.不計空氣阻力.

圖1 題目圖示
(1)小球有最小動能時,發射點與墻壁中心線的距離為多少?小球能夠擊中S 的最小初始速度與地面的夾角θ 為多少?
(2)若不需擊中S,僅要求小球能夠越過墻壁,求小球發射的最小動能,以及初始動能最小時發射點與墻壁中心線的距離為多少?
參考答案和許多師生在解答該題時,都未作分析論證直接認定(極值條件):擊中目標或不需擊中目標時,由于要求初動能最小,此時拋物線應該恰好過墻壁的兩個角.兩問均以上述極值條件作為解題的出發點,計算的結果為(計算過程略)
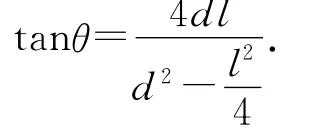

點評:該題以學生熟悉的拋體運動為背景,附加了小球越過墻壁的限制條件后,又在兩小問中分別附加了需要擊中目標或不需擊中目標的限制條件,并提出了小球初動能最小(又一限制條件)的極值問題.在熟悉的拋體運動中添加多種“佐料”(3個維度的限制條件),這樣巧妙地設計題目,使得原本師生以為熟悉而又平淡的拋體問題,變得極具趣味性和挑戰性.體現了命題人高超的命題技巧和獨具匠心的問題設計能力,是一道難得的好題.
由于該題以小球越過墻壁、擊中或不擊中目標、初動能最小等3個維度的限定下,要求考生分析求解極值問題.由于題目變化的因素多,尋找小球初動能最小的極值條件成了該題的難點,普遍反映該題難度大.
俗話說“好馬要配好鞍子”,一道設計精巧的高難度好題,好比是一匹寶馬,更需科學合理的解答,才算得上是“好馬要配好鞍子”“錦上添花”.下面對該題難點——兩小問中小球初動能最小的極值條件,分別做嚴密的分析論證.
2 分析論證兩小問中小球初動能最小的極值條件
對于這樣復雜多變(指題目中變化的因素)的物理問題,巧妙地應用物理學思想方法,從不同的視角去思考,找到恰當的途徑,化“變”為“定”,減少問題中的變化因素,使問題變得簡單明朗,才能順利實現突破該題難點,找到小球初動能最小的極值條件的突破口.
2.1 用轉化法化“變”為“定”,尋找不需擊中目標時小球初動能最小的極值條件
當不需擊中目標時,學生往往從地面上小球的發射點觀察,發射點離墻壁的距離是變化的,發射速度方向與地面的夾角是變化的,同時還要滿足小球越過墻壁這一限制條件.這樣諸多的變化因素中,小球初速度最小的極值條件并不是顯而易見的.
要減少上述諸多的變化因素,就要化“變”為“定”,就要應用轉化法轉化觀察的視角,引導學生從與墻壁等高的水平面上觀察(換角度思考),則容易看出小球越過墻壁的任意一條拋物線與墻壁等高的水平面的交點P、M 在墻角B、C 兩點連線的外側區域里(包括B、C 兩點),如圖2所示.

圖2 與墻壁等高的水平面上觀察
顯然,只要P 點到M 點的距離xPM(變化)不小于墻壁寬度l(確定),小球一定能越過墻壁,則小球越過墻壁的條件為

由于不需擊中目標,則小球發射點到墻壁中心線的距離x 可以由近及遠地變化,使得小球在P 點的速度方向連續變化,即P、M 兩點(由于等高,關于拋物線對稱軸對稱)的速度方向與水平面的夾角θ滿足

(注意:在不需擊中目標的條件下,理解θ角滿足(2)式是很重要的!)
設P 點的速度大小為vP,P 點到M 點的運動時間為t.則水平方向

由(1)、(2)、(5)式可知:當取xPM=l 最小值(此時P、M 點分別與B、C 點重合,拋物線的對稱軸就是墻壁寬度l的中垂線),且取sin2θ=1最大值(此時θ=45°)時,vP有最小值,即小球在墻角B點速度的最小值為

當小球在B 點的速度最小時,由機械能守恒可知小球在發射點的速度也最小.
上述分析論證表明:不需擊中目標時,參考答案第(2)問中的極值條件“要求初動能最小,此時拋物線應該恰好過墻壁的兩個角”是正確的.
關于該題第(2)問的教學,筆者不主張憑物理直覺猜想得到上述極值條件,應該把教學的重點放在引導學生應用科學思維方法,進行嚴密的分析論證,從而找到發射小球初速度最小的極值條件.這樣,不僅能有效地訓練學生思維的靈活性、深刻性以及應用數學知識解決物理問題的能力,還能順利地想到下面的不同于參考答案和文獻[1]的更加突出物理本質的求解思路.

(8)式、(11)式分別與參考答案中的(3)式、(4)式相同,也與文獻[2]3種解法的結果一致,殊途同歸.
2.2 用逆向思維化“變”為“定”,尋找需要擊中目標時小球初動能最小的極值條件
當需要擊中目標時,受思維定勢的影響,學生仍然會在與墻壁等高的水平面上觀察.可是,在需要擊中目標的條件制約,圖2中小球在P 點的速度方向不再連續變化,即P、M 兩點的速度方向與水平面的夾角θ 已經不滿足(2)式了,因此無法用(5)式得出小球初動能最小的極值條件.已有的舊方法在第(1)問中失靈了,應該另辟蹊徑,尋找第(1)問需要擊中目標的限定條件下小球初動能最小的極值條件.
第(1)問中小球越過墻壁并擊中目標的過程中,小球的發射點的位置在變化,發射點到墻壁中心線的距離也在變化.但是,若應用逆向思維,從擊中的目標S 出發逆向觀察,可以達到化“變”為“定”的目的,即目標S 到墻壁兩側面的距離都確定,如圖3所示.從擊中的目標S 出發逆向的運動中,很方便的定量表達小球越過墻壁的條件.
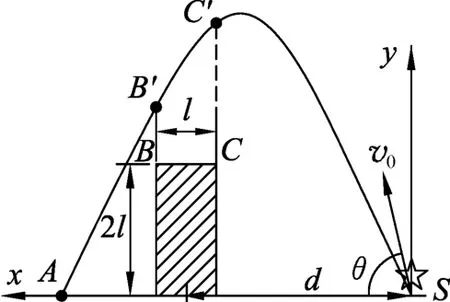
圖3 發射小球擊中目標的逆過程
根據拋物線的對稱性,A 和S 兩點的速度大小相等為v0,與地面的夾角θ也相等,設小球從S到C′和從S 到B′的運動時間分別為t1、t2.
要使小球越過墻壁(逆向運動已保證了“擊中目標”),必須使拋物線上B′、C′兩點的縱坐標yB′≥2l、且yC′≥2l.豎直方向小球做勻減速直線運動,則小球越過墻壁的條件為

至此,細心的讀者可能已經看出了參考答案中第(1)問的極值條件是錯誤的.因為參考答案第(1)問在需要擊中目標時,直接認定“由于要求初動能最小,此時拋物線應該恰好過墻壁的兩個角.”這相當于在圖3中直接認定B′、C′兩點分別與B、C 兩點重合,也相當于把不等式(12)、(13)式當成了等式,然后由(12)—(15)式4個方程直接 消 去v0、θ、t1、t24 個 未 知 量 中 的3 個 解 得 第4個未知量,并沒有對初速度平方v02做數學極值分析.
下面由(12)、(13)式2個不等式,當θ取何值時,初速度平方v02取最小值,做嚴密的數學極值分析.
將(14)、(15)式中的時間分別代入(12)、(13)式,并兩式相加整理得


把(19)、(20)式 代 入(25)式 所 得 結 果(表達式很繁,這里未寫出,讀者可驗證)與參考答案中的x=d 不同.這又表明:需要擊中目標時,參考答案中的極值條件“由于要求初動能最小,此時拋物線應該恰好過墻壁的兩個角”是錯誤 的.[1]

