立式四軸艙體內腔加工專機機械動力學建模與分析＊

李凌霄 成群林 平 昊 袁楨棣 葉 磊

（上海航天精密機械研究所，上海 201600）

隨著我國航空航天技術的發展，越來越多的新結構、新工藝正應用在各類回轉體類航天產品中。例如航天薄壁類圓形艙體的內壁需要鏜銑加工，艙體內腔存在許多凸臺、零件安裝面和通孔等特征需要加工[1]。內腔加工專機是能夠滿足此類機加工需求的專用設備，已經得到了廣泛應用。

航天典型產品的內腔加工，刀具路徑為復雜空間軌跡，加工中專機的動態誤差遠遠超過幾何誤差等靜態誤差，是影響加工誤差的主要因素[2]。對內腔加工專機開展機械動力學特性的研究與分析是加工動態誤差辨識與補償，提高內腔加工精度與產品質量的前提。目前工程中對內腔加工專機進行動力學建模的普遍方法是，設置專機CAD 模型的材料數據與剛性接觸，采用有限元分析軟件求解固有頻率與振型[3-4]，分析動力學特性。但是，這種簡化假設沒有考慮專機結合部的動態剛度特性，根據研究統計，機床整機60%～80%的剛度來自各種結合部[5]。因此無論是從專機設計、裝配和動特性分析，還是從結構修改、建立虛擬樣機來說，必須考慮專機結合部的動態剛度特性[6]。而且采用有限元分析軟件進行的機械動力學建模分析為離線模型，不適用于數字孿生技術中虛擬實體鏡像物理實體，數據實時交互的研究[7]。

本文以立式四軸艙體內腔加工專機為研究對象，基于動態子結構法建立機械動力學模型，求解了專機結合部的滾珠絲杠副、直線導軌副動態剛度。應用有限元軟件建立專機有限元模型，求解結合部剛性接觸與設定動態剛度性的整機固有頻率與振型，最后對專機進行諧響應分析求解了加工振動激勵下的專機響應。

1 基于子結構法的機械動力學建模

立式四軸內腔加工用于加工大直徑尺寸艙體，如圖1 所示主要由床身、立柱、滑枕、工作臺和主軸部件組成，其中床身為T 型底座與橫梁的固連的整體。各部件由伺服電機通過絲杠螺母機構驅動，在直線導軌上往復運動，并通過光柵尺實現閉環控制，實現四軸聯動加工。滑枕上安裝有第二回轉軸用于適當調節主軸角度，適應特定艙體內腔加工面。根據專機驅動形式，可劃分為床身、立柱、滑枕、工作臺和主軸5 個子結構。

圖1 立式四軸艙體內腔加工專機的部件構成

建立如圖2 所示坐標系，其中A軸不作為四軸聯動軸。可以分析得知專機的剛性結合部有床身與機床墊鐵的地腳螺栓結合部，滑枕與主軸的螺栓連接剛性結合部。專機的動結合部有X軸的工作臺與床身的絲杠螺母副、直線導軌副結合部；Z軸的立柱與床身的絲杠螺母副、直線導軌副結合部；Y軸的立柱與滑枕的絲杠螺母副、直線導軌副結合部。

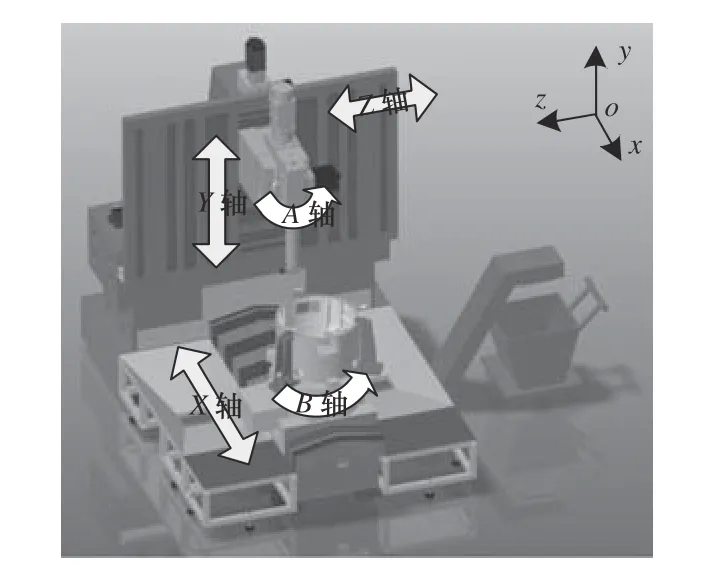
圖2 立式四軸艙體內腔加工專機的坐標系建立

以機床床身底部的端點作為整個坐標系的原點，根據振動特點，將機床簡化為具有20 個自由度的集中參數動力學模型，各自由度的分配如下：

q1為 床身沿y軸的平動坐標y1；q2為床身繞z軸的轉動坐標 θz1；q3為 床身繞x軸 的轉動坐標 θx1；q4為立柱沿x軸的平動坐標x1；q5為立柱沿y軸的平動坐標y2；q6為 立柱繞x軸的轉動坐標 θx2；q7為立柱繞z軸的轉動坐標θz2；q8為滑枕沿x軸的平動坐標x2；q9為滑枕沿z軸的平動坐標z1；q10為 滑枕繞y軸的轉動坐標θy1；q11為滑枕繞z軸的轉動坐標 θz3；q12為主軸沿x軸的平動坐標x3；q13為 主軸沿y軸的平動坐標y3；q14為主軸沿z軸的平動坐標z2；q15為主軸繞x軸的轉動坐標 θx3；q16為主軸繞z軸的轉動坐標θz4；q17為工作臺沿y軸的平動坐標y4；q18為工作臺沿z軸的平動坐標z3；q19為 工作臺繞x軸 的轉動坐標 θx4；q20為工作臺繞z軸的轉動坐標 θz5。

依照劃分的子結構、建立的坐標系，得到內腔加工專機機械動力學建模系統簡圖如圖3 所示。

圖3 中ci為各子結構質心，ai、bi與di為各子結構質心相對位置關系。

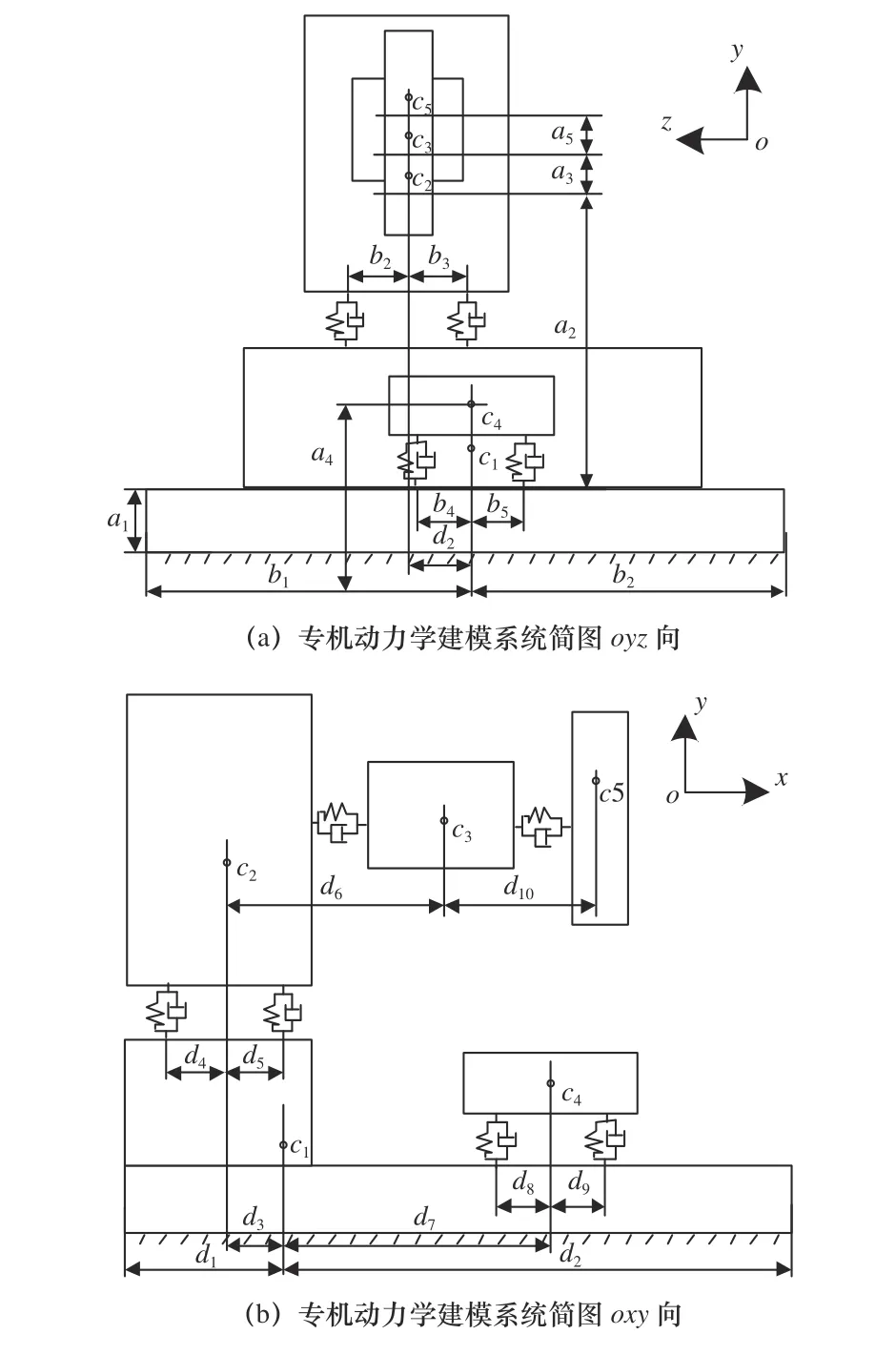
圖3 專機動力學建模系統簡圖

用拉格朗日方程建立系統的運動方程，拉格朗日方程的一般表達式[8]為

式中：U、D分別為系統的總勢能、瑞利耗能函數。

根據動力學模型，算得T、U、D，系統的總動能為

系統的瑞利耗能函數為

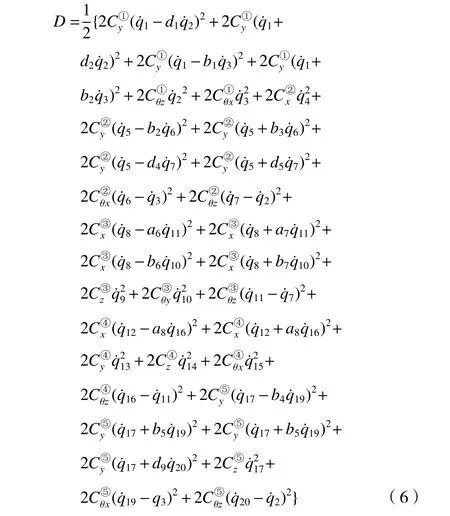
式（4）～（6）中，mi（i=1,2,···,5）依次為5個子結構：床身、立柱、滑枕、工作臺和主軸的質量；Iφi（φ=x,y,z，i=1,2,···,5）為5 個子結構繞各軸的轉動慣量；（ω=x,y,z，α=①,②,···,⑤）為5 個動結合部的各向線剛度；（ω=x,y,z，α=①,②,···,⑤）為5 個動結合部的各向角剛度；同理，C為各結合部阻尼。

將式（4）～（6）代入式（3）中，整理后得專機動力學方程

2 專機結合部的剛度求解

式（5）中專機的動力學方程中各項剛度參數為各結合部參數，專機的各種結合部可以分為子結構螺栓連接的剛性接觸結合部、各移動軸由滾珠絲杠副和直線導軌副組成的動結合部，針對各結合部特點，開展求解。

2.1 剛性結合部的剛度

專機的剛性接觸部即螺栓結合部剛度由吉村允孝法[9]求解，根據螺栓參數、等效元素個數由吉村允孝法得表1。

表1 專機剛性結合部剛度

2.2 滾珠絲杠副的剛度

對于動結合部進行動力學建模分析，滾珠絲杠副軸向剛度kx為與滾珠絲杠副相關聯的零部件剛度的串聯總和[10]，絲杠副主要由軸承、絲杠和螺母組件組成，其動力學模型如圖4 所示。

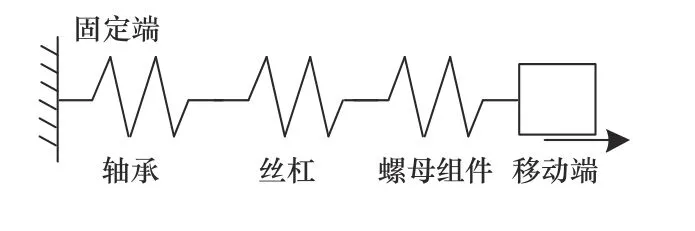
圖4 滾珠絲杠副的動力學模型

由此得到絲杠傳動系統的軸向剛度kx可表示為

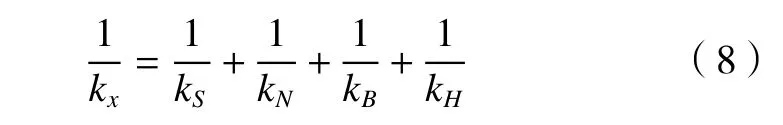
式中：kx為滾珠絲杠副的軸向剛度；kS為絲杠軸的軸向剛度；kN為螺母組件的軸向剛度；kB為支撐軸承的軸向剛度；kH為螺母座的剛性，N/μm。

絲杠的安裝方式為兩端固定，絲杠軸的軸向剛度由下式求得

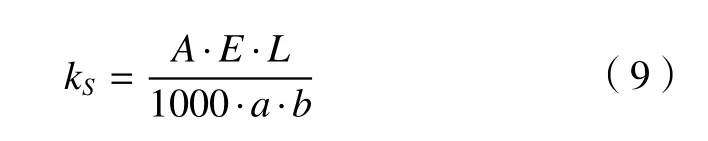
式中：A為 絲杠軸的斷面面積，mm2；E為絲杠軸的楊氏模數；L為安裝間距，mm；a與b為螺母距兩端面的距離，mm。當在a=b=的位置時，kS的值為最小，軸向彈性位移量最大為

螺母的軸向剛性kN，支撐軸承的軸向剛性kB與螺母座的軸向剛度kH可通過查詢THK 手冊曲線結合機床螺母預壓情況、使用情況得出[11-12]。綜合以上絲杠螺母的各組成部分剛性，代入式中即可求解絲杠螺母動結合部的軸向剛性。

絲杠螺母動結合部的法向剛性計算方法由基于赫茲基礎理論法[13]求解，這里不再贅述。

得到絲桿螺母動結合部的剛度，其中：軸向剛度kx=3.76×105N/mm，法向剛度為ky=kz=2.13×106N/mm。

2.3 直線導軌副的剛度

建立直線導軌的動力學模型如圖5 所示。

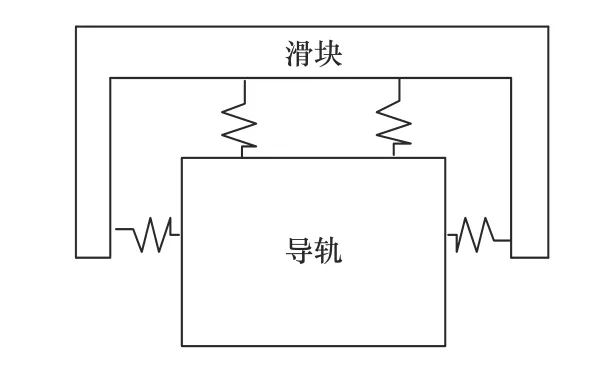
圖5 直線滾動導軌動力學建模

滾動導軌承受負荷時，鋼球、滑塊在容許負荷范圍產生彈性變形[14]。這時的形變量與外加負荷之比率就是剛性。由于滾動導軌的徑向間隙影響剛性，因此機床選THK 品牌標準的C0 間隙即中預壓，為適用于加工中心的預壓種類。根據選定的間隙標準、滑塊形式，查詢手冊可以得到直線導軌的剛性kx′，直線導軌的法向剛度求解方法與滾珠絲杠相同。

得到直線導軌動結合部的剛度為：軸向剛度kx=2.53×105N/mm，法向剛度為ky=kz=4.78×106N/mm。

將絲杠螺母剛度與直線導軌剛度代入式（5）即可得到專機考慮了動結合部剛度的動力學方程。

3 內腔加工專機動力學特性分析

3.1 應用動態子結構法求解固有頻率

多自由度系統的固有頻率是通過求解系統的無阻尼自由振動方程得到的[15]。多自由度系統無阻尼自由振動的運動方程可由式（7）中令C20×20=[0]、Q20×1=[0]，得

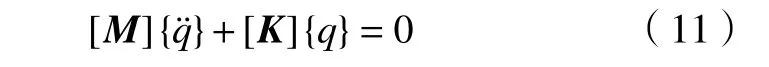
式中：[M]為 專機的質量矩陣；[K]為專機剛度矩陣，q為系統的廣義坐標。

設方程的解為

式中：{A}為 系統自由振動時的振幅向量；ωn為振動頻率，t為時間。

將由式（12）及其對時間的二階導數代入式（11）中，消去因子后得

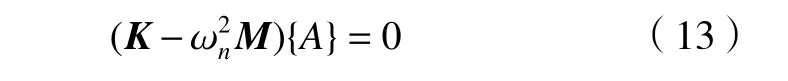
求解式（13）常稱為特征值問題。要得到振動解（非零解），必須 {A}的系數行列式等于零，即

式（14）中剛度矩陣K各元素均已求得，質量矩陣M中子結構的質量及轉動慣量由三維建模后設置密度，經CAD 軟件求解得到，如表2 所示。

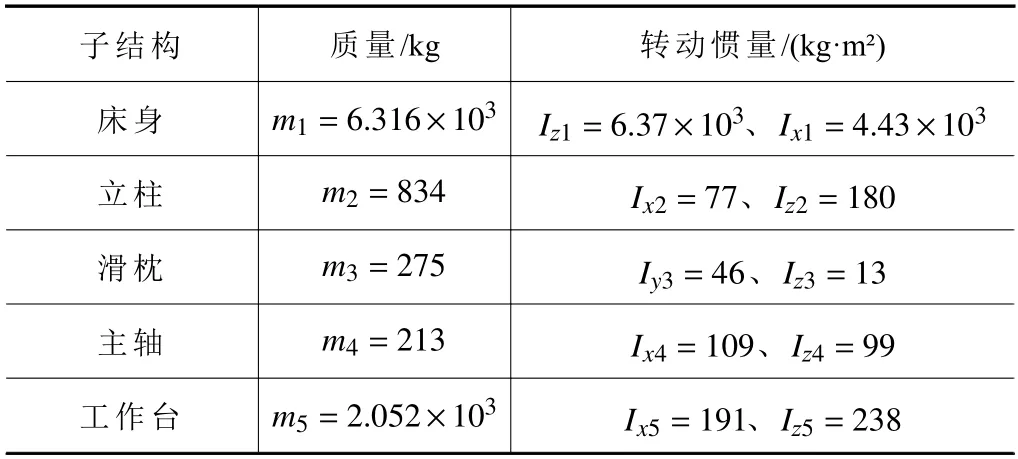
表2 機床子結構的質量及轉動慣量

計算式（14）即可得到基于動態子結構法的專機前四階固有頻率為：35.1 Hz、36.9 Hz、76.4 Hz和73.7 Hz。

3.2 應用剛性簡化的有限元分析求解固有頻率

在實際機械設備設計中，通常不會考慮動結合部的剛性問題，將所有結合部都按照剛性固定方式處理[16]。采用剛性簡化的方式，基于有限元軟件求解專機的固有頻率。

首先對專機進行合理簡化，去除模型中的螺紋凸緣等特征，其中電機、轉臺、加長桿角度頭、刀具和卡盤等部件采用實體建模、抽殼特征處理。設置材料屬性如表3 所示。

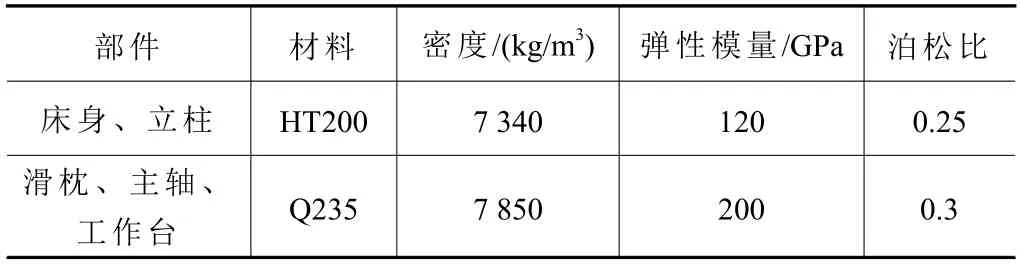
表3 有限元仿真部件材料屬性設置

將三維模型導入有限元軟件中建立有限元仿真模型，設置所有結合部剛性接觸，劃分網格如圖6所示。

圖6 基于有限元軟件的內腔加工專機有限元建模

模態分析求解的邊界條件設置為床身底面與墊鐵的接觸面固定。求得基于動態子結構法的專機前四階固有頻率為：40.2 Hz、42.9 Hz、90.6 Hz 和91.7 Hz。

3.3 應用設置動結合部剛度的有限元法求解固有頻率

為驗證建立考慮動結合部剛性的子結構動力學模型正確性，利用有限元軟件設置動結合部剛性，為簡化計算處理，將各子結構接觸面處剛性固連，在滾珠絲杠副及直線導軌處設置動結合部，求解專機固有頻率。模態分析的材料設置、網格劃分及邊界條件與剛性簡化計算一致。

設置專機的動結合部（X軸的工作臺與床身的絲杠螺母副、直線導軌副結合部；Z軸的立柱與床身的絲杠螺母副、直線導軌副結合部；Y軸的立柱與滑枕的絲杠螺母副、直線導軌副結合部）的剛度進行模態分析。代入動結合部法向與切向的剛度，如圖7a 所示，在各絲杠螺母副的結合處設置3 個彈簧單元模擬結合部剛度。

如圖7b 所示，以床身與工作臺的動結合部為例，以床身絲杠螺母與工作臺、床身導軌與工作臺滑塊的接觸面法向建立X方向彈簧單元，以右手系建立X方向、Z方向彈簧單元。設置所有彈簧單元的剛度，完成動結合部剛度定義。

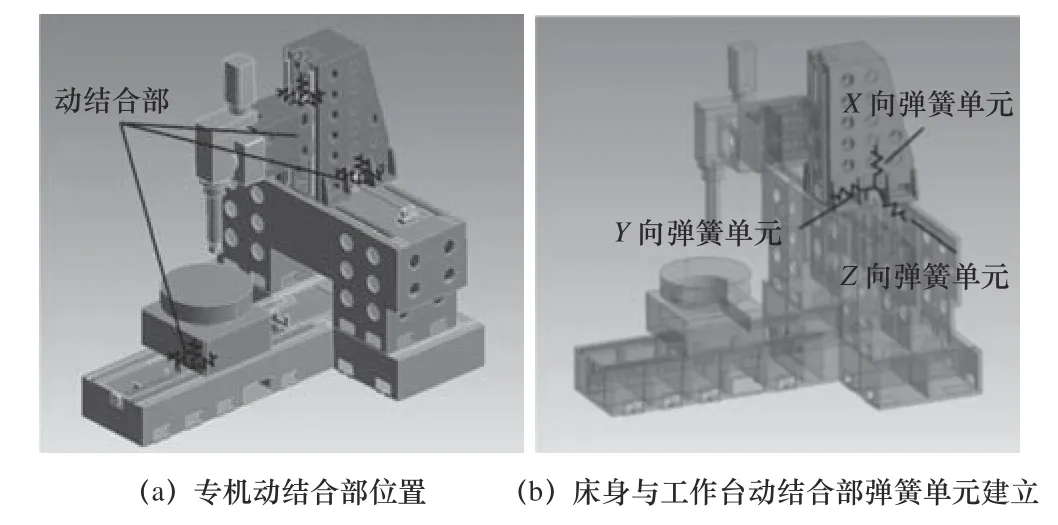
圖7 專機動結合部設置

由此可以求解專機含動結合部剛度的固有頻率為34.2 Hz，38.2 Hz、78.6 Hz 和79.4 Hz。

專機的前四階振型如圖8 所示。

從圖8 可知專機的機械動力特性，一階振型為立柱與主軸頭繞Y軸的偏擺，二階振型為立柱與主軸頭繞Z軸的轉動，三階振型為立柱與床身繞Z軸的扭轉，四階振型變化為主軸頭滑枕繞X軸的扭轉。根據固有頻率與振型分析研究結果表明：（1）主軸部件的動力響應對刀尖點的動力響應貢獻最大，應選用高剛性的鏜銑動力頭、加長桿角度頭，并加強主軸部件與A軸回轉臺的剛性連接。（2）立柱組件與床身組件的動結合處中導軌滑塊的跨距較小，致使二階振型立柱組件繞Z軸轉動幅度較大，應在該處選用高剛性大尺寸導軌滑塊，并適當增大跨距。針對上述結構修改后，較大幅度提高了整機的動態性能。

3 種求解方法得到的專機前四階固有頻率為如表4 所示。

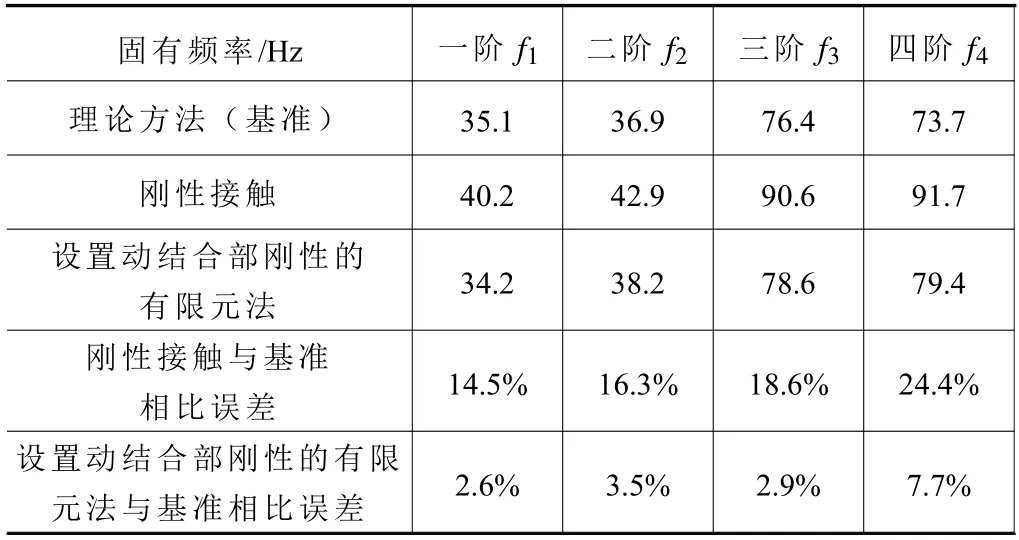
表4 含動結合部剛度求解的專機固有頻率

可以看出，結合部動態參數的描述是影響機床整機動力學性能的重要因素，特別是對于高階固有頻率特性計算，影響更為明顯。因此研究動結合部的動態剛度，對于求解機床動力學特性有著重要意義。由表4 的數據可知，本文建立的考慮結合部動態剛度的子結構法可以正確求解專機動力學模型，求解固有頻率與振型，建立的動力學方程可以應用到數字孿生動力學仿真應用中。

3.4 內腔加工專機的諧響應分析

模態分析只能求得設備本身的固有頻率與振型，而諧響應分析可求得機床在不同頻率簡諧載荷作用下的位移響應，對于分析加工過程中刀具振動對專機加工精度的影響具有重要意義。

在刀具刀尖部添加大小為F=F0sinωt，F0=200 N，方向垂直于動平臺的應力幅值；簡諧力的頻率變化范圍為0～200 Hz（專機工作中刀具與工件振動激勵的頻率范圍）；設置載荷子步數為50；其余邊界條件按計算的動結合部剛性設置（理論方法）。得到刀尖點處X、Y、Z的3 個方向上的位移響應結果（振幅與頻率的關系）如圖9 所示。

圖9 內腔加工專機的刀尖點幅頻特性曲線

在激勵頻率為38 Hz、79 Hz 時響應較大，并且刀尖點X、Y、Z三個方向均產生了較大響應，在其他頻率處沒有發生共振，并且38 Hz 與機床前兩階固有頻率吻合，79 Hz 與第三階固有頻率相吻合，為該機床的敏感頻率，因此在專機在機加工時應避開上述振動頻率，從而保證加工精度和效率。

4 結語

本文基于動態子結構法對立式四軸艙體內腔加工專機進行機械動力學建模，求解了專機動結合部滾珠絲杠副和直線導軌副的動態剛度特性。結果顯示建立的含動態剛度的動力學模型能夠有效鏡像專機動力學特性，可以準確表達專機的真實動態性能，可應用于專機的動力分析與數字孿生虛擬樣機研究。