基于自編碼器的矢量地圖零水印算法

奚 旭,張 新 長,梁 偉 東

(1.蘇州科技大學地理科學與測繪工程學院,江蘇 蘇州 215009；2.廣州大學地理科學與遙感學院,廣東 廣州 510006；3.廣州市城市規劃設計有限公司,廣東 廣州 510030)

0 引言

數字水印作為信息安全防護的前沿技術，在矢量地圖的版權保護中發揮重要作用，有效促進了矢量地圖的安全共享[1-3]。但傳統的嵌入式水印算法不可避免地會影響矢量地圖的精度，從而影響數據的可用性，因此，具有無損性質的零水印算法越來越受到關注[2-7]。零水印算法不修改被保護數據的任何信息，通過提取數據的重要特征構建水印，并依托權威的第三方保存和驗證版權信息[8,9]，顛覆了傳統水印的嵌入機制，實現了對數據的零干擾，非常契合矢量地圖的使用需求。

目前，矢量地圖的零水印研究已取得豐碩成果。例如：李文德等[10]將相鄰特征點構成的直線斜率調制成二值矩陣作為特征信息，與二值版權信息異或生成零水印，該方法對旋轉、平移、縮放以及壓縮簡化有良好的魯棒性；Wang等[11]用同心圓將矢量地圖分為多個環，以每個環中的頂點數作為特征信息構建零水印，該方法對平移、縮放、旋轉、隨機噪聲和裁剪等攻擊有較強的魯棒性；Peng等[12]利用各特征點到矢量地圖幾何中心的距離比作為特征信息構建零水印，利用特征點距離比的幾何不變性提升水印方案性能。以上研究均通過挖掘統計信息實現零水印算法，利用統計信息的穩定性提升算法的魯棒性。此外，部分學者基于頻率域構建零水印，如呂文清等[13]將特征點的DFT相位按符號值轉為二值矩陣作為特征信息構建零水印，該方法在平移、縮放、坐標點增減等方面表現出很好的魯棒性；李文德等[14]將DFT的相位由弧度值轉換為角度值，并選取均勻分布的角度值取整轉化為二進制特征值構建零水印，同樣繼承了DFT系數不變性的優點；韓志聰[15]對特征點進行DWT分解，利用DWT的低頻系數構建零水印，在抗簡化、裁剪、平移、縮放等方面有較好的魯棒性。基于頻率域的零水印繼承了頻率域系數的幾何不變性，但也是一種特殊的統計特征零水印，對應的水印算法也具有鮮明的幾何穩定性。

綜上，挖掘穩定的特征信息是零水印算法的基礎，目前研究集中在穩定統計信息的構建與挖掘，方式單一易導致針對性攻擊，故本文結合深度學習方法中的自編碼器(Auto Encoder，AE)挖掘矢量地圖中深層、穩定的內蘊特征，構建一種魯棒性較強的零水印算法，為地理空間數據版權保護提供技術參考。

1 自編碼器及其在水印算法中的可行性

1.1 自編碼器工作原理

自編碼器是深度學習的重要組成模塊[16]，其核心思想是對原始輸入值進行特征映射(編碼)，通過反向傳播算法的訓練，將其重構為輸出值且盡可能等于輸入值。自編碼器結構(圖1)是包含輸入層、隱藏層和輸出層的3層神經網絡，輸入層與輸出層規模相同，一般情況下隱藏層的神經元節點數量少于輸入層，可得到輸入層的壓縮表示。自編碼器工作原理為：1)設未標簽數據集X(X={x1,x2,…,xn}，n為輸入層神經元節點數量)為輸入層，隱藏層由m個神經元節點構成，一般情況下n>m，利用式(1)進行映射，其中激活函數(Sigmoid函數或Tanh函數)用于進行非線性映射，得到X的特征表達，即隱藏層layer_hide；2)對隱藏層利用式(2)重構輸出層Y，神經元節點數量同樣為n；3)使用重構代價函數(式(3))計算輸入和輸出間的誤差；4)通過誤差反向傳導和批量梯度下降法，迭代尋找最優的G和B，使輸入與輸出間誤差最小[17]。

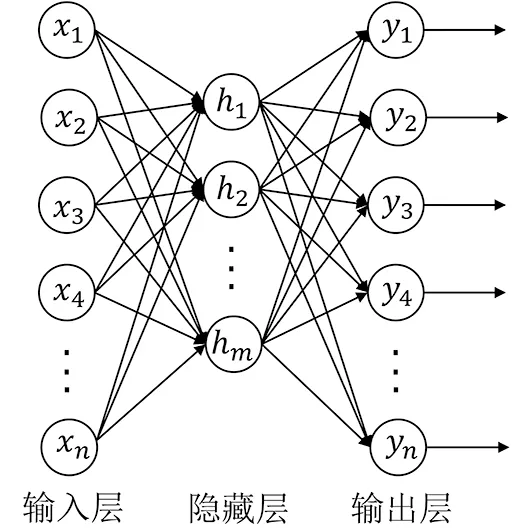
圖1 自編碼器結構Fig.1 Structure of Auto Encoder

(1)

式中：Ge、Be分別為隨機生成的權值矩陣和偏置矩陣，激活函數選用Sigmoid函數。

(2)

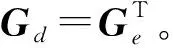
(3)

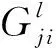
1.2 可行性分析

1個隱藏層對輸入數據的特征提取能力有限，若將多個自編碼器堆疊，則抽取能力會更強大，這種多層自編碼器稱為棧式自編碼器(Stacked Auto Encoder，SAE)，其結構如圖2所示。棧式自編碼器工作原理與自編碼器相似，采用無監督的逐層貪婪訓練法，輸入原始數據X，在第一隱藏層編碼壓縮得到X的一階特征h1；將該特征作為第二隱藏層的輸入，編碼壓縮后得到二階特征h2；經過多次編碼壓縮，最終得到的特征即為X的深層特征描述。在此基礎上將最后一層的輸出與X進行誤差逐層反向傳播，對各隱藏層參數進行有監督的微調。

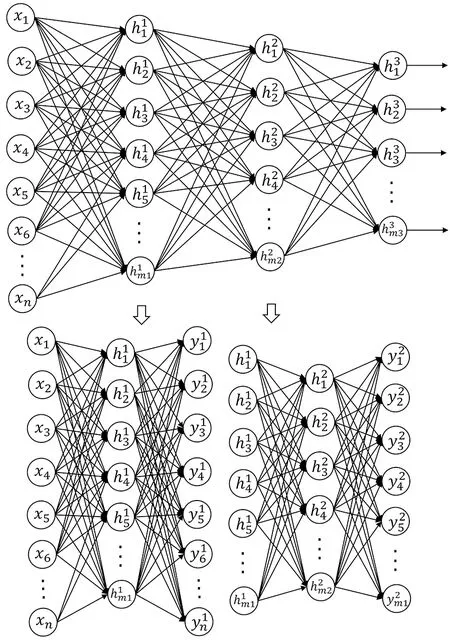
圖2 棧式自編碼器結構Fig.2 Structure of stacked Auto Encoder

自編碼器作為一種無監督學習方法，與其他無監督學習方法有相似之處：若激活函數使用線性函數，重構代價函數使用平方誤差，則其原理類似于主成分分析；若激活函數使用量化編碼，重構代價函數使用平方誤差，則與K-means聚類等相似[18]。但自編碼器與K-means聚類不同之處在于，前者用于提取數據中的高階特征，同時，有學者發現自編碼器的數據壓縮能力優于主成分分析[19]。綜上，自編碼器的結構簡單，對數據能進行有效壓縮，并提取出數據深層、穩定的特征，因此，將自編碼器運用到水印算法中具有可行性。

2 基于自編碼器的矢量地圖零水印構建

本文選用棧式自編碼器對矢量地理數據提取特征信息，因其多應用于圖像識別和分類領域，算法中部分內容(如使用softmax分類、參數微調操作等)可在水印構建過程中略去，另外，自編碼器應用于圖像分類時需要較多的訓練數據，而在水印算法中，可構建的訓練數據受到一定限制，所以在模型訓練中采用放回式訓練。

2.1 零水印構建

本文提出的基于自編碼器的零水印算法實現流程(圖3)為：1)水印圖像生成及處理：生成包含版權信息的二值水印圖像W，大小為p×p像素；為提升安全性，對其進行Arnold置亂[20]，生成加密水印圖像WA，并按照一定規則讀取WA灰度值，轉為水印矩陣WM；灰度值為255，則WM內元素記為1，其他不變，形成由0與1構成的初始水印序列。2)特征點提取：為提升水印算法抗坐標點攻擊的能力，對原始矢量地圖DO采用道格拉斯—普克算法提取特征點，算法的閾值設為τ，可得特征點集合Vτ={v1,v2,…,vi,…,vn}，n為特征點數量。3)特征信息構建：根據式(4)計算Vτ中各特征點的橫縱坐標之差，對Vτ各點坐標差值的數值大小進行排列，按式(5)取其整數部分末兩位，轉為二進制，組成坐標差序列集C={C1,C2，…,Ci，…,Cn}。4)模型訓練集生成：坐標差序列集C的長度為dC，設自編碼器模型訓練集中各圖像大小為d×d，則轉化為一維序列后，其長度為d2，按式(6)對C進行補位操作。將C分為3個序列C1、C2、C3，并均轉化為d×d的二維矩陣，再將矩陣圖像化，各二值圖像組成模型的訓練集L。5)模型訓練：新建一個空白矩陣，行列大小由訓練集L的圖像數量和d2決定；模型讀取L各訓練圖像后，將其轉成長度為d2的一維序列，逐行寫入空白矩陣中，生成訓練矩陣E。本文的模型訓練次數為10，每次訓練可有多次迭代，若某次訓練從E中隨機抽取a行樣本組成樣本矩陣Es，則每次訓練可迭代d/a次。設棧式自編碼器的層數為3，每層均為1個自編碼器，每個自編碼器均包含1個編碼器和1個解碼器，每個自編碼器的學習率r設定為0.01，選取不同的Es輸入式(1)中生成編碼器，再將編碼器輸入解碼器中，利用式(2)還原矩陣Er，并通過式(3)計算從編碼輸入到解碼輸出間的損失，采用式(7)進行模型優化。提取第10次訓練第3層AE的隱藏層M，并保存同批次的各層權值矩陣Ge與偏置矩陣Be，作為水印檢測時的模型參數。6)零水印生成：由于各次訓練選取訓練樣本數量設定為a，根據棧式自編碼器的運算性質，得到的矩陣M大小為p×p，即與水印序列矩陣WM大小一致。M中各元素均為實數，且mi,j∈[0,1]，按式(8)將M轉換成特征矩陣Mf，并與矩陣WM按位進行異或操作，生成零水印圖像Wzero(式(9))。7)將Wzero提交至IPR( Intellectual Property Rights )注冊中心，用于后續版權驗證。

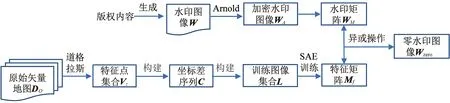
圖3 零水印構建流程Fig.3 Construction process of zero-watermarking

(4)

(5)

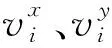
(6)

式中：“?”為補位符，即在原序列C末尾，按條件補上若干個或者若干位C序列，補位后d≥3d2。

optimizer(r,cost)=AdamOptimizer(r).minimize(cost)

(7)

式中：r為學習率；minimize表示最大限度地最小化；cost為模型定義的代價函數。式(7)為TensorFlow的內嵌函數，引入二次方梯度校正，用于尋找全局最優點的優化算法。

(8)

Wzero=Mf⊕WM

(9)

2.2 水印檢測

采用相同的閾值τ對待檢測矢量地圖進行道格拉斯—普克壓縮，提取特征點集V′1；構建V′1的坐標差序列C′并轉換成二值圖像集L′；調取構建零水印時保存的各層權值矩陣Ge和偏置矩陣Be，作為自編碼器模型的參數，將L′輸入訓練好的自編碼器中，構建相同的訓練矩陣E′和E′s，獲得矩陣M′(m′i,j為M′中元素)，利用式(10)生成待檢測數據的特征矩陣M′f。

(10)

從IPR注冊中心獲取零水印圖像Wzero，將其矩陣化后，與M′f進行異或操作，得到1個加密水印圖像W′A(式(11))，對W′A進行Arnold逆置亂后得到待檢測數據的水印圖像W′，計算W與W′之間的NC值(式(12))[21]，若NC值大于設定的閾值，則認為驗證成功，否則不能判定待檢測數據的版權所屬。同時，采用比特誤差率BER(Bit Error Ratio)[4](式(13))定量驗證提取的水印信息誤差。

W′A=M′f⊕Wzero

(11)

(12)

式中：Wi,j與W′i,j分別為原始水印圖像與還原的水印圖像在第(i,j)位的水印信息；NC值范圍為0～1。

(13)

式中：N為水印信息的長度。

3 實驗與分析

3.1 實驗數據及預處理

本文選擇道路矢量和建筑物矢量作為實驗數據(圖4)，數據的基本信息與預處理后信息如表1所示，兩組數據設置的壓縮閾值均為10 m，壓縮比分別達到85.65%和69.33%。圖5為待嵌入的二值水印圖像以及進行Arnold置亂加密的過程，水印圖像中含有意義的版權內容“地理學院”，大小為60×60像素。在Arnold置亂公式中所有參數均取1的情況下，可得本文實驗圖像的置亂周期為120次，即在第120次時恢復為原始狀態。為提升安全性，本文選用第80次置亂時的水印圖像用于零水印構建。在還原水印圖像時，本文設定NC閾值為0.8，當NC大于0.8時，認為版權認證成功，否則認證失敗。

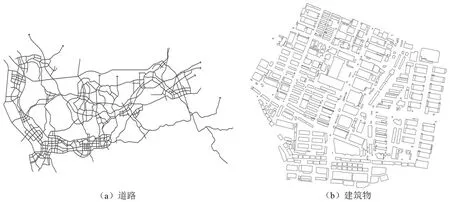
圖4 原始實驗數據Fig.4 Original experimental data

表1 實驗數據的基本信息Table 1 Basic information of the experimental data

圖5 水印圖像置亂加密Fig.5 Scrambling encryption of watermark image

3.2 抗幾何攻擊分析

常見的幾何攻擊主要包括平移、旋轉和縮放3種方式，因此，水印算法能否抵抗幾何攻擊是檢驗魯棒性的重要指標。實驗進行了3次不同強度的平移、旋轉和縮放攻擊，在此基礎上還原水印圖像，并進行對比驗證(表2)。可以看出，在不同強度的幾何攻擊下，兩組數據均可還原出高質量的水印圖像，版權內容清晰可見；NC值均不低于0.98，遠大于設定的閾值，BER值也僅為3%左右，表明本文提出的零水印算法展現了良好的抗幾何攻擊能力。但也發現，還原水印圖像的NC值均未達到1，因為在幾何攻擊下，坐標值發生了變化，導致自編碼器在特征提取過程中發生偏移，但偏移程度不會影響水印功能的正常實現，同樣展現了自編碼器強大的特征提取能力。

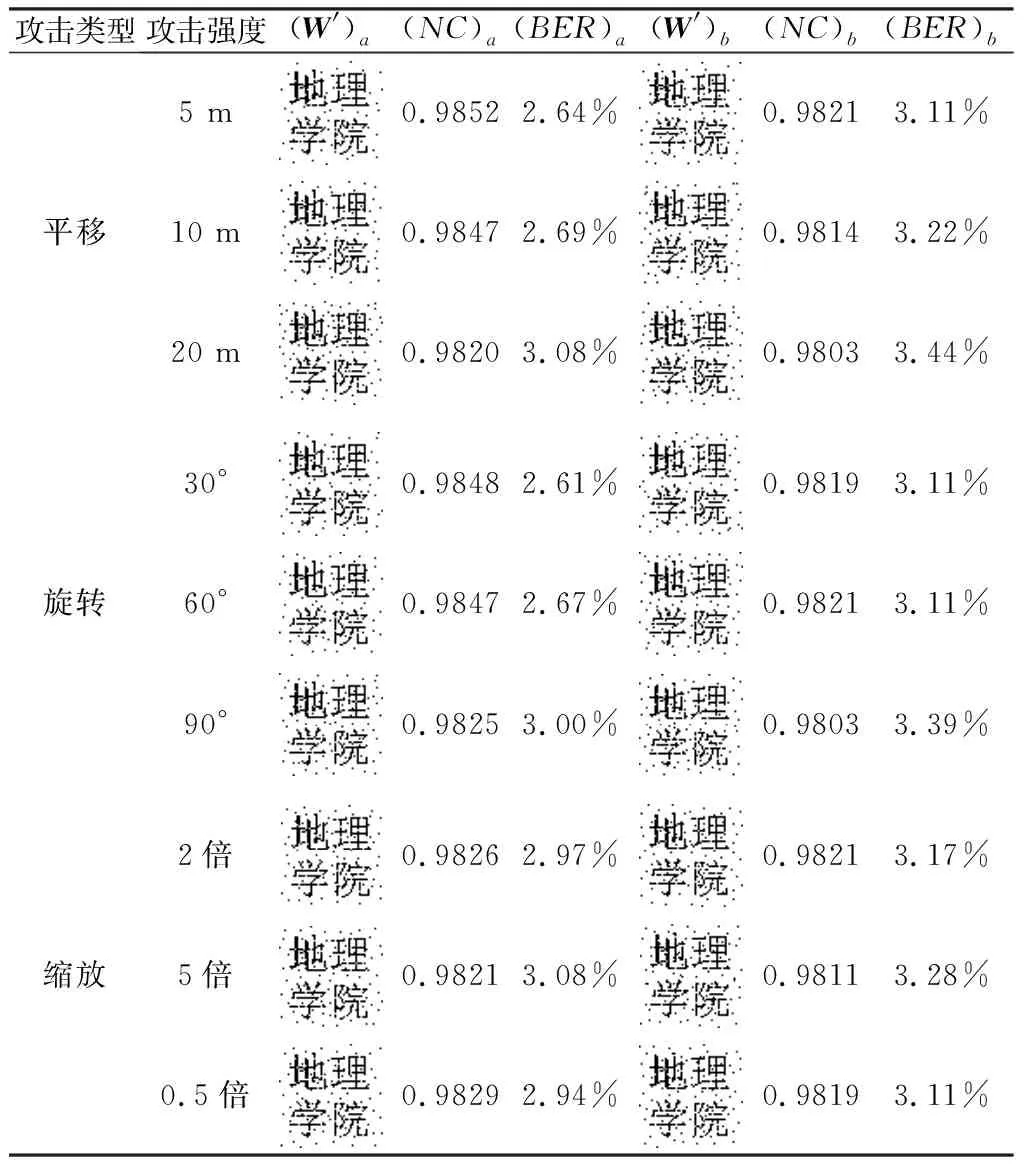
表2 幾何攻擊結果Table 2 Results of geometric attacks

3.3 抗坐標點攻擊分析

坐標點攻擊主要包括隨機增點、隨機刪點和壓縮3種攻擊方式，不同攻擊類型同樣設定3次不同的攻擊強度，攻擊結果如表3所示。在隨機增點和隨機刪點的實驗中，均可提取出NC值大于0.98的高質量水印圖像，成功驗證版權；且隨著攻擊強度增點，提取結果出現輕微下滑趨勢。因此，本文提出的零水印算法對隨機增點和隨機刪點的魯棒性很強。在壓縮攻擊下，本文兩組實驗數據的壓縮比閾值分別為85.65%和69.33%，當壓縮閾值不超過本文預設的閾值時，即壓縮比小于特征點提取閾值時，可以提取出NC為1的完整水印圖像。因此，當輸入值相同，本文的自編碼器水印算法可提取出相同的特征信息。在建筑物數據中，壓縮比為75%，超過預設的壓縮閾值時，可提取出的水印圖像NC值為0.9749，仍能有效完成版權驗證。綜上所述，本文提出的零水印算法對坐標點攻擊具有較強的魯棒性。

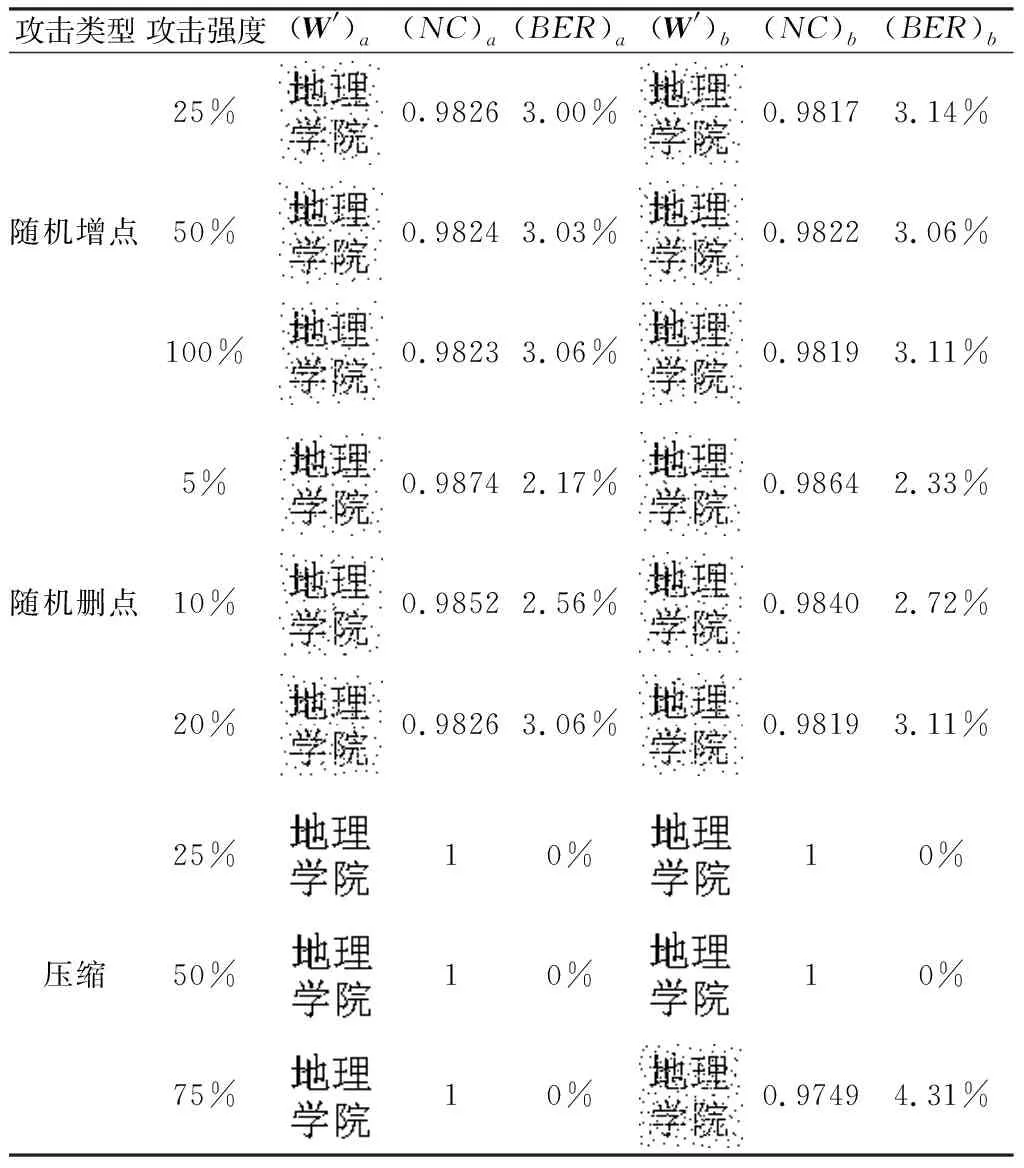
表3 坐標點攻擊結果Table 3 Results of vertex attacks

3.4 唯一性檢驗

為檢驗零水印的唯一性，將兩組實驗數據得到的零水印圖像進行交叉提取，并將提取結果與原始水印圖像進行相似性檢驗(表4)。可以看出，交叉提取得到的水印圖像NC值分別為0.5049和0.5128，無法識別出有效水印信息，表明不同數據基于本文算法生成的零水印圖像無法提取、還原其他數據生成的水印信息，算法具有唯一性。

表4 唯一性檢驗結果(NC值)Table 4 Results of uniqueness test (NC value)

3.5 算法對比分析

本文選取前人研究中兩組魯棒性較強、可抵御多種水印攻擊的零水印算法[13,14]，與本文提出的零水印算法進行魯棒性對比(表5，“√”表示可成功驗證版權，“×”表示無法驗證版權)。從表5可以看出，相較對比水印算法，本文算法在對抗常見的幾何攻擊、坐標點攻擊時，顯示出更強、更全面的魯棒性，但對抵抗裁剪攻擊的能力較差。

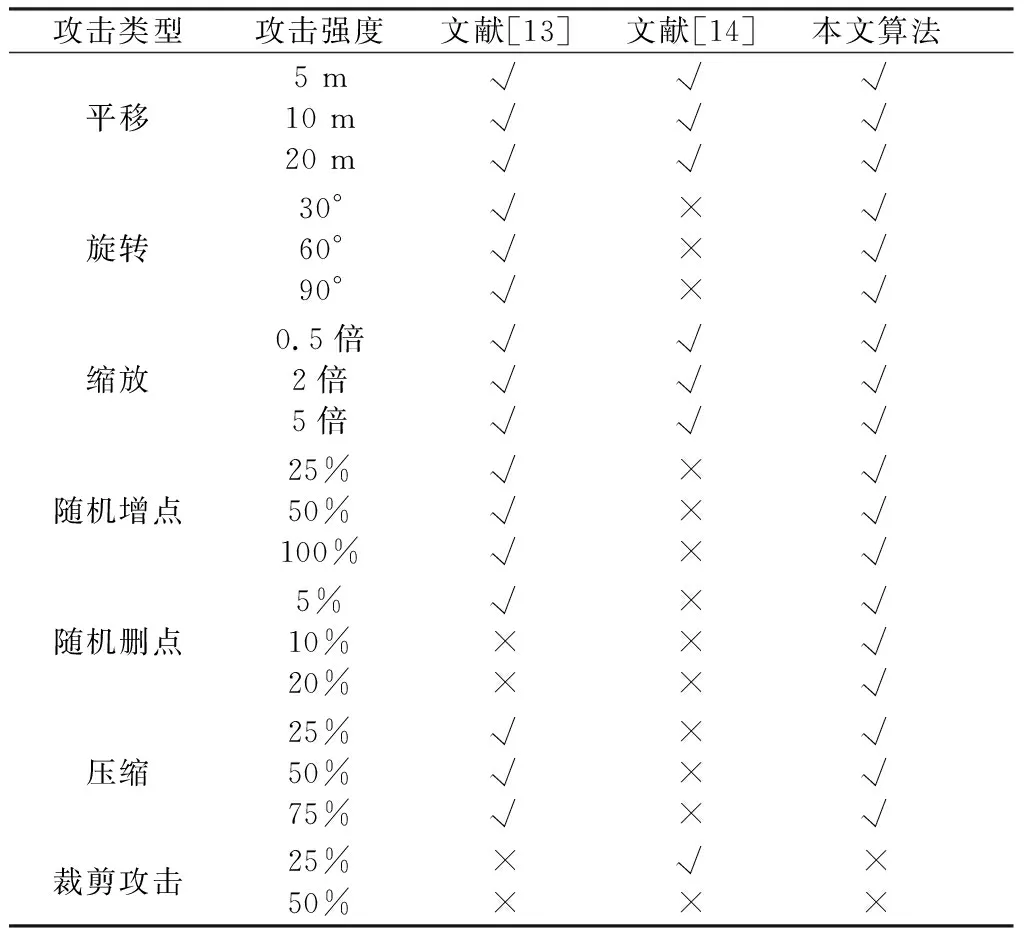
表5 對比實驗結果Table 5 Results of contrast experiments

4 結論

本文引入深度學習中的棧式自編碼器模型構建零水印算法，因其能有效提取數據深層、穩定的特征，進行相應的改造后可應用于提取矢量地理數據中的特征信息，實驗證明,利用棧式自編碼器特征信息構建的零水印算法對幾何攻擊、坐標點攻擊、數據壓縮攻擊等具有較強魯棒性，可為矢量地圖版權保護提供技術參考。但本文算法抵抗裁剪攻擊的能力較差，且在構建訓練圖像集方面，是否還有比坐標差序列更合適的方法，有待進一步研究。