2013-2020年京津冀地區PM2.5濃度時空變化模擬及趨勢分析

楊 曉 輝，肖 登 攀,*，柏 會 子，唐 建 昭，王 衛，郭 風 華，劉 劍 鋒

(1.河北省科學院地理科學研究所/河北省地理信息開發應用技術創新中心，河北 石家莊 050011；2.河北師范大學地理科學學院，河北 石家莊 050024；3.河北省環境演變與生態建設實驗室，河北 石家莊 050024)

0 引言

PM2.5(空氣動力學粒徑<2.5 μm的細顆粒物)可以攜帶有毒有害物質[1]，長期暴露在PM2.5下會對人類健康產生不良影響[2,3]。中國快速的城市化和工業化導致PM2.5成為空氣污染的主導因素[4]，全面了解PM2.5的空間分布具有重要意義[5]。然而，由于地面監測站點數量稀疏，可獲得的監測數據有限，嚴重阻礙PM2.5的相關研究[6,7]。衛星遙感可為地面PM2.5污染監測提供有價值的信息，特別是對于無PM2.5監測站點的地區[8,9],衛星反演的氣溶膠光學厚度(AOD)與PM2.5濃度高度相關[8,10,11]，高空間分辨率的AOD產品能以更精細的尺度對PM2.5濃度進行更精確的評估[12-14]。2018年美國國家航空航天局(NASA)基于多角度大氣校正(MAIAC)算法[15]生成1 km高空間分辨率AOD產品(MCD19A2)，在預測PM2.5濃度方面顯現出優越性能[16-18]。近年來，許多學者通過比例因子法、半經驗公式和統計回歸模型等探索PM2.5濃度和衛星AOD數據之間的定量關系，其中，統計回歸模型以快速、簡單和準確等特點得到廣泛應用。從早期研究的簡單線性回歸[10]到先進的高級統計模型，如線性混合效應(LME)模型[19]、廣義加和(GAM)模型[20]、地理加權回歸(GWR)模型[21]、時空線性混合效應(STLME)模型[22,23]和地理時間加權回歸(GTWR)模型[24]等，之后通過組合兩個模型(如LME+GWR、LME+GAM和TEFR+GWR等)[25-27]或三階段統計模型(如IPW+GAMM+KED)[28]減少單一模型預測帶來的偏差[29]。此外，部分學者雖然使用隨機森林(RF)模型[30]、自適應深度神經網絡(SADNN)模型[6]和支持向量機(SVM)[31]等機器學習模型預測PM2.5濃度，但不能給出特定的模型參數以解釋PM2.5-AOD的時空關系。

研究表明，在模型中添加交互項(AOD的二次項)可以更好地描述非線性效應[32]，在PM2.5污染較嚴重區域能糾正PM2.5濃度預測偏差[32，33]。因此，本研究選擇LME+GWR兩階段統計回歸模型以精確捕捉PM2.5-AOD的時空變化，以MAIAC AOD為主要變量，氣象和土地利用因子為輔助變量，預測每日地面PM2.5濃度，同時模型中加入AOD的二次項以及行星邊界層高度(PBLH)和AOD的交互項，以解釋PM2.5-AOD的非線性關系，并使用十折交叉驗證評估模型預測的準確性，最后利用模型建立長時間序列高空間分辨率的PM2.5濃度數據集，分析PM2.5地基監測網絡建立以來京津冀地區2013―2020年PM2.5濃度時空變化趨勢，以期為京津冀地區大氣污染防治工作提供參考和建議。

1 研究區與數據

1.1 研究區概況

京津冀地區是我國北方重要的行政、經濟和文化中心，包括北京市、天津市和河北省的11個地級市(圖1)，該地區人口稠密，以煤炭為主要能源的第二產業排放各種大氣污染物，尤其在內陸平原地區，大氣污染物難以擴散，空氣污染嚴重。2013―2020年《中國環境公報》(http://www.cnemc.cn/jcbg/zghjzkgb/)指出：中國空氣質量較差的10個城市中，京津冀地區歷年分別占7、8、7、6、6、5、4和1個。雖然近年來該地區空氣質量有所改善，但仍需重視PM2.5濃度的時空分布特征和變化趨勢研究。

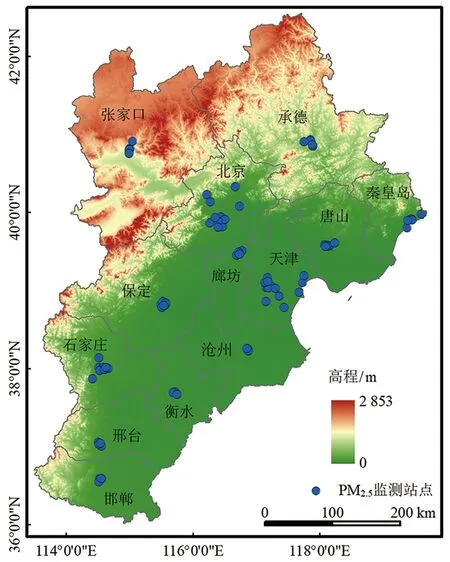
圖1 研究區PM2.5監測站點分布Fig.1 Study area with PM2.5 monitoring stations

1.2 數據來源和處理

基于AOD的PM2.5濃度預測模型加入氣象和土地利用等因子，可顯著提高模型預測精度[22,34]。本研究采用LME+GWR兩階段統計回歸模型，除主要預測因子AOD外，其他輔助預測因子包括行星邊界層高度(PBLH)、近地面溫度(TEMP)、近地面風速(WS)、近地面相對濕度(RH)、近地面氣壓(PRS)、降水量(PRCP)、森林覆蓋率(FC)和建筑用地覆蓋率(UC)，通過預測變量選擇和多重共線性分析篩選得以利用。數據集涵蓋時間為2013年1月1日至2020年12月31日，詳細信息見表1。

表1 數據來源與時空分辨率Table 1 Data source and spatial-temporal resolution

(1)PM2.5監測數據。京津冀80個監測站點PM2.5濃度的小時尺度數據均來自全國城市空氣質量實時發布平臺。為確保PM2.5數據有效性，在日均PM2.5濃度擬合過程中，剔除不在國家環境空氣質量標準(NAAQS)[35]監測范圍內的數值(即PM2.5濃度<2 μg/m3或PM2.5濃度>500 μg/m3)。

(2)MAIAC AOD數據。MAIAC算法在反演過程中利用時間序列分析和空間分析增強了對比局部尺度氣溶膠變化的能力，提高了云雪檢測和氣溶膠反演的質量[36]。從NASA獲得MODIS C6 MAIAC Terra/Aqua AOD(0.55 μm)產品，利用氣溶膠地基觀測網(http://aeronet.gsfc.nasa.gov/)中Beijing、Beijing-CAMS和Xianghe的 AERONET AOD 數據(版本 3，級別 2)的驗證結果(圖2)表明，決定系數R2為0.81～0.91，均方根預測誤差RMSPE為0.10～0.25 μg/m3，73.15%～83.74%的樣本落在期望誤差區間(±(0.05+20%×AERONET AOD))內，滿足驗證精度要求。

(3)氣象數據。2013-2020年PBLH數據來源于GEOS5-FP的網格化數據產品；2013-2018年其余氣象數據(TEMP、WS、RH、PRS和PRCP)來源于國家青藏高原數據中心[37]，由于數據集只涵蓋1979-2018年，從中國氣象數據網下載分辨率相近的2019-2020年的氣象數據。

(4)土地利用數據。土地利用數據來源于地理國情監測云平臺，本研究選取2015年土地利用數據代表2013-2020年的土地利用狀況，提取計算整個研究區建筑用地覆蓋率和森林覆蓋率加入模型。

為使各類數據的時空分辨率與每日PM2.5濃度相匹配，日均PBLH數據由MODIS衛星過境期間兩次觀測均值獲得；所有日均氣象變量使用雙線性內插法重新采樣到與MAIAC AOD相同空間范圍(1 km×1 km)；森林和建筑用地覆蓋率在以每個PM2.5監測站點為中心的1 km×1 km緩沖區內進行平均。將上述MAIAC AOD、氣象和土地利用變量按經緯度提取到80個監測站點，并根據站點和日期將提取結果與PM2.5濃度數據進行匹配，最后，刪除MAIAC AOD和PM2.5的非隨機缺失數據，2013-2020年分別獲得13 272(300 d)、15 413(325 d)、15 657(316 d)、21 882(330 d)、16 961(323 d)、10 942(300 d)、10 987(281 d)和11 698(299 d)條數據記錄。

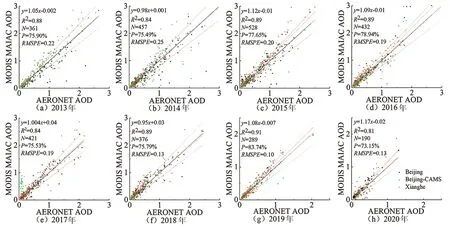
注：紅色虛線是回歸線,黑線是1∶1 線,灰線代表期望誤差區間。

2 研究方法

2.1 共線性診斷

為提高預測模型的穩定性，必須考慮自變量的共線性。本研究選擇方差膨脹因子(VIF)(式(1))和容差(TV)(式(2))診斷所選變量之間的共線性[38]。VIF越大，說明自變量之間存在共線性的可能性越大，當自變量的TV>0.1且VIF<10時，表明自變量之間無共線性問題存在。由表2可知，參與模型的所有自變量每年的VIF和TV均滿足VIF< 10和TV> 0.1的條件，表明自變量之間不存在共線性問題，均可考慮用于模型擬合。

表2 變量共線性分析中方差膨脹因子(VIF)和容差(TV)范圍Table 2 Range of variance inflation factor (VIF) and tolerance value (TV) in the analysis of variable collinearity

(1)

(2)

式中：Ri為自變量Xi對其余自變量作回歸分析的負相關系數。

2.2 標準差橢圓(SDE)

標準差橢圓(SDE)是基于一組離散點的平均中心概括地理要素(本文為PM2.5濃度)空間特征(集中趨勢、離散度和方向趨勢)[39]的方法，輸出參數包括標準差橢圓、平均中心、長短軸和方位角[40]。其中，標準差橢圓表示要素空間分布的主體區域，其變化可以描述整個空間動態過程的特征；平均中心的移動可揭示要素的整體演化軌跡；橢圓長軸和短軸的變化表示特定空間方向的擴展或收縮；方位角的變化表示整體要素在特定空間方向上的變化[41]。

2.3 模型構建與驗證

本研究采用由線性混合效應(LME)模型和地理加權回歸(GWR)模型組成的兩階段統計回歸模型對PM2.5-AOD關系的時空變化進行模擬，第一階段LME模型用以校正PM2.5-AOD的時間變化關系，模型中添加了AOD的二次項以及AOD和PBLH之間的相互作用，以解釋 AOD和PM2.5之間的非線性關系。計算公式為：

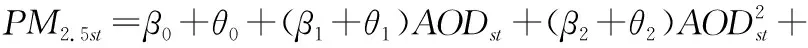
(3)

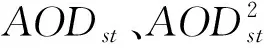
第二階段GWR模型用以校正PM2.5-AOD的空間異質性，通過對LME模型的殘差進行建模，每天擬合一次以說明時間可變性，具體計算公式為：

PM2.5_resist=β0(us,vs)+β1(us,vs)AODst+εst

(4)

式中：PM2.5_resist為LME模型中地面監測站點s第t天的殘差值；AODst為監測站點s第t天的MAIAC AOD值；β0(us,vs)和β1(us,vs)分別為空間坐標為(us,vs)監測站點s處的回歸截距和回歸斜率。

本文采用十折交叉驗證[29]檢測模型的過擬合程度，首先，整個模型擬合數據集被隨機分成10個子集，每個子集包含大約10%的數據集，在每次交叉驗證中選擇一個子集作為測試樣本，并使用剩余的9個子集擬合模型以對測試樣本進行預測，此過程重復10次以確保所有子集都被預測。此外，對實測和預測的PM2.5濃度進行線性回歸擬合，利用擬合后R2、斜率、RMSPE和相對預測誤差(RPE)評估模型性能。計算公式為：

(5)

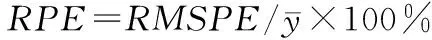
(6)

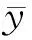
3 結果與分析

3.1 統計分析

京津冀地區地面監測站點觀測PM2.5年均濃度范圍為40.97～91.27 μg/m3，2013年最高，2020年最低，表明過去8年間PM2.5污染程度呈下降趨勢，但仍超過國家環境空氣質量二級標準(GB3095-2012)的限值(35 μg/m3)。同期年平均AOD范圍為0.37～0.69，森林和建筑用地年均覆蓋率分別為3%～5%和55%～78%，2013―2020年各氣象變量的范圍見表3。

表3 建模變量統計指標Table 3 Statistical indicators of modeling variables

3.2 模型擬合與驗證

2013-2020年LME+GWR模型擬合和交叉驗證結果對比(圖3)顯示，在捕捉每日PM2.5濃度方面，模型表現性能優異。模型擬合時，數據分布向回歸線集中，模型擬合R2范圍為0.89～0.97，表明兩階段模型可以解釋地面89%～97%的PM2.5濃度變化；斜率為0.89～1.04，表明模型的預測偏差較小，能較好地克服高值低估問題；RMSPE和RPE分別為6.85～24.60 μg/m3和16.67%～26.95%。與模型擬合相比，交叉驗證后模型R2為0.85～0.95，RMSPE為7.87～29.90 μg/m3，RPE為19.19%～32.72%，可以看出，交叉驗證后模型R2減小，而RMSPE和RPE增加，表明模型存在輕微的過度擬合。

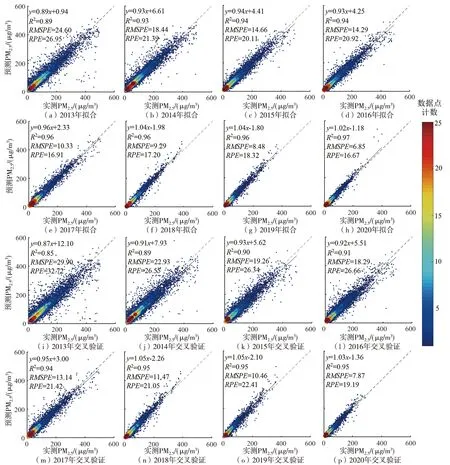
圖3 2013-2020年模型擬合和交叉驗證結果對比Fig.3 Comparison of model fitting and cross-validation results from 2013 to 2020

不同年份中，2020年模型性能最好，交叉驗證后模型R2最高，為0.95，RMSPE和RPE值最小，分別為7.87 μg/m3和19.19%，這主要是由于隨著政府對“大氣污染防治行動計劃”的開展，PM2.5濃度出現下降。2020年大約93.72%的數據樣本PM2.5濃度小于100 μg/m3。相比之下，2013年模型性能最差，交叉驗證后模型R2最低，預測不確定性最大，主要原因是超過32.38%的數據樣本PM2.5濃度大于100 μg/m3，相對離散的數據樣本可能增加了模型擬合的難度。綜上，LME+GWR模型穩健，使用1 km MAIAC AOD產品結合LME+GWR模型在京津冀地區可以很好地模擬每日地面PM2.5濃度。

3.3 京津冀地區PM2.5濃度時空分布

基于標準差橢圓分析2013-2020年京津冀地區PM2.5濃度空間格局的逐年變化(圖4)，可以看出，PM2.5主要集中在京津冀平原區，說明在整個研究期內，京津冀平原區是全域PM2.5總量的主要貢獻者。PM2.5濃度重心逐漸向東北方向移動，仍處于滄州市內。橢圓長軸從2013年的242.17 km減至2017年的239.03 km，表明該時段京津冀地區PM2.5年均濃度在主要方向上呈現空間集聚趨勢，但集聚程度不大，之后又輕微增至2020年的242.18 km，表明該時段PM2.5濃度在主要方向上出現分散趨勢；短軸從2013年的101.40 km增至2020年的105.11 km，表明京津冀地區PM2.5在地理空間上呈擴張分散化趨勢；從方位角變化范圍看，PM2.5濃度總體呈“西南—東北”方向空間分布格局，該地理空間走向與京津冀地形密切相關；轉角由2013年的40.53°波動縮小至2020年的39.56°，表明PM2.5空間分布格局存在沿西北方向微弱偏移趨勢。

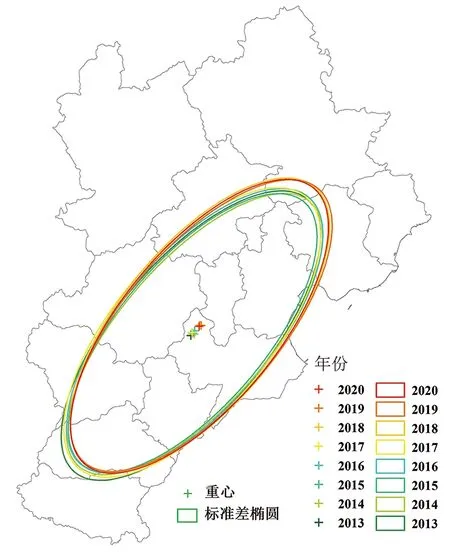
圖4 2013-2020年PM2.5濃度重心和標準差橢圓的空間變化Fig.4 Spatial changes of PM2.5 concentrations gravity center and standard deviational ellipse from 2013 to 2020

基于兩階段統計回歸模型預測的2013-2020年京津冀地區PM2.5年均濃度分布狀況(圖5)可知，PM2.5濃度空間分布趨勢大致相同，南北差異顯著。PM2.5濃度低值區位于西部和北部山區，高值區位于平原，與標準差橢圓分析結果一致。總體而言，PM2.5濃度呈現出“北部山區低，南部平原高(平原西南高濃度、東北中等濃度)”的空間分布格局。2013-2020年京津冀地區PM2.5年均濃度分別為69.67、65.31、49.26、51.17、44.96、43.11、34.54和32.02 μg/m3，可以看出，2013-2014年PM2.5年均濃度波動較小，2015年出現大幅下降，2017年PM2.5年均濃度下降35.47%，達到“大氣污染防治行動計劃”中“到2017年下降25%”的要求，主要原因在于2017年是《大氣十條》實施效果的驗收年，政府防治力度加大[42]。此外，2019年PM2.5年均濃度下降更明顯，2020年下降54.04%，相對2017年下降28.78%，PM2.5污染程度總體下降顯著。從區域看，高濃度區明顯縮小，污染城市主要集中在邯鄲、邢臺、石家莊、保定和衡水。2013年高濃度區范圍最大，2017-2020年低濃度區域逐漸擴大，2019和2020年京津冀全域PM2.5濃度降至55 μg/m3以下。

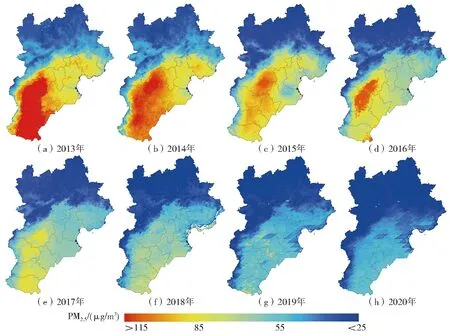
圖5 2013-2020年PM2.5年均濃度空間分布Fig.5 Spatial distribution of annual mean PM2.5 concentrations from 2013 to 2020

京津冀地區PM2.5污染也表現出較強的季節性變化。整體看，PM2.5濃度呈現“冬季高，夏季低，春秋過渡”的季節變化特點(圖6)。2013年和2014年全年PM2.5濃度較高，冀中南地區春季PM2.5濃度大于85 μg/m3，冬季大于115 μg/m3；2015-2020年京津冀地區PM2.5濃度逐漸降低，夏季均小于55 μg/m3，2019-2020年甚至低于30 μg/m3；2013-2018年秋季、冬季和春季污染范圍逐漸縮小，污染嚴重地區主要集中在邯鄲、邢臺、保定和石家莊等市；2019-2020年春夏秋三季均小于55 μg/m3。2013-2020年冬季PM2.5濃度均值依次為117.46 μg/m3、84.24 μg/m3、75.30 μg/m3、72.72 μg/m3、55.97 μg/m3、44.63 μg/m3、51.48 μg/m3和51.42 μg/m3，逐年下降并在2017年后趨于穩定，2018-2020年冬季重污染區范圍顯著減小，輕污染區范圍擴大，導致相對2017年PM2.5濃度變化不大；2017年和2020年相比2013年冬季PM2.5濃度分別下降了61 μg/m3(52%)和66 μg/m3(56%)。

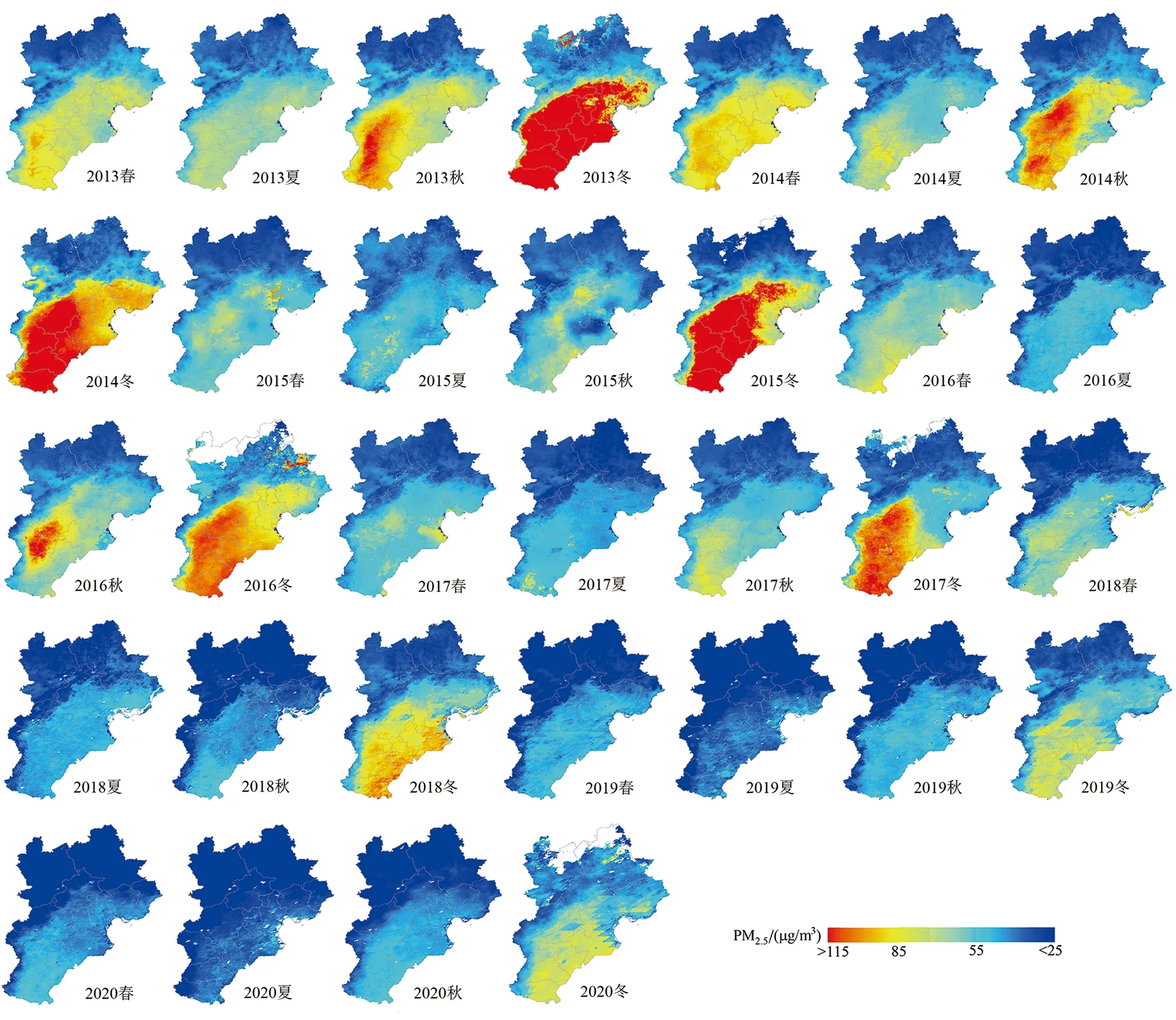
圖6 2013-2020年PM2.5季均濃度空間分布Fig.6 Spatial distribution of seasonal mean PM2.5 concentrations from 2013 to 2020

為了解京津冀地區各市域之間的差異，利用預測結果計算各城市PM2.5年均濃度(圖7)。2013-2020年承德和張家口PM2.5濃度較低，8年內均低于35 μg/m3；邯鄲、邢臺和衡水PM2.5濃度居前三位，2013年PM2.5濃度均超過100 μg/m3，到2020年PM2.5濃度分別降為47.17 μg/m3、47.28 μg/m3和50.05 μg/m3，與滄州和廊坊接近。此外，2013-2017年北京PM2.5污染在13個城市中排名第10位，2018年之后降至第11位，屬中低污染水平，可能緣于重污染行業的搬遷。

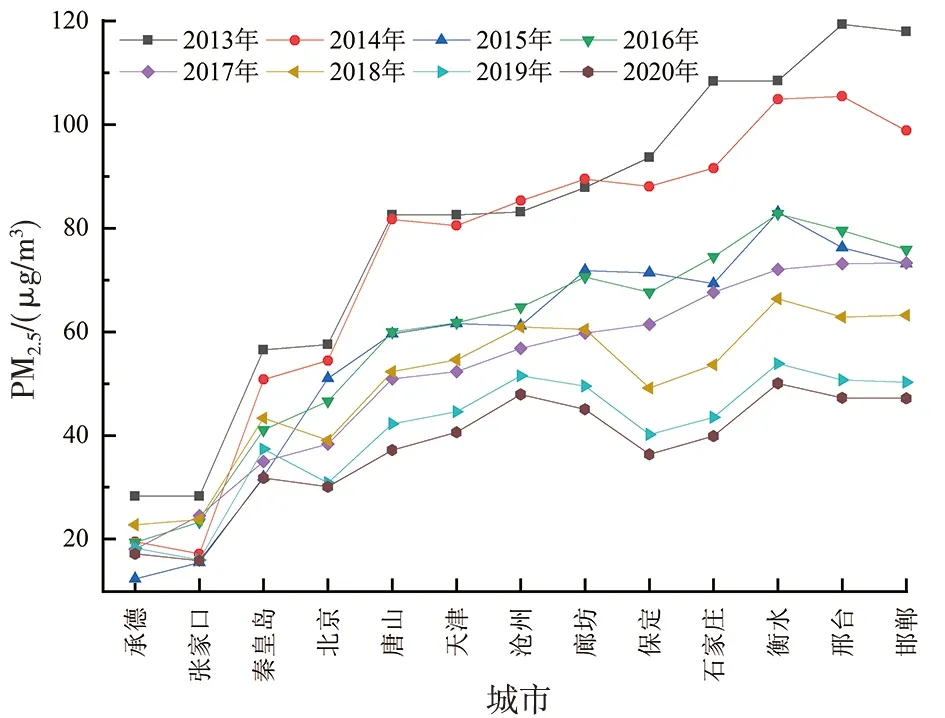
圖7 2013-2020年各城市PM2.5年均濃度Fig.7 Annual mean PM2.5 concentrations in each city from 2013 to 2020

4 結論與討論

本文基于京津冀地區2013-2020年的日均PM2.5濃度數據，結合MAIAC AOD、氣象和土地利用等因子，利用兩階段統計回歸模型模擬京津冀地區每日PM2.5濃度的時空分布，其中第一階段采用LME模型反映PM2.5-AOD關系隨時間變化規律，第二階段加入GWR模型反映PM2.5-AOD關系的空間變異，主要研究結論如下：1)十折交叉驗證結果表明LME+GWR模型穩健，使用1 km MAIAC AOD產品結合LME+GWR模型對京津冀地區PM2.5-AOD之間的時空變化模擬性能優異；2)PM2.5濃度總體呈現出“西南—東北”方向空間分布格局，且存在沿西北方向微弱偏移趨勢；PM2.5濃度的重心向東北輕微移動，結合橢圓的長、短半軸可知，京津冀PM2.5濃度呈現輕微擴張分散化趨勢；3)由LME+GWR模型模擬得到的京津冀地區2013-2020年地面PM2.5濃度整體呈現“南部平原高、北部山區低”和“冬高夏低、春秋過渡”的時空特征，2018-2020年冬季低污染區域有擴大趨勢，需格外重視。

與已有研究相比，本研究構建的模型(LME+GWR)性能良好。對于低空間分辨率(3～10 km)的 PM2.5模擬研究[26,43,44]，該模型具有更高的R2和更低的RMSPE；與使用高空間分辨率(1 km)AOD預測PM2.5濃度的模型[12,45]性能相似。盡管本研究使用了Terra和Aqua融合后的MAIAC AOD數據，但仍沒有達到區域內全覆蓋。AOD數據缺失會對模型預測精度產生一定影響，主要表現為“高值低估”[37]，這是后續研究的方向之一。如Chen等[46]開發了混合效應模型和逆距離加權(IDW)兩步插值技術填補AOD缺失值，整體上AOD缺失率從87.91%(Auqa)和85.47%(Terra)降低至融合后的13.83%且R2達0.76。 此外，未來可以在更大的研究區域內考慮更多相關時空因素，以擴大研究區域并提高模型模擬精度。