“十”字形自驅單元形成寡聚體的動力學行為*

何景熙 秦超然 許天亮 陳康? 田文得?

1) (蘇州大學軟凝聚態物理及交叉研究中心,蘇州 215006)

2) (蘇州大學物理科學及技術學院,蘇州 215006)

1 引言

自組裝是自然界創造物質的主要手段.組裝是一個系統從無序變成有序的過程,可以發生在不同的時間和空間尺度.分子尺度自組裝的一個重要特點是需要分子間弱吸引相互作用[1?9],組裝基元在弱吸引作用下自發聚集形成穩定的結構,比如病毒外殼[10]、細胞雙層磷脂膜結構[10]等.熱運動是促使微觀尺度(甚至介觀尺度,比如膠體體系)的分子通過擴散運動在空間中尋找到其他分子的主要動力;這類組裝過程一般不需要消耗外部能量.隨著尺度的增大,熱運動效應逐漸可以忽略,比如顆粒物質體系[11,12];這類系統的組裝需要不斷外部能量的輸入,一個典型的例子是沙丘的形成需要風力的驅動.

近幾年,隨著活性物質系統研究的爆發性增長,科研工作者開始關注自驅動力作用下,系統的組裝行為.這類系統由自驅動的單元組成,比如,人類群體、動物群體、活細胞和組織、活性膠體和合成的微型馬達.自驅單元具有從周圍環境中汲取能量并轉換為運動的能力.活性物質系統代表了統計物理中一個全新的非平衡狀態.傳統非平衡系統的定向驅動力來源于熱力學變量或邊界條件(如溫度和壓力)的全局變化,而活性物質系統在單粒子水平上是不平衡的.這一獨特的非平衡驅動力與系統固有的隨機性結合導致活性物質呈現豐富的集體行為[13?19].自驅單元的形狀會顯著地影響其組成結構以及組裝之后團簇的性質,如圓形的自驅單元會形成有缺陷的緊密六方堆積的團簇[14?16],團簇周邊的粒子會不停地進行更迭,形成一個類似液態的相.方形粒子會形成有缺陷的四方堆積團簇[18],與圓形粒子相比,團簇與外界沒有粒子交換,形成的相更接近于固態,且方形粒子在團簇中不能輕易改變方向,因此會產生力矩使團簇進行旋轉.橢圓形粒子會隨著自身橫縱比的改變而產生不同的現象[14],當橫縱比接近1 時,橢圓形粒子因對稱性破缺不會像圓形粒子那樣產生大團簇,反而會分布在整個空間中;當橫縱比遠離1 時,粒子取向的趨同性將越來越明顯,由此產生極性向列帶.棒狀粒子根據橫縱比的不同也會有不同的現象[13]:短棒形成小團簇;當短棒變長時,團簇會變大并且產生渦旋;長棒會產生跨區域的條帶狀團簇.圓錐形粒子會根據自推進力方向不同而有不同的現象[17],當自推進力朝大頭時,會產生若干個小團簇,而當自推進力朝小頭時,會產生大規模的向列集群.

一個重要的挑戰是理解形狀對活性物質體系自組裝行為的影響.一方面形狀會導致相互作用的各向異性,另一方面形狀也影響組裝體的動力學行為.本文設計了一種對稱性較低的“十”字形粒子.從對稱性上來看,圓形粒子有著最高的對稱性;其次是方形粒子,有著四重對稱性;棒狀粒子和橢圓形粒子有著二重對稱性,圓錐形粒子僅有著一重對稱性.“十”字形粒子與方形粒子一樣有著四重對稱性,但不同的是,“十”字形粒子是一種邊緣對稱向中間凹陷的粒子.在目前的研究中,很少有描述關于這種邊緣對稱向中心凹陷粒子的.但在實際應用中,這種形狀是十分常見的,一個典型的例子就是齒輪,通過其伸長的臂與其他物件相互作用.在實驗中發現,與其他形狀的粒子不同,“十”字形粒子可以依靠空間位阻效應與自驅動力協調而自發產生許多構型各異的寡聚體,一部分寡聚體十分穩定,在沒有外力的干擾下,至實驗結束,它們都維持著自身的運動并且其結構都沒有產生變化.研究它們寡聚體(二聚體、三聚體、四聚體)的動力學,是理解此類形狀大量粒子組裝的第一步.“十”字形粒子與圓形、橢圓、方塊粒子相比,由于其有四個臂,其空間位阻效應具有很好的各向異性,同時旋轉時對周圍的粒子也能產生較穩定的扭矩.相對于微觀尺度需要吸引作用,本文強調空間位阻和自驅動力協同效應導致的聚集行為.發現這些構型的行為模式按照幾何中心軌跡可大致分為兩類:第一類是平動與轉動相結合的運動模式,幾何中心繞著小圈進行無規則擴散,這一類在構型自驅動力合力為零的情況下出現;第二類是做圓周半徑較大的偏心旋轉,這一類在構型自驅動力合力不為零的情況下出現.本文第2 節介紹了實驗場地與“十”字形粒子的制作,第3 節介紹不同的寡聚體的運動行為,最后進行總結.

2 實驗設計和軌跡分析

如圖1 所示,采用hexbug 馬達[20]作為活性粒子進行實驗,hexbug 的尺寸為45 mm×14 mm×17 mm,通過7 號電池供電(圖1(a)).hexbug 內置了一個不對稱的旋轉馬達,通過馬達產生振動,底部的12 條不對稱軟腿會在幾個振蕩周期之后進行定向運動.用PVC 發泡板切割出“十”字形結構(圖1(b)),尺寸為6 cm×6 cm×1 cm,每條邊2 cm,在四條臂底部扎入針,防止實驗中粒子翻倒.為了追蹤粒子,在它們上面貼上了識別卡片,卡片幾何中心有一個直徑1.4 cm 的圓,用于提出粒子坐標.把“十”字形結構用愛牢達膠粘貼于hexbug 馬達的背部(圖1(c)),作為具有自驅能力的基本組裝單元.

實驗場地由2.2 m×2.2 m 的玻璃板構成,表面噴上黑色亞光漆,方便粒子識別.邊界是由泡沫塑料板制成的八瓣梅花形邊界,高5 cm,邊界每條圓弧皆為半徑40 cm,124°的圓弧.場地長212.5 cm,總面積為32566.60 cm2(圖1(d)).預先設想了若干種二、三、四聚體可能的構型(圖1(e)—(g)),將它們分別擺放于場地中央并開始拍攝.

圖1 實驗材料與場地 (a) hexbug 馬達;(b) 識別卡片,白點用于提取坐標,數字代表對應部分的尺寸;(c) hexbug 馬達與“十”字形結構復合體;(d) 實驗場地,數字表示對應尺寸,白色表示梅花邊界;(e)—(g) 二聚體、三聚體、四聚體的初始結構Fig.1.Experimental setup:(a) Hexbug motor;(b) identification card,white dots used to extract the coordinate;(c) complex of hexbug motor and“十”structure;(d) experiment field (the white color denotes the plum flower border);(e)–(g) the initial structure of dimer,trimer and tetramer.

拍攝使用的是Basler 攝像頭(https://zh.docs.baslerweb.com/aca4024-29um),被放置于場地的正上方,拍攝幀率為每秒鐘14.00 幀.拍攝完成后,照片通過ImageJ 處理后用IDL 程序提取卡片上白點的坐標,作為粒子幾何中心的坐標.

從實驗中可以看出,寡聚體在運動過程中十分穩定.因此,將寡聚體視作剛體來進行分析.主要分析了寡聚體的幾何中心的均方位移和寡聚體整體轉動的均方角位移.寡聚體幾何中心的計算公式:

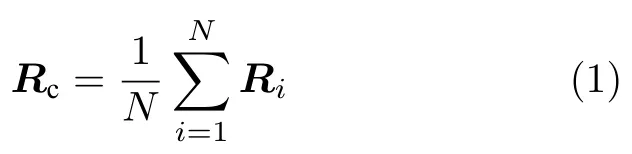
其中N為聚集體數目;Ri為第i個自驅動單元的幾何中心.寡聚體的均方位移(MSD(t))定義為

〈·〉表示時間和系綜平均,每個構型分別做了3 次實驗,進行系綜平均.一般情況下,MSD(t) 正比于tα,α是冪率因子,α2代表彈道運動,1<α<2代表超擴散行為,α1表示正常擴散,α<1 表示亞擴散行為.同理,均方角位移定義為

其中θ(t)表示經歷t時刻后轉過的角度;β的物理意義,類似于α,表示寡聚體旋轉擴散行為.

物理圖像上分析,若把寡聚體看作剛體,則其運動應遵從如下平動和轉動方程:

其中Fc為一個寡聚體受到的合力,Γ為寡聚體受的總力矩,γt與γr為平動與轉動摩擦系數,m和I是聚集體總質量和轉動慣量.η(t)與ξ(t) 為噪音導致的隨機力,噪音來源于馬達的振動,不一定滿足漲落耗散定理.需要說明的是,因為實驗上很難獲得寡聚體的重心,用幾何中心代替重心,也就是說幾何中心的運動實際上是偏心運動.由于整個實驗體系為過阻尼體系,平動與轉動加速度皆可視為零,可解出如下方程:

因此從理論上來說,質心軌跡應該作圓周運動,而圓周運動的中心會由于隨機力的關系產生波動,接下來將對于不同的構型進行單獨分析.

3 結果與討論

3.1 二粒子體系

如圖2(a)所示,二聚體有三種可能構型,分別標記為2-1,2-2,2-3.三種構型幾何形狀上沒區別,唯一不同的是自驅動力的取向.2-1 和2-2 驅動力方向都是反平行的,但自驅力取向之間的垂直距離2-2 是2-1 構型的二倍.2-3 構型中,自驅動力方向相互垂直.首先研究了三種構型的動力學行為,這三種構型幾何中心的軌跡如圖2(b)—(d),可以明顯地看出三種構型都存在偏心旋轉.在2-1 與2-2構型的運動中,軌跡顯示偏心旋轉形成的圓周半徑很小(圖2(b)和圖2(c)),軌跡更多地表現出中心的平動.這主要是由于兩個粒子自驅動力相對于幾何中心產生的扭矩同向,對整體轉動有加強作用;而力的方向平行、反向,相互削弱,最終是軌跡展現出來較快的轉動和較慢平動的軌跡圖像.實驗上,受場地和振動噪音的影響,很難確保兩粒子自驅動力大小相等,因此旋轉中心會偏離幾何中心,中心平動軌跡也有差異.2-3 構型中,自驅動力合力不為零,平動速度會變快,導致偏心旋轉形成的圓周半徑尺寸變大(圖2(d)).

THZ-82A型水浴恒溫振蕩器，常州潤華電器有限公司產品；SPECORD 210 Plus型全自動紫外可見光譜儀，德國耶拿分析儀器股份公司產品；DELTA 320型pH計，梅特勒-托利多儀器有限公司產品。

為定量研究二聚體幾何中心的平動動力學,圖3(a)給出了其均方位移.對于2-1 構型,幾何中心在0 1.7時,MSD 呈現振蕩狀態,這是由于2-3 構型做圓周運動.

二聚體的轉動,可以用角平均位移表征.從圖3(b)可以看出,三種構型都以恒定的角速度進行旋轉,擬合得到的角速度ω分別約為2.6,3.5,0.9 rad/s.2-2 構型的角速度在三種構型中最大,這是因為這種構型的力矩是三種構型中最高的,如圖2(a)所示,假設質量均勻分布,幾何中心為其質心,則力矩約為2aF(a為“十”字形粒子邊長,F為自驅動力),2-3 構型的角速度在三種構型中最小,這是因為它的力矩在三種構型當中最小,約為0.5aF.值得注意的是,雖然這三種構型的力矩成倍率關系,但是角速度卻沒有成倍率關系,猜測:一是由于它們底部的hexbug 取向不同,因此轉動慣量和摩擦阻尼也不相同;二是因為粒子的質量分布不均勻,幾何中心與質心不完全相同.

圖2 二聚體構型及運動軌跡 (a) 2-1,2-2,2-3 為三種構型,黃色箭頭為自驅力方向,在每個構型右上角標明了旋轉方向,? 表示順時針旋轉,⊙ 表示逆時針旋轉;(b) 2-1 寡聚體的運動軌跡;(c) 寡聚體2-2 的運動軌跡;(d) 2-3 寡聚體的運動軌跡Fig.2.Structures and trajectories of three dimers.(a) 2-1,2-2,2-3 denote three kinds of arrangements.Yellow arrow is the self-propelled orientation.? means clockwise rotation,⊙ counterclockwise.(b) 2-1 trajectory;(c) 2-2 trajectory;(d) 2-3 trajectory.

圖3 (a) 三種構型的均方位移;(b) 三種構型的角均方位移,插圖為角平均位移;(c) 三種構型的角速度概率分布,其中點代表實驗數據,線條為高斯擬合Fig.3.(a) MSDs for 2-1,2-2,2-3 configurations and their MSADs (b),the inset is mean angle displacement (MAD);(c) angular velocity distribution,where points are the experimental data,lines correspond to Gaussian fitting.

進一步計算了三種構型角速度的分布概率(圖3(c)),角速度的計算采用如下公式:

其中T=1.0/14 為每一幀的時間間隔.對三種構型進行高斯擬合,公式為

其中xc表示對應角速度的平均值,σ對應于角速度的方差.其擬合數據如表1.從圖3(c)可知,2-3 構型的角速度分布要比2-1 與2-2 構型緊密,這是由于2-3 構型進行圓周半徑較大的偏心旋轉,所受噪聲影響小于其余兩種構型.擬合數據和我們用角均方位移給出的結果一致.

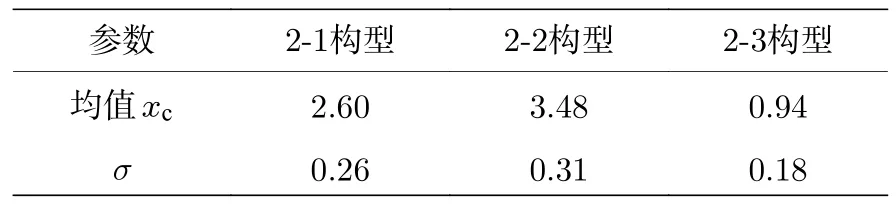
表1 角速度的高斯擬合參數值Table 1.Gaussian fitting parameter value of angular velocity.

3.2 三粒子體系

三粒子的構型比起二粒子多了不少,但是從實驗結果來看,在觀測時間內能保持穩定不解體的只有圖4(a) 所示的四種構型.這四種構型都是從二粒子構型的基礎上增加了一個粒子而成的;3-1 與3-2 構型分別是以2-1 與2-2 構型為基礎,從側面插入一個紅色粒子;3-3 與3-4 構型是以2-3 構型為基礎,分別從不同方向并入一個紅色粒子.首先研究了這四種構型的動力學行為,這四種構型的幾何中心軌跡如圖4(b)—(e).四種構型的自驅動合力不為0 導致它們都在做半徑較大的偏心旋轉.不過,自驅動力取向不同導致偏心旋轉的半徑各不相同.值得注意的是,3-1 與3-4 構型的軌跡為朝一個方向螺旋運動,我們猜測是由于場地沒有完全水平,使3-1 與3-4 構型受到了重力的影響開始偏移;3-2 與3-3 構型受重力影響較小,從軌跡中可以看出,由于噪聲的關系,它們偏心旋轉的圓心一直在移動.

圖4 三粒子寡聚體構型及運動軌跡 (a) 四種構型,黃色箭頭為自推進力方向,在每個構型旁邊標明了旋轉方向,? 表示順時針旋轉,⊙ 表示逆時針旋轉;(b) 3-1 的運動軌跡;(c) 3-2 的運動軌跡;(d) 3-3 的運動軌跡;(e) 3-4 的運動軌跡Fig.4.Structures and trajectories of three trimers.(a) 3-1,3-2,3-3,3-4 denote four kinds of arrangements.Yellow arrow is the selfpropelled orientation.? means clockwise rotation,⊙ counterclockwise.(b) 3-1 trajectory;(c) 3-2 trajectory;(d) 3-3 trajectory;(e) 3-4 trajectory.

為了定量研究三聚體幾何中心的平動動力學,計算了它們的均方位移(圖5(a)).這四種構型的均方位移都是在短時間尺度上表現為超擴散,在長時間尺度上表現為振蕩狀態,這是由于這四種構型都在做圓周運動.3-1 構型,在0

圖5 (a) 四種構型的均方位移;(b) 四種構型的角均方位移,插圖為角平均位移;(c) 四種構型的角速度概率分布及高斯擬合;(d) 四種構型的曲率概率分布及高斯擬合Fig.5.(a) MSDs for 4-1,4-2,4-3,4-4 configurations;(b) MSADs for four configurations,where the inset is mean angle displacement;(c) angular velocity probability distributions and their Gaussian fittings;(d) curvature probability distributions and their Gaussian fittings.

三聚體的轉動,可以用角平均位移表征.從圖5(b)可以看出,三種構型都以恒定的角速度進行旋轉,擬合得到的角速度ω分別為1.01,1.54,0.68,1.95 rad/s.其中3-4 構型的角速度是最大的,并且它的力矩是所有構型中最大的,約為10aF/3;3-3 構型的角速度是最小的,而它的力矩約為aF,是這四種構型中最小的.值得注意的是,3-1 構型的力矩與3-3 構型相同,都為aF,但是3-3 構型的角速度比3-1 構型要小,這是由于兩者幾何構型不同.

表2 角速度的高斯擬合參數值Table 2.Gaussian fitting parameter value of angular velocity.

為了探究這四種構型所做圓周運動的差別,計算了質心曲率分布的概率.計算曲率的公式為

其中

為了減小誤差,時間間隔定為5 幀.四種構型的曲率概率分布如圖5(d)所示,將其進行高斯擬合,參數如表3.其中3-3 構型的曲率最小,分布最緊密,猜測是因為其曲率過小,平動較為明顯而減小了噪聲的影響;3-4 構型的曲率最大.發現對于這四種構型,角速度越大,其運動軌跡的曲率也越大.

表3 轉動圓周曲率的高斯擬合參數值Table 3.Gaussian fitting value of curvature.

3.3 四粒子構型

如圖6(a)所示,研究了四粒子的5 種構型.4-1構型以二粒子為基礎,在左右兩側分別插入了一個粒子(圖6(a)中紫色與藍色);4-2 構型是四個粒子從不同方向合并在一起的一個類方形構型;剩下三種構型的都是以一個粒子為中心(圖6(a)中綠色粒子),其余三個粒子聚集在該粒子上形成的,不同點是4-3 構型與其余兩種的幾何構型不同,4-4與4-5 構型中心粒子的極性方向不同.首先研究了這五種構型的動力學,其幾何中心的運動軌跡如圖6(b)—(f).這五種構型軌跡都在進行偏心旋轉,但是前四種構型與2-1 和2-2 構型類似,構型中的粒子相對于幾何中心產生了同向的力矩,加強了整體轉動,自驅動力之間的方向兩兩反向平行,相互削弱,因此最終軌跡與2-1 和2-2 構型類似,圓周半徑很小,表現出來較快的轉動與較慢平動軌跡的圖像.4-2 與4-3 構型所作的偏心旋轉較為明顯,進行螺旋運動.4-5 構型其自驅力合力不為0,平動速度較快,展現出了半徑較大的偏心旋轉.

圖6 四粒子寡聚體構型及運動軌跡 (a) 4-1,4-2,4-3,4-4,4-5 為五種構型,黃色箭頭為自推進力方向,在每個構型旁邊標明了旋轉方向.? 表示順時針旋轉,⊙ 表示逆時針旋轉.(b) 4-1 的運動軌跡;(c) 4-2 的運動軌跡;(d) 4-3 的運動軌跡;(e) 4-4 的運動軌跡;(f) 4-5 的運動軌跡Fig.6.Structures and trajectories of five tetramers:(a) 4-1,4-2,4-3,4-4,4-5 denote five kinds of arrangements.Yellow arrow is the self-propelled orientation.? means clockwise rotation,⊙ counterclockwise.(b) 4-1 trajectory;(c) 4-2 trajectory;(d) 4-3 trajectory;(e) 4-4 trajectory;(f) 4-5 trajectory.

研究了這幾種構型的平動動力學,計算了它們的均方位移(圖7(a)).對于4-1 構型,在0

接著計算了五種構型的角均方位移(如圖7(b)).從圖7(b)可知,這五種構型也是以恒定的角速度進行旋轉的.這五種構型的角速度分別為1.96,1.54,1.79,1.79,1.45 rad/s.4-1 構型的角速度最大,這是由于在這五種構型中它的力矩最大,4-2 構型的角速度最小,力矩也最小;值得注意的是,4-3 與4-4構型的角速度一樣,幾何構型也相似.

圖7 (a) 五種構型的均方位移;(b) 五種構型的角均方位移,插圖為角平均位移;(c) 五種構型的角速度概率分布Fig.7.(a) MSDs for five structures and (b) their MSADs.The inset is mean angle displacement.(c) Angular velocity distributions for five structures.

為了進一步分析五種構型的動力學,還研究了這五種構型的角速度分布,如圖7(c).4-1 構型的峰寬較寬,峰值處角速度為1.70—2.20 rad/s;4-2構型的峰值為1.52—1.55 rad/s;4-3 構型的峰值為1.78 rad/s,4-4 構型的峰值為1.76 rad/s,4-5 構型的峰值為1.44 rad/s.從圖7(c)可以看出,4-1 構型的角速度范圍最大,原因是三次實驗給出的角速度分布差異過大,統計合并后導致出現了平臺區;4-3 與4-4 構型的角速度分布較為相似,這是由于它們的構型較為相似.

3.4 討論

從動力學的角度來看,寡聚體的動力學與其組裝方式有關.自驅動粒子所產生的力矩使寡聚體轉動,噪聲與自驅動力使寡聚體進行平動.上述所描繪的構型皆存在力矩,因此它們都會進行轉動,其中一部分構型自驅動力的理論合力為零,但由于活性粒子因樣品不同,因此聚集體會在噪聲與自驅動力的作用下表現為轉動與平動的耦合,另一部分合力不為0 的構型則呈現為圓周半徑較大的偏心轉動.我們發現,這些構型在短時間都會因為轉圈而進行持續時間為1—2 s 的超擴散運動,且持續時間長短與其角速度有關,在其首次運動大半圈的時間內都會進行超擴散運動,因此各個構型的持續時間與角速度的乘積較為相近,大約在200°.由于實驗中的“十”字形粒子有差異且底盤有質量分布不均勻的馬達,每種構型的轉動慣量難以測量,因此只能大致觀測出每種寡聚體的動力學與其構型之間的關系.構型的總力矩越大,轉動慣量越小,其角速度也就越大.關于其構型與動力學之間的定量關系(如角速度大小等),我們今后會通過模擬的方法展開進一步研究.

由于這些寡聚體相互之間沒有吸引相互作用,粒子之間僅通過自驅動力而結合在一起,因此組裝的構型并不都很穩定.圖8 給出了兩種不穩定的構型.首先是圖8(a),構型在運動的過程中綠色粒子與藍色粒子很容易就會分開,變成兩個二聚體.這是因為紫色粒子會給綠色粒子施加扭矩,導致綠色粒子逆時針旋轉,脫離聚集體.圖8(b)的幾何構型和4-4,4-5 構型類似,但是不同的是,圖8(b)中綠色粒子施加在紫色、藍色、紅色粒子形成的寡聚體上的力矩和寡聚體本身的轉動方向相反,因此在運動過程中綠色粒子容易脫離構型.從這些例子可以看出,構型要想穩定存在,應該要滿足一定的條件.在這里我們做出一些猜測:構型中的粒子自推進力方向朝著質心的一般較為穩定,不然構型容易在自驅力方向偏離質心的粒子的作用下解體,如圖8(a)構型;構型中貢獻負力矩(與原寡聚體轉動扭矩相反)的粒子越少,構型越穩定,否則構型中的粒子會在旋轉過程中與原寡聚體分開,如圖8(b)構型所示.寡聚體的構型不僅影響其動力學,也影響著構型的穩定性.而具體構型與穩定性的關系,今后將進行更進一步的研究.

圖8 兩種不穩定的四聚體構型Fig.8.Two different structures of four polymers which are instable.

通過這些對于“十”字形寡聚體的研究,可以對大量“十”字形粒子的自組裝做出一個大致的預測.“十”字形粒子在運動的過程中首先會相互接近組合成各種寡聚體,一部分寡聚體穩定存在,一部分不穩定的會在運動中解體形成新的較為穩定的寡聚體.接著由于一部分寡聚體會進行半徑較大的圓周運動,數個寡聚體會相互接觸再組裝成新的較為穩定的大團簇,產生新的運動軌跡,再與其他寡聚體進行接觸,最終大團簇會吸收大部分的“十”字形粒子,形成一個最大的團簇,完成自組裝,產生相分離現象.

4 結論

本文設計了一種“十”字形活性粒子,發現在實驗中這些“十”字形粒子可以形成穩定性很好的寡聚體,而研究這些寡聚體的動力學行為可以幫助我們更好地理解大量粒子的自組裝行為.實驗研究了它們的運動軌跡、均方位移、角速度、角速度分布概率以及曲率分布概率.這些構型的質心軌跡大致分為兩類,第一類的幾何構型自推進力合力為0,質心運動為較快轉動與較慢平動相結合的運動模式,這是由于實驗中有熱噪聲以及自驅動力有漲落,合力不完全為0,這種類型的均方位移表現為反常擴散;第二類的幾何構型自推進力合力不為0,質心運動為圓周半徑較大的偏心旋轉運動,其曲率與自身構型有關,這種類型的均方位移在小時間尺度上表現為反常擴散,時間長短與角速度有關,通常持續1—2 s.在旋轉動力學上,所有的構型都有著力矩,因此也都進行旋轉,其旋轉速度與其力矩大小和幾何構型有關,寡聚體結構的總力矩越大,轉動慣量越小,其角速度也會越大.對于三聚體,還研究了其曲率概率分布,發現三聚體的角速度越大,相應地其曲率也越大.寡聚體的旋轉平動和轉動動力學對于大量“十”字形自驅馬達組裝行為的影響,將在未來的工作中進行進一步研究.