渦旋光束在雙拉蓋爾-高斯旋轉腔中的非互易傳輸*
朱雪松 劉星雨 張巖
(東北師范大學物理學院,物理學師范專業國家級實驗教學示范中心,長春 130024)
通過構造兩個線性耦合的拉蓋爾-高斯旋轉腔系統,實現攜帶軌道角動量的渦旋光束的非互易傳輸現象.系統中,兩個拉蓋爾-高斯旋轉腔模通過扭力與中間的旋轉鏡耦合,同時兩個渦旋腔場通過光纖直接耦合起來.兩個強光場分別驅動不同的腔模,并利用一個弱探測場從系統一側入射,從而對該系統兩個傳播方向的光響應特性進行研究.利用該系統哈密頓量和海森伯-郎之萬方程,結合輸入-輸出關系可得到系統的輸出光譜.結果表明此系統中的渦旋光束的非互易性來源于光旋轉相互作用以及渦旋腔場相互作用之間的量子干涉效應.因此,可以通過調節非互易相位差來對系統的非互易傳輸進行調制.此外,兩個渦旋光束所攜帶的拓撲荷比值會顯著影響傳輸特性;在適當的拓撲荷比值下,該系統可以實現渦旋光束的單向傳輸.本研究成果有望用于實現理想的渦旋光隔離器.
1 引言
由于在空間光通信、量子糾纏、粒子操控等領域的應用,光學渦旋已成為近年來的研究熱點.與普通光束相比,渦旋光束可以攜帶軌道角動量.拉蓋爾-高斯(L-G)光束就是一種典型的渦旋光束,其具有螺旋相位結構和環形場強分布,光束中心的強度為零[1].L-G 光束沿其傳播方向攜帶每光子??的軌道角動量,?表示L-G 光場的拓撲荷數[2].
實驗表明,通過交換軌道角動量,L-G 光束可以對物體施加扭矩,包括微觀吸附顆粒[3]、介觀玻色-愛因斯坦凝聚[4]及亞微米布朗粒子[5].2007 年,基于此性質,拉蓋爾-高斯旋轉腔系統被提出[6],該系統由兩個用作腔鏡的螺旋相位元件構成,分別為一個固定腔鏡和一個圍繞腔軸旋轉的旋轉腔鏡(可視為扭擺).在這種光旋轉系統中,腔模是L-G 光,它攜帶軌道角動量,可以與螺旋相位元件交換軌道角動量.近期人們對此類系統的興趣逐漸增加,并做了一些相關研究,包括旋轉腔鏡的冷卻[6,7]、光場軌道角動量的檢測[8,9]、二階邊帶效應[10]和糾纏[11,12].然而,據我們所知,關于L-G 光束在拉蓋爾-高斯旋轉腔中的非互易傳輸現象至今還未被報道過.由于光旋轉相互作用[13]和光機械相互作用[14,15]之間存在類似的哈密頓量,光機械相互作用產生的許多效應[16?29],在拉蓋爾-高斯旋轉腔中通過與L-G 光場軌道角動量的交換也會發生[6?12].這為利用光的軌道角動量而不是動量提供了可能性.
光的傳播通常是互易的,不過實現光學非互易對于構建非對稱量子網絡極為重要.光學非互易性描述的是光場從一個方向通過光學系統但是不能沿原路返回的特性.光學非互易是實現定向放大器、隔離器、循環器的基礎[30],并且需要打破時間反演對稱性.傳統上,非互易傳輸依賴于施加的偏置磁場[31],但這些傳統器件通常體積龐大,與超低損耗超導電路不兼容,并且需要相當大的磁場.近年來,有人利用輻射-壓力誘導光力耦合來打破時間反轉對稱性,實現光的非互易效應[32?46].這一領域已經取得了重要成果,包括非互易傳輸和放大[32?34]、非互易單光子效應[35]、非互易慢光[37]等.文獻[38]提出了一種基于具有光增益的光機械系統來實現光場和微波場之間光定向放大的方案,發現放大方向可以通過調節有效光機耦合之間的相對相位(非互易相位差[46])來控制.文獻[43]給出了由兩個光學膜和一個機械模組成的三模光機械系統中的光學非互易響應,并證明了光學非互易響應是通過調節光機械耦合速率之間的相位差來打破系統的時間反轉對稱性來實現的.然而,通過光旋轉耦合來實現攜帶軌道角動量的渦旋光束的非互易傳輸還有待進一步研究,且之前工作在利用光力耦合來實現普通光束的非互易傳輸時,都是利用光學模式與機械模式交換動量來實現,而非交換角動量.
本文通過在單個拉蓋爾-高斯旋轉腔中額外加一個固定腔鏡來構建雙拉蓋爾-高斯旋轉腔,并通過光纖將兩個腔模線性耦合,并且用兩個強驅動場驅動不同的腔模,進而研究渦旋光束的非互易傳輸現象.將以往通過光與機械振子交換動量來實現普通光束的非互易傳輸推廣到光與旋轉腔鏡交換角動量來實現渦旋光束的非互易傳輸.研究發現,非互易相位差可以決定渦旋光束非互易傳輸的產生及方向;在一定的拓撲荷比值下,該系統可以實現完美的非互易性;系統耗散對傳輸振幅的變化有比較大的影響;此外,通過調節非互易相位差,在該系統中可以實現非互易的慢光效應.在此系統中的渦旋光束傳輸的非互易性,來源于光旋轉耦合相互作用和腔模耦合相互作用形成的兩條路徑之間發生的量子干涉效應.
2 理論模型與主要公式
如圖1 所示,本方案考慮了雙拉蓋爾-高斯旋轉腔光旋轉系統,其中3 個腔鏡均為螺旋相位元件,其中兩個輸入腔鏡部分透明且剛性固定,不改變透過它們光束的軌道角動量而會給反射光束增加 ?2?1和 ?2?2的拓撲荷;處于中間位置的旋轉腔鏡是完全反射的,可以給反射光增加 +2?1和+2?2的拓撲荷,并可以在支架上繞腔軸z旋轉(角平衡位置φ00);同時兩個腔場通過光纖線性耦合在一起.兩個頻率均為ωc,振幅分別為εc和εd的強驅動場分別從兩側注入系統驅動頻率為ω0的L-G 腔模.利用一束頻率為ωp、振幅為εL(εR)的弱探測場從系統左側(右側)入射,從而檢查該光旋轉系統相對于左側(右側)探測光的響應特性.在驅動場頻率ωc的旋轉框架下,系統的哈密頓量(?=1)可寫為
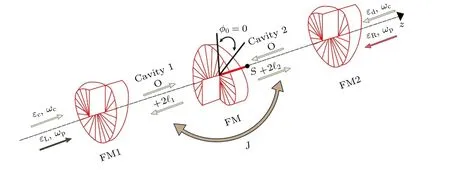
圖1 雙拉蓋爾-高斯旋轉腔示意圖,兩L-G 腔場通過光旋轉相互作用與中間的旋轉腔鏡耦合,振幅為 εc和 εd (εL和 εR)的強驅動場(弱探測場)分別從兩側入射系統來驅動L-G 腔模 c1和 c2,同時用光纖將兩L-G 腔模線性耦合.旋轉腔鏡的平衡位置為 φ0,在扭力作用下的角位移用 φ 角表示Fig.1.Schematic diagram of double Laguerre-Gaussian (L-G) rotational-cavity.The two L-G cavity modes are coupled with a rotating cavity mirror in the middle via the optical rotation interaction.Two strong pump fields (weak probe fields) with amplitudes εcand εd(εLand εR) are incident on the system from both sides to drive the L-G cavity modes c1and c2,and the two L-G cavity modes are linearly coupled with an optical fiber.The equilibrium position of the rotational mirror is φ0,and the angular displacement is indicated by angle φ under the action of the torsion.
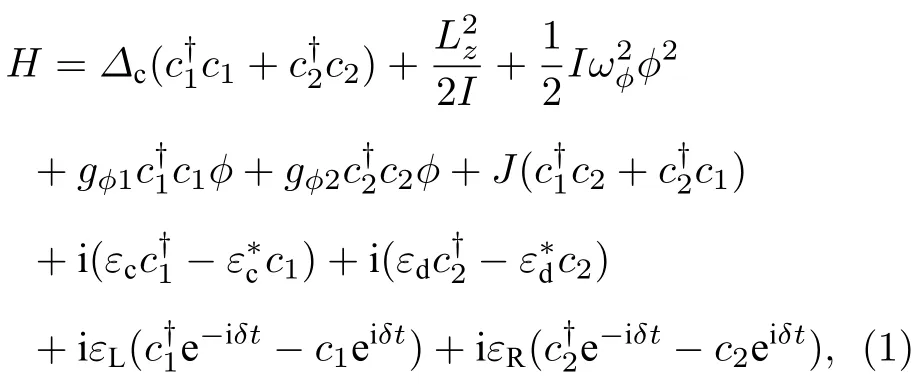
式中,第1 項表示L-G 腔模的自由哈密頓量,其中c1和為兩個腔的湮滅(產生)算符,Δcω0?ωc為驅動場與腔模的失諧;第2 項和第3 項給出了旋轉鏡的自由哈密頓量,ωφ,Lz和φ分別為旋轉鏡的角頻率、角動量和角位移,IMR2/2 為旋轉鏡的轉動慣量,其中M和R分別為旋轉鏡的質量和半徑;第4 項和第5 項表示L-G 腔模與旋轉鏡的光旋轉耦合,單光子耦合強度分別為gφ1c?1/L和gφ2c?2/L,其中L為兩個腔的長度;第6 項表示兩個腔模的線性耦合,其中J為線性耦合強度;最后4 項分別表示強驅動場和弱探測場對腔模的驅動,δωp?ωc為探測場與驅動場之間的失諧.

由系統的哈密頓量,可以寫出描述系統的動力學的相關算符的海森伯-郎之萬方程:
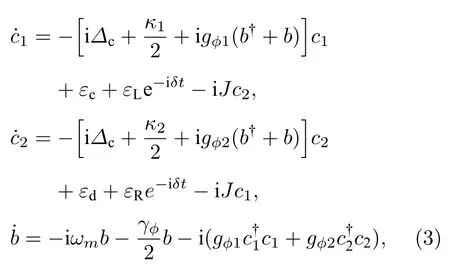
其中κj和γφ分別為兩腔和轉動腔鏡的弛豫速率.在乘積算符的平均值滿足分解假設〈bcj〉〈b〉〈cj〉且忽略探測場的情況下,可得到算符的穩態解:
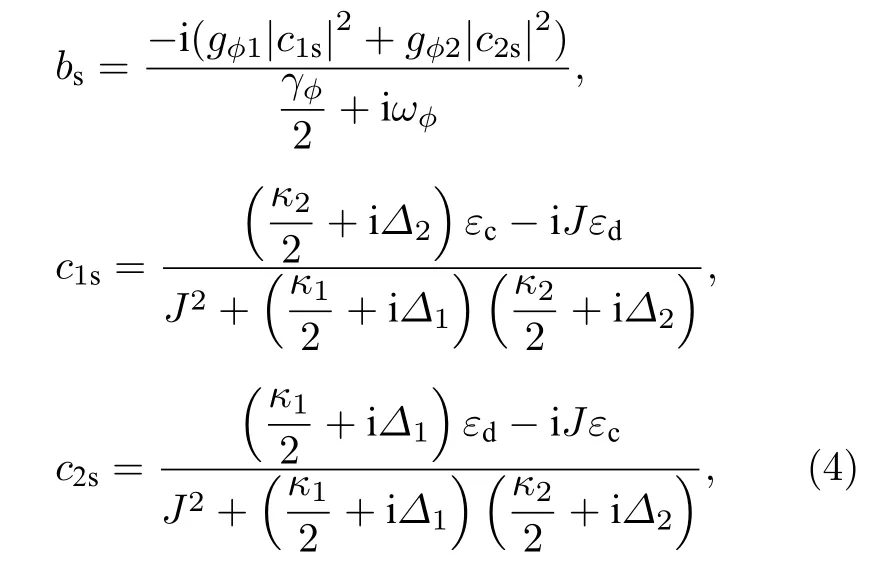
其中Δ1,2Δc+gφ1,φ2(bs+) 為L-G 腔模和驅動場之間的有效失諧.
在強驅動場的驅動下,每個算符可以由其平均值和量子漲落的和表示,即cjcjs+δcj,bbs+δb.將cj和b的表達式代入方程(3),可以得到線性化的海森伯-郎之萬方程:
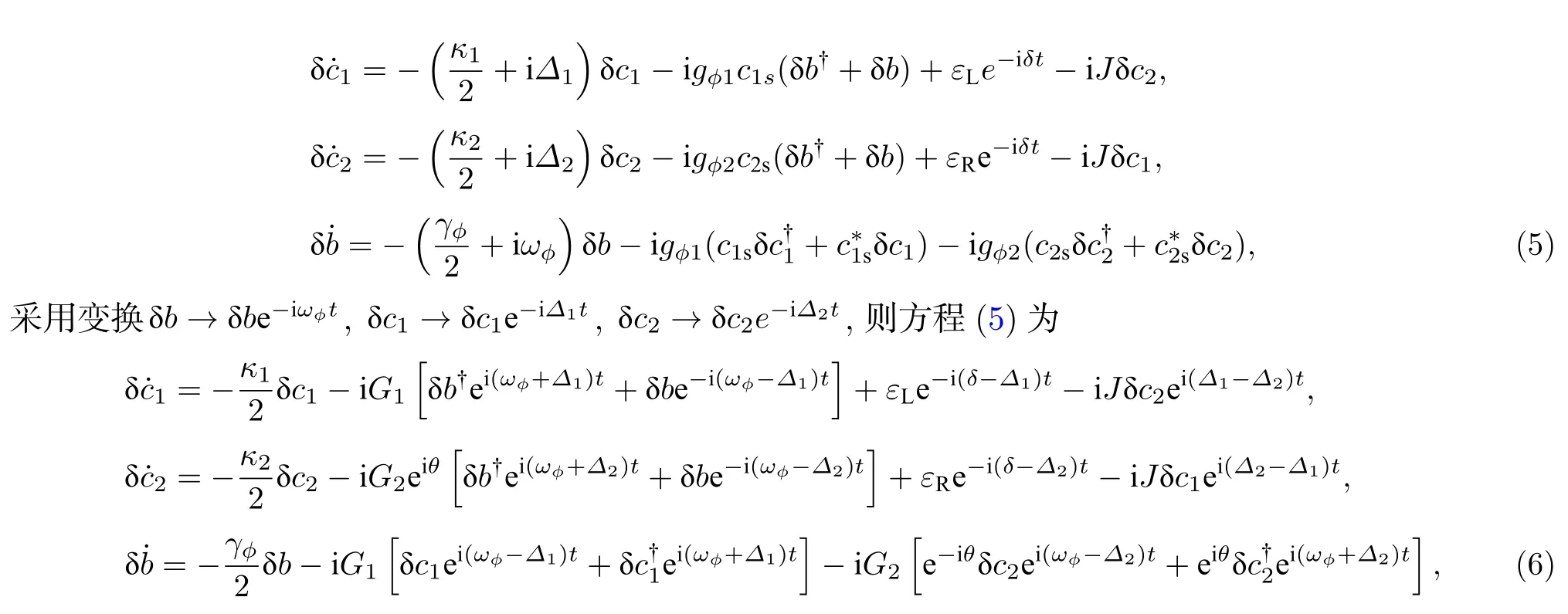
其中G1,G2為兩個渦旋腔場與旋轉腔鏡之間的有效光旋轉耦合強度,gφ1c1s和gφ2c2s之間的非互易相位差θ可以通過驅動場εc和εd的相對相位來調節.
如果每個強驅動場都處于力學紅邊帶(Δ1≈Δ2≈ωφ),同時旋轉鏡頻率ωφ遠大于有效耦合強度Gj,方程(6)可以化簡為
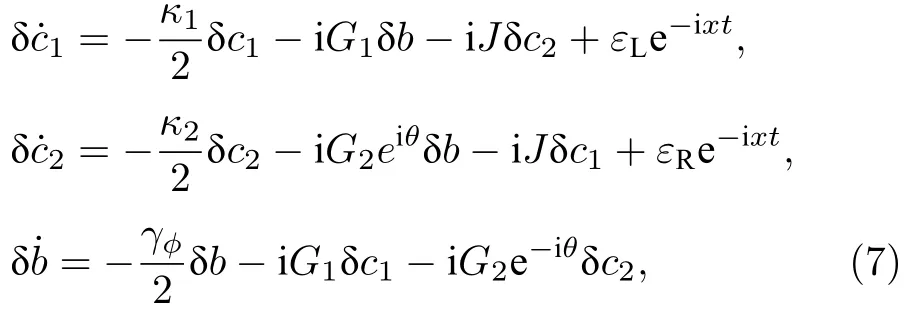
其中xδ ?ωφ.由方程(7)的具體形式,可以假設方程(7)的解具有下面的形式:
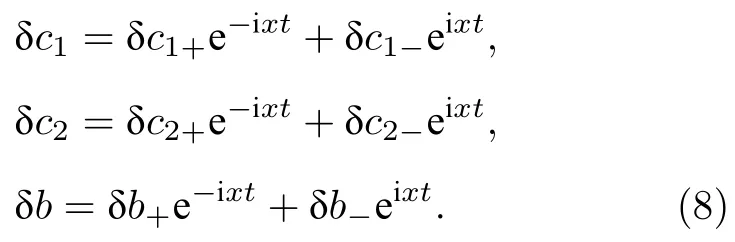
將方程(8)代入方程(7)得
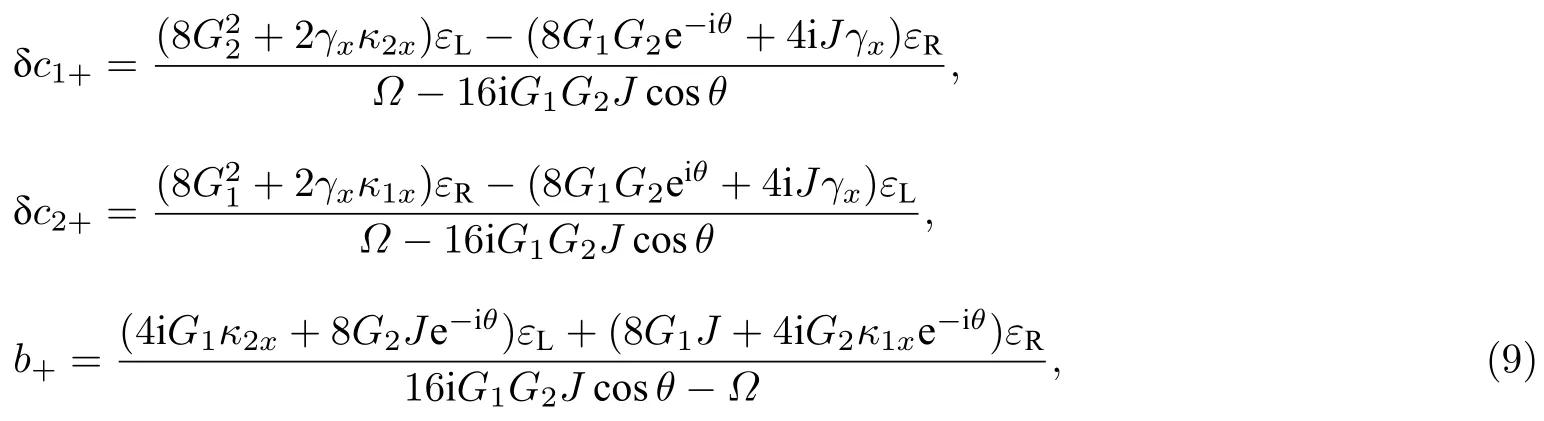

本文定義T12(T21)為入射腔c1(c2) 的探測場通過系統后輸出時的傳輸振幅,根據(9)式和(11)式計算得
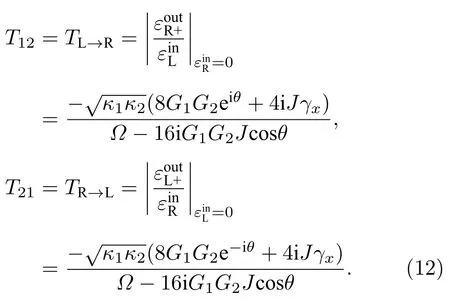
3 渦旋光束傳輸非互易性
本節將詳細說明在雙拉蓋爾-高斯旋轉腔系統中非互易相位差θ、渦旋光束所攜帶拓撲荷?和系統耗散對傳輸振幅的影響.首先討論非互易相位差θ對傳輸振幅的影響.
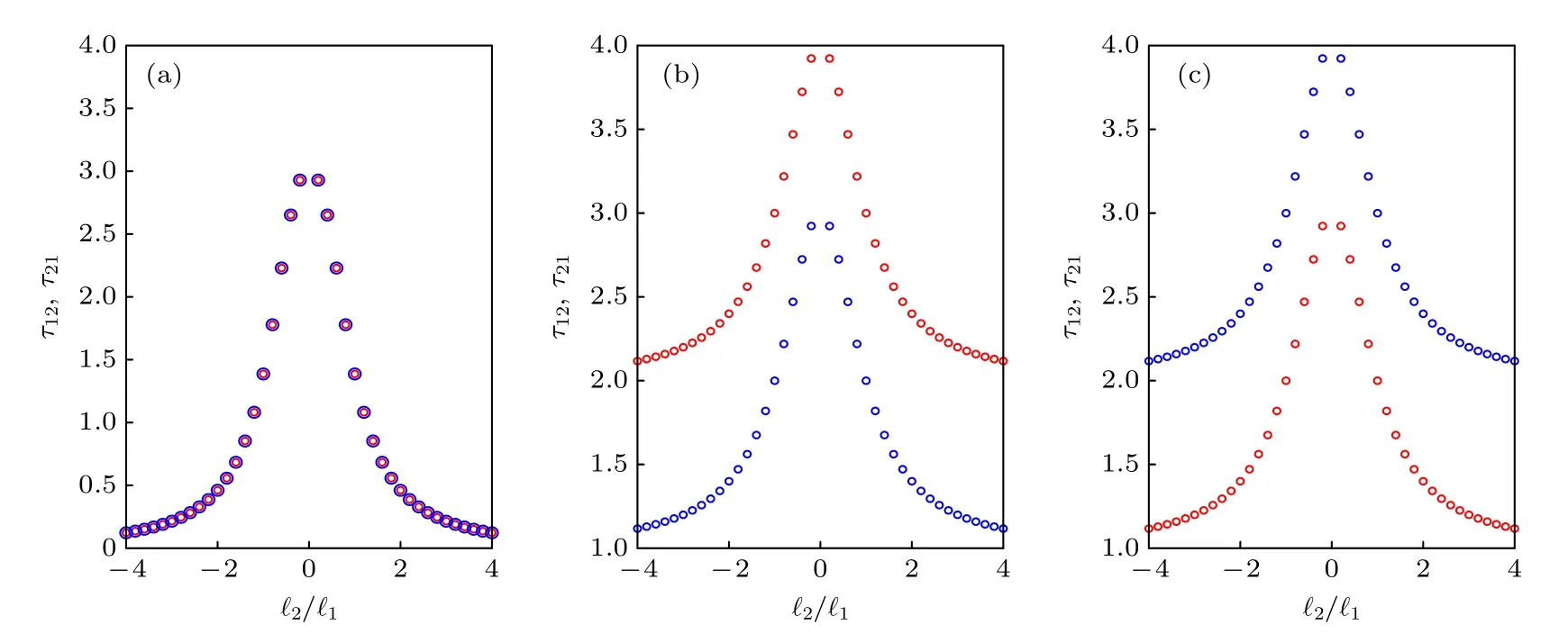
圖2 給出傳輸振幅T12(紅色實線)和T21(藍色虛線)在不同非互易相位差θ下隨標準化失諧x/κ1的演化.可以看出,相位差θ對渦旋光束傳輸有比較大的影響,在θ=0 時,探測場在兩個方向上的傳輸是互易的,但當0 探測場的傳輸會呈現明顯的非互易性.觀察圖2(b)—圖2(e)可以發現,非互易現象會出現在共振點及附近,還可以發現相位差的正負可決定非互易的方向(θ <0時,T21>T12;而θ >0時,T21 圖2 傳輸振幅 T12(紅色實線)和 T21(藍色虛線)在不同非互易相位差 θ下隨標準化失諧 x/κ1的演化 (a) θ0;(b) θ?π/4 ;(c) θπ/4;(d) θ?π/2;(e) θπ/2 .(f)在標準化失諧為零(x =0)時,傳輸振幅 T12(紅色實線)和 T21 (藍色虛線)隨非互易相位差 θ 的演化.其他參數為 κ1 1,κ2 1,γ1 ,Gi Fig.2.Transmission amplitudes T12(red solid line) and T21(blue dotted line) versus normalized detuning x/κ1 under different nonreciprocal phase difference:(a) θ0;(b) θ?π/4;(c) θπ/4;(d) θ?π/2;(e) θπ/2 .(f) Transmission amplitudes T12(red solid line) and T21(blue dotted line) versus nonreciprocal phase difference with x0 .Other parameters are κ1 1,κ2 1 ,γ1 ,Gi 接下來討論系統耗散對渦旋光束傳輸非互易性的影響.為不失一般性,取非互易相位差θπ/2 .圖3(a)和圖3(b)給出了傳輸振幅T12和T21在旋轉腔鏡的不同耗散率γ下隨標準化失諧x/κ1的演化.可以看出在共振點(x=0)附近,隨著旋轉鏡耗散率γ增加,從腔c1到腔c2的傳輸振幅T12=1 保持不變,而從腔c2到腔c1的傳輸振幅T21呈現出明顯的變化,顯示出先降低后增加的趨勢.當旋轉鏡耗散率γ=κ1=1 時,渦旋光束的傳輸非互易性達到最佳(T121,T210,在共振點處). 圖3(c)和圖3(d)給出了傳輸振幅T12和T21在腔c2的不同耗散率下隨標準化失諧x/κ1的演化.可以看出,在共振點(x=0)附近,隨著腔c2耗散率κ2增 加,從腔c2到腔c1的傳輸振幅T21=0 保持不變,而從腔c1到腔c2的傳輸振幅T12呈現逐漸減小的趨勢.當腔c2耗散率κ2=κ1=1 時,渦旋光束傳輸的非互易性達到最佳(T121,T210,在共振點處).所以對于渦旋光束的非互易傳輸來說,腔場c2的耗散不是越低越好. 接下來討論兩個渦旋光場所攜帶拓撲荷比值?2/?1對傳輸振幅的影響.通常,渦旋光場所攜帶拓撲荷實際上會影響旋轉腔鏡與L-G 腔模的耦合強度.為了方便,這里通過調節驅動場振幅εc和εd的大小從而使得拓撲荷比?2/?1與有效耦合強度比G2/G1相等.圖4(a)—圖4(f)給出了在標準化失諧x=0 時傳輸振幅T12和T21在不同的非互易相位差下隨兩個渦旋光場所攜帶拓撲荷比?2/?1的演化.可以發現,當θ0和θπ 時,拓撲荷的比值對傳輸振幅T12和T21的影響是相同的,即系統對渦旋光束的傳輸呈現互易性.當θ±π/4和θ±π/2時,系統對渦旋光束傳輸呈現明顯的非互易性.當θ±π/4 時,隨著拓撲荷比值的增加,傳輸振幅T12和T21的變化趨勢是相同的,且是偶對稱,但相同拓撲荷比值所對應的傳輸振幅T12和T21是不同的,在拓撲荷比值為±1 處的非互易性是最好的.當θ±π/2 時,隨著拓撲荷比值的增加,傳輸振幅T12仍呈現關于拓撲荷比值等于 0 處的對稱性,但此時傳輸振幅T21保持為 0 不變.在拓撲荷比值為±1 處,系統對渦旋光束傳輸可以呈現完美的非互易性(T120時T211,或T121時T210).此外,拓撲荷的正負代表渦旋光矢量的旋轉方向,根據渦旋光矢量的旋轉方向可以將渦旋光束分為左旋渦旋光束和右旋渦旋光束.從圖4(d)和圖4(e)可以了解到渦旋光束想要呈現完美的非互易性與渦旋光束的左、右旋無關,只要保證|?2/?1|=1 . 在腔系統中,光的群延遲是描述光群速度的一個重要指標,首先介紹群延遲的定義,即[49,50] 其中Θ21(12)是在頻率為ωp下輸出場c1→c2(c2→c1)的相位,群延遲τij <0對應快光,τij >0 對應慢光. 圖5(a)—圖5(c)給出了針對渦旋光束所對應的群延遲τ12和τ21在不同的非互易相位差下隨兩個渦旋光場所攜帶拓撲荷比?2/?1的演化.在θ0時群速度是互易的且關于拓撲荷比值偶對稱.在θ±π/2時,系統可以呈現明顯的非互易慢光效應,且相位的變化可以影響非互易慢光的群延遲的變換.隨著拓撲荷比值的增加,τ12和τ21均呈現先增大后減小的趨勢且關于拓撲荷比值偶對稱,但群延遲的差值(τ12?τ21或τ21?τ12)一直保持不變. 圖5 群延遲 τ12(紅色圓圈)和 τ21(藍色圓圈)在不同非互易相位差 θ下隨兩個渦旋光場所攜帶拓撲荷比 ?2/?1的演化 (a) θ0 ;(b) θ?π/2;(c) θπ/2 .其他參數為 κ1 1 ,κ2 1 ,γ1 ,J 2G1G2/γFig.5.Group delay τ12(red circle) and τ21(blue circle) with ratio of topological charges carried by two vortex optical fields ?2/?1 under different nonreciprocal phase difference:(a) θ0;(b) θ?π/2;(c) θπ/2 .Other parameters are κ1 1 ,κ2 1,γ 1,J2G1G2/γ . 最后,根據目前的實驗進展,對本文使用的系統方案的可行性進行了討論.本文討論的雙拉蓋爾-高斯旋轉腔系統是在文獻[6]提出的由兩個螺旋相位元件所構成的拉蓋爾-高斯旋轉腔的基礎上,添加一個固定的螺旋相位元件所實現的.通過三個螺旋相位元件作為腔鏡來組成兩個光腔,并且用光纖將兩個光腔線性耦合.其中,兩個輸入腔鏡FM1和 FM2 為部分透明且被剛性固定,不會改變透射光束的軌道角動量但會給反射光束增加 ?2?1和?2?2的拓撲荷,這一效應已經被實驗觀測到[51].另外,處于中間位置的旋轉腔鏡RM 是完全反射的,可以給反射光增加 +2?1和 +2?2的拓撲荷[6].隨著納米技術的發展,螺旋相位元件可以利用超精密點金剛石車削機床直接加工鋁盤表面得到[6,52].利用螺旋相位元件的反射和透射可以改變激光光束的方位結構,進而改變其攜帶的拓撲荷的值.拓撲荷?依賴于螺旋相位元件的結構,通過將螺旋相位元件的方位角坡道劃分為離散的階躍并控制階躍高度和旋向,可以設計出具有特定拓撲荷?的渦旋光場[6,53].最近實驗已經可以通過螺旋相位元件產生攜帶拓撲荷高達1000 的L-G 光束[54].對于本工作,若想實現理想的渦旋光隔離器,就需要在本系統中實現渦旋光束的完美非互易性,即渦旋光束的單向傳輸.在理論分析中得到,若要呈現完美的非互易渦旋光束傳輸,需要保證|?2/?1|=1,因此這里的渦旋光束所攜帶的拓撲荷需是可以調節的.在實驗上,可以通過調整旋轉腔鏡兩側的階躍高度和旋向來實現.另外,理論分析中得到非互易相位差對渦旋光束的非互易傳輸有著重要影響,而非互易相位差的改變在實驗上可以通過調節兩個強驅動激光場εc和εd的相對相位來實現[45].值得強調的是,本文所構建的系統在實驗實現時需要較高精細度的光腔,在光腔的精細度比較低時,在該系統所要探究相關現象會不明顯[53]. 本文研究了渦旋光束在雙拉蓋爾-高斯旋轉腔系統中的非互易傳輸.將以往大多在光機械系統中研究的普通光束的非互易性推廣到在光旋轉系統中研究攜帶軌道角動量的渦旋光束傳輸的非互易性.系統中,光旋轉耦合作用以及光纖的線性耦合作用提供的兩條路徑,從而可以產生量子干涉.首先,研究了非互易相位差對傳輸振幅的影響,發現相位差可以決定渦旋光束非互易性的發生及方向.然后,在相位差θπ/2 時,研究了系統耗散對傳輸振幅的影響,分析了渦旋光束實現完美的非互易傳輸時系統的耗散應該滿足的條件.接下來,分析了渦旋光束攜帶的拓撲荷比值對系統非互易性的影響,探究了實現渦旋光束完美的非互易傳輸時拓撲荷比值應該滿足的條件,發現渦旋光的左、右旋不會對傳輸產生影響.拓撲荷對光傳輸產生影響,主要是因為渦旋光束攜帶的拓撲荷數會影響旋轉腔鏡與腔模的耦合強度.最后,分析了該系統產生的非互易的慢光效應.這些研究成果可用于設計針對攜帶軌道角動量的渦旋光束的理想光隔離器,有望應用于光通信等領域.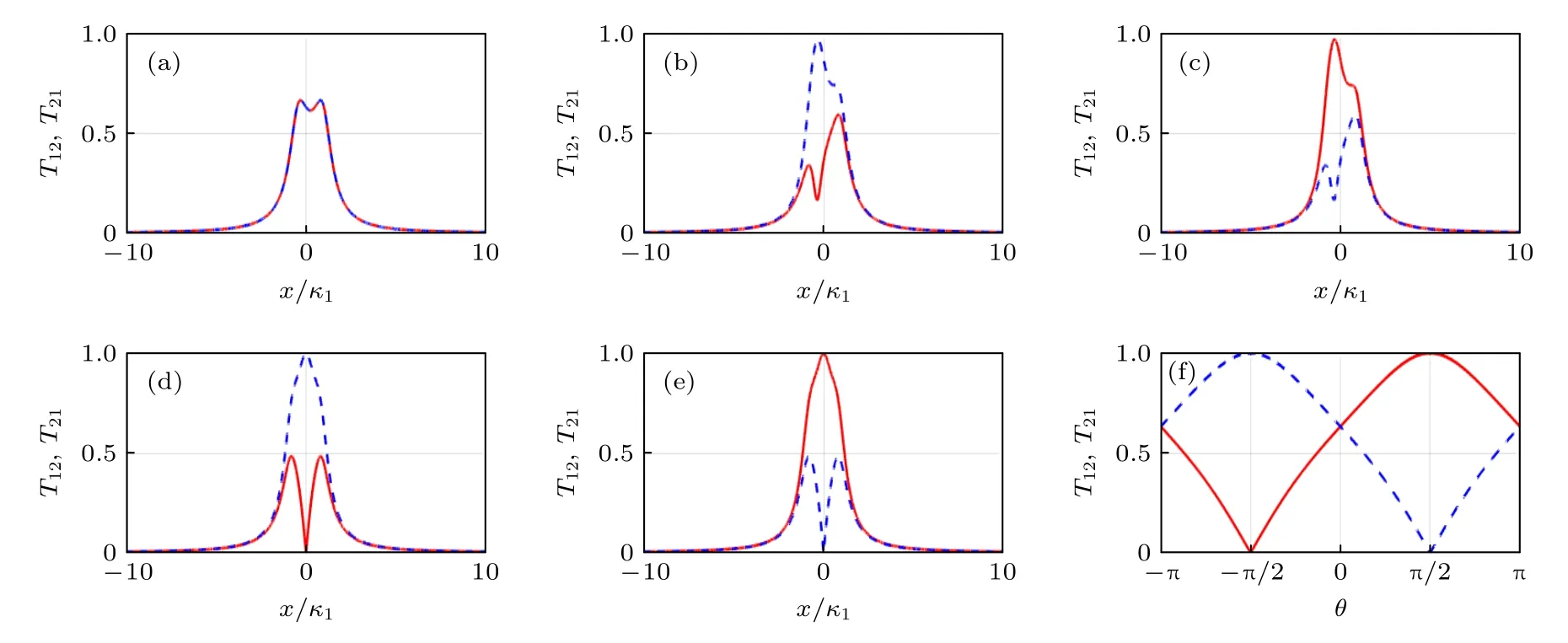
4 非互易慢光效應
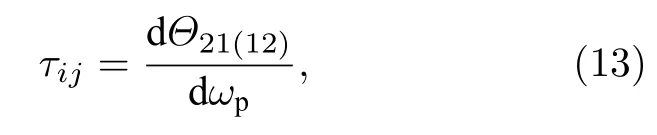
5 實驗可行性分析
6 結論

