耦合Frenkel-Kontorova 雙鏈的格波解及其色散關系*

蘇瑞霞 黃霞 鄭志剛

1) (中國礦業大學(北京) 理學院物理系,北京 100083)

2) (華北電力大學數理學院,北京 102206)

3) (華僑大學信息科學與工程學院,廈門 361021)

求解了兩條相同的耦合Frenkel-Kontorova (FK) 鏈在低溫、有限溫和高溫情況下的格波解及色散關系,進而研究了耦合FK 雙鏈的晶格振動特點.結果表明,耦合FK 雙鏈的色散關系包含一個聲學支和一個光學支,兩者的頻譜范圍和頻率禁帶與FK 鏈的恢復力系數、鏈間耦合強度系數均有關聯,低溫和有限溫的情況還與外勢深度有關系.并且研究發現當鏈間耦合強度較小時,不存在頻率禁帶;當鏈間耦合強度逐漸增加到某一臨界值后,頻率禁帶出現,且隨著鏈間耦合強度增加,頻隙不斷變大,這是因為光學支隨著鏈間耦合強度增加不斷向高頻方向移動.此外,還發現帶隙結構出現的臨界鏈間耦合強度始終為FK 鏈恢復力系數的2 倍,并不受溫度的影響.本文還研究了給定鏈間耦合強度下溫度對耦合FK 雙鏈色散關系的影響規律.本研究內容可為分析鏈間界面耦合和溫度對晶格的振動特點和物理性質的影響提供理論依據,從而對于能量輸運、熱調控等實際應用發揮重要的指導作用.

1 引言

目前中國芯片雖已步入世界領先,但仍存在芯片散熱等卡脖子問題[1?4].而解決這些問題的關鍵步驟一定會涉及到固體中的熱傳導問題和高性能導熱材料.對于固體中的熱傳導可以分為電子導熱和晶格導熱.對于非金屬和一般半導體結構中的熱傳導主要是晶格的導熱,其來源于晶格振動的格波.格波是固體物理中典型的集體激發,它代表系統內所有原子在各自的平衡位置附近振動的一種集體模式.在簡諧近似下格波是相互獨立的,聲子是指格波的量子.一個格波,即一種振動模,稱為一個聲子模式.它是晶格原子集體運動狀態的激發單元,因此系統一般狀態可看作是這些獨立的基本激發單元(聲子)的集合.引入聲子概念后,N個原子的耦合振蕩問題在簡諧近似下就被約化為無相互作用的理想聲子氣體來進行理論分析和處理,由此可以很好地解釋晶體熱力學性質的微觀機制.

最早物理學家們以一維單原子鏈為固體材料的簡化模型,在簡諧近似下研究了一維單原子鏈的格波理論及色散關系[5,6].考慮到實際固體往往是非線性的,需加入非線性作用,而非線性作用的出現使得聲子與聲子相互作用,導致色散關系在一般情況下很難解析求解.有些情況溫度比較低時,可將系統的非線性項看作是一個小的微擾,運用標準力矩陣擾動法可以解析得到色散關系[7];而溫度比較高時,小的非線性微擾近似已不再成立.近些年來研究學者們提出了聲子譜能量密度(spectral energy density,SED)方法[8?10]和有效聲子理論(effective phonon theory,EPT)[11?13]來預測非線性系統的色散關系.這兩種方法在高溫下也可以準確地預測非線性系統的色散關系.但值得注意的是,上述預測色散關系的理論大多適用于獨立的固體結構和獨立的晶格鏈模型.但在實際應用中,固體材料往往不是孤立存在的,最常見的為耦合式結構,例如廣泛應用于芯片散熱、航空航天等領域的碳納米管陣列[14?17]和多層石墨烯[18?22]等納米材料.耦合式的結構會導致界面的出現,這時除了非線性導致的聲子與聲子相互作用,還會出現聲子與界面的作用,從而影響到系統的色散關系.目前關于這方面的研究還十分匱乏,因此非常有必要研究耦合系統的格波理論及色散關系.

本文選取耦合Frenkel-Kontorova (FK) 雙鏈模型來研究耦合系統的格波理論.FK 模型是在1938 年由Frenkel 和Kontorovaza[23]兩位物理學家在研究晶體位錯運動時首次提出.此模型形式簡單,是一個置于外部周期勢場中和最近鄰粒子間存在簡諧相互作用的原子鏈模型.它可以很好地描述廣泛的非線性物理現象,例如電荷密度波的傳播、在晶格表面原子吸附層的動力學,以及磁有序結構中的磁疇壁等;在凝聚態物理和統計物理研究中也被廣泛地用來模擬系統的熱傳導及聲子輸運過程.因此我們采用耦合FK 雙鏈模型.本文主要計算了在低溫小振動近似、有限溫、高溫近似情況下耦合FK 雙鏈的格波解及色散關系.具體討論了色散關系曲線的分布情況、頻譜范圍和帶隙結構的影響因素等.并且給出了溫度對耦合FK 雙鏈色散關系的影響規律.研究結果可為分析鏈間界面耦合對晶格的振動特點和物理性質的影響提供理論依據.

2 耦合FK 雙鏈的色散關系

2.1 耦合FK 雙鏈模型

考慮兩條相同的耦合FK 鏈模型(如圖1 所示),選取最簡單的鏈間耦合作用,即鏈1 與鏈2 通過簡諧耦合作用相連接,耦合強度為kc.為計算方便,取兩條FK 鏈的原子質量相同均為m.un,j表示鏈n(n=1,2)中第j個粒子偏離平衡位置的位移.假設每條鏈中相鄰原子之間的平衡距離為a,兩條鏈當中的第j個粒子對為一個原胞,所以原胞的大小為a.

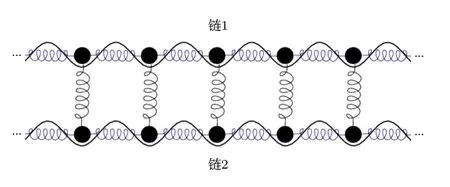
圖1 耦合FK 雙鏈模型示意圖Fig.1.Schematics of the coupled FK chains model.

2.2 低溫近似下耦合FK 雙鏈的色散關系

2.2.1 色散關系計算方法

FK 鏈中相鄰原子間的相互作用力是線性恢復力,設恢復力常數為kn(n=1,2),外勢Un(un,j)?Vsub,n(2π)?2cos(2πun,j),Vsub,n為鏈n的外勢深度.則耦合FK 雙鏈中第j個原胞內兩個原子的運動方程為

(1)式很難解析求解,在低溫情況下,原子的動能較小,其活動范圍主要限制在 FK 鏈外勢的勢阱中.因此,在低溫小振動近似下,耦合系統相應的運動方程可以寫為

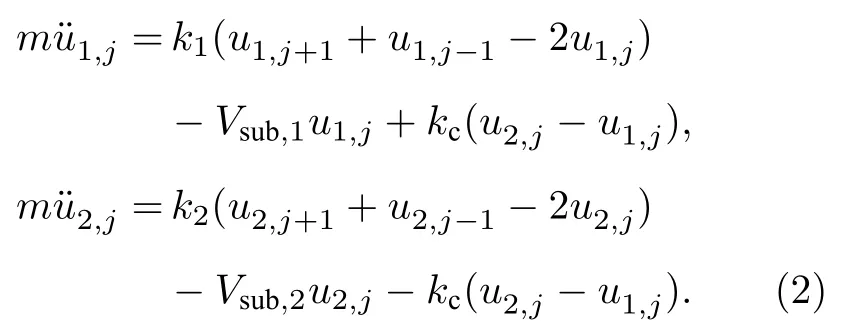
設該方程組有行波解:

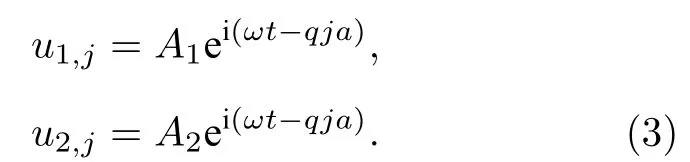
其中,a為每條鏈中相鄰原子之間的平衡距離,ω為頻率,q為波數.將(3)式代入(2)式中可以得到關于振幅A1和A2的方程組:

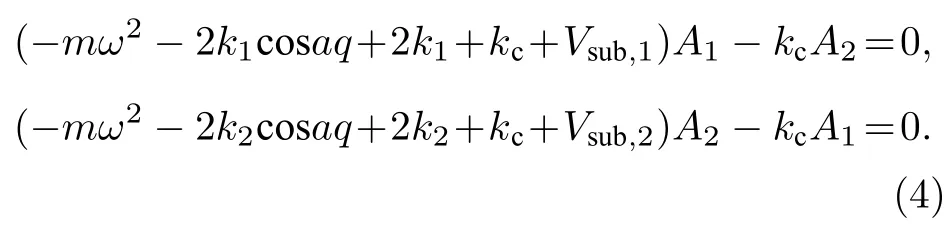
方程組(4)式有非零解的條件是其系數矩陣的行列式等于零,即

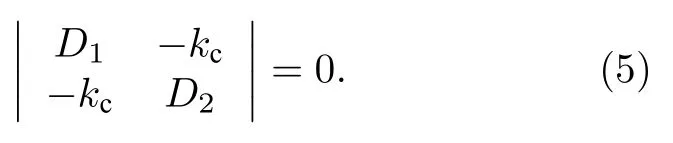
這里令

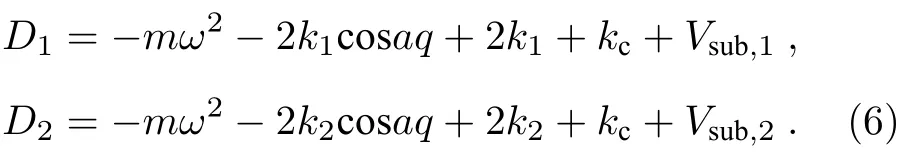
由此可得

這是關于ω2的一元二次方程,取相同的外勢深度并令Vsub,1Vsub,2V求解(7)式可得

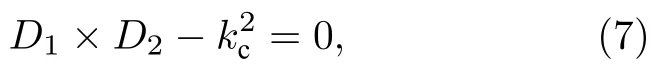
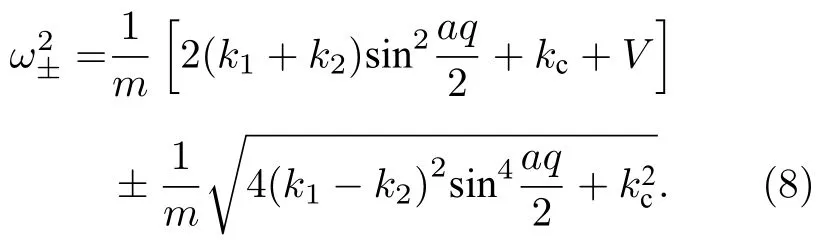
因為兩條FK 鏈相同,所以k1k2,可以得到

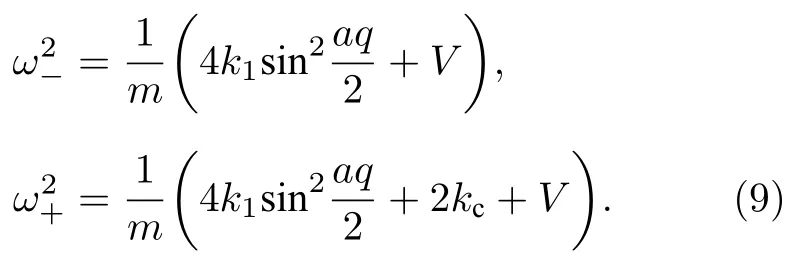
2.2.2 色散關系結果分析

(9)式給出了兩條相同的耦合FK 鏈系統在低溫小振動近似下的色散關系.可以發現聲學波的色散關系(ω?)始終與單條FK 鏈結果[24]完全相同,并不隨鏈間耦合作用而發生變化;而光學波的色散關系(ω+)隨鏈間耦合作用增強向高頻方向移動.這是因為對于聲學支ω?,第j個原胞中的粒子對在做同向運動,運動完全一致,像一個剛體一樣整體地振動,因此對應的色散關系與單條FK 鏈結果完全相同.但值得注意的是這里只是色散關系表現形式與單鏈相同,仍然是兩條鏈所有原子集體運動的結果.對于光學支ω+,第j個原胞中的粒子對在做相對振動,運動完全相反,運動中保持它們的質心不變,對應的光學支會受到鏈間耦合強度的調制.由(9)式的色散關系可以發現,聲學支和光學支的頻譜范圍 Δω?、Δω+和頻率禁帶 Δω′與FK 鏈的恢復力系數、外勢深度以及鏈間耦合強度系數均有關聯.

現對(9)式得到的ω+和ω?進行數值擬合,得色散關系曲線如圖2(k1k21,V1,m1)所示.圖2 呈現了不同鏈間耦合強度kc下的色散關系,可以看到頻率禁帶的存在與否取決于鏈間耦合強度的大小.當鏈間耦合強度較小時,不存在頻率禁帶(見圖2(a)),但光學支位置隨著鏈間耦合強度的增加不斷明顯升高;當鏈間耦合強度增加到某一臨界值后,頻率禁帶將出現(見圖2(b)),并隨著鏈間耦合強度增加,頻隙不斷變大(見圖2(c)).通過以下計算,可以得到頻隙為0 的臨界鏈間耦合強度.令

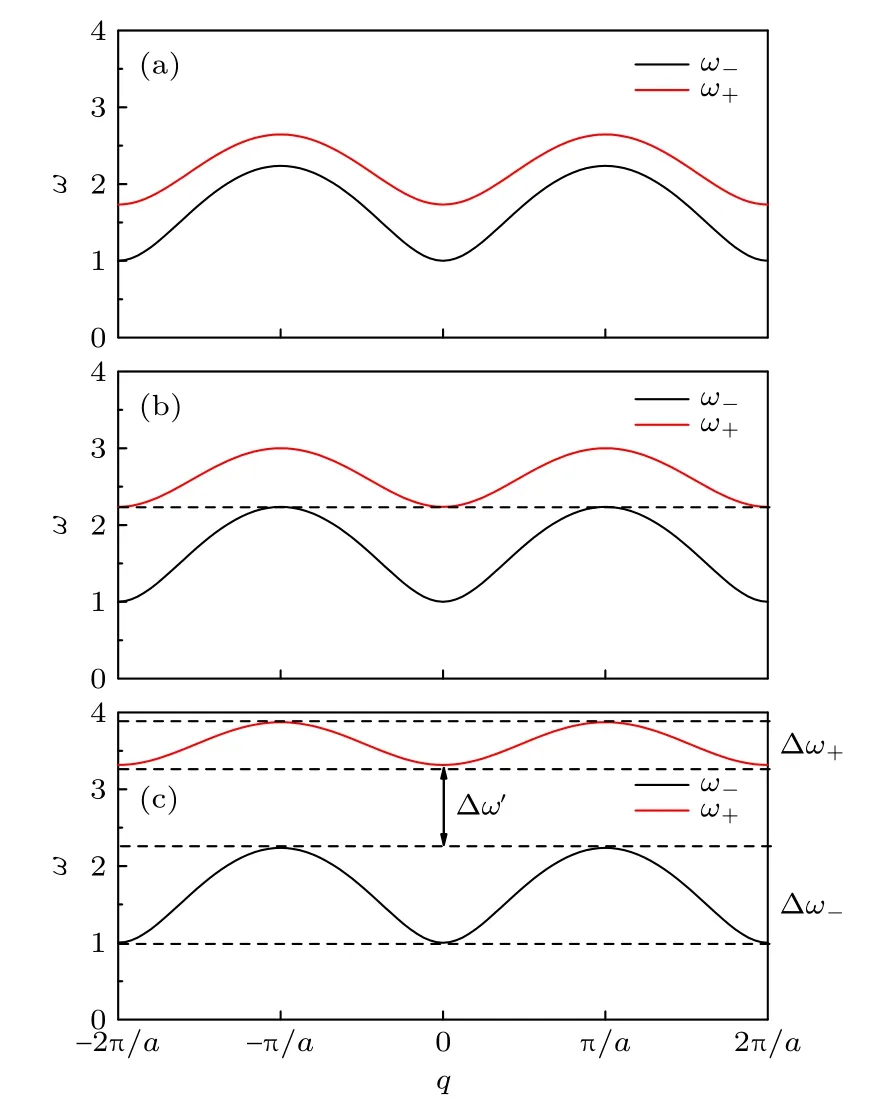
圖2 耦合FK 雙鏈在低溫小振動近似情況下的色散關系(k1 k2 1,V1,m1) (a) kc 1;(b) kc 2 ;(c) kc 5Fig.2.Dispersion relationship of the coupled FK chains under low temperature approximation with small vibration(k1 k2 1,V1,m1):(a) kc 1;(b) kc 2 ;(c) kc 5 .

由(9)式得

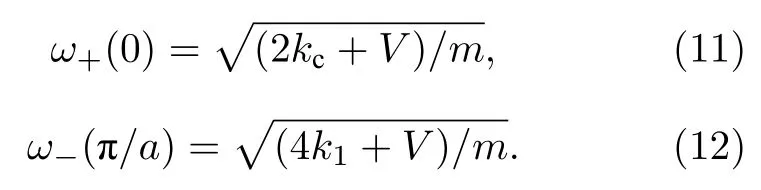
將(11)式和(12)式代入(10)式計算可得

由以上計算結果可知,兩條相同耦合FK 鏈系統在低溫下的臨界鏈間耦合強度為FK 鏈恢復力系數的2 倍,與外勢深度無關.取k1k21,可得臨界鏈間耦合強度kc2,與圖2(b)數值計算結果一致.

2.3 有限溫度下耦合FK 雙鏈的色散關系

2.3.1 色散關系計算方法

第2.2 節考慮的是耦合FK 雙鏈模型在低溫小振動近似下的情況,外勢泰勒展開的高階項可以忽略,而在有限溫度,即溫度并不是很低的情況下,這樣的近似是不合理的.這時需要借助耦合系統的EPT[25]來具體討論耦合FK 雙鏈的色散關系及鏈間耦合對此耦合系統色散關系的影響.

首先給出兩條相同的耦合非線性鏈模型的哈密頓量:

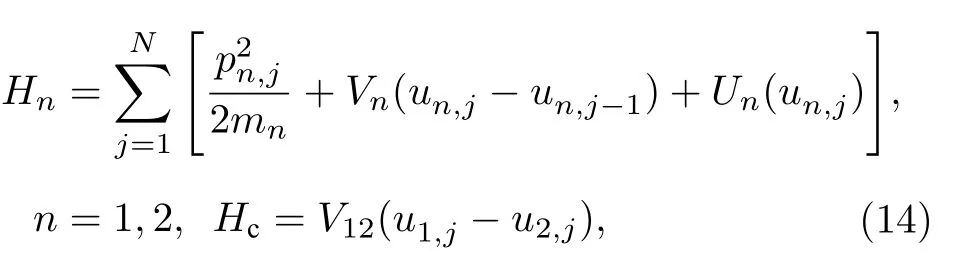
這里H1,H2和Hc分別表示鏈1、鏈2 和耦合項的哈密頓量.un,j仍然表示鏈n(n=1,2)中第j個粒子偏離平衡位置的位移,pn,j是此粒子的動量.N表示鏈長,mn是每條鏈粒子的質量(為方便,設所有的粒子質量mn1).為了不失一般性,鏈內相鄰粒子相互作用勢Vn(un,j ?un,j?1)、外勢Un(un,j)和鏈間相互作用勢V12(u1,j ?u2,j) 的表達式為

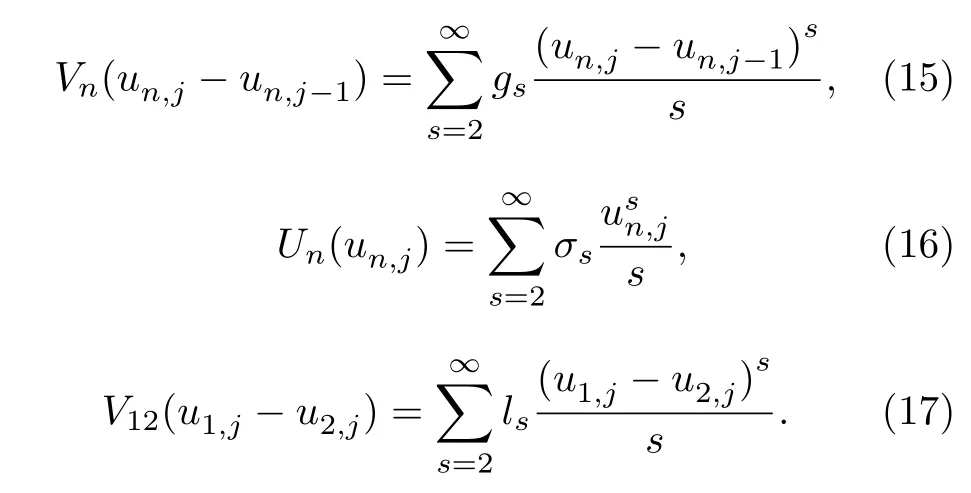
其中,gs為鏈內相鄰粒子相互作用強度,σs為外勢作用強度,ls為鏈間相互作用強度,s2,3,4,···.根據耦合非線性雙鏈的EPT[25],其重整化聲子譜的解析表達式為

其中,ωn,k,+為耦合系統聲子譜的光學支,ωn,k,?為聲學支;ωk2 sin(k/2) 是單條簡諧鏈的聲子譜(這里kaq).重整化的參數αn,γn,+和γn,?為

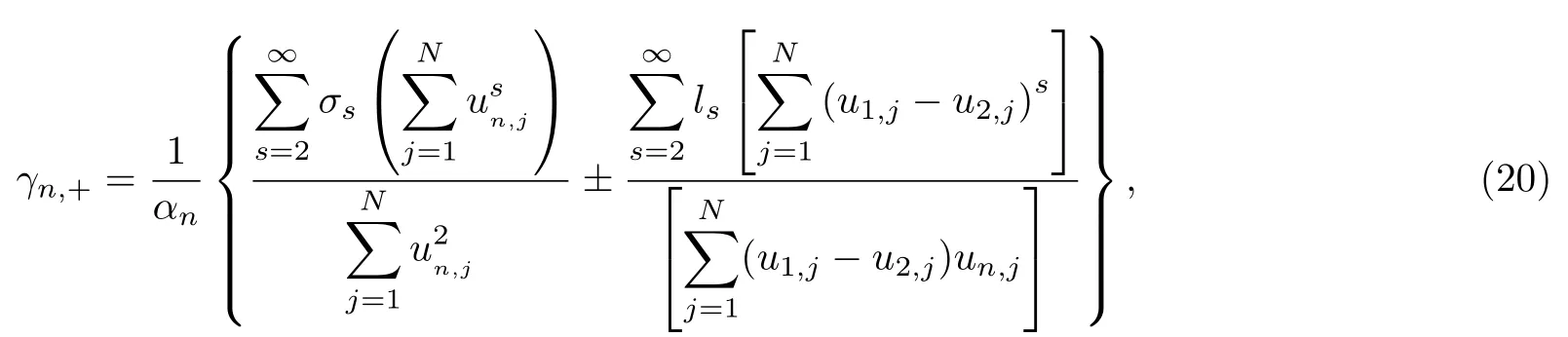
其中,對于鏈1 (n=1) 取“+”,對于鏈2 (n=2)取“–”;

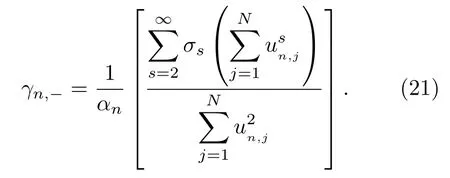
上述理論給出的是一般的兩條相同耦合非線性鏈模型的有效聲子譜.對于兩條相同的耦合FK鏈模型(鏈間耦合作用仍然通過簡諧耦合作用相連接),表達式為

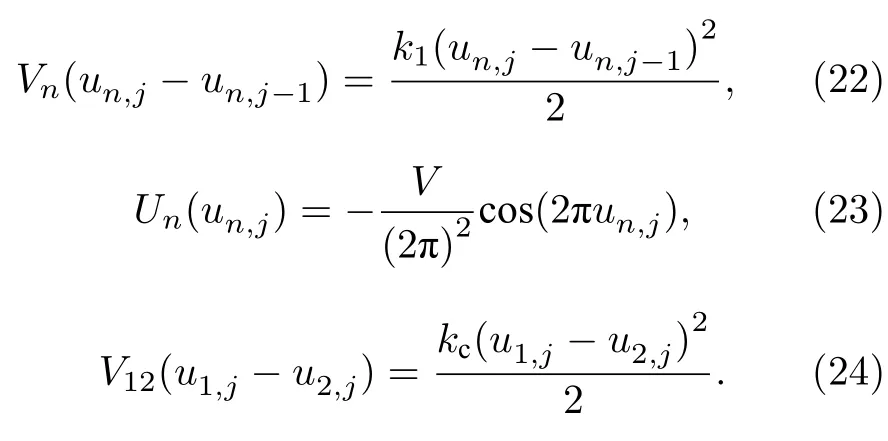
在有限溫度下,粒子在外勢中振動還不太劇烈,振動較小,可以對外勢Un(un,j) 進行泰勒展開,從而得到耦合FK 雙鏈模型的重整化的參數αn,γn,?和γn,+為

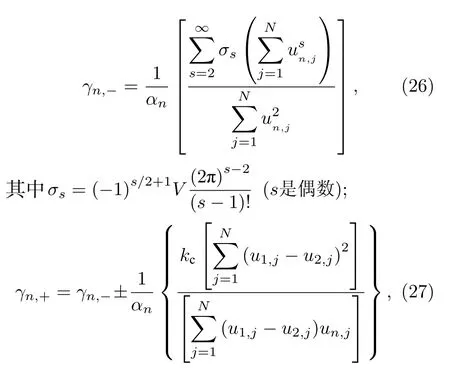
其中,對于鏈1 (n=1) 取“+”,對于鏈2 (n=2)取“–”.

2.3.2 色散關系結果分析

對2.3.1 節的EPT 計算結果進行數值擬合,溫度T=0.05 時的耦合FK 雙鏈(k1k21,V1,m1)的色散關系如圖3 所示,可以看出色散關系和圖2 相比有所下移.這是由于有限溫度下,外勢的高階項作用開始明顯,第3 節會進一步說明溫度對色散關系的影響.同樣圖3 也展示了色散關系隨鏈間耦合作用的變化情況:當鏈間耦合強度較小時,不存在頻率禁帶(見圖3(a));當鏈間耦合強度增加到某一臨界值后,頻率禁帶將出現(見圖3(b)),并隨著鏈間耦合強度增加,頻隙不斷變大(見圖3(c)).通過以下計算,可得到頻隙為0的臨界鏈間耦合強度.令

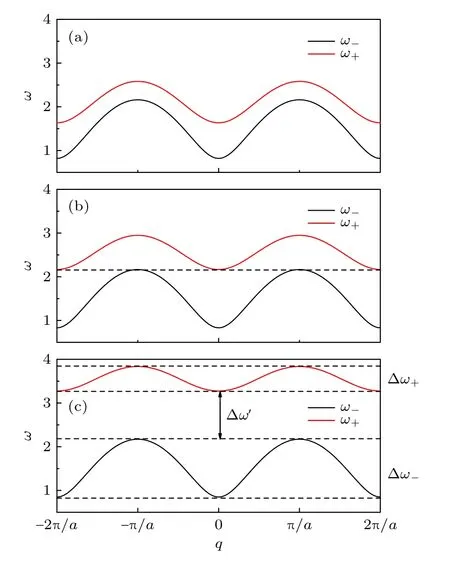
圖3 耦合FK 雙鏈(k1 k2 1,V1,m1)在有限溫度(T=0.05)下的色散關系 (a) kc 1;(b) kc 2 ;(c) kc 5Fig.3.Dispersion relationship of the coupled FK chains(k1 k2 1,V1,m1) under finite temperature(T=0.05):(a) kc 1;(b) kc 2;(c) kc 5 .

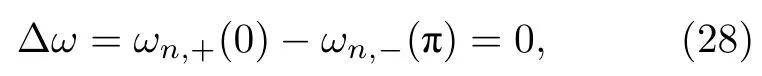
由(18)式結合(25)式—(27)式得

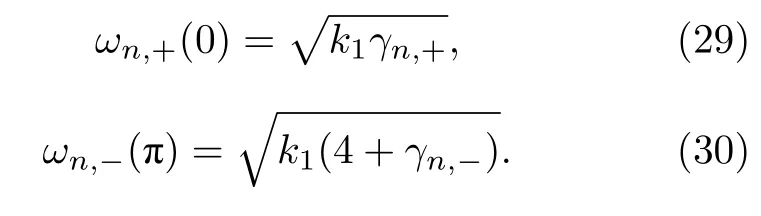
將(29)式和(30)式代入(28)式計算可得

上述計算結果說明對于兩條相同的耦合FK鏈系統,在有限溫度下,臨界鏈間耦合強度仍為FK 鏈恢復力系數的2 倍(圖3(b)數值結果也驗證了這一結論),與外勢深度無關,和低溫小振動近似下的結論相同.

2.4 高溫近似下耦合FK 雙鏈的色散關系

2.4.1 色散關系計算方法

在高溫區域,由于粒子動能很大,會脫離外勢的束縛,這時外勢可以忽略,所以FK 鏈又回歸到了簡諧鏈,兩條相同耦合FK 鏈的色散關系和兩條相耦合簡諧鏈的結果相同(只需令(9)式的外勢深度V=0),即

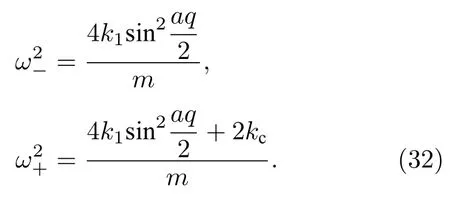
2.4.2 色散關系結果分析

由(32)式可知,高溫情況下頻譜范圍和頻率禁帶僅與FK 鏈的恢復力系數、鏈間耦合強度系數有關聯,與外勢深度無關,這點與低溫及有限溫的情況有所不同.圖4 給出了高溫下耦合FK 雙鏈(k1k21,V1,m1)的色散關系.發現在長波極限下,聲學支頻率為0,光學支也比低溫和有限溫情況有明顯下移,主要由于高溫下粒子運動劇烈,脫離了外勢的約束.此外,從圖4 可以看出,當鏈間耦合強度逐漸增加到某一臨界值后,頻率禁帶出現,并隨著鏈間耦合強度增加,頻隙不斷變大,這在低溫、有限溫的討論中已提到,結論均類似.按照前面類似的計算方法,也可得到頻隙為0 的臨界鏈間耦合強度為kc2k1.結合低溫和有限溫的討論可知:兩條相同的耦合FK 鏈系統,在鏈間耦合作用為簡諧耦合作用時,臨界鏈間耦合強度始終為FK 鏈的恢復力系數的2 倍,即kc2k1,并不受溫度的影響.

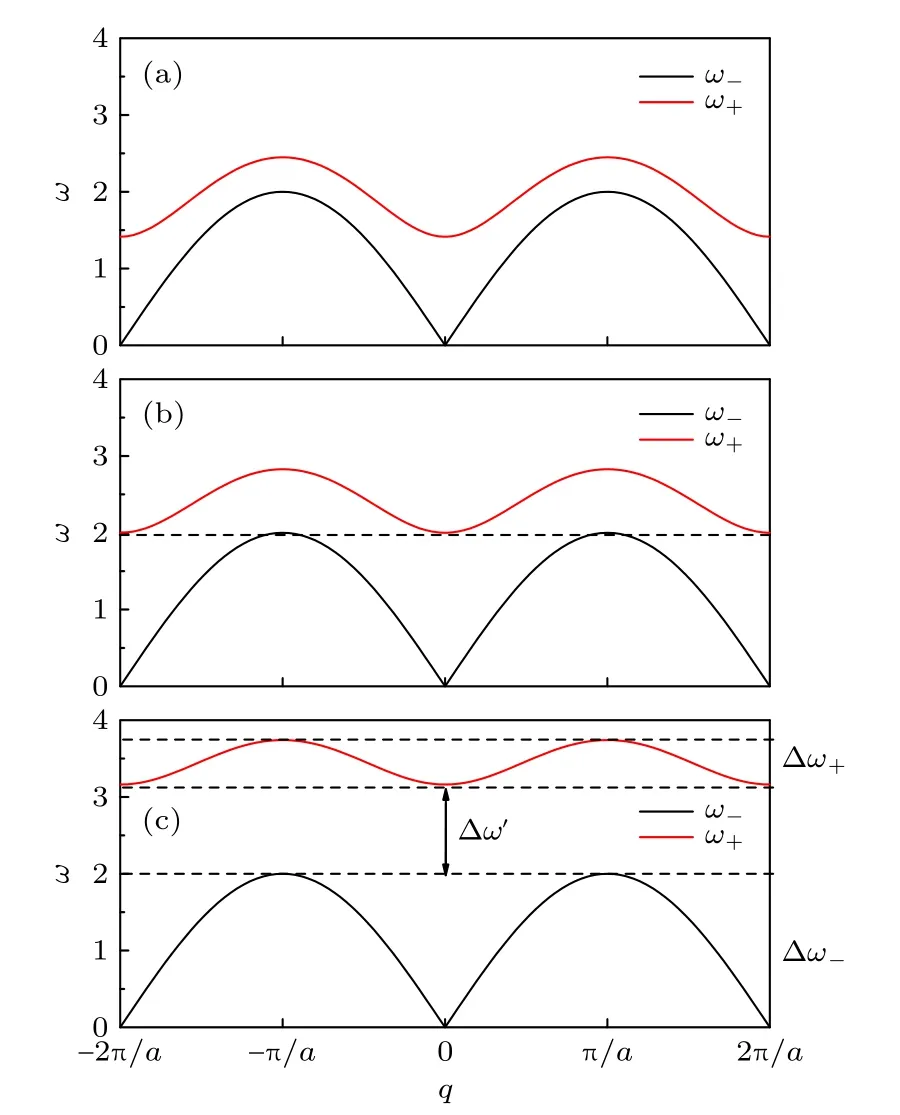
圖4 耦合FK 雙鏈在高溫近似下的色散關系(k1 k2 1,V 1,m1) (a) kc 1;(b) kc 2;(c) kc 5Fig.4.Dispersion relation of coupled FK chains under high temperature approximation (k1 k2 1,V1,m1):(a) kc 1;(b) kc 2;(c) kc 5 .

上述結論表明FK 鏈的恢復力系數越大,所對應臨界鏈間耦合強度越大.換言之,要想使恢復力系數很大的耦合雙鏈出現頻隙結構,鏈間耦合強度必須足夠強.鏈間耦合強度的強弱和很多因素有關,如果耦合固體材料缺乏良好的接觸或表面不是很平整,界面耦合強度系數就會比較弱;如果耦合固體材料能夠彼此很好地接觸,在界面處就可能形成化學鍵,導致界面耦合強度系數會很強.從上述結論發現,通過改變耦合雙鏈的恢復力系數,進而能改變帶隙結構.對帶隙結構的改變和控制可以指導人們設計一定的聲子禁帶和允帶(處于禁帶頻率范圍內的振動將被禁止在晶體中傳播[26,27];處于通帶頻率范圍內的振動會傳遍整個結構),可用于模式選擇、能量傳輸、傳播的指向性等諸多領域,對新型功能材料在工程上的應用很有幫助[28,29].

3 溫度對耦合FK 雙鏈色散關系的影響

第2 節給出了在低溫、有限溫和高溫情況下耦合FK 雙鏈色散關系的解析表達式,并分析了色散關系的分布情況、頻譜范圍和帶隙結構的影響因素等.本節對于相同的耦合FK 雙鏈,固定鏈間耦合強度kc,具體討論溫度對耦合FK 雙鏈色散關系的影響規律.但什么溫度為低溫? 什么溫度為高溫?第2.2 節和第2.4 節的討論只是表明在溫度足夠低和足夠高時,可分別用(9)式和(32)式計算色散關系,但并不明確溫度具體要低于或高于什么值.考慮到EPT 可適用于低溫情況,我們可以用EPT 來計算具體低溫數值下的色散關系,并與低溫小振動近似下的結果對比.而在高溫時,采用SED 方法[8?10]計算具體高溫數值下的色散關系,并與2.4 節高溫解析的結果對比.下面簡單介紹SED 方法[8?10],SED 的表達式為

圖5 展示了耦合FK 雙鏈在kc1.0 時的色散關系隨溫度的變化情況(考慮到SED 的計算時間成本,本文只計算了波數0— π/a(鏈常數a=1)范圍的色散關系,但數據足夠說明問題).圖5 中紅實線和黑實線是EPT 的計算結果;紅色和黑色圓點是在低溫小振動近似下計算的結果;紅色和黑色方框是高溫下計算的解析結果;等高線圖是SED 方法的計算結果.從圖5(a)和圖5(b)可以發現,溫度T低于0.01 時,EPT 計算的色散關系與低溫小振動下的解析結果幾乎無差別,完全吻合.這說明溫度低于0.01 時,就可以用前面低溫小振動近似得到的解析結果去計算色散關系,并且色散關系分布在此低溫區域基本不受溫度影響.當溫度升高,如溫度高于0.01 時(見圖5(c)和圖5(d)),色散關系與圖5(a)和圖5(b)相比有明顯下移,且溫度越高,下移幅度越大.這是由于溫度升高,外勢高階項開始起作用,并且發現聲學支下移幅度較光學支下移幅度大.因此可以推論在鏈間耦合強度足夠大,出現頻隙結構的耦合系統中,溫度升高頻隙會變大.當溫度進一步升高,例如溫度高于0.1 時(見圖5(e)和圖5(f)),色散關系較圖5(c)和圖5(d)有大幅度下移,聲學支在長波極限下頻率幾乎降為0,光學支也有明顯下移.說明在溫度高于0.1 時,外勢對粒子運動影響已經可以忽略,并且SED 的計算結果和前面高溫解析計算的色散關系完全吻合.因此溫度高于0.1 時,就可以用2.4 節高溫解析結果來計算色散關系,并且色散關系分布在高溫區域基本不受溫度影響.

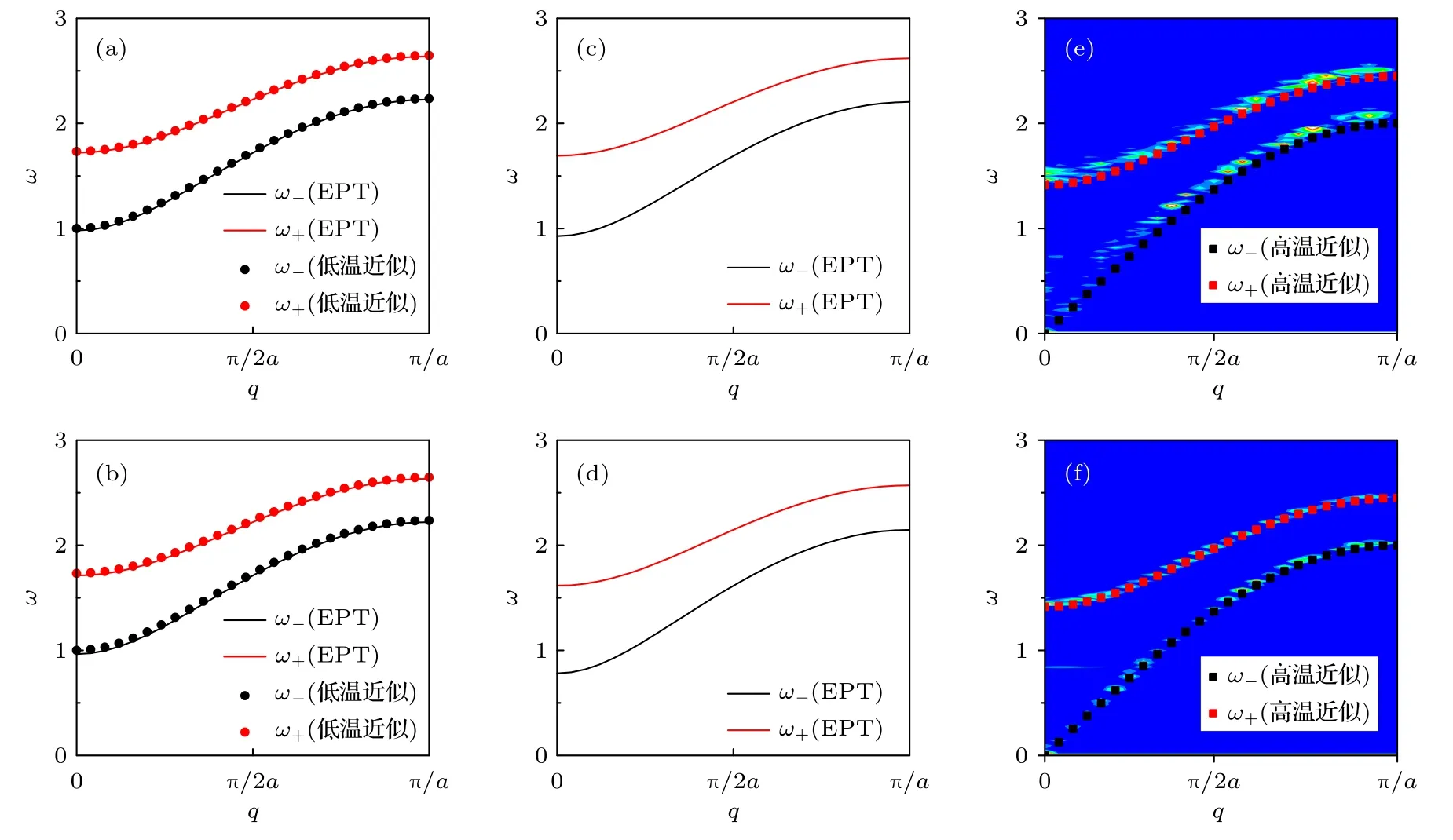
圖5 耦 合FK 雙鏈在不同溫 度下的色散關 系(k1 k2 1,V1,m1 ,kc 1.0) (a) T0.005;(b) T0.01 ;(c) T0.02;(d) T0.06;(e) T0.10;(f) T 0.20Fig.5.Dispersion relation of coupled FK chains at different temperature (k1 k2 1,V1,m1 ,kc 1.0):(a) T0.005 ;(b) T0.01;(c) T0.02;(d) T0.06;(e) T0.10;(f) T0.20 .

4 總結

本文計算了兩條相同的耦合FK 鏈系統在低溫、有限溫和高溫情況下色散關系的解析表達式.研究發現頻譜范圍、頻率禁帶與FK 鏈的恢復力系數、鏈間耦合強度系數均有關聯,低溫和有限溫的情況還與外勢深度有關系.帶隙結構出現的臨界鏈間耦合強度始終為FK 鏈恢復力系數的2 倍,并且不受溫度的影響.進一步研究了給定鏈間耦合強度下溫度對耦合FK 雙鏈色散關系的影響規律.發現溫度在低于0.01 時,色散關系分布基本不受溫度影響;溫度在高于0.01 時,色散關系有明顯下移,且溫度越高,下移幅度越大,直至溫度上升到0.1,聲學支在長波極限下頻率幾乎降為0.至此耦合系統脫離外勢的影響,溫度再升高色散關系分布將不受溫度影響.此外還給出了低溫小振動近似及高溫下解析得到的色散關系的溫度適用范圍.上述研究結果讓我們對鏈間耦合作用和溫度使晶格振動色散關系產生的變化有了具體的認識,有助于拓寬和加深對耦合材料物理性質的了解,可以指導實現設計一定的聲子禁帶和允帶,可用于模式選擇、能量傳輸、傳播的指向性等諸多領域,這對新型功能材料在工程上的應用很有幫助[28,29].此外,鏈間耦合作用的存在及溫度的變化導致系統色散關系的改變可以幫助我們理解很多傳熱現象.例如碳納米管陣列和多層石墨烯等納米材料的熱導率明顯低于單臂碳納米管[30]和單層石墨烯[31]的熱導率;溫度升高使得納米材料熱導率降低等.因此本文研究的結果對于能量輸運、熱調控等實際應用有著重要的指導意義.