菜用大豆莢干燥特性研究

楊旭諸愛士

(1.浙江微松冷鏈科技有限公司，浙江 杭州 311121；2.浙江科技學院生物與化學工程學院，浙江 杭州 310023)

菜用大豆是中國長江流域及西南地區(qū)夏秋季的主要蔬菜之一，菜用大豆莢是在其加工和食用過程中產生的一種生物質，在農村有部分被作為飼料或堆肥等，大量的以加工廢物或廚余垃圾被廢棄，特別是在城市，基本沒有被利用。近年來，這種豐富的生物質資源的利用研究引起了研究者的關注，王純榮等[1]采用添加了表面活性劑的水溶液從大豆豆莢中超聲提取了黃酮；趙麗等[2]采用多種方法從鮮食大豆莢中提取了膳食纖維；Huang等[3]從菜用大豆莢中提取了水溶性纖維；吳潔等[4]采用乙醇水溶液從大豆莢中提取了甾醇；王義英等[5]對大豆莢進行改性將其制成吸附劑，研究了其吸附廢水中的苯酚效果；Lisboa等[6]將大豆莢與桉木復合生產膠合復合材料用于建筑；Kong等[7]利用大豆豆莢制備了低成本大容量超級電容器。由于鮮豆莢含水率高、易腐，不便于儲存，因此在利用豆莢時，需要對豆莢進行處理以便保存，而干燥脫水是保存農產品、生物質材料的常用方法。通過干燥，脫除大部分水分，降低微生物活性，從而保證農產品在儲存期的質量穩(wěn)定[8]。

為了強化干燥過程以保證產品產量、避免環(huán)境因素的影響以確保產品品質，工業(yè)上常采用干燥設備進行生產，常用的干燥設備有烘房、洞道干燥機，其原理是熱風對流干燥，干燥過程中熱量傳遞和質量傳遞同時進行。探索和掌握干燥過程的數學模型和相關的動力學參數，如擴散系數、活化能等，對干燥條件的篩選、干燥器的設計與選用，有很大的益處。薄層干燥模型是目前用來描述農產品干燥過程最常用的模型[9，10]。目前中外文文獻未見報道大豆莢的干燥，本研究以利于菜用大豆豆莢為目的，著重考察了在鼓風干燥箱和洞道干燥機中熱風溫度對大豆莢干燥時間的影響；選用Page、Modified Page、Weibull、Newton、Henderson and Pabis、Logarithmic、Wang and Singh等7個薄層干燥模型對干燥過程進行描述，見表1，用相關的指標進行比較篩選出擬合度相對較高的模型，進一步計算了菜用大豆莢熱風干燥過程的水分有效擴散系數和活化能。

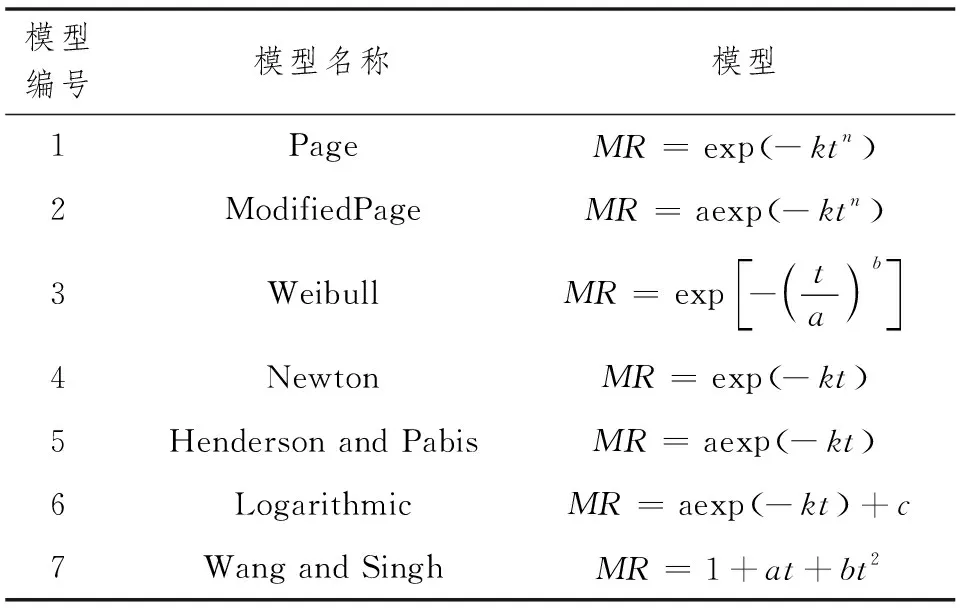
表1 薄層干燥模型

1 材料與方法

1.1 材料、試劑及儀器

1.1.1 材料

新鮮大豆莢，購于杭州農貿市場。

1.1.2 儀器設備

DHG-9123A型電熱恒溫鼓風干燥箱，上海精宏實驗設備有限公司；DG100D數字型洞道干燥裝置，浙江中控科教儀器設備有限公司；T500Y型電子天平，常熟雙杰測試儀器廠。

圖1 鼓風干燥箱

圖2 洞道干燥機

1.2 實驗方法

1.2.1 原料預處理

將新鮮大豆剝去豆留莢，去雜洗凈吸干外表附著水分，裝入塑料包裝袋使樣品含水率達到均衡，備用。采用烘箱法測定了新鮮原料的原始含水率，其值為4.057±0.036kg水/kg絕干物質(濕基為80.2%)。

1.2.2 實驗設計

設定好鼓風干燥箱的溫度，循環(huán)風門全開，此時箱內空氣速度約為0.2m·s-1；固定洞道干燥機的風速為1.30m·s-1，設定好干燥溫度；待溫度達到穩(wěn)定；取樣品20.0g裝盤，分別在干燥箱和洞道干燥機中進行干燥實驗，考察不同干燥溫度對干燥的影響；每隔一定時間記錄樣品質量和干燥時間，實驗至樣品質量保持3min不變時結束；完成數據處理與計算。

1.3 結果表達

1.3.1 干燥參數

試樣的瞬間干基含水率Xt、瞬間水分比MRt分別按公式(1)、公式(2)計算。

(1)

式中，Xt為t時刻試樣的干基含水率，kg水/kg絕干物質；mi為t時刻的試樣質量，g；mg為絕干時試樣的質量，g。

(2)

式中，MRt為t時刻試樣的水分比，無因次；X*為試樣達到干燥平衡時的干基含水率(干燥結束時)，kg水/kg絕干物質；X0為試樣的原始干基含水率，kg水/kg絕干物質。

1.3.2 模型檢驗指標

薄層干燥模型與實驗數據間的擬合優(yōu)劣采用決定系數R2、卡方χ2和均方根誤差RMSE等3個參數來評估。R2直接取自于擬合圖線，χ2和RMSE分別按公式(3)、公式(4)計算。

(3)

(4)

式中，MRexp，i為實驗測得的瞬間水分比，無因次；MRpre，i為模型預測得到的相應瞬間水分比，無因次；N為實驗觀測數；z為模型中常數數量。

模型的R2越大、χ2和RMSE值越小，則該薄層干燥模型與實驗數據的擬合度越高。

1.3.3 擴散系數與活化能

實驗中測得干燥時間和試樣的干基含水率，由費克第二擴散定律來計算干燥過程中水分的有效擴散系數Deff(m2·s-1)[11，12]，表達式：

(5)

當試樣形狀近似為平板、試樣中原始水分均勻分布、不考慮水分傳遞的外部阻力、干燥過程水分有效擴散系數保持不變、忽略干燥過程中試樣的收縮，對在維度上長和寬比厚要大得多的片狀樣品，公式(5)可簡化為水分沿厚度方向的一維擴散，其解見公式(6)[12]。

(6)

式中，N為正整數；H為水分傳遞的距離，m；t為干燥時間，s。

大豆莢試樣基本符合上述條件，即可用公式(6)計算。因裝載試樣的盤面有孔，且試樣間有縫隙，干燥時豆莢試樣的內外表面均能與熱風接觸，故公式(6)中H取試樣厚度的1/2。當干燥時間較長時，公式(6)可只取第1項，即公式(7)[11，12]。

(7)

對公式(7)左右兩邊均取對數，可得公式(8)。

(8)

作lnMR～t圖，對實驗點進行線性擬合，所得直線斜率即為-π2Deff/4H2，經計算可得到水分的有效擴散系數Deff。

干燥溫度與水分有效擴散系數可用阿累尼烏斯方程關聯(lián)，從而可計算得到干燥過程的活化能Ea，見公式(9)[11]。

(9)

式中，D0為方程常數，m2·s-1；Ea為干燥活化能，J·mol-1；R為氣體常數，8.314J·mol-1·K-1；T為干燥溫度，℃。

對公式(9)左右兩邊均取對數，得公式(10)。

(10)

作lnDeff～1/(T+273.15)圖，對實驗點進行線性擬合，即可由直線截距和斜率計算得到D0和Ea。

2 結果與討論

2.1 溫度對干燥的影響

整個大豆莢，在1.2.2所述條件下，分別在鼓風干燥箱和洞道干燥機中測定了干燥溫度為50℃、60℃、70℃、80℃和90℃時試樣的質量和干燥時間數據，經計算和繪圖，得到試樣瞬間水分比與干燥時間關系即MR～t圖，見圖3。

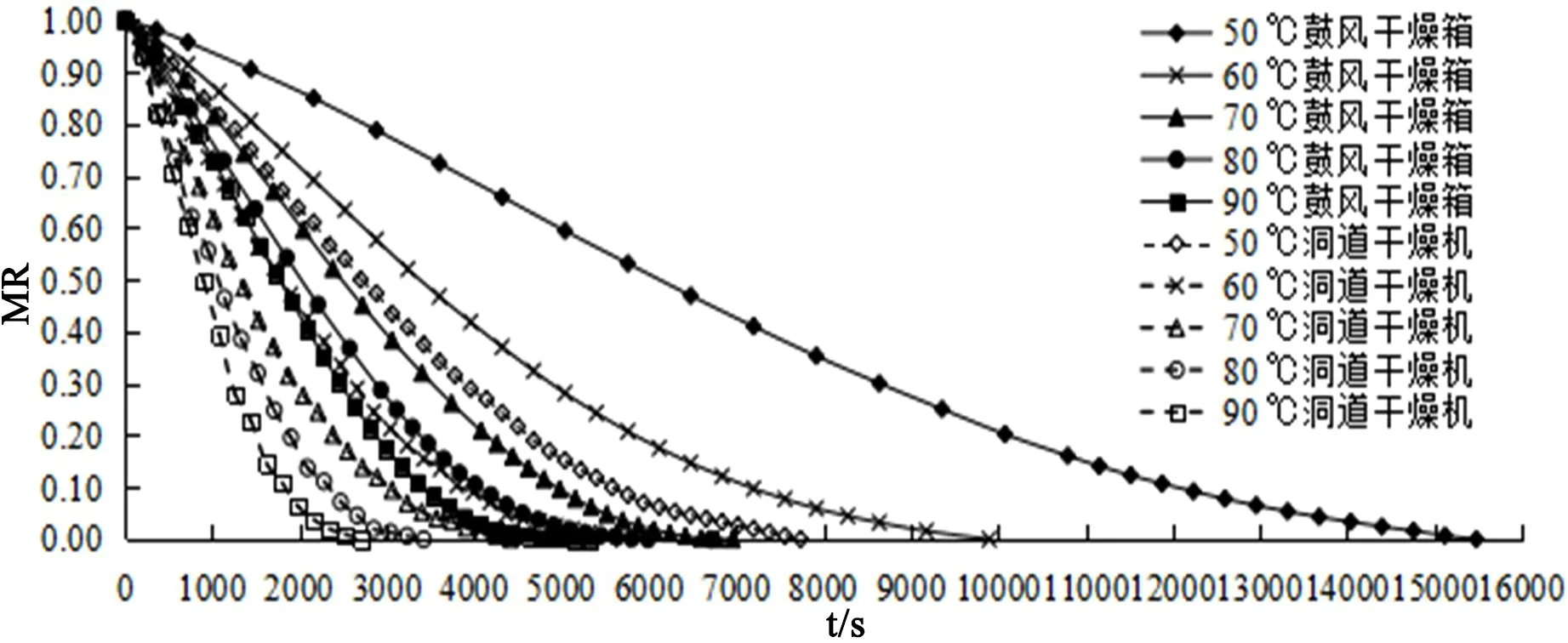
圖3 試樣在不同干燥裝置中不同干燥溫度的MR～t關系

圖3顯示，干燥溫度對試樣水分比有顯著的影響，不同裝置中不同干燥溫度下，試樣水分比的變化基本上是先快速減小，然后變緩慢，直至平衡；水分比減小速度隨干燥溫度增高而加快。這是由于干燥介質的溫度越高，傳熱溫差越大，相對濕度越小，水分子熱運動越強；既使傳熱推動力增大，又使傳質推動力加大，水分子擴散速度亦加快，同時促進了傳熱和傳質。同時可看到，鼓風干燥箱干燥效果不如洞道干燥機，其原因是洞道干燥機中熱風的速度大得多，風速大，對流強，傳熱系數與傳質系數均會提高，從而可提高干燥速度、減少干燥時間。

2.2 模型與評價

用所選模型擬合MR和t數據，將所得模型參數和評估指標值匯總，鼓風干燥箱干燥的值見表2，洞道干燥機干燥的值見表3。

從表2可以看到，R2值在0.6019～0.9971之間變化，χ2值在0.000208～0.312499間波動，RMSE值最小0.013523、最大0.538682，平均R2值Wang and Singh模型最大、Modified Page模型次之，而平均χ2和RMSE值均是Modified Page模型最小，因此對大豆莢在鼓風干燥箱內干燥，Modified Page模型與實驗數據的擬合度最佳，故其能較好地用來描述大豆莢的干燥過程。

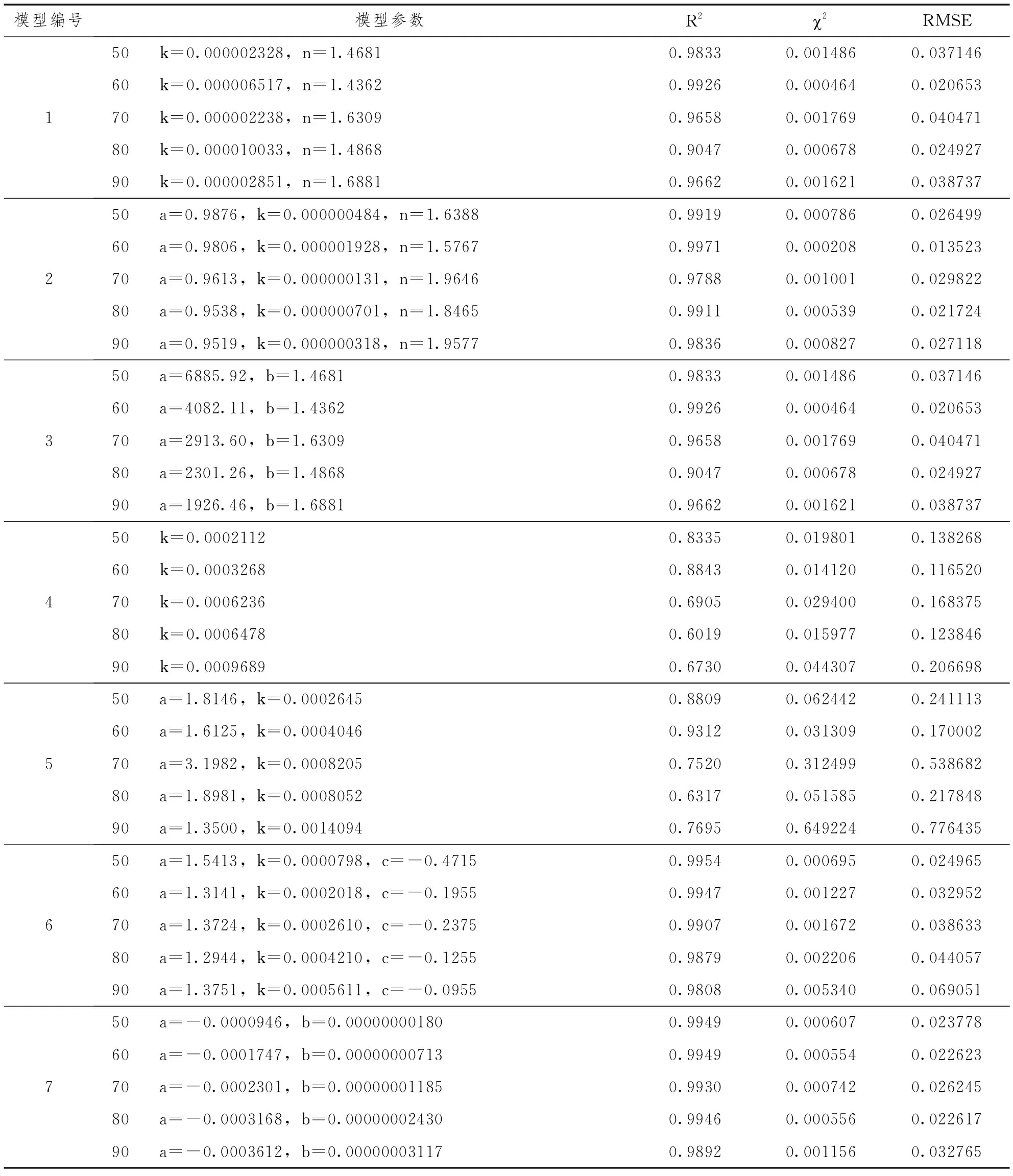
表2 鼓風干燥箱不同干燥溫度下的模型參數和評估指標

從表3可以看到，R2值在0.8612～0.9977之間變化，χ2值在0.000253～0.087961間波動，RMSE值最小0.002270、最大0.306992，平均R2值也是Wang and Singh模型最大、Modified Page模型次之，而平均χ2和RMSE值也均是Modified Page模型最小，因此對大豆莢在洞道干燥機內干燥，Modified Page模型與實驗數據的的擬合度最佳，故其能較好地用來描述大豆莢的干燥過程。

表3 洞道干燥機不同干燥溫度下的模型參數和評估指標

2.3 有效擴散系數Deff與活化能Ea

將各裝置各溫度下的實驗數據代入公式(8)處理，并繪圖計算得到Deff值，并將其匯總于表4。

表4數據顯示，水分有效擴散系數數Deff值均在DOYMAZ i[12]，Chong C H等[13]文章所報道的范圍內；Deff值隨干燥溫度T的升高而增大，原因是試樣溫度隨熱風溫度升高而升高，促使水分子熱運動增強、分子擴散加快。按公式(10)將表4中的數據處理并繪制lnDeff～1/(T+273.15)關系圖，具體見圖4。

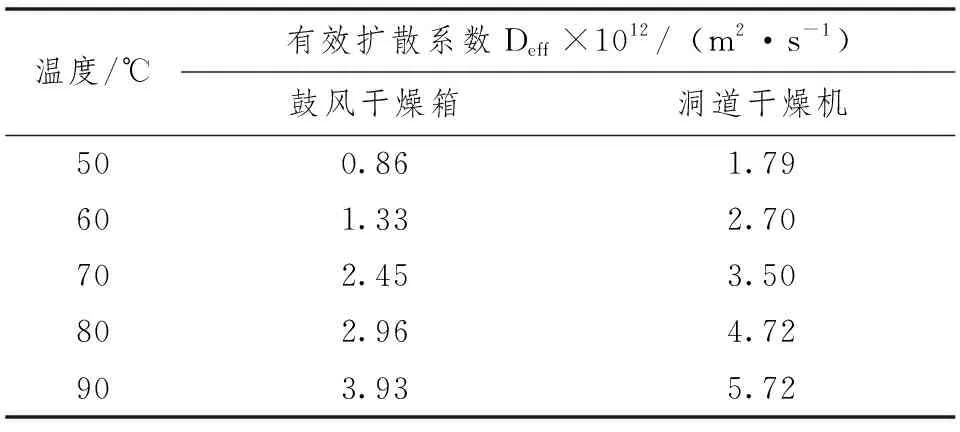
表4 不同溫度下的有效擴散系數

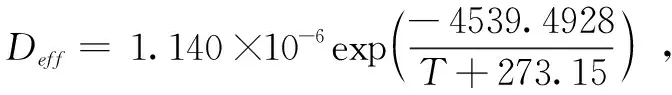
圖4 lnDeff～1/(T+273.15)關系

3 結論

大豆莢無論在鼓風干燥箱還是在洞道干燥機中進行熱風對流干燥時，隨干燥溫度升高試樣的水分比降低而加快，干燥所需時間就越少。經模型指標評估，Modified Page模型是最適宜用來表征大豆莢干燥過程。在實驗條件下，隨干燥溫度升高，水分有效擴散系數Deff增大，數值在0.86×10-12～5.72×10-12m2·s-1，在文獻報道的范圍內；干燥過程的活化能Ea分別為鼓風干燥箱37.74kJ·mol-1、洞道干燥機28.19kJ·mol-1；干燥溫度會對干燥過程有顯著影響。