含參數分數階微分方程邊值問題的極值解
吳怡敏, 沈欽銳
(閩南師范大學數學與統計學院, 福建 漳州 363000)
單調迭代結合上下解的方法已經成為研究微分方程特別是整數階常微分方程邊值問題的極值解存在性的一個有力工具.文獻[1]中考慮了一類帶參數的微分方程邊值問題:

但是對于分數階脈沖微分方程,利用單調迭代結合上下解方法研究其極值解的文獻還是比較少.故為了更好地發展單調迭代方法,本文將分數階的微分方程通過分數階微積分理論轉化為一階常微分方程,然后利用一些解的比較結果得出了該分數階微分方程的極值解的存在性.
本文考慮了如下一類帶參數的分數階脈沖泛函微分方程邊值問題的極值解的存在性:
(1)

1 預備知識
引理1[1]函數f:J′→R的α>0階Rieman-Liouille積分是指
引理2[1]對于Caputo型分數階微分方程,當t∈(tk,tk+1],k=1,2,…,m時有
u(t)+c0+c1(t-tk)+…+cn-1(t-tk)n-1,
ci∈R,i=1,2,…,n,
其中,n=[α]+1.
考慮如下形式的線性微分方程
(2)


2 主要結果

(3)
定理21)稱(x,λ)是(3)的一個下解,如果(x,λ)∈PC1[J,R]×R且滿足
2)稱(y,β)是(3)的一個上解,如果(y,β)∈PC1[J,R]×R且滿足
引理3[2]假設u(t)∈PC1[J,R],p,q∈PC[J,R],dk≥0,bk∈R,使得
成立,則
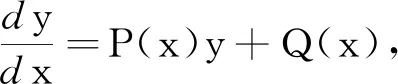
定理3若邊值問題(3)的上解和下解分別是(v0(t),β0)、(u0(t),λ0),其中u0(t)、v0(t)是具有階數為α的連續分數階導數,并且有(v0(t),β0)≥(u0(t),λ0),t∈[-τ,T].假設下列條件成立:
(H1)對于任意的(x1,λ1),(x2,λ2)∈PC′[J×R,R],如果x1 -M(x-y)-N(xt-yt); 則問題(3)在序區間[u0,v0]×[λ0,β0]上有極大解和極小解.其中 [u0,v0]×[λ0,β0]={u∈PC[J,R]: u0≤u≤v0,λ∈R,λ0≤λ≤β,t∈[-τ,T]}. 證明若存在(u(t),λ)∈[u0,v0]×[λ0,β0]滿足問題(3),則對任意(η,s)∈[u0,v0]×[λ0,β0],線性方程的初值問題 (4) 存在且有唯一解表示為 (5) G(η(T),s)-l(λ-s)=0有 (6) 證明當t∈[0,t1]時,由引理2得 由u(0)=k0,得c1=k0.所以當t∈[0,t1]時, 當t∈(t1,t2]時,由引理2得 由Δu(tk)=Ik(η(tk),s)-Lk[u(tk)-η(tk)]得 c2=I1(η(t1),s)-L1[u(t1)-η(t1)]+ 所以當t∈(t1,t2]時, 當t∈(tk,tk+1]時, 綜上,(5)為問題(4)的解.下證唯一性. 先假設下列條件成立: (A1) 存在常數k1>0,k2>0使得不等式成立, 定義算子Φ:E→E,再令(5)式右邊為Φu(t),則證明問題(4)解的唯一性轉化為證明Φu(t)具有不動點,即Φu(t)=u(t). 令w(·):[-τ,0]→R,定義如下函數, (6) 等價.定義算子T:L1[J,R]→L1[J,R], (7) 由此算子Φ有不動點就轉化為算子T有不動點. 對?(z1,λ1)、(z2,λ2)∈L1[J,R]×R,t∈[0,T],當t∈[0,t1]時, |(Tz1)(t)-(Tz2)(t)|= 當t∈(tk,tk+1]時, |(Tz1)(t)-(Tz2)(t)|= 由(A2)知T是壓縮映射算子,(7)有不動點,故(4)有唯一解. 定義算子A:[u0,v0]×[λ0,β0]→PC′[J,R]×R為A(η,s)=(u,λ),其中u,λ分別由(5)、(6)給出,若滿足|f(tk,v(tk),β,vtk)-f(tk,u(tk),β,utk)|=Q(tk),則算子A有下述性質: 1) (u0,λ0)≤A(u0,λ0),A(v0,β0)≤(v0,β0); 2)A在[u0,v0]×[λ0,β0]上不減,即若(η1,s1)≤(η2,s2),則有A(η1,s1)≤A(η2,s2). 下證1),令(u1,λ1)=A(u0,λ0),p=u0-u1,則 p′(t)=u′0-u′1≤f(t,u0,λ0,u0t)+ f(t,u0,λ0,u0t)+M(u1(t)-u0(t))+ f(tk,u1(tk),λ1,u1tk)≤M(u1(t)-u0(t))+ N(u1t-u0t)+Q(tk)= -Mp(t)+N(u1t-u0t)+Q(tk),t∈J′, Δp(tk)=Δu0(tk)-Δu1(tk)≤ Ik(u0(tk),λ0)-Ik(u0(tk),λ0)+ Lk[u1(tk)-u0(tk)]=-Lkp(tk),k=1,2,…,m, p(0)=u0(0)-u1(0)≤0;p(t)=0,t∈[-τ,0]. 由引理1知p(t)≤0(t∈[-τ,T])成立. ①當p(t)<0時,u0 綜上可得(u0,λ0)≤A(u0,λ0);同理可證A(v0,β0)≤(v0,β0). 下證2),記(ui,λi)=A(ηi,si),i=1,2.令p=u1-u2,則由(5)知 p′(t)=u′1-u′2=f(t,η1,s1,η1t)- f(tk,u1(tk),λ1,u1tk)-f(t,η2,s2,η2t)-M(u2(t)- f(tk,u2(tk),λ2,u2tk)≤M(η2-η1)+ N(η2t-η1t)-M(u1(t)-u2(t))+M(η1(t)-η2(t))-N(u1t-u2t)+N(η1t-η2t)+Q(tk)≤ -Mp+N(u2t-u1t)+Q(tk),Δp(tk)=Δu1(tk)- Δu2(tk)=Ik(η1(tk),s1)-Lk[u1(tk)-η1(tk)]-Ik(η2(tk),s2)+Lk[u2(tk)-η2(tk)]≤-Lkp(tk), p(0)=u1(0)-u2(0)=k0-k0=0, p(t)=0,t∈[-τ,0]. 由引理1得p(t)≤0,t∈[-τ,T]. ①當p(t)<0時,u1 ②當p(t)=0時,u1=u2,由0=G(η1(T),s1)-l(λ1-s1)-G(η2(T),s2)+l(λ2-s2)≤-l(λ1-λ2),知λ1≤λ2. 綜上A(η1,s1)≤A(η2,s2). 利用上述類似討論,使用歸納的方法得到一個關于問題(3)上下解序列{un(t),λn}、{vn(t),βn}并且(un+1,λn+1)=A(un,λn)、(vn+1,βn+1)=A(vn,βn),n=0,1,2….則由1),2)得(u0,λ0)≤(u1,λ1)≤…≤(un,λn)≤…≤(vn,βn)≤…≤(v1,β1)≤(v0,β0),并且由(4)、(5)、(6)知上述上下解序列具有如下定義: (8) (9) 且易知(8)、(9)的解為: 由于序列{un(t),λn}單調不減有上界,序列{vn(t),βn}單調不增有下界,可得序列{un(t),λn}、{vn(t),βn}分別在[0,T]上一致收斂,記 由f、G的連續性及(8)、(9)知當n→∞時,(u,λ),(v,β)都是問題(3)的解.下證(u,λ),(v,β)分別是問題(3)的極小解和極大解.令(η,s)∈[u0,v0]×[λ0,β0]是問題(3)的任一解.要證 (u,λ)≤(η,s)≤(v,β),t∈[0,T], 首先(u0,λ0)≤(η,s)≤(v0,β0)對任意t成立.假設對于n∈N,式(un,λn)≤(η,s)≤(vn,βn)成立. 令x(t)=un+1-η,由(8)和(3), x′(t)=u′n+1-η′=f(t,un,λn,unt)- f(tk,un+1(tk),λn+1,un+1,tk)-f(t,η,s,ηt)- M(η-un)+N(ηt-unt)-M(un+1-un)- N(un+1,t-unt)+Q(tk)= -Mx(t)+N(ηt-un+1,t)+Q(tk), Δx(tk)=Δun+1(tk)-Δη(tk)=Ik(un(tk),λn)-Lk[un+1(tk)-un(tk)]-Ik(η(tk),s)≤Lk[η(tk)-un(tk)]-Lk[un+1(tk)-un(tk)]=-Lkx(tk),k=1,2,…,m, x(0)=un+1(0)-η(0)=0; x(t)=0,t∈[-τ,0], 由引理1得x(t)≤0,t∈[-τ,T]. ①當x(t)<0時,un+1<η,則(un+1,λn+1)<(η,s)成立. ②當x(t)=0時,un+1=η,由 0=G(un(T),λn)-l(λn+1-λn)-G(η(T),s)≤-l(λn+1-s), 知λn+1≤s.綜上(un+1,λn+1)≤(η,s)成立.同理可證(η,s)≤(vn+1,βn+1),故有(un+1,λn+1)≤(η,s)≤(vn+1,βn+1),再由數學歸納法可知(un,λn)≤(η,s)≤(vn,βn)對任意的n∈N都成立.令n→∞得(u,λ)≤(η,s)≤(v,β),t∈[0,T].因此,問題(3)在[u0,v0]×[λ0,β0]上有極大解(v,β)和極小解(u,λ),即問題(1)在[u0,v0]×[λ0,β0]上有極大解(v,β)和極小解(u,λ),證畢. 例1考慮如下含參數分數階微分方程邊值問題: (10) 易知(10)等價于 (11) f(t,v,λv,vt)-f(t,u,λu,ut)= λvv-λuu-sint(vt-ut)≥ λu(v-u)-sin 1(vt-ut),
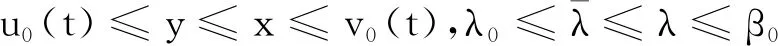
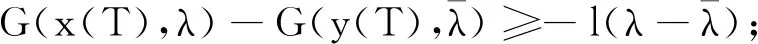
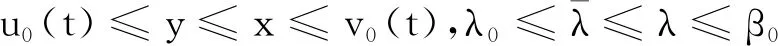






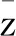



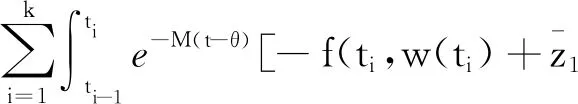
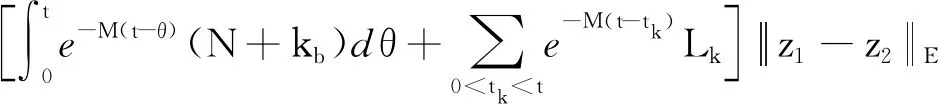

3 實例