統一坐標法巧解直線運動的追擊相遇問題

張祥贊，周 勛

貴州師范大學物理與電子科學學院，貴陽 550025

直線運動的追擊相遇問題是以生活情景為原型，通過抽象加工處理的一類物理模型。該模型的情境性和綜合性較強，對學生的空間想象能力、推理分析能力以及抽象思維能力都提出了較高的要求，是教學的重點、學習的難點。此類問題的研究對象一般為兩個物體，加速度恒定不變，是勻變速直線運動規律的情景化應用。水平直線運動的追擊相遇問題是該類問題的一般表現形式，針對該類問題的變式有多質點做豎直上拋運動的追擊相遇問題和在斜面上運動的追擊相遇問題等。

1 當前解決此類問題的主要方法及弊端

（1）物理分析法。此方法過程詳細，邏輯嚴謹，但對于復雜的運動過程列式繁瑣，求解過程中需要細心認真以及嚴密的邏輯思維，某一環節的出錯將會導致最終結果錯誤。

（2）圖像法。圖像雖可直觀、清晰地表現物體的運動情況，正確畫出圖像后問題就可迎刃而解，但作圖考究、繁瑣，不規范的作圖會對問題的求解產生影響，此外作圖需要較多時間才能完成。

（3）數學函數法。利用兩物體間的距離s與時間t的函數關系s=at+bt+c進行求解。此法是數理結合的典型代表，需要將數理方法融會貫通，對數理思維的要求相對較高。該法中間過程繁瑣，數理分析相對復雜。

（4）相對運動法。運動和靜止具有相對性，合理地選取參考系，會使問題得到簡化。相對運動的分析對于邏輯思維要求相對較高，在求解過程中如不能明確物體的相對運動過程及位置關系，將會導致結果出錯。

上述是以往解決直線追擊相遇問題的常用方法及其弊端，此類求解方法皆是利用質點的位移與時間間隔的函數關系進行求解，需對每一質點的運動逐一討論，面對復雜的多運動過程，列式繁瑣，對于不同質點運動的時間和空間沒有統一，這也是此類方法最大的弊端。

2 統一坐標法原理的界定

采用一維坐標系Ox描述質點的直線運動，使坐標軸原點與參考系的參考點重合，坐標軸與質點軌跡重合，則做直線運動質點的位置矢量為

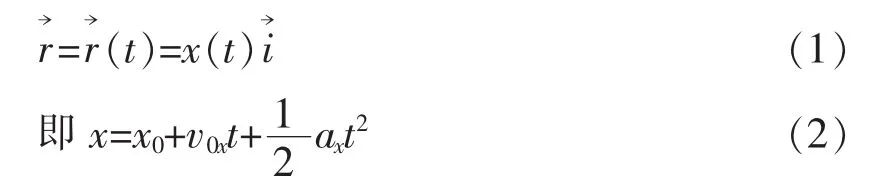
由此可看出，質點的位置矢量隨時間變化的過程中位置坐標是時間的函數，位置矢量的矢端與位置坐標相對應。

與此同時，規定某一質點開始運動的時刻作為計時起點。由于時間的流向是單向的，計時起點的規定就相當于時間坐標軸的建立，從而建立了時空坐標系，將時間與空間進行了統一。該時空坐標不僅僅適用于質點的整個運動過程，還適用于不同質點的運動過程，用同一時空坐標即可描述不同質點的運動情況。因此，將該方法稱為“統一坐標法”。

3 統一坐標法在直線運動中的應用

在質點做直線運動過程中建立時空的統一坐標描述質點的運動，兩質點A、B的時空坐標可分別表示為（x，t）（x，t），若兩質點相遇，則意味著兩質點在同一時刻處在同一空間位置，即x=x、t=t，這就是追擊相遇的條件。現用該法求解直線運動的追擊相遇案例。

例1（2017·南昌模擬）如圖1所示，直線MN表示一條平直公路，甲、乙兩輛汽車原來停在A、B兩處，A、B間的距離為85 m，現甲車先開始向右做勻加速直線運動，加速度a=2.5 m/s，甲車運動6s時，乙車立即開始向右做勻加速直線運動，加速度 a=5.0 m/s，求：（1）乙車運動多長時間被甲車追上；（2）兩輛汽車相遇處距A處的距離。

圖1 兩汽車在平直的公路上運動

以甲車的起點A為原點，建立Ox坐標系，取沿平直公路向右為正，如圖2所示。

圖2 建立水平Ox坐標系

以乙車開始向右運動的時刻為計時起點。設甲車為質點1，乙車為質點2，兩車均做勻變速運動，其中 a=2.5 m/s，a=5.0 m/s。質點 1 的初始條件為 t =-t=-6 s時，x=0，v=0，其運動學方程為

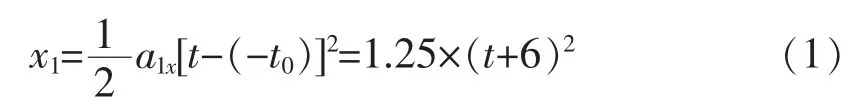
質點2的初始條件為t=0時，x=85 m，v=0，其運動學方程為

若兩物體相遇，則相遇條件為

設相遇時刻為 t ＇，則 1 .25×（t'+6）=85+2.5t'

求得相遇時刻：t＇=4 s，t＇＇=8 s

兩時刻均有意義，說明兩車相遇兩次。t＇=4 s時，質點1追上質點2相遇（甲車追上乙車），t＇＇=8 s，質點2追上質點1再次相遇（乙車追上甲車）。

第一次相遇點距A處的距離

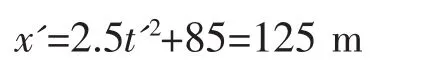
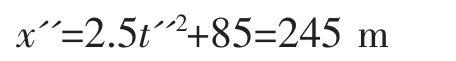
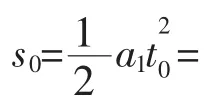
關于坐標原點和計時起點的選取問題。①在選取坐標原點時盡量讓所有質點都落在坐標系的正半軸上，質點在坐標系的負半軸上雖可求解，但引入負號會使計算變復雜。②兩質點初始運動時刻不同步時選擇運動滯后的質點開始運動時刻作為計時起點，方便討論求解；如果選取先運動質點開始運動時刻作為計時起點，則滯后運動的質點在前一段時間間隔內處于靜止狀態，那么需要采用分段函數的方式進行討論，將使得問題的求解更加復雜，也未能體現本法的簡便性。③可選取一個質點的初始位置作為坐標原點和該質點開始運動時刻作為計時起點，也可選取一個質點的位置作為坐標原點，另一質點開始運動的時刻作為計時起點。

在該例題中，選取甲車的初始位置A處作為坐標原點時還可選取甲車開始運動時刻作為計時起點，雖可采用分段函數討論求解，但求解過程繁瑣，未能體現統一坐標法的簡便性，對于其他的選取方式也是同樣不能體現本法的簡便性。

在長為200 m的斜面上，一滑輪愛好者以6 m/s的速度和30 cm/s的加速度從斜面底端滑上斜面，到達最高點折返后加速度大小不變；另一人在前者從底端出發時以7.2 km/h的速度和30 cm/s的加速度從斜面頂端滑下。求多長時間后兩人相遇以及相遇時兩人各自走過的路程。

建立以斜面底端為原點，沿斜面向上的Ox坐標，如圖3所示。以兩人開始運動時刻為計時起點。設滑上斜面的人為質點1，另一從斜面頂端滑下的人為質點2。其中a=a=-0.3 m/s，初始條件分別為 t=0 時，x=0，v=6 m/s；x=200 m，v=-2 m/s，則兩質點的運動學方程為

圖3 沿斜面建立Ox坐標系

對比常規解法：若采取常規方法求解，需要先討論在甲車開始運動的前t=6 s內兩車是否

設相遇時刻為 t＇，則

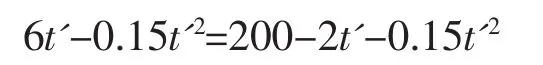
由此求得相遇時刻：t＇=25 s，即 25 s后兩人相遇。

（2）對（1）（2）兩式求時間導數，得到兩質點的速度方程

由此可見，質點1在t＇'=20 s時速度為零，到達最高點，隨后折返向下運動；將t＇'=20 s代入質點1的運動學方程可求得質點1運動的最高坐標為

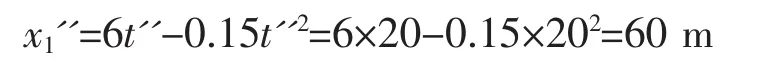
再將t＇=25 s，代入其中一個運動學方程（代入質點1的運動學方程），可求得兩人相遇時的坐標為

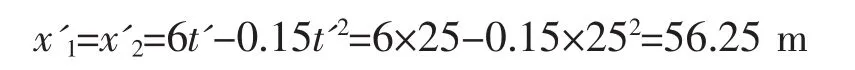
則兩人相遇時各自走過的路程分別為

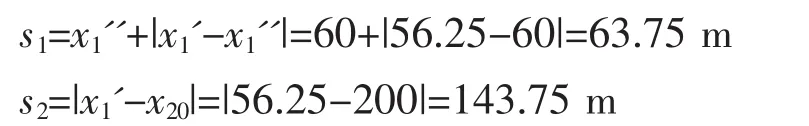
對比常規解法：該例題中兩質點的相遇可能是在質點1上升的過程中，也可能是在質點1折返后下降的過程中，若采用常規的方法求解需要分別討論質點1上升和下降的過程，運動過程復雜，列式繁瑣，稍有不慎極易出錯。采用統一坐標法，在同一時空坐標中描述兩質點的運動過程，對于兩質點的整個運動過程均適用，使該類問題迎刃而解。

①統一坐標法在求解追擊相遇問題的過程中，利用相遇條件x=x，得到關于時間的一元二次方程，通過方程是否有解判斷出兩質點是否相遇，如方程有解即可求出相遇時刻，若關于t時間的一元二次方程有兩個正解，則說明兩質點相遇兩次（例1）；若有一正解，則相遇一次（例2）；若無解，則不相遇。②部分讀者可能會誤認為“統一坐標法”就是前文提到的“數學函數法”，將兩者混為一談。兩者雖都是數理結合，表達形式相似，但卻有著本質的區別。統一坐標法利用時空坐標將時刻和空間位置進行了統一，把質點運動對應的位置坐標看作是時間的函數，從而對不同質點的運動進行描述；而“數學函數法”和以往的其他方法則是利用質點運動的時間間隔和空間位移關系描述質點的運動情況，僅描述單一質點的運動情況，對于多個質點的運動要分別進行討論。

4 總結

通過對使用統一坐標法求解直線運動的追擊相遇問題的歸納、概括，發現該法能夠便捷有效地解決此類問題，尤其是非單一運動過程、物理方程過多、計算量大的追擊相遇問題。從以上兩個頗具代表性的例題中可以看到，僅僅只需要列出質點的運動學方程、利用相遇條件即可求解直線運動的追擊相遇問題。但值得注意的是，位置坐標和計時起點的選取問題，兩者的選取遵循簡便計算的原則，根據具體條件靈活選取。與解決直線運動的追擊相遇問題的常規方法相比，“統一坐標法”具有一定的優勢，該法巧妙，簡便有效，是數理方法結合的典型代表。“統一坐標法”巧妙地利用了數學工具，將物理問題轉化為數學問題，實現了數學知識的遷移，優化了解題的程序，對啟發學生積極思考，多學科知識交叉融合，有積極的意義。