彈性碰撞與圓周率的奇妙聯系
葉志煒,黃樹清
福建師范大學物理與能源學院,福州 350117
中國古人計算圓周率是采取“割圓術”,南北朝時期的祖沖之在此基礎上將圓周率精確到小數點后的第七位,遠領先于同時期的國外圓周率的研究。而談到圓周率,我們往往想到的是數學中的求圓面積公式;談到碰撞,則往往想到的是物理中的彈性碰撞和非彈性碰撞。那么,彈性碰撞和圓周率有什么聯系呢?下面對此進行研究。
1 彈性碰撞分析
此問題并不復雜,我們首先從高中物理中一個常見的碰撞概念說起。兩個物體之間在極短時間內產生很大的相互作用力,然后速度發生了變化,這個過程就是碰撞。碰撞又可分為彈性碰撞(無機械能損失)、非彈性碰撞(部分機械能損失)和完全非彈性碰撞(機械能損失最大),本文所研究的是彈性碰撞范疇。
彈性碰撞中,最典型的一個碰撞模型如圖1所示。
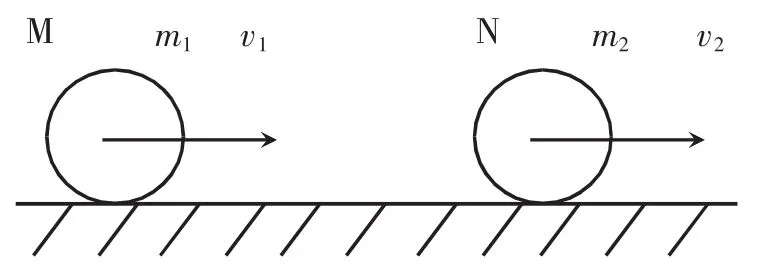
圖1 典型碰撞模型
在水平地面上有兩個小球,球M的質量為m,以速度v水平向右運動,另一個球N的質量為m,以速度 v也水平向右運動,且 v>v,兩速度在同一直線上,問兩球碰撞之后的運動狀態如何?
通常求解該問題時,我們都要利用動量守恒定律和機械能守恒定律得到兩個等式,然后再利用代數的方法進行求解,其中這兩個等式為

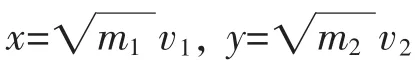
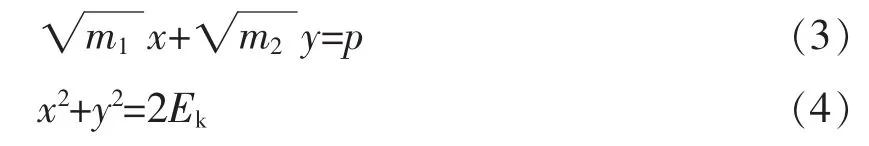
通過變換,我們成功地將方程簡化,由此便很容易將動量和能量所對應的圖像聯立畫出,如圖2所示。
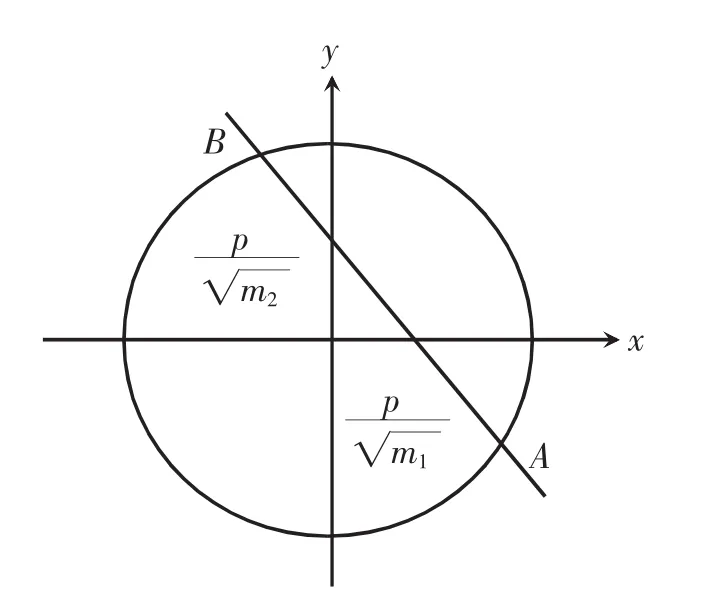
圖2 動量和能量對應的圖像
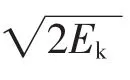
以上推論說明,通過數學中幾何的方法可以有效解決物體的碰撞問題。
2 圓周率與碰撞的聯系
那么,圓周率是怎么跟碰撞產生聯系的呢?假設有彈性非常好且光滑的豎直固定墻和水平地面,地面上左邊放著物體M,其質量為m(質量小);右邊放著物體N,其質量為m(質量大)。如圖3所示,初始物體N以初速度v向左運動與物體M發生碰撞,隨后物體M將會向左撞向墻面并反彈再撞物體N,如此反復碰撞直至停止,如果我們去統計物體M的碰撞次數,會發現碰撞的次數和圓周率的大小有著緊密聯系。分析可知,由于該過程還是彈性碰撞,所以依舊可以采用上文求得的幾何關系來進行深入分析。
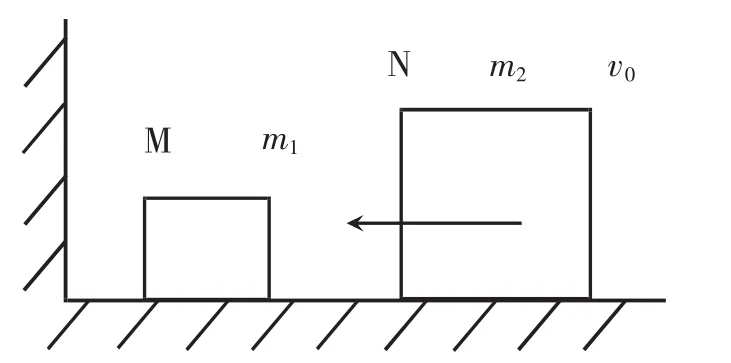
圖3 位于光滑地面上的M、N兩物體和豎直墻面之間的碰撞
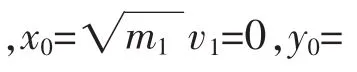
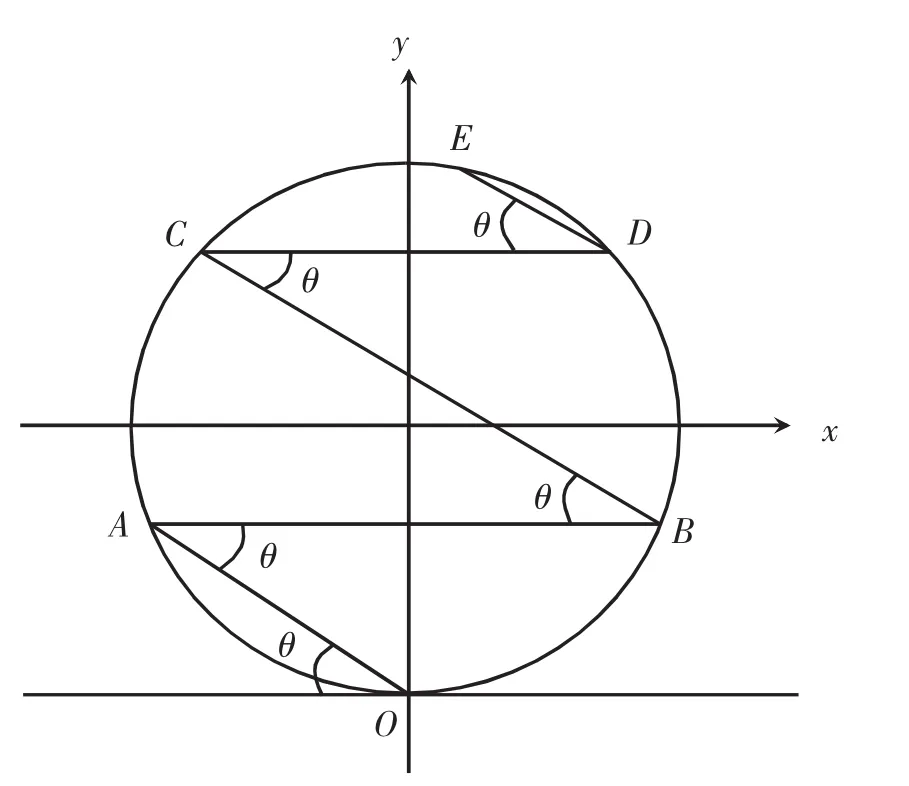
圖4 多次碰撞過程中x和y值的變化情況示意圖
繼續根據圖像可以分析得到,每碰撞一次對應著一段圓弧,而這段圓弧所對應的圓周角是θ,則可以得到碰撞N次之后,總的角度之和會比圓的圓周角小,即比圓周率的值略小,而碰撞N+1次后,會與圓周率的值相等或略大于圓周率,即

進一步化簡可得

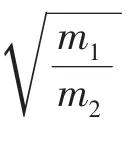
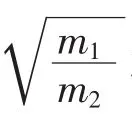
表1 與碰撞次數的關系
3 總結
本文通過非常規的數學幾何圖像的方式,推導得到圓周率與物體彈性碰撞之間奇妙的定量關系,揭示了數學與物理之間的奇妙聯系,同時也說明了具備良好的數學素養則可以更好地體會物理之美。

