三角形的秩和廣義三角函數

周仲旺 孫建安 （濰坊學院數學與信息科學學院，山東 濰坊 261061）

一、廣義勾股定理和三角形的秩

廣義勾股定理1對正實數a，b，c，若滿足a≤b＜c，則必存在唯一的正實數n，使a+b＝c，且當n＜1 時，a，b，c不構成三角形；當n＝1 時，a，b，c 構成平角三角形，當1＜n＜2 時，a，b，c 構成鈍角三角形；當n ＝2 時，a，b，c 構成直角三角形；當n＞2 時，a，b，c 構成銳角三角形.這個定理中的n 就稱為三角形的秩.

以橢圓的一個焦點為極點建立極坐標系，則橢圓的極坐標方程為ρ+c＝（a-ρ）、ρ+（a-ρ）＝c，其中a 是長軸，c 是焦距，ρ 是橢圓上一點的極坐標的極徑，n 是橢圓上這點和橢圓的兩個焦點構成的三角形的秩.

橢圓的頂點和兩個焦點構成的三角形是平角三角形或等腰三角形，這些三角形很特殊，四個頂點就很特殊，它們所在的位置就很好.據此，當橢圓（指第二個方程）上有點和兩個焦點構成的三角形為直角三角形時，就得到橢圓上這樣的四個點，這四個點很特殊，位置也很好，在橢圓的這四個位置上擺放東西肯定很好看、很美觀.譬如一個舞臺的邊緣是個橢圓，則主持人站在這些位置報幕最好.

二、三角形秩的理論意義

所以f（r，a，b）在a＞0，b＞0 上，當1＜r＜2 時，必有最小值f（r），最大值的上確界為0；當r＞2 時，必有最大值f（r），最小值的下確界為0，且若r＜r，則f（r）＜f（r），f（r）＜f（r）.

像直角三角形那樣，對任意實數r＞1 和任意銳角α，必有一個三角形，它的秩為r，一個較小角為α，且另外兩個角唯一確定，這一結論的前半部分，由三角形秩的理論意義能推出.據此，引入廣義三角函數.

三、廣義三角函數理論

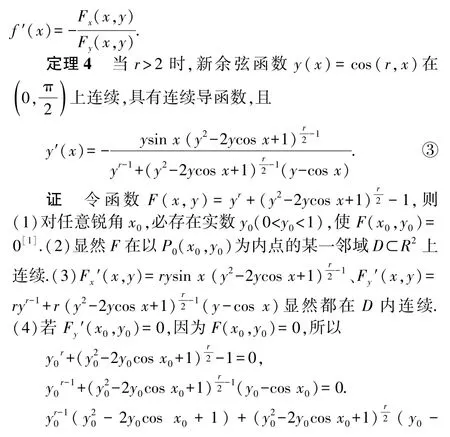
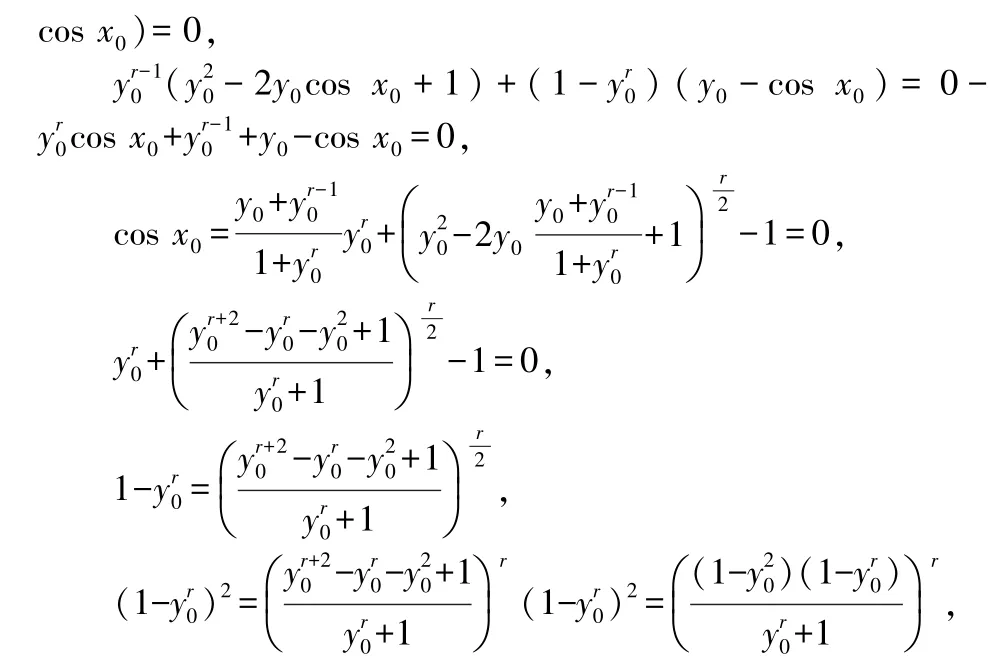
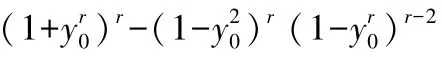
注：此定理不難推廣到區間（-∞，+∞）上，由①②③式，不難得到.

當x 是銳角且r＞2 時，

所以，當r＞2 時，cos（r，x），sin（r，x）的單調性很清楚了.sin′（r，x）是cos（r，x）乘一個因子，cos′（r，x）是-sin（r，x）乘這個因子，當r ＝2 時，這個因子是1，即得sin′x ＝cos x，cos′x＝-sin x.至此，r＞2 時的廣義三角函數cos（r，x），sin（r，x）已基本搞清楚，接下來請大家研究1＜r＜2 時的廣義三角函數.

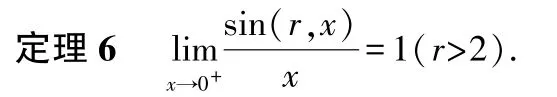
證由①②③式不難得：

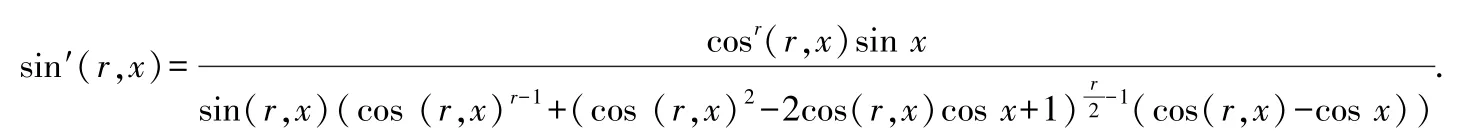
根據洛必達法則知：

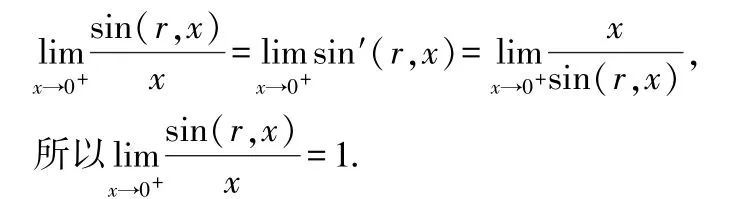
值得一提的是：根據②式，在原來基本初等函數的意義下，新余弦函數、新正弦函數基本沒有顯示式，但反新余弦函數、反新正弦函數都有顯示式.

經過簡單計算得：sin（3，0.3）＝0.297，sin（3，0.75）＝0.69，sin（3，1.25）＝0.96，sin（3，1.5）＝0.999，cos（3，0.3）＝0.99，cos（3，0.75）＝0.87，cos（3，1.25）＝0.48，cos（3，1.5）＝0.111.再根據單調性，不難作出sin（3，x）、cos（3，x）的圖像，它們與sin x、cos x 的圖像差不多.

上面我們研究了當r＝3，1.5 時，sin（r，x）、cos（r，x）的圖像，請大家自行研究r 取其他值時，sin（r，x）、cos（r，x）的圖像.

所有的新正弦函數、新余弦函數都應看成基本初等函數，sin x、cos x 其實就是sin（2，x）、cos（2，x），將sin x、cos x 寫為sin（2，x）、cos（2，x）更科學.cos（r，x）和cos x 之間滿足②式的關系，所以新增加的基本初等函數實際上只有兩個，即對一個固定的r 只有sin（r，x）和cos（r，x）.根據②式，cos（r，x）一般不能由cos x 表示，但cos x 都可由cos（r，x）表示.所以，凡是能用正弦、余弦表示的函數，必能用新正弦、新余弦表示，但是能用新余弦、新正弦表示的函數，一般不能用余弦、正弦表示，這說明廣義三角函數是比三角函數更基本的函數.三角函數跟廣義三角函數的圖像有時差不多，有時差別很大，所以，凡是能用三角函數研究的實際問題都能用廣義三角函數研究，不能用三角函數研究的實際問題也能用廣義三角函數研究.因此，只要把三角函數中隱含的秩2 改成廣義三角函數中的秩r 即可，這樣修改后，解決實際問題能否更精確、更便捷需要實踐的檢驗，遺憾的是這不是我們數學工作者所研究的問題.

四、解三角形的快捷方法

文獻［1］中引入了三角形的秩r＞1 和三角形的較小銳角α 的新余弦x ＝cos（r，α），給出了建立電子數學用表查cos（r，α）＝x、cos（x，r）＝α、cos（x，α）＝r 的方法，現對新正弦y ＝sin（r，α）作同樣處理，即也建電子數學用表查sin（r，α）＝y、sin（y，r）＝α、sin（y，α）＝r，并再增加三個新電子數學用表：①r（α，β）＝r，即已知三角形的兩較小銳角α，β可以查出它的秩r，這個表根據公式sinα+sinβ ＝sin（α+β）提出；②r（r，α）＝β，即已知三角形的秩r 和一個較小銳角α 可以查出它的另一較小銳角β，這個表也根據公式sinα+sinβ＝sin（α+β）提出；③r（x，y）＝r，即已知三角形的較小銳角α 的新余弦、新正弦x，y 可以查出它的秩r，這個表根據公式x+y＝1 提出.用與三角形的秩有關的上面這九個新函數取代電子計算器上的八個三角函數，則解三角形基本上查查計算器上的電子數學用表就行！由此可知，建坐標系不一定必須建直角坐標系，采用仿射坐標系和極坐標系也有其優點.以下說“查表得”實際上是用matlab 算出的，因為上面講的電子數學用表到目前為止還沒建起來.

建立如圖所示的仿射坐標系xOy，兩坐標軸的夾角為35°，A，B，C，D 四點的坐標分別為A（4，1），B（2，1.5），C（-1，y），D（-3，y），直線CD 的傾斜角是20°，試求：A，B兩點間的距離和C，D 兩點間的距離.

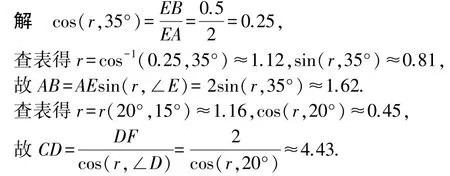
注1：在實際問題中，測量出的一般是角的度數，采用此法有明顯的優勢.

注2：三角形的秩是三角形的一個非常重要的參數，這一重要參數應寫進教材.

五、三角形的最大角的度數和它的秩數之間的對應關系表及其應用

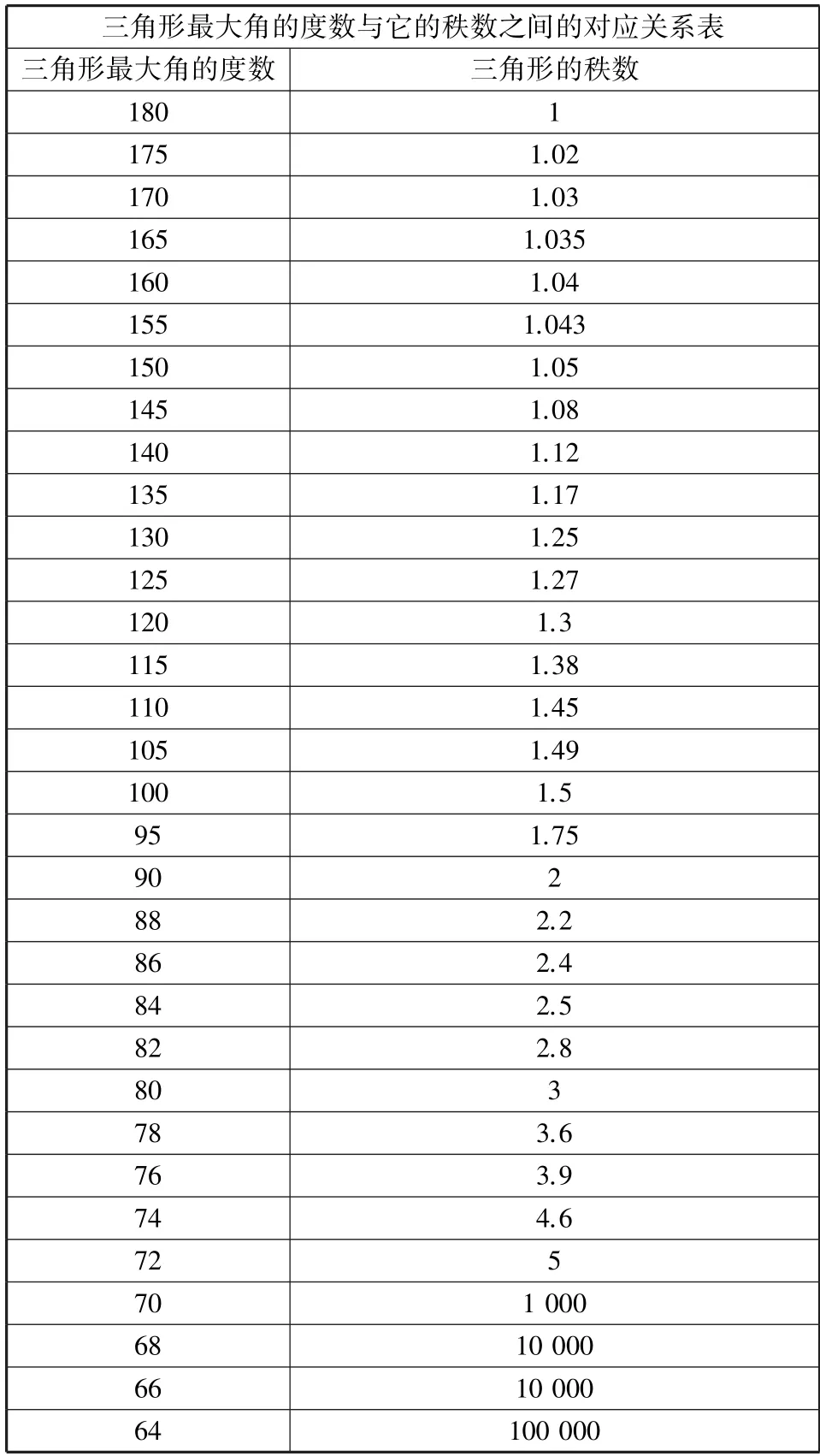
根據上面的表格，已知斜三角形的最大角和一邊就能解三角形.給出了三角形的最大角，在上面表格中查出它的秩，再結合第四部分給出的方法就可以解三角形了，這樣解三角形所得結果與其精確值基本一樣.這種解斜三角形的方法比解直角三角形的經典方法需要的條件要少，因此采用仿射坐標系就比采用直角坐標系要好，特別是仿射坐標系兩坐標軸的夾角較小（大）時.