基于ABAQUS 的多尺度有限元模型橋梁檢測與評估

■王晨輝

（福建博海工程技術有限公司，福州 350000）

有限元計算分析是橋梁檢測中的重要環節，MIDAS、 橋梁博士等專業軟件均采用梁單元進行力學分析。 梁單元模型無法準確計算實體的真實應力、應變和變形情況，不能細致分析局部載荷細節，使計算結果和真實情況存在偏差。 隨著科技的進步和軟件功能及性能的提升，ABAQUS 作為一款通用型有限元分析軟件，可以定義任意材料的屬性及模擬任意形狀的結構，不僅可對橋梁結構進行簡單的線彈性分析，還可進行復雜的幾何非線性和材料非線性模擬，并且可以對橋梁結構進行精細計算，在模型關注的重點區域完成局部受力分析[1-4]。

但是，ABAQUS 軟件計算結果的準確性，很大程度上是由有限元模型的類型來決定的：宏觀有限元模型網格大、計算時間短，但計算結果不準確；精細化有限元模型網格小，計算時間長，但計算結果準確[5-6]。 因此，平衡計算成本及計算精準的對立關系，是橋梁檢測力學分析的研究重點。

基于此，以ABAQUS 軟件為依托，將橋梁檢測中重點區域進行精細化建模并準確、合理地連接到整體模型中，以此建立可以細致分析重點區域受力情況的多尺度有限元模型。 通過矩形截面簡支梁計算驗證精細化有限元模型和宏觀有限元模型之間連接形式的正確性， 并以福建某實際橋梁工程為例，對比計算結果及檢測數據，進一步驗證多尺度有限元模型的準確性。

1 多尺度有限元模型方法

多尺度有限元模型包含了宏觀及精細化有限元模型，其單元節點的自由度和精度不同，因此保證不同單元界面之間正確合理地連接是多尺度有限元模型建立的重難點[7]。 當宏觀有限元模型和精細化有限元模型分別建立時，主要考慮邊界條件的轉換問題，二者的連接可采用多邊界插值法、雙重子模型法、子模型法等方法；當宏觀有限元模型和精細化有限元模型混合建立時，是不同維度單元的連接問題，二者之間的連接通常采用多點約束法[8-9]。

多點約束法是將一種節點自由度的耦合關系建立的多點約束方程，能處理線性及非線性的約束問題，包含梁類型約束、線性約束、鉸結約束、綁定約束等。 對于復雜的約束可以通過設置自由度矩陣來實現連接關系[10]。 多點約束法的基本表達式如公式（1）。

其中uB和up分別為單元界面連接處的節點位移向量，C 為界面連接約束方程的系數矩陣。

通過圖1 可以直觀了解線性約束的原理，c 點被a、b 兩點通過自由度線性插值的方式約束著。 將宏觀有限元模型與局部精細化有限元模型建立在同一個模型中，通過多點約束法進行連接過渡的多尺度有限元模型被認為是計算精度最好且計算成本最少的方法。

圖1 多點約束線性耦合方式

2 矩形截面簡支梁的算例驗證

為了全面比較梁單元模型與多尺度有限元模型的計算優劣，以及驗證多點約束法在多尺度有限元模型計算中的有效性以及正確性，建立1 個矩形截面簡支梁， 分別采用MIDAS 軟件和ABAQUS 軟件進行分析計算。 矩形截面梁B×H=300 mm×400 mm，總長度L=6 000 mm，材料彈性模量1.93×105 MPa，泊松比0.3，容重79 kN/m3。荷載為結構自重及跨中區域500 kN 集中力。 采用MIDAS 軟件對簡支梁進行建模分析，模型見圖2，網格劃分見表1，計算結果見表2。

圖2 矩形截面簡支梁MIDAS 計算模型

依據《公路橋梁荷載試驗規程》，簡支梁重點關注區域為最大正彎矩的跨中截面，因此將跨中區域建立為精細化有限元模型，其長度取L/5 進行建模，跨中作用集中力大小為F=500 kN， 共建立3 種不同精度的有限元模型，對跨中截面應力及變形進行對比分析，模型見圖3，網格劃分見表1，計算結果見表2。

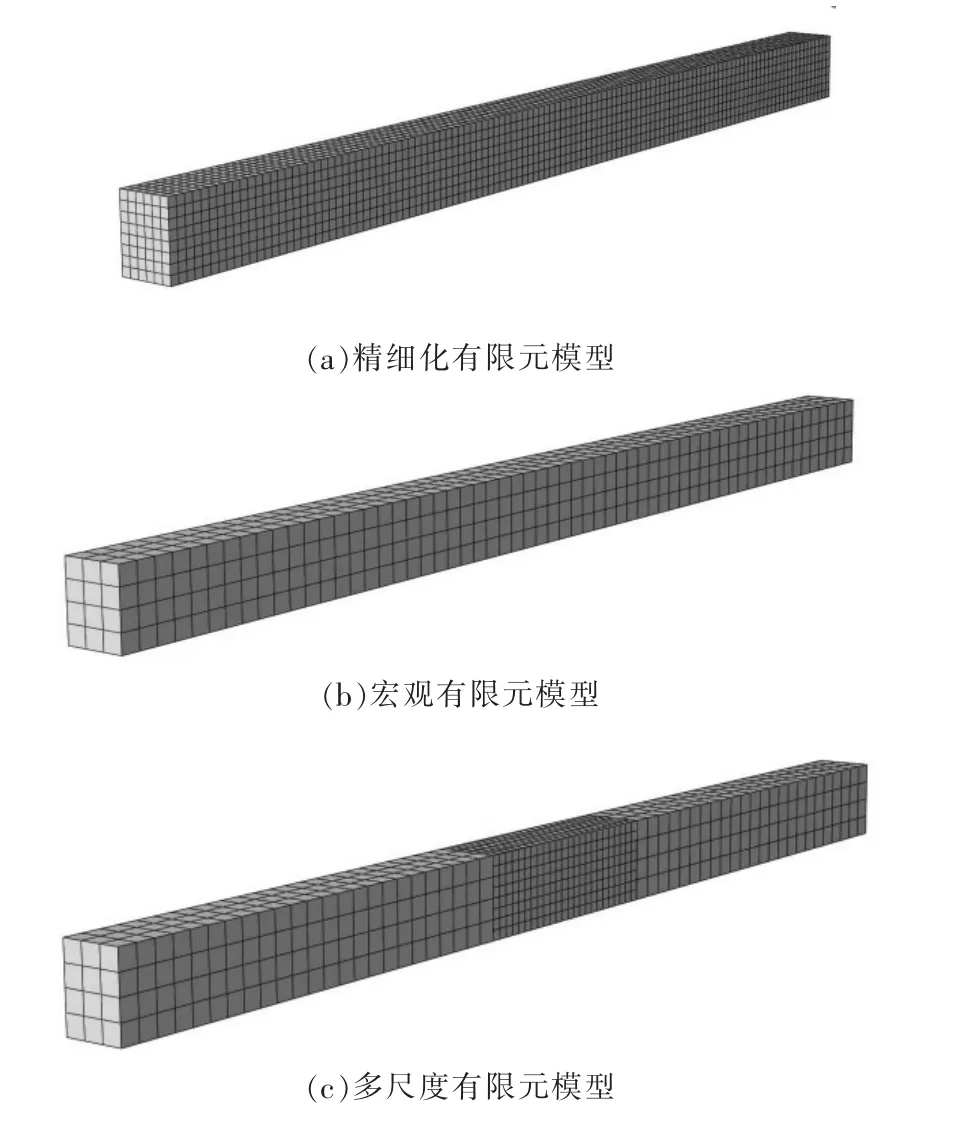
圖3 矩形截面簡支梁ABAQUS 計算模型

表1 矩形截面簡支梁不同類型有限元模型網格劃分

表2 矩形截面簡支梁不同類型有限元模型計算結果

由表1 和表2 可知， 當MIDAS 軟件的梁單元有限元模型與ABAQUS 軟件的精細化有限元模型采用相同大小的網格進行計算時，MIDAS 模型計算比ABAQUS 精細化模型計算的撓度值大6%，應力值大2%。由表2 可知，宏觀有限元模型與精細化有限元模型目標解計算的撓度值偏差6%、 應力值偏差18%；而多尺度有限元模型與精細化有限元模型目標解計算的撓度值偏差3%、應力值相同。 同時，多尺度有限元模型計算時長比精細化有限元模型目標解計算時長減少85%。 由此可得，采用MIDAS軟件梁單元模型進行有限元分析時，計算結果偏差較大；多點約束法在多尺度有限元模型的力學計算中是可行的、正確的，既滿足了計算結果的準確性又大大減少了計算成本。

3 工程實例分析

3.1 工程簡介

為了驗證多尺度有限元模型在橋梁檢測中的適用性，以福建某實際工程大橋為例進行驗證分析。 該大橋左幅起點樁號K0+091.014， 終點樁號K0+697.514， 橋梁長606.5 m， 橋跨布置為5×（4×30）m 預應力現澆箱梁。右幅起點樁號K0+211.014，終點樁號K0+697.514，橋梁長486.5 m，橋跨布置為4×（4×30）m 預應力現澆箱梁。 橋梁按雙幅設計，兩幅之間設5 m 中分帶，單幅橫斷面布置圖見圖4，具體截面尺寸及實景見圖5～6。

圖4 福建某實際工程大橋單幅橫斷面布置圖

圖5 福建某實際工程大橋單幅橫斷面結構尺寸圖

圖6 福建某實際工程大橋實景圖

3.2 構建多尺度有限元模型

使用ABAQUS 軟件對該橋進行計算分析，依據CJJ/T233-2015 《城市橋梁檢測與評定技術規范》以及該橋的對稱性、 重復性特點， 取左幅第二聯的120 m 連續梁進行有限元分析， 測試重點關注區域為墩頂截面及每跨的跨中截面，因此在建立多尺度模型時將墩頂1.4 m 及每跨6 m 跨中位置建立精細化有限元模型，其余位置按宏觀有限元模型進行建立。 精細化有限元模型和宏觀有限元模型用多點約束法進行連接，保證節點過渡的協調，建立的多尺度有限元模型見圖7。

圖7 多尺度有限元模型

3.3 測點布置及加載方案

本次橋梁靜力荷載試驗的加載工況，分為3 級逐級加載到最大荷載，然后一次性卸零。 采用水準儀測量測試跨跨中截面的撓度值，采用應變計測量測試跨跨中截面和支座截面的應變值。 測點布置見圖8～10，加載位置見圖11。

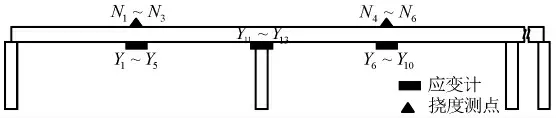
圖8 左幅橋應變/撓度測點立面布置圖

圖9 左幅橋跨中截面應變/撓度測點橫向布置圖

圖10 左幅橋墩頂截面應變測點橫向布置圖

圖11 車輛加載平面圖

3.4 靜載結果分析

將分級加載的結果進行匯總，采用多尺度有限元模型計算的結果與實測值進行對比，同時由CJJ/T233-2015《城市橋梁檢測與評定技術規范》中規定校驗系數η 為實測應變（撓度）與理論計算應變（撓度）之比。 應變結果匯總見表3～4，撓度結果匯總見表5。

表3 荷載作用下跨中截面應變結果匯總 （單位：με）

表4 荷載作用下墩頂截面應變結果匯總 （單位:με）

表5 荷載作用下跨中截面撓度結果匯總 （單位：mm）

由表3～5 可知，校驗系數大小比較均勻，校驗系數位于0.5～0.9，小于CJJ/T 233-2015《城市橋梁檢測與評定技術規范》中的規定限值1，所以該大橋剛度滿足試驗荷載要求。

3.5 模態分析

福建某實際橋梁工程多尺度有限元模型計算的理論基頻和實測基頻分別為4.07、4.79 Hz， 可知多尺度有限元模型計算的橋梁基頻和實測基頻基本一致， 再次說明了多尺度有限元模型的正確性。實測的自振頻率大于有限元軟件的計算值，說明該橋梁的性能滿足要求。

4 結語

橋梁結構關鍵部位應力及變形是橋梁檢測重點關注的指標，為了獲得更加準確的計算精度，精細化網格劃分造成的計算成本也成倍增加。 為了平衡二者的對立關系，以ABAQUS 軟件為依托，將橋梁檢測中重點區域進行精細化建模并準確、合理地連接到整體模型中，以此建立可以細致分析重點區域受力情況地多尺度有限元模型，并分別通過矩形截面簡支梁及福建某實際橋梁工程為例，來驗證本研究提出的多尺度有限元模型的準確性，研究結果表明：（1）采用多點約束法可準確實現不同網格大小的有限元模型之間的連接， 形成多尺度有限元模型；（2）多尺度有限元模型網格單元數、節點數均比精細化有限元模型少，使計算時長大大減少；（3）多尺度有限元模型撓度值、應力值、應變值等計算與精細化有限元模型得到的計算結果誤差在3%。 因此，對于大橋及特大橋橋梁檢測進行理論計算分析時， 可采用本研究提出的多尺度模型進行計算分析，既可提高計算精度，也可平衡計算時間成本。