波流相互作用下潮流能無軸輪緣導管渦輪機水動力特性與尾流結構分析

宋 科， 楊邦成

（1.昆明學院 機電工程學院， 云南 昆明 650214； 2.昆明理工大學 建筑工程學院， 云南 昆明 650500）

0 引言

近年來， 隨著各國對環境問題的愈加關注以及對碳排放實施更為嚴格的管控， 促使能源結構加快向綠色低碳型轉型， 特別是向高比例的清潔可再生能源轉型。 能源結構的轉型不僅可以改善環境質量、應對氣候變化，還可以培育新的經濟增長點，實現經濟社會可持續發展。作為一種可再生能源， 潮流能具有豐富的儲備資源和較高的可預測性，在過去十年中，利用潮流能進行發電的相關技術得到了長足的進步與發展[1]。 目前，潮流能發電技術主要分為渦輪系統和非渦輪系統（振蕩水翼、振蕩轉子等技術）兩種。其中，渦輪系統在性能和可靠性方面具有較好的水平[2]，目前，全球部署了許多兩葉或三葉的水平軸渦輪機系統[3]。 此外，為了提升潮流能渦輪機的行業競爭力與吸引力，有學者提出了帶導管的渦輪機系統以提高其能量獲取效率。 王樹杰[4]研究了導管形狀對渦輪機的水動力學性能的影響， 發現導管參數對渦輪機的能量獲取性能有很大的影響。 Belloniet S K[5]使用RANS-BEMT 模型分析了導管渦輪機的水動力學性能。 宋科[6]從多個方面對一種薄壁導管渦輪機的水動力學性能進行了分析。 劉清照[7]研究了導管安裝角度對渦輪機水動力性能的影響。 Tampier G[8]對導管渦輪機的水動力損失因子進行了計算和研究。 程帥兵[9]研究了導管間距對渦輪機水動力性能的影響。

現階段， 導管渦輪機技術已經具備一定的商業化運作氛圍， 并在一些沿海國家實現了并網發電。盡管該技術為行業領域開辟了新的方向，實現了潮流能的高效利用，但同時也存在一些問題，如導管渦輪機需要一定的軸系支撐結構來保證葉輪、電機與外部導管的匹配定位，而軸系支撐結構的存在必然會造成一定的流動干擾與阻力， 從而影響導管渦輪機系統的運行穩定性。 為了解決該問題， 筆者提出一種新概念導管渦輪機系統-無軸輪緣導管渦輪機。 這種導管渦輪機系統去除了傳統的軸系支撐結構， 將發電機系統內置安裝在導管的殼體內部， 以徑向安裝代替了傳統軸向安裝，并采用“發電系統-輪緣葉輪-導管”的一體化設計，使系統結構更加緊湊，通過輪緣葉輪與導管內側的徑向匹配，去除了輪轂結構，當系統運行時通過輪緣葉輪的旋轉帶動內置的發電機系統同步旋轉。 因此，相比傳統的導管渦輪機，無軸輪緣導管渦輪機不需要安裝軸系支撐結構， 在實際運行時可大大減小流動阻力和干擾， 提升了系統的穩定性和可靠性[10]。

在實際的潮流環境中， 無軸輪緣導管渦輪機不可避免的要在波浪、剪切流、偏流等混合工況下運行， 而對其在上述工況下的水動力特性進行評估至關重要。為此，本文以齋堂島海域的潮流條件為背景，對一無軸輪緣導管渦輪機進行了分析，探討了其在順流和偏流條件下的水動力特性及尾流結構形態， 以期能更好地了解無軸輪緣導管渦輪機在實際潮流條件下的運行狀態， 并為其合理布置提供一定的參考依據。

1 模型與計算方法

1.1 控制方程

假定流體不可壓縮， 控制方程分為連續方程及動量方程，雷諾時均的Navier-Stokes 方程可表示為

1.2 水動力學參數

渦輪機的水動力性能可用葉尖速比（TSR）、功率系數（CP）和推力系數（CT）表征，其計算式分別為

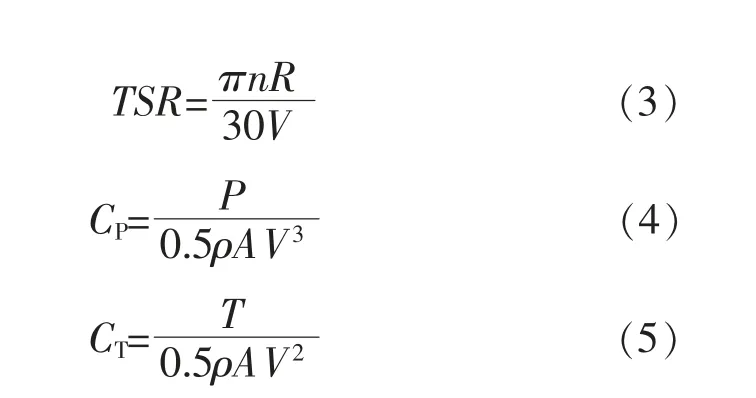
式中：n 為渦輪機轉速，r/min；R 為葉輪半徑，m；P為渦輪機的輸出功率，W；T 為葉輪軸向推力，N；A為葉輪旋轉掃掠面積，m2；V 為來流流速，m/s。

1.3 計算模型與網格劃分

本文的無軸輪緣導管渦輪機由輪緣葉輪與導管組成，其中葉輪為“三葉”水平軸葉輪，其直徑D為2 m，轂徑比為0.1；導管為“類翼型”環形截面后置導管。在葉輪的基礎上稍作調整，取消輪轂部分，并用輪緣連接葉尖，輪緣寬度比葉尖的軸向跨度略大。 將調整后的輪緣葉輪與導管內壁的喉部位置進行裝配得到無軸輪緣導管渦輪機。 設置計算域中渦輪機的中心距入口距離為5D，渦輪機中心至出口距離為15D， 模型阻塞度小于1.0%，入口設置為速度入口，出口設置為壓力出口，輪緣葉輪及導管為固壁面無滑移壁面條件。 將計算域劃分為旋轉域和靜止域。 無軸輪緣導管渦輪機模型與計算域的示意圖如圖1 所示。

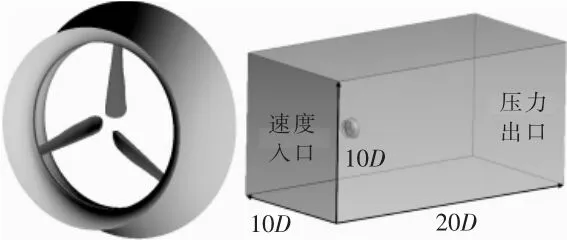
圖1 模型及計算域Fig.1 Model and calculation domain

假設來流速度為1.56 m/s， 參考長度為葉輪直徑（2 m），則系統的雷諾數約為3.1×106。 設置葉輪第一層邊界層網格滿足y+=1， 導管第一層邊界層網格滿足y+=10。 采用SST k-ω 湍流模型和滑移網格模型模擬非定常旋轉效應， 動靜交界面采用interface 設置，設置葉輪每旋轉1.8°作為一個時間步長，每步的計算殘差收斂最小值小于10-3,總計算時長為30 s，并取計算穩定的后6 s 作為分析結果。 此外，對無軸輪緣導管渦輪機在V=1.56 m/s 和TSR=4 的條件下進行網格數無關驗證，結果如表1 所示。由表1 可知，當網格數超過600 萬后，CP和CT基本不變。 對距導管渦輪機軸線距離為2D 的附近體網格進行加密， 最終網格劃分總數為800 萬左右，其中旋轉域約為190 萬，靜止域約為610 萬，網格細節如圖2 所示。

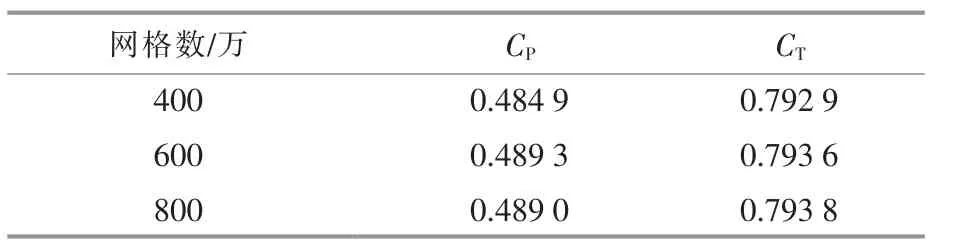
表1 網格數無關驗證Table 1 Mesh independence assessment results

圖2 網格細節Fig.2 Mesh details

1.4 數值驗證

為了確保數值模擬的準確性， 本文對葉輪在5 種來流速度下的CFD 結果與實驗值[11]進行了比較，結果如圖3 所示。 從圖3 可以看出，兩者吻合度較好，驗證了本文數值模型及方法的可靠性。

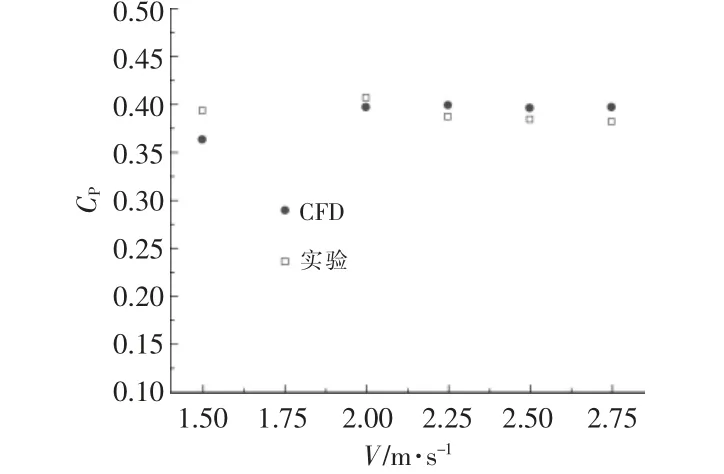
圖3 實驗數據與CFD 結果的對比Fig.3 Comparison between experiment and CFD

1.5 波流條件設置

以齋堂島海域的實際潮流條件作為研究背景， 該海域的日常極限波浪參數為波高0.6 m，波長24.8 m，頻率3.2 s，水深（H）與流速的關系[12]如圖4 所示。由圖4 可知，當水深為0～10 m（5D）時，流速約為1.56 m/s，且流速與水深的斜率，即流速剪切率為0.002。 依照該潮流條件，將速度入口條件設置為（1.56±0.002）H m/s，無軸輪緣導管渦輪機的中心距水面的距離為1D。

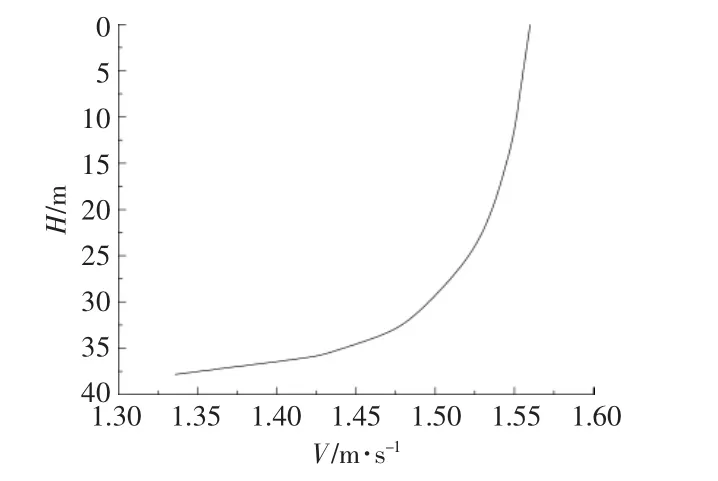
圖4 水深與流速的關系Fig.4 The relationship between water depth and velocity

2 結果與分析

2.1 順流條件

在不同TSR 下， 無軸輪緣導管渦輪機的CP和CT隨時間的變化曲線如圖5 所示。由圖5 可以看出：當TSR=4 時，渦輪機處于最佳TSR 范圍附近， 隨著TSR 的增大， 渦輪機的平均CP逐漸降低，而平均CT逐漸升高；CP和CT的波動幅度也隨TSR 產生一定的變化， 隨著TSR 的增大，CP和CT的波動幅度逐漸增大；當TSR=5 時，CP和CT的波動幅度分別比TSR=4 時增加了8.4%和17.3%；當TSR=6 時，CP和CT的波動幅度分別比TSR=4 時增加了31.9%和40.9%。 由于受到波流的影響，無軸輪緣導管渦輪機在一個波流周期內的CP和CT產生了明顯的周期性波動， 且波動頻率與波浪頻率保持一致。在波流的作用下，無軸輪緣導管渦輪機附近的流體速度分布發生了明顯的變化。 當波峰位于無軸輪緣導管渦輪機正上端時， 將誘導周圍水流迅速加快， 使渦輪機的CP與CT達到最大值；而當波谷位于無軸輪緣導管渦輪機正上端時，將誘導水流迅速減慢，使CP與CT處于最小值。

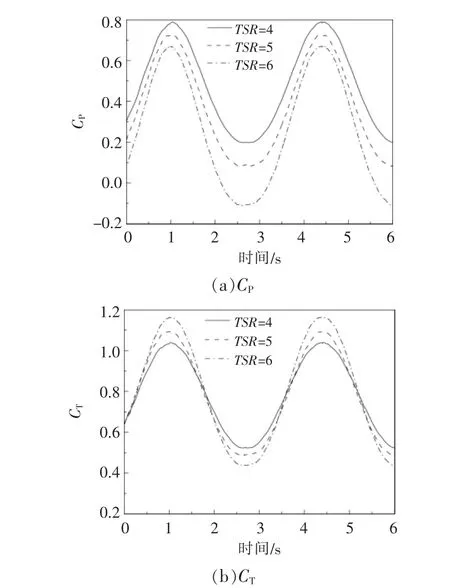
圖5 不同TSR 下的CP 和CT 隨時間的變化曲線Fig.5 CP and CT versus times curve under different TSR

當TSR 不同時，無軸輪緣導管渦輪機在波流條件下的渦量（上圖）與湍動能（下圖）分布如圖6所示。從圖6 可以看出，無軸輪緣導管渦輪機尾部存在導管后緣處的分離渦及葉輪軸心處獨特的軸心射流渦。 由于導管外側截面處出現了一定的流動分離， 導致一部分渦流能量從導管后緣邊界處脫落并向下游傳播。受波流的影響，該部分渦流在向下游傳播的過程中呈現出不規則的形態， 其強度與范圍也在不斷變化。 隨著TSR 的增大，尾旋渦流強度有所上升， 也導致其不規則程度有所增加。 此外， 由于無軸輪緣導管渦輪機沒有輪轂結構，軸心處存在一定面積的開放缺口。當無軸輪緣導管渦輪機運行時，葉輪前后將產生壓力差，該壓力差將迫使一部分來流通過該開放缺口泄流而出， 并形成軸心射流渦（此處的流速高于來流量級）。 隨著TSR 的增大，葉輪前后的壓力差有所減小，導致通過葉輪開放缺口處的流量下降。 因此，軸心處的渦流的范圍隨著TSR 的增大而減小，并隨著下游距離的延伸而逐漸消散至周圍流場中。

圖6 不同TSR 下的渦量與湍動能分布Fig.6 Vorticity and turbulent kinetic energy distribution under different TSR

2.2 偏流條件

當TSR=4 時，無軸輪緣導管渦輪機在不同偏流角下的CP和CT隨時間的變化曲線如圖7 所示。 從圖7 可以看出：當偏流角為40°時，無軸輪緣導管渦輪機的平均CP和CT分別比偏流角為20°時降低了18.9%和10.7%；當偏流角為60°時，無軸輪緣導管渦輪機的平均CP和CT分別比偏流角為20°時降低了70.0%和45.5%； 處于偏流條件下的無軸輪緣導管渦輪機CP和CT依然表現出與波流頻率一致的周期性波動。 但由于偏流增加了其運行的復雜性， 使葉輪前后端的壓力差處于高度不穩定的狀態， 導致CP和CT在一個波流周期內出現了額外的波動，且隨著偏流角的增大，該額外波動的振幅也逐漸增大。 當無軸輪緣導管渦輪機處于偏流條件下時，首先，葉輪的葉素截面的相對攻角分布將發生改變；其次，葉輪旋轉平面來流向的投影面積將會減小；最后，導管的入口流量也將減小，其聚流抽吸能力有所減弱。最終使無軸輪緣導管渦輪機的CP和CT逐漸由軸向分量轉移至側向分量，導致其平均CP和CT逐漸降低，且偏流角越大，平均CP和CT下降的越快。

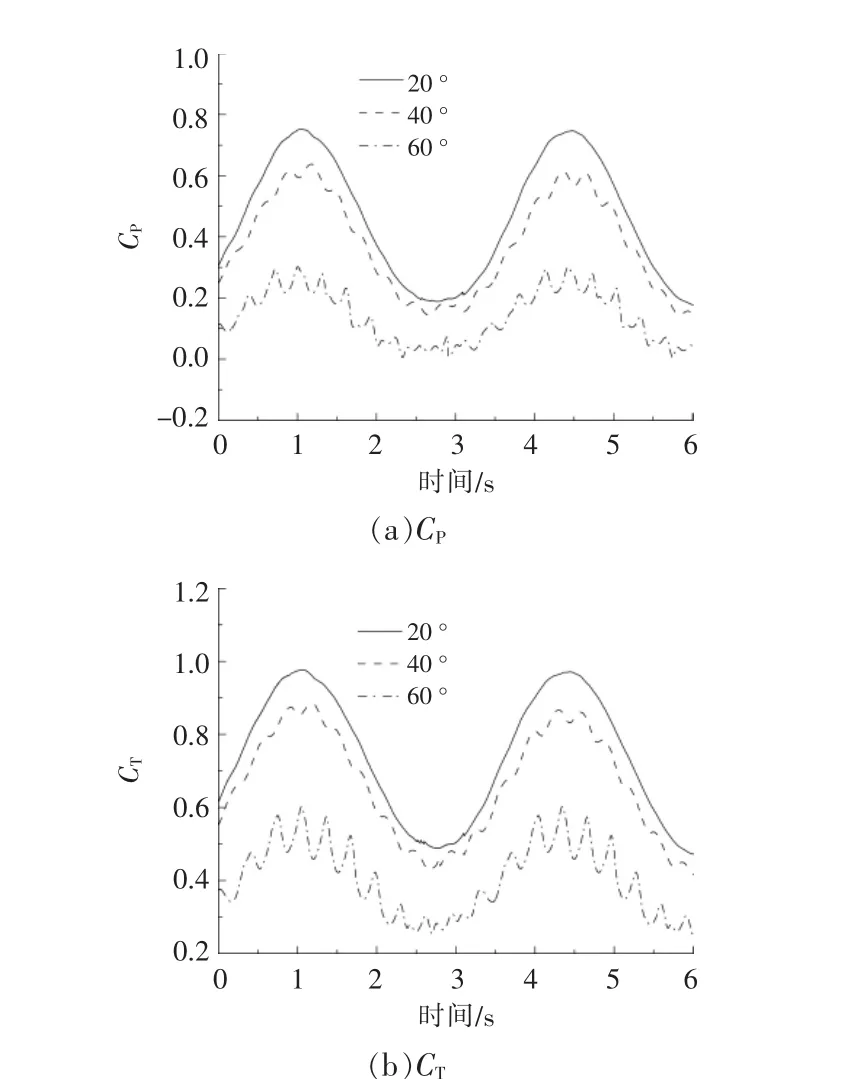
圖7 不同偏流角下CP 和CT 隨時間的變化曲線Fig.7 CP and CT versus times curve under different yaw angles

當偏流角不同時， 無軸輪緣導管渦輪機在波流條件下的渦量（上圖）與湍動能（下圖）分布如圖8 所示。從圖8 可以看出，偏流條件下的渦流能量分布不同于順流條件下的渦流能量分布（渦流能量分布都發生了側向的偏移和變形）。當來流與無軸輪緣導管渦輪機結構接觸時， 由于來流方向與渦輪機軸心不在一條直線上， 流體將按照流動阻力最小的路徑， 繞開導管偏轉的一側外壁面并誘導形成相當程度的流動分離低速區， 該低速區直接導致了大范圍的分離渦和高湍動能區， 而導管另一側的后緣內側也會脫落形成一定范圍的分離渦并向下游傳播。受波流的影響，該部分渦流能量的強度與范圍會不斷發生變化， 并在向下游傳播的過程中呈現出極其復雜的非對稱形態。 隨著偏流角增大，其復雜程度也逐漸增加。 此外，一部分來流依然可以通過軸心處的開放缺口泄流而出，但隨著偏流角的增大， 該開放缺口在來流向的投影面積逐漸減小，導致軸心射流渦范圍所有下降。

圖8 不同偏流角下的渦量與湍動能分布Fig.8 Vorticity and turbulent kinetic energy distribution under different yaw angles

2.3 討論

由上文的分析結果可知，在一定范圍內，波流相互作用下的無軸輪緣導管渦輪機將承受較大的水動力波動載荷的影響（尤其是當渦輪機轉速較高或者偶遇偏流工況時）。 此外，所有這些波動載荷也將傳遞到渦輪機內部的元件上， 這也間接地加速了這些內部元件的磨損和疲勞程度， 給整個系統的能量輸出穩定性和結構安全性都帶來了一定的挑戰。 鑒于潮流能發電系統的制造和維護成本都很高，且至少要保證在25 a 內無需大修或更換主要部件[13]。因此，可采用以下措施應對上述不利影響。

①盡量使渦輪機處于較低的TSR 范圍內運行 （渦輪機最佳的輸出功率匹配于低TSR 范圍內）。此外，為了減小偏流的影響，應加裝偏流旋轉自適應裝置， 使來流方向與無軸輪緣導管渦輪機軸向偏差在一個較小角度內。

②采用全復合材料葉片， 可在一定范圍內降低水動力性能的波動幅值；或者采用合金為主體，復合材料包裹的葉片制造工藝， 可在保證葉輪剛度的同時，起到一定的抗機械疲勞，阻止表面裂紋擴展的葉片延壽作用。

③增加無軸輪緣導管渦輪機遠程故障診斷與監測工序，提早鎖定損傷部件，在葉片等結構發生斷裂前進行修復。

3 結論

本文依據齋堂島海域的實際潮流條件對一種新型潮流能無軸輪緣導管渦輪機在波流相互作用下的水動力特性與尾流結構進行了三維非定常數值模擬研究，得出以下結論。

①在順流條件下，受波流效應的影響，當TSR不同時， 無軸輪緣導管渦輪機的CP和CT均產生了明顯的周期性波動， 波動頻率與波浪頻率保持一致，且隨著TSR 的增大，CP和CT的波動幅度逐漸增大。

②在偏流條件下， 無軸輪緣導管渦輪機的平均CP和CT均隨著偏流角的增大而降低， 而偏流也將導致CP和CT在一個波流周期內出現額外的波動， 且該額外波動的振幅隨偏流角的增大而增大。

③受波流效應的影響， 無軸輪緣導管渦輪機的尾流在向下游傳播的過程中呈現出復雜的形態，其強度與范圍也會不斷發生變化，且隨著TSR和偏流角的增大，其復雜程度也在逐漸增加。

④由于無軸輪緣導管渦輪機沒有輪轂結構，軸心處存在一定面積的開放缺口。在一定條件下，一部分來流將通過該開放缺口泄流而出并形成射流渦，而隨著TSR 和偏流角的增大，射流渦范圍將有所減小。