L2上復變函數的洛朗級數逼近

楊 剛

(云南大學數學與統計學院,云南昆明 6505000)

0 引言

精確的Jackson不等式研究已經有50余年的歷史,為了敘述已有的研究結果,先敘述一些相應的記號;L2(U)表示自變量在區域U內平方可積的復函數空間.在L2(U)上定義函數f范數為

這里|f(z)|表示函數f的模,Pn為次數不高于n的代數多項式函數空間.函數空間Pn對函數f的最佳逼近En-1(f)2[6]表達式為

En-1(f)2∶=inf{‖f-g‖2∶?g∈Pn-1}.

在復數域上K泛函[1]表達式為

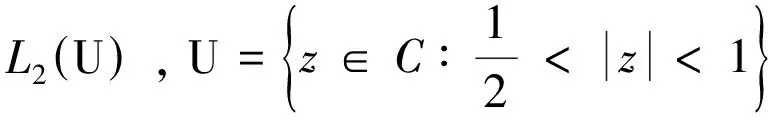
在實數域R上,參考文獻[8-13]得到關于m階連續模和K泛函的相關逼近定理,孫永生[14]介紹了精確Jackson不等式的具體形式.為研究一些函數類的最佳逼近提供了重要的不等式.

1 預備知識

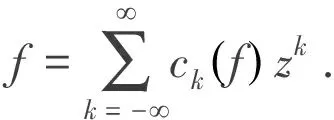
對函數f求r階導,則有

令bk,r=(-k)(-k-1)…(-k-r+1),ak,r=(k)(k-1)…(k-r+1),即

E(n-1,n-1)(f)2∶=inf{‖f-g‖2∶g∈P(n-1,n-1)}=‖f-S(n-1,n-1)‖2；

(1)

這里E(n-1,n-1)(f)2表示用函數g逼近f得到的最佳逼近.P(n-1,n-1)表示z-1和z的次數都小于等于n-1的函數空間.

2 關于K泛函的精確Jackson不等式和E泛函的不等式

下面給出函數f的最佳逼近E(n-1,n-1)(f)2與函數zrf(r)的最佳逼近E(n-1,n-1)(f)2的關系.

定理1>對于n∈N+;r∈Z+;n>r≥1，則

(2)

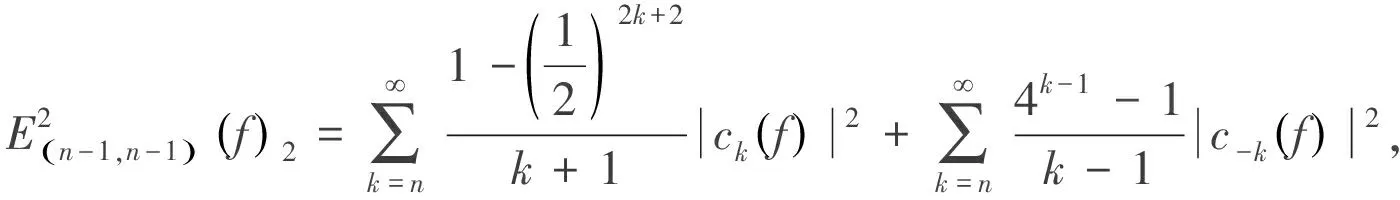
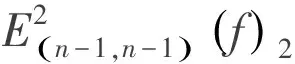
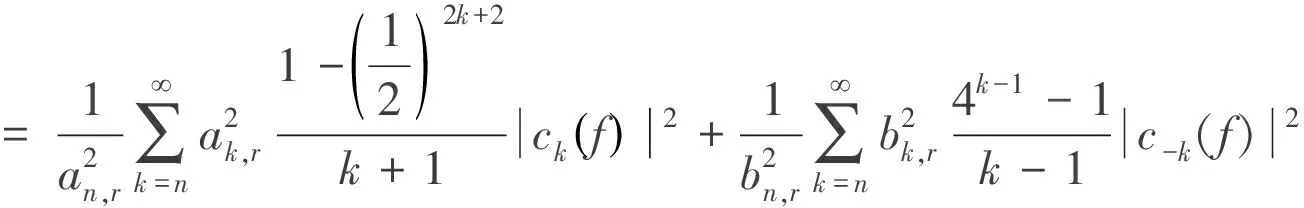
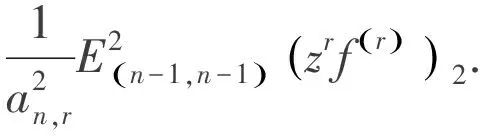
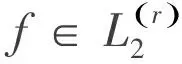
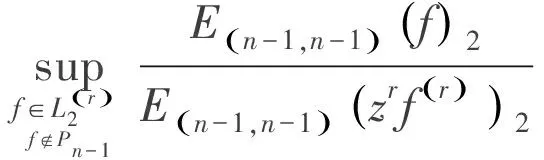
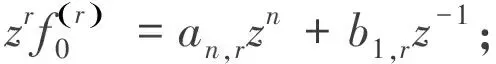
從而可以估計(2)式左邊的下界

證明.

推論1>對于n∈N+;n>1r=1，則

(3)

定義1[1]特殊K泛函的定義為

(4)

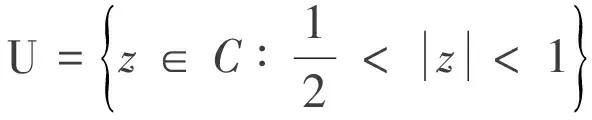
下面得到特殊K泛函與函數f的最佳逼近E(n-1,n-1)(f)2的精確Jackson不等式.

定理2 對于n∈N+;n>1;t∈(0,+∞)，則有

(5)

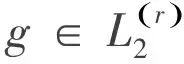
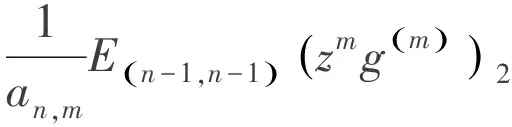
由公式(4)知

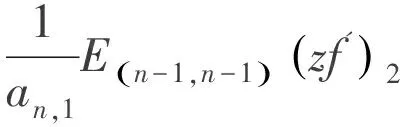
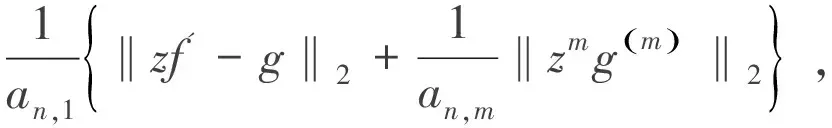
根據K的定義，從而得到(5)式右邊的上界

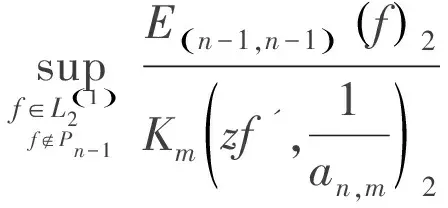
從而得到(5)式左邊的下界

證畢.

定義2[2]在L2空間上特殊的E泛函的定義

E(t,f;L2)∶=inf{‖f-f0‖L2;‖f0‖L2≤t},t∈(0,+∞)，

(6)

在L2空間上通常簡寫成E(t,f;L2)∶=inf{‖f-f0‖2;‖f0‖2≤t}.

定理3 對于n∈N+;n>1;t∈(0,+∞)，則

(7)

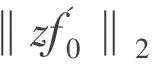
令

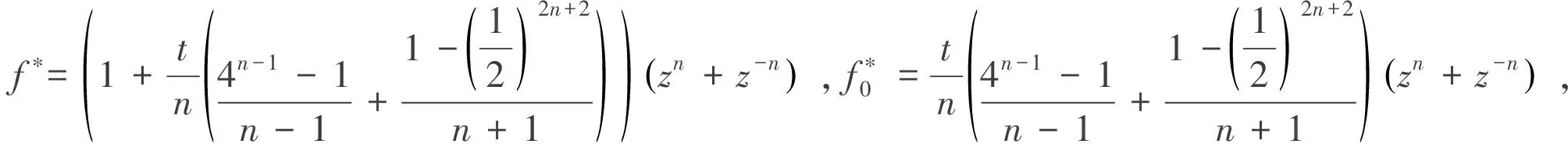
從而可以估計(7)式左邊的下界

證畢.

3 函數類的最佳逼近

介紹函數Φ(t)=M(1+t2),M是一個充分大的正數.下面介紹二種函數類的定義.

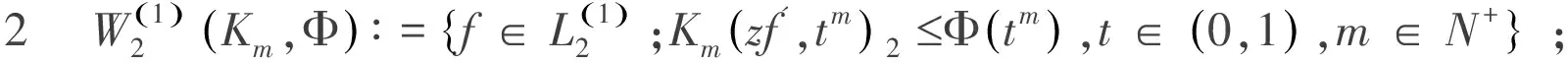
E(n-1,n-1)(M(1))2∶=sup{E(n-1,n-1)(f)2∶f∈M(1)}.

(8)

首先得到關于Km(zf',tm)2的函數類的最佳逼近.

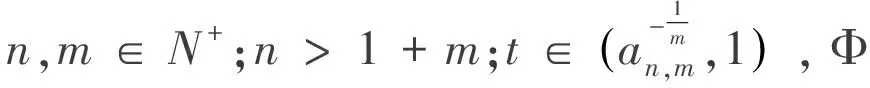
(9)

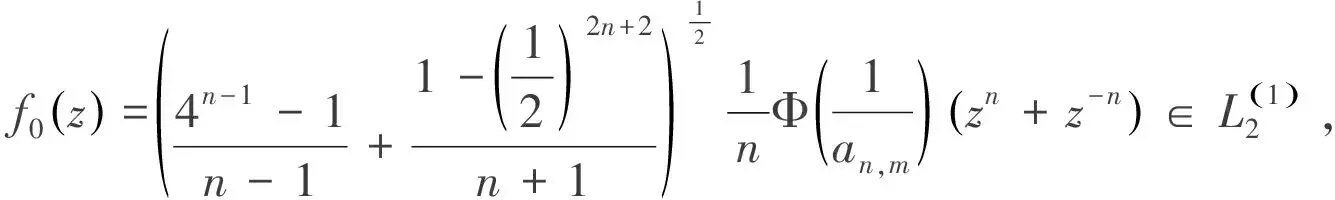
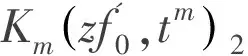
證畢.

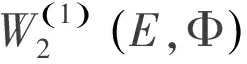
(10)

再由公式(8)，可以估計(10)式右邊的上界

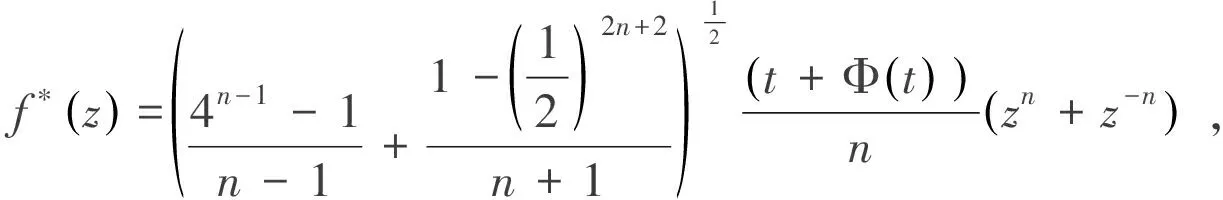
根據最佳逼近和(4)式知

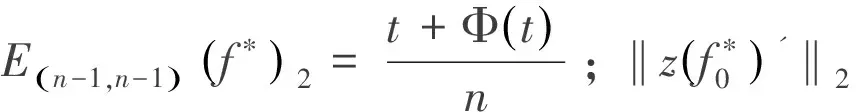
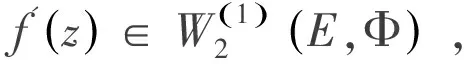
證畢.

4 函數類寬度的求解

定義5 令B是在L2空間下的單位球，假設Λ2n-1?L2的2n-1維子空間；Λ2n-1?L2的2n-1維余子空間；σ∶L2→Λ2n-1的線性連續算子；σ⊥∶Λ2n-1→L2線性連續算子；M是在L2下的凸對稱子集，則有

b2n-1(M,L2)=sup{sup(ε;εB∩Λ2n?M)∶Λ2n?L2}；

d2n-1(M,L2)=inf{sup{inf{‖f-g‖2∶g∈Λ2n-1}∶f∈M}∶Λ2n-1?L2}；

δ2n-1(M,L2)=inf{inf{sup{‖f-σf‖2∶f∈M}∶σL2∈Λ2n-1}∶Λ2n-1?L2}；

d2n-1(M,L2)=inf{sup{‖f‖2∶f∈M∩Λ2n-1}∶Λ2n-1?L2}；

Π2n-1(M,L2)=inf{inf{sup{‖f-σ⊥f‖2∶f∈M}∶σ⊥L2?Λ2n-1}∶Λ2n?L2}；

在希爾伯特空間中滿足

b2n-1(M,L2)≤d2n-1(M,L2)≤d2n-1(M,L2)=δ2n-1(M,L2)=Π2n-1(M,L2).

(11)

得到兩種函數類的寬度.

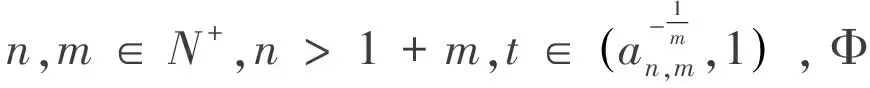
(12)

這里λ2n-1(·)表示b2n-1(M,L2)、d2n-1(M,L2)、d2n-1(M,L2)、δ2n-1(M,L2)、Π2n-1(M,L2)中任意一種寬度.

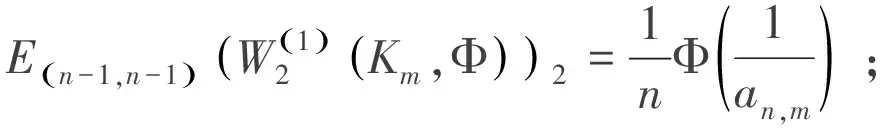
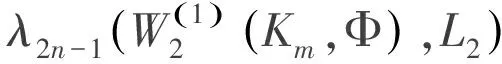
令2n維球體為

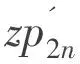
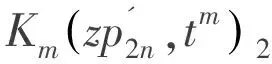
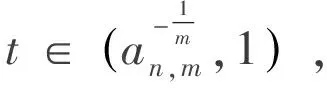
證畢.

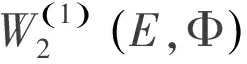
(13)

這里λ2n-1(·)表示b2n-1(M,L2)、d2n-1(M,L2)、d2n-1(M,L2)、δ2n-1(M,L2)、Π2n-1(M,L2)中任意一種寬度.

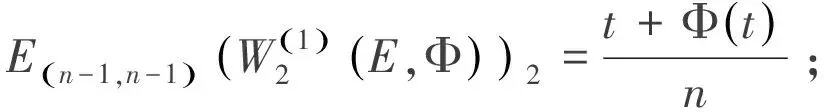
令2n維球體為

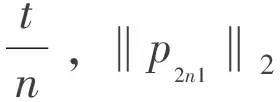
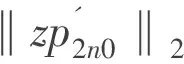
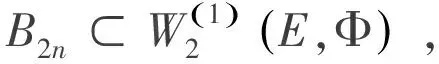
證畢.

5 總結

1)K泛函與最佳逼近E(n-1，n-1)(f)2的精確Jackson不等式；

2)E泛函與最佳逼近E(n-1,n-1)(f)2的不等式；

3)關于K泛函和E泛函的函數類的最佳逼近和2n-1維寬度.