基于松耦合法的π型主梁豎向渦振數值模擬

王向陽，張帥輝

（武漢理工大學 交通與物流工程學院，武漢 430063）

現代橋梁由于跨徑的增大以致結構剛度不斷下降，而結構的輕柔致使其對外部風環境十分敏感，目前風致橋梁振動問題已經成為大跨橋梁施工及運營階段抗風設計必須著重考慮的控制因素[1]。橋梁渦激振動是風與結構相互作用產生的一種振動形式，是由流經橋梁上下表面的流體所產生的交替脫落旋渦引起的限幅振動現象。當旋渦脫落頻率接近結構的某階自振頻率時就會發生共振，此時橋面振幅驟增嚴重影響行車安全以及降低結構疲勞壽命[2]。近幾十年來，由于橋梁渦振現象頻發，國內外學者對此展開了大量研究，從而在渦振的機理、影響因素以及抑振措施等方面取得一定的進展[3]。其主要研究方法逐漸從完全依賴傳統的風洞試驗過渡到數值模擬與試驗相結合，這一定程度上彌補了風洞試驗耗資大、周期長等不足，同時也說明數值模擬技術的可行性。國外學者Frandsen 等[4]基于有限元方法和動網格技術對大帶東橋進行渦激振動的全耦合模擬，其計算結果同其他研究數據相比較為吻合；Uenal 等[5]通過對一個近尾跡流場的計算分析發現4 種基于RANS（Reynolds Average Navier-Stokes）的湍流模型中SST（Shear Stress Transport）湍流模型模擬結果最準確；Daniels 等[6]采用大渦模型對矩形柱進行強迫振動模擬，得到了比較準確的計算結果；國內學者徐楓 等[7]將Newmark-β法寫入UDF（Users Defined Functions）并結合FLUENT 中的動網格技術成功觀測到柱體的鎖定、“拍”以及位移失諧的現象；陳文禮等[8]基于雷諾時均應力模型模擬得到了圓柱渦致振動的風速鎖定區域，且與試驗結果吻合較好；李永樂等[9]基于CFD（Computational Fluid Dynamics）和CSD（Computational Structural Dynamics）耦合的方法較好地模擬了方柱風致振動中的流固耦合效應。

以上研究的斷面形狀較為規則，且多為風洞試驗的驗證性研究。本文以π 形主梁斷面為研究對象，基于松耦合方法通過Newmark-β數值解法結合FLUENT中的二次開發接口來獲取斷面的渦激振動響應，采用“剛性運動區域+動網格區域+靜止網格區域”的方法分塊劃分網格[10]，通過網格光順和重構改善網格運動過程中的質量問題。在驗證該方法正確性的基礎上，建立一座擬建斜拉橋的有限元動力模型，根據獲取的動力特性參數對其進行風致渦振模擬，根據該模擬結果可初步判斷該橋梁的渦振性能，同時也可為后續的風洞試驗奠定一定基礎。

1 松耦合方法

松耦合法在不同學科中均有廣泛應用，對于氣動彈性問題，王少波等[11]通過CFD+CSD結合的方式給出基于松耦合法求解該問題的一般思路。針對本文中的渦激振動問題，首先在分析結構的豎向振動時將其看作是單自由度的彈簧振子系統，然后利用FLUENT 中的二次開發功能，將求解結構豎向動力方程的Newmark-β方法以及FLUENT中特有的宏命令寫入自編UDF 中與FLUENT 進行對接。開始計算時先求解每個時間步內系統的流體控制方程，并通過宏Compute_Force_And_Moment 提取結構上的升力，然后通過上述UDF中的Newmark-β數值方法求解在升力作用下結構的豎向運動方程從而得到位移、速度等物理量；再將在上一步得到的物理量通過宏DEFINE_CG_MOTIONG賦予給結構及周圍的動網格由此更新結構的運動狀態，待該時間步內計算收斂后進入下一時間步，由此不斷循環迭代直至所監控的物理量趨于穩定。具體求解思路如圖1所示。

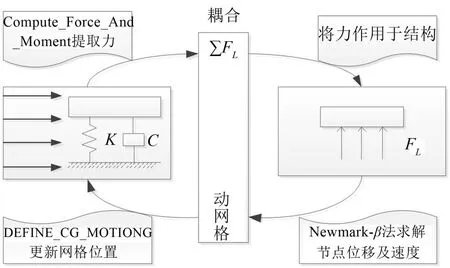
圖1 基于松耦合法求解豎向渦激振動示意圖

2 渦激振動的模擬驗證

為了檢驗本文基于松耦合方法求解豎向渦激振動數值模擬方法的正確性，選取文獻[12]中的矩形斷面進行渦激響應計算。其中矩形斷面高為0.075 m，寬為0.3 m，為與風洞試驗數據對比只考慮豎向自由度，因此將其簡化為只有豎向自由度的彈簧振子系統[13]。渦激振動模擬中的設計參數均取自文獻[12]，其中單位長度質量為1.362 kg，豎彎頻率fn為3.905 Hz，豎彎阻尼比為0.177%。

2.1 計算區域與網格劃分

為了使進口處流動能夠發展完全以及出口流完全流出，從而不對流動產生影響，要保證數值模擬的阻塞率小于3%[14]，因此將計算域大小取為18B×12B的矩形，速度進口邊界和上下對稱邊界距離矩形斷面形心6B，壓力出口邊界距離斷面形心12B，其中B為模型特征長度（B=0.3 m）。計算域以及邊界條件的設置如圖2所示，其中矩形斷面為無滑移邊界。

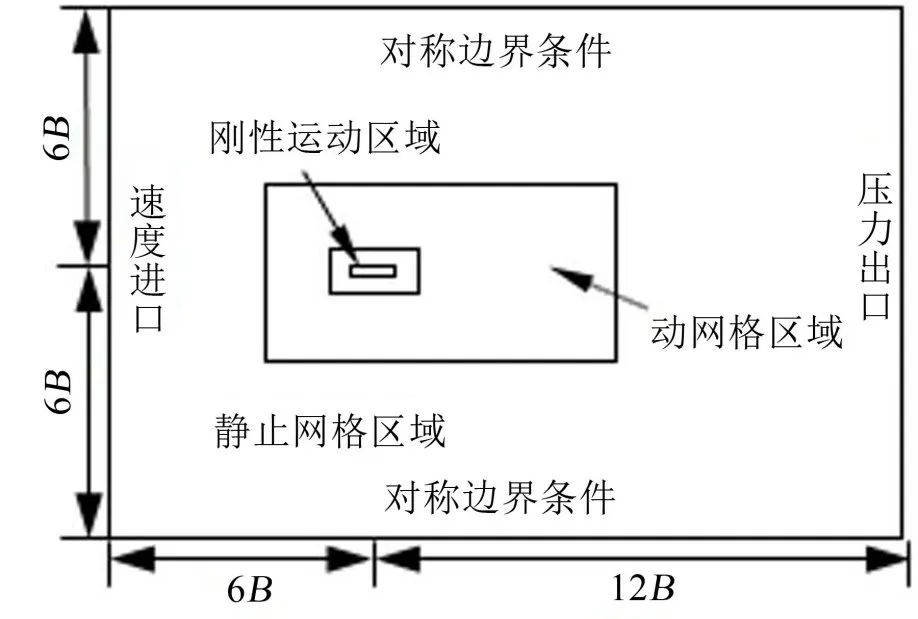
圖2 計算域及邊界條件設置

在劃分網格時考慮到梁斷面在運動過程中所導致的網格畸變、負體積等問題，采用分塊的方式將網格分為剛性運動、動網格以及靜止網格3 大區域。其中剛性運動區域距離梁斷面最近，設置較密的網格，該部分網格跟隨梁斷面一起運動，且為了能夠捕捉到氣流流經主梁斷面時發生的“分離”和“再附”現象，對主梁斷面設置邊界層網格；在動網格區域設置尺寸較大三角形網格來解決剛性域運動帶來的網格質量問題；靜止網格區域距離梁斷面最遠，對其采用漸變率較大的網格以提高計算效率，整個計算域的網格總數為46 893，其中第一層網格高度設為0.001B，近壁面網格劃分如圖3所示。

圖3 近壁面網格劃分

2.2 數值結果驗證分析

采用k-ωSST湍流模型進行豎向振動瞬態繞流計算，通過UDF 控制梁體，經過充分繞流后釋放梁體，分別對折算風速為4、6、8、8.5、9、9.5、10、12、14、16 共計10 個風速工況進行豎向單自由度的渦激振動計算，由于篇幅所限部分折算風速下的位移時程計算結果如圖4所示。

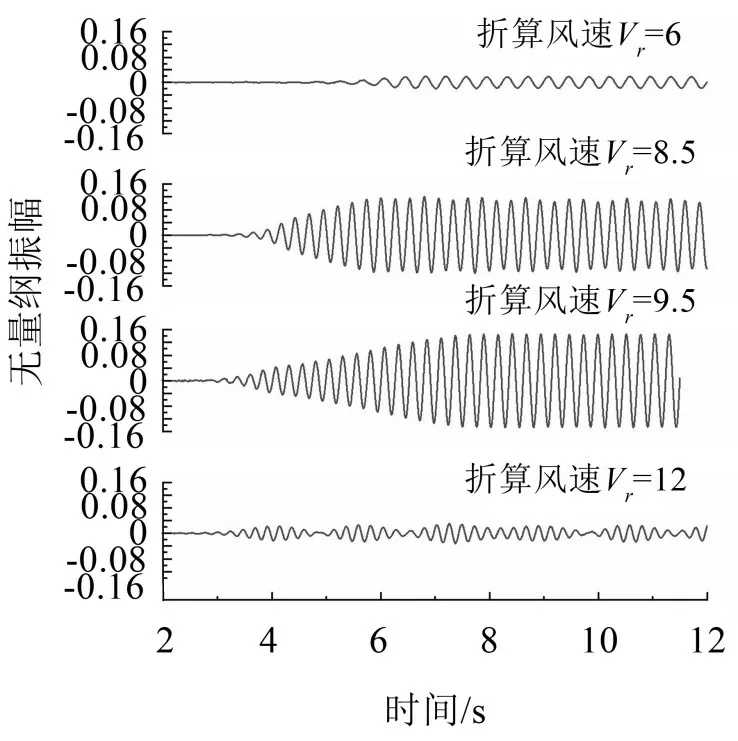
圖4 不同折算風速下矩形斷面位移時程曲線

由圖4可知矩形斷面在不同折算風速下的振動幅值差別很大，在Vr=6時振幅較小，在Vr=9.5時振幅達到最大，當風速增加到Vr=12 時振幅又減小，可見渦激振動時的風速在6～12之間。

圖5所示為無量綱振幅隨折減風速變化的折線圖，從圖中可以看出本文模擬結果中除渦振結束時的振幅有一定差異外，起振風速、最大振幅以及風速“鎖定區間”同文獻試驗數據吻合度較高；圖6所示為漩渦脫落頻率與結構固有頻率比（fs/fn）隨折減風速變化的折線圖，從圖中可以看風速在6～12 之間時的fs/fn值在1.0附近，此時漩渦脫落頻被結構頻率“捕獲”。以上結果驗證了本文求解豎向渦激振動問題數值模擬方法的可靠性，該方法可用于后續的分析。

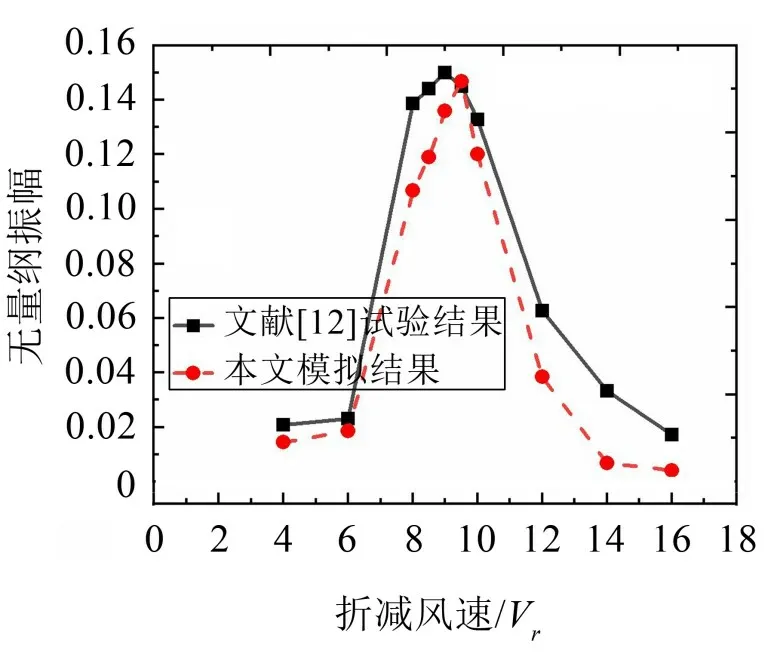
圖5 無量綱振幅隨折減風速的變化曲線

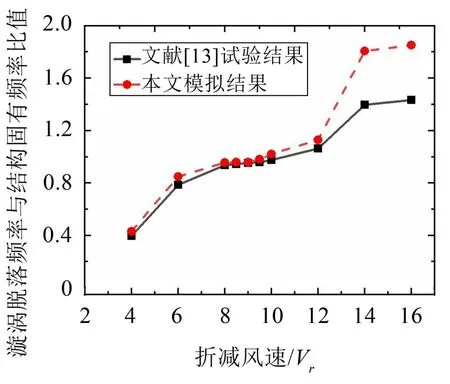
圖6 頻率比隨折減風速的變化曲線

3 漢江大橋渦激振動模擬

3.1 有限元模型建立及動力特性計算

某擬建漢江大橋橋型為雙塔雙索面組合梁斜拉橋，主橋立面采用對稱布置，主梁采用半漂浮體系。全橋的跨徑布置為（50+112）m+370 m+（112+50）m，主橋長度為694 m，主跨跨度為370 m，邊跨設置1個輔助墩和1個過渡墩，邊跨跨度為162 m，邊中跨比為0.437。橋面全幅寬28.3 m，橋面雙向橫坡的坡率為2%，π形主梁標準斷面如圖7所示。

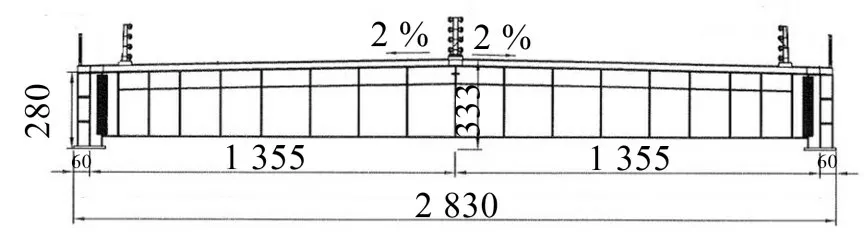
圖7 π形主梁標準橫斷面

建立該斜拉橋有限元動力模型的工作借助軟件ANSYS來完成。主梁采用單脊梁模式模擬，其中主梁、橋塔和橋墩采用BEAM188 梁單元，斜拉索采用LINK8 桿單元，二期與檢修車道等附屬設施采用MASS21質量點單元，全橋有限元模型如圖8所示。

圖8 漢江大橋有限元動力模型

表1中給出了橋梁豎彎、扭轉的1階自振頻率以及對應的等效質量等參數，與表1所對應的振型圖如圖9所示。

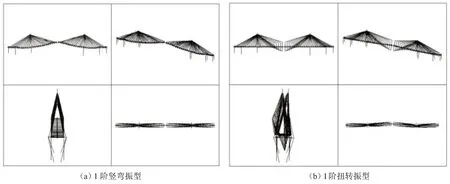
圖9 漢江大橋振型圖

表1 動力特性計算結果

3.2 單自由度豎向渦激振動模擬

對于渦激振動，文獻[15]中表明當扭彎基頻比大于1.4時難以發生彎扭耦合振動的情況，這時兩種渦振形式相互獨立。根據表1可知文中漢江大橋的扭彎基頻比為1.52，兩者基頻相差較大，且根據渦激振動的特點可知豎彎渦振會先于扭轉渦振發生，因此本文針對豎向自由度渦振進行模擬。

3.2.1 計算域及網格劃分

模擬時對主梁進行一定簡化，暫不考慮護欄等附屬設施，斷面幾何參數如表2所示，計算域的大小及邊界條件的設置同圖2中設置相同，網格劃分方式同2.1小節中一樣將網格分為剛性運動、動網格以及靜止網格3大區域，具體網格劃分如圖10所示，第一層網格高度為0.000 2B（B為梁寬）。數值模擬相關參數設置如表2所示，其中豎彎阻尼比取為0.79%。

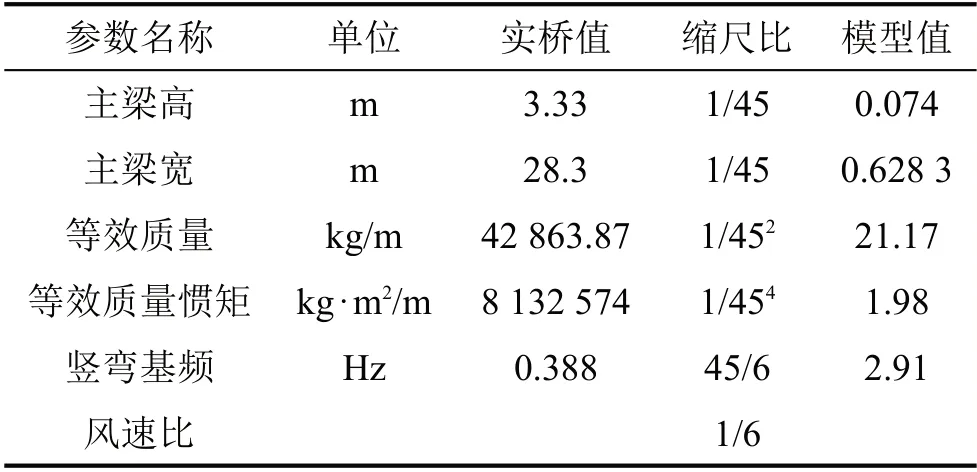
表2 模擬相關參數設置

圖10 π梁斷面網格劃分

3.2.2 豎向渦激振動模擬結果

先對主梁斷面進行靜止繞流模擬，數值計算時采用k-ωSST雙方程模型，通過Simplec算法求解耦合的速度場和壓力場，時間步長取為0.001 s。通過計算來流風速為2 m/s～5 m/s范圍內的St（斯托羅哈數）得到其均值為0.06，根據公式U=fnD/St估計發生最大渦振振幅時的來流風速在3.6 m/s左右，因此分別對來流風速為1.9 m/s、2.5 m/s、3.1 m/s、3.3 m/s、3.5 m/s、3.7 m/s、4.0 m/s、4.3 m/s、4.9 m/s的9個工況在0°風攻角下進行渦激響應計算。限于篇幅，本文只給出了渦振起振振幅、較大振幅、最大振幅和振幅開始減小時所對應風速下的位移時程曲線以及FFT（Fast Fourier Transform）變化頻譜曲線，如圖11至圖14所示。

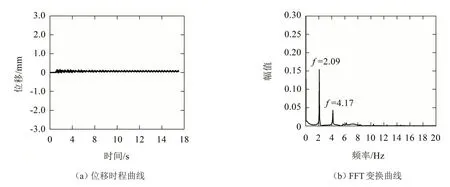
圖11 來流風速為2.5 m/s時的計算結果

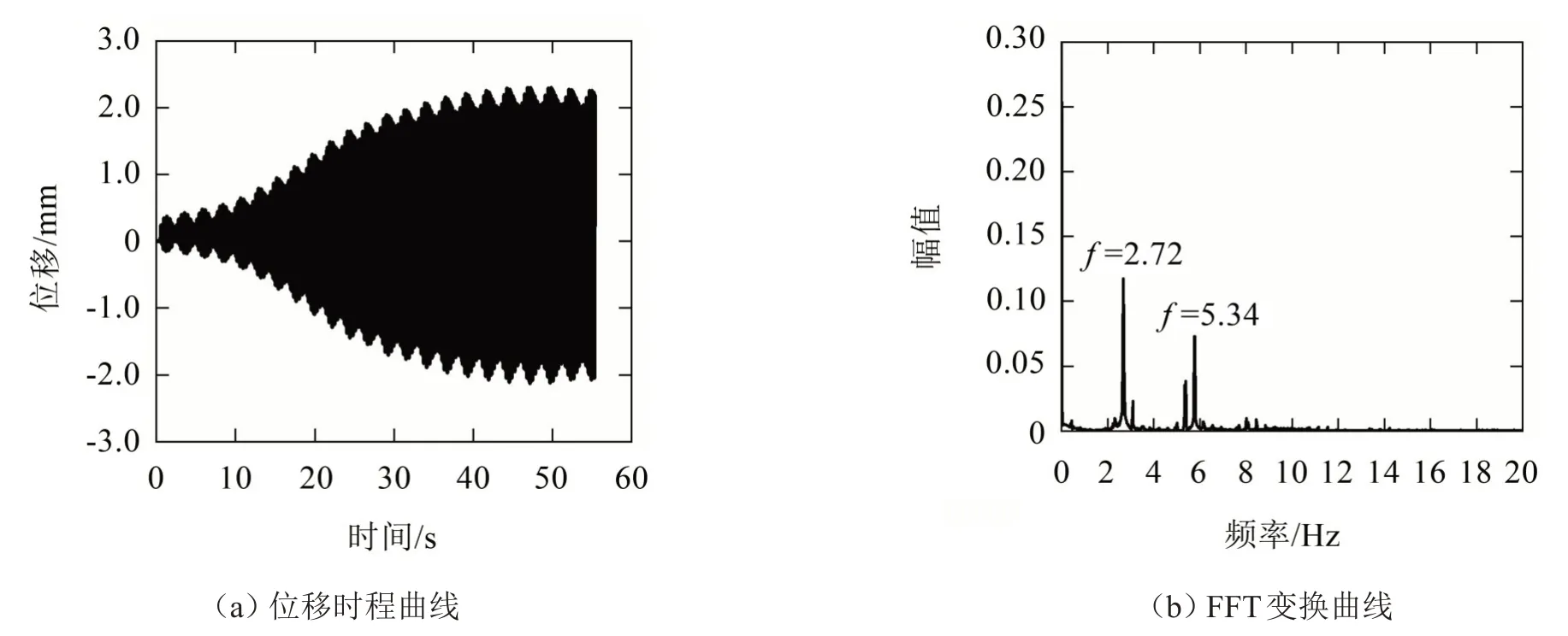
圖12 來流風速為3.3 m/s時的計算結果

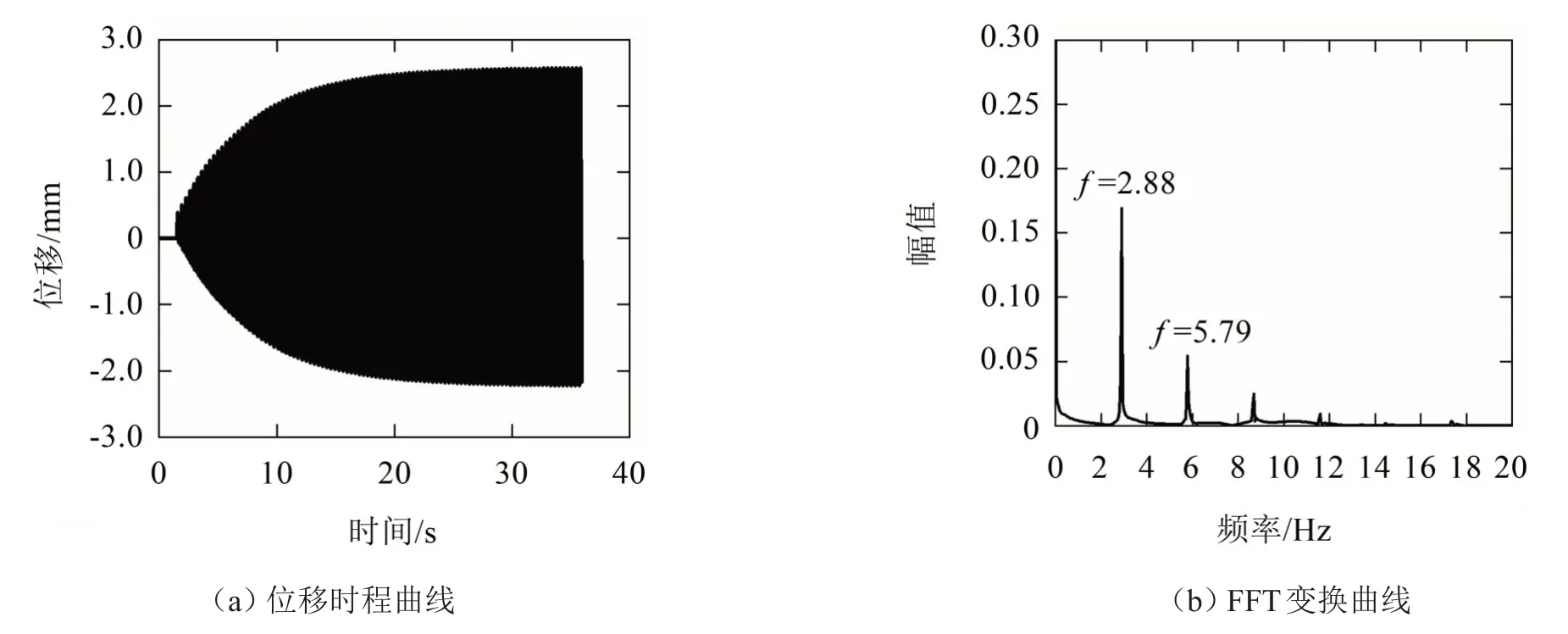
圖13 來流風速為3.7 m/s時的計算結果

如圖11至圖14所示，在不同風速下π梁斷面渦激振動幅值變化很大，在來流風速為2.5 m/s時振幅很小，對應梁斷面的旋渦脫落頻率（卓越頻率）為2.09 Hz，此時還未被結構自振頻率捕獲；當來流風速增大為3.3 m/s 時，梁斷面振幅迅速增大，渦脫頻率接近結構自振頻率，此時發生“鎖定現象”；當來流風速進一步增大到3.7 m/s時渦激振幅達到最大值，此時渦脫頻率與結構豎頻基本一致；當風速增大至4.0 m/s 時梁斷面的旋渦脫落頻率繼續增大，振幅回落到較小值，“鎖定現象”消失。

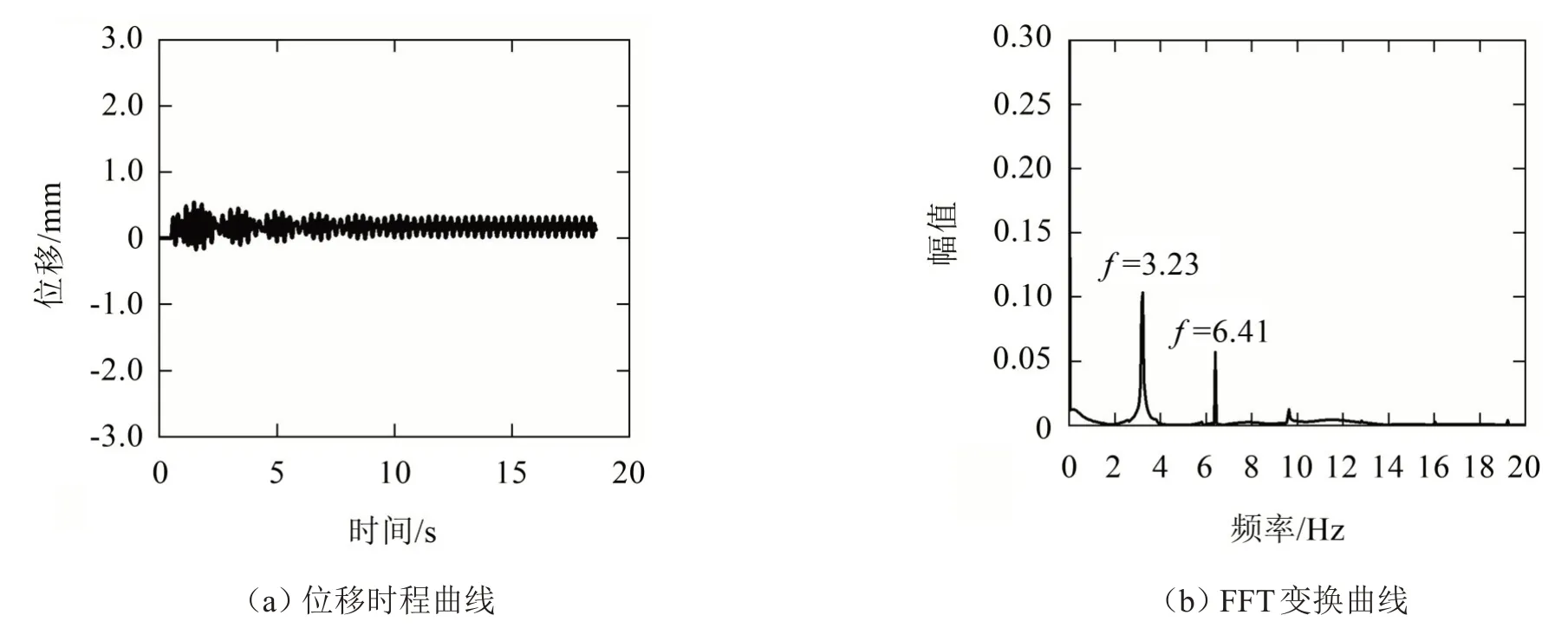
圖14 來流風速為4.0 m/s時的計算結果

圖15至圖16分別為梁斷面在1/45 縮尺下振幅隨風速變化的折線圖和旋渦脫落頻率隨來流風速變化的折線圖。

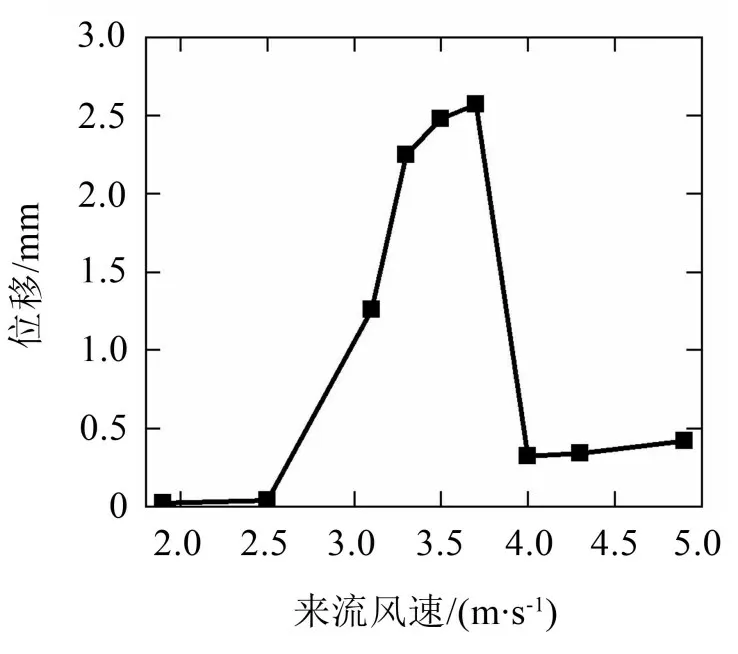
圖15 振幅隨風速的變化曲線

從圖15中可以看出，π梁斷面在2.5 m/s～4 m/s的風速范圍內振幅較大，發生渦激振動現象，在來流為3.7 m/s時振動幅值最大為2.57 mm；

從圖16可以看出，風速在3.0 m/s～4.0 m/s的區間內時旋渦脫落頻率變化很小且接近主梁豎向固有頻率，即發生了“鎖定現象”。

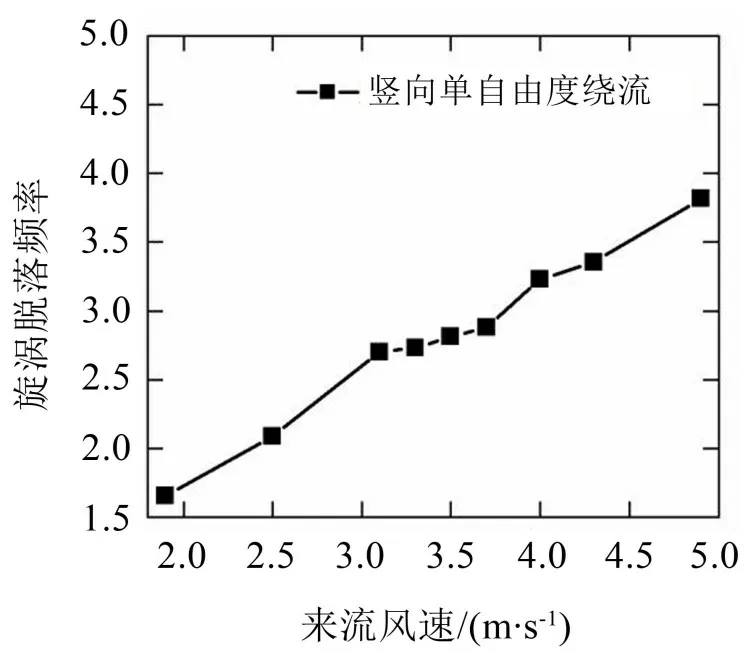
圖16 旋渦脫落頻率隨來流風速的變化曲線

圖17為來流風速為3.7 m/s 時π 梁斷面某一周期內的瞬時渦脫變化圖。

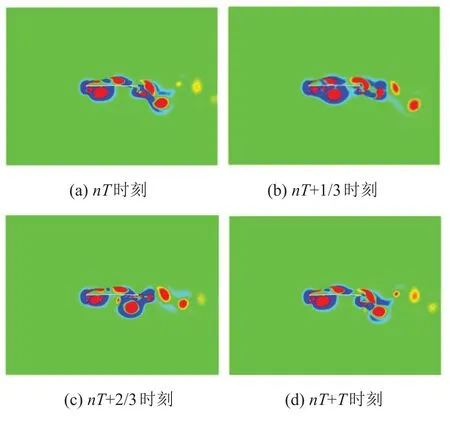
圖17 π梁斷面瞬時渦脫演化圖

從圖17中可以看出，在梁的不同位置處均有不同尺度的漩渦出現且主要產生自梁前緣的上下側以及梁后緣下側。對于梁前緣下側的旋渦，從圖17(a)中可以看出，在初始nT時刻剛生成的旋渦準備向下游移動；在nT+1/3時刻移動至梁1/2處；在nT+2/3時刻移至梁后緣并且此時梁前緣下側的旋渦已形成較大規模；在nT+T時刻已經脫離梁斷面向右下方移動，此時梁前緣下側的旋渦經過發展已具有足夠規模又開始準備移動，至此完成一個脫落周期。對于梁前緣上側以及后緣下側的旋渦而言，前者在經歷分離、再附后與后者形成交替出現在梁尾流區域的卡門渦脫。由以上分析可知，氣流在梁迎風面發生分離后分別在梁上下側的某些固定位置形成旋渦，旋渦不斷后移至梁背，此時梁背上側與下側的旋渦相互合并后在梁背風面形成上下不斷脫落的旋渦，從而導致主梁發生豎向的渦激振動。

4 結語

本文借助流體分析軟件FLUENT，基于松耦合方法通過嵌入Newmark-β法的UDF程序，求解某擬建漢江斜拉橋π 型主梁斷面的豎向渦激振動問題，得到如下結論：

（1）通過對寬高比為4 的矩形斷面的渦激振動模擬，證明了采用該模擬方法求解渦激振動問題的可行性和正確性。

（2）通過對9 個風速工況下的π 型主梁進行渦激振動模擬確定了“鎖定區間”，發現來流在2.5 m/s～4.0 m/s風速范圍內時主梁振動幅值較大，發生“鎖定現象”。

（3）根據對π 型主梁斷面某一完整周期內旋渦脫落過程的分析，發現在梁背風面不斷產生上下脫落的旋渦導致了π型主梁斷面的豎向渦激振動。