考慮波浪漂移力的漁船騎浪/橫甩計算和臨界區(qū)域規(guī)避

葉沈陽 陳思源 何 適 張寶吉

（1. 上海海事大學 海洋科學與工程學院 上海 201306； 2. 上海海事大學 商船學院 上海 201306）

0 引 言

船舶在隨浪或尾斜浪中航行時，波浪從船后方接近船尾，最終將船舶捕捉，船舶同波浪一起前進。此時，即使打出最大舵角也無法保持航向，此種現(xiàn)象稱為橫甩，橫甩時通常會有很大的橫搖角導致船舶傾覆。大量的海難事件表明，橫甩通常發(fā)生在一些中小型高速船上。因此，近年來IMO將騎浪橫甩列為二代完整穩(wěn)性中的1種失效模式。對于騎浪橫甩的研究首先是判斷該船型是否滿足 第1層和第2層薄弱性衡準，若不滿足，就要進行直接評估。在薄弱性衡準校核方面，國內(nèi)外的研究已很成熟，一系列軟件相繼出現(xiàn)。而對橫甩的直接評估，由于其機理復雜，研究者相對較少。

近年來，隨著人們對非線性動力學研究的不斷深入，將非線性動力學研究成果應用到橫甩的研究中成為可能。日本UMEDA最早開始研究船舶橫甩問題，隨后人們開始采用非線性動力學理論Melnikov法去研究騎浪問題。針對橫甩的直接評估，UMEDA等先后建立四自由度操縱性耦合方程，對橫甩現(xiàn)象進行數(shù)值模擬。于立偉等采用耐波性和操縱性統(tǒng)一理論建立了六自由度弱非線性運動模型，研究了騎浪橫甩的數(shù)值模擬問題，范佘明基于Z形試驗結果，采用六自由度操縱性模型對橫甩現(xiàn)象進行了預報。低頻慢漂運動會對船舶的運動狀態(tài)產(chǎn)生影響，張曉磊等在研究救助船的操縱性運動時考慮了波浪漂移力的作用。ZHANG等建立了三自由度操縱性模型，采用Rankine源法計算了二階波浪漂移力，對S175集裝箱船進行了回轉和Z形運動仿真。劉聰?shù)然谟嬎懔黧w動力學（computational fluid dynamics，CFD）法計算了DTC船型在斜浪作用下的漂移力。VADIM等基于CFD法建立了數(shù)值波浪水池，將波浪漂移力加入到波浪力中，研究了ONR船的騎浪橫甩問題，并通過模型試驗進行了驗證。

本文在總結前人研究成果的基礎上，以四自由度操縱性方程為基礎，將經(jīng)驗公式計算的波浪漂移力加入到波浪力公式中，研究漁船在不同波長船長比，不同舵角下的運動規(guī)律，并和沒有考慮波浪漂移力的計算結果進行比較；再以此數(shù)據(jù)為基礎，研究船舶航行臨界區(qū)域的預測方法，判斷航行的臨界速度和航向角，并和已有的實驗結果進行比較，進而提出船舶航行規(guī)避危險區(qū)域的指導性意見和建議。

1 船舶四自由度運動模型

本文使用的是船舶的四自由度運動模型，坐標系和方程如下：

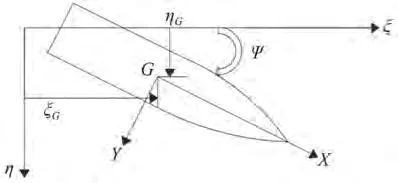
圖1 操縱性方程運動坐標系

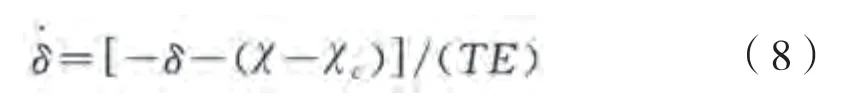
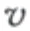
控制方程中，波浪力的計算方法參考文獻[17]。

基于船舶騎浪橫甩第2層薄弱性衡準，提出橫甩直接數(shù)值評估衡準數(shù)的計算公式：

2 漂移波浪力的計算方程

對四自由度MMG操縱性模型進行擴展，在縱向波浪力、橫向波浪力和艏搖力矩中加入對應方向的波浪漂移力經(jīng)驗公式。

從6個公式中可以看出，除了艏搖角以外，其他量都是船本身或波浪本身設定的常數(shù)，因此式中都是以為自變量計算的。

3 騎浪/橫甩在隨浪和尾斜浪下的 直接模擬

選有義波高=1.5 m、1.5 m、2.5 m和對應的為過零周期7.5 s、7.5 s、8.5 s 3種發(fā)生概率最大的隨浪和尾斜浪不規(guī)則波為算例，船的初始艏搖角取0°~30°，臨界弗勞德數(shù)（）取0.1~0.5；改變船的舵角和初始速度，以ITTC ship A2漁船作為研究對象，計算漁船在規(guī)則波下航行時發(fā)生騎浪橫甩的規(guī)律，繪制圖像。漁船的參數(shù)如表1所示。

表1 漁船船型主尺度和船型參數(shù)

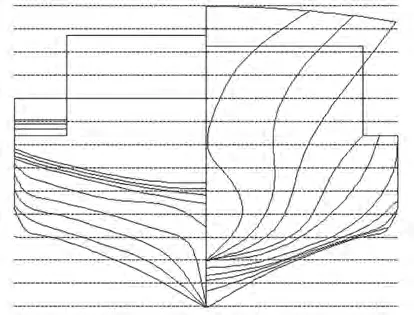
圖2 ITTC ship A2漁船橫剖面型線圖

計算臨界從0.1～0.5，間隔變化0.01，初始艏搖角從1°~30°，間隔為1°，共計算41×30= 1 230組數(shù)據(jù)，并且針對波長船長比、波陡和臨界轉速等同樣進行對照實驗。圖3是未加入和加入波浪漂移力時漁船運動狀態(tài)變化關系圖。

圖3 漁船的運動狀態(tài)變化

由圖3可知：加入波浪漂移力之后，在初始艏搖角較小時，漁船的運動狀態(tài)主要是周期性運動和騎浪，但當角度增大后，伴隨著臨界的增大，船舶開始出現(xiàn)傾覆，并且隨著角度越大，傾覆的比例越高。與未加入波浪漂移力的情況進行對比，可以發(fā)現(xiàn)加入漂移力后運動的走勢變化大致與未加入時一致，不過周期性運動和騎浪的分界線在0.34上，較未加入波浪漂移力的情況更高，說明在加入波浪漂移力后，船的運動狀態(tài)更穩(wěn)定；并且船在已計算的數(shù)據(jù)中沒有發(fā)生橫甩，傾覆概率也更小，因此橫甩衡準值為0。

固定初始艏搖角為0°，保持臨界螺旋槳轉速為4.125 r/s，改變波長船長比和波陡進行漁船運動仿真。

初始艏搖角為0°時，漁船的運動狀態(tài)如圖4所示。由圖4可知：加入波浪漂移力之后，漁船的周期運動和騎浪運動范圍增加，傾覆范圍減小。

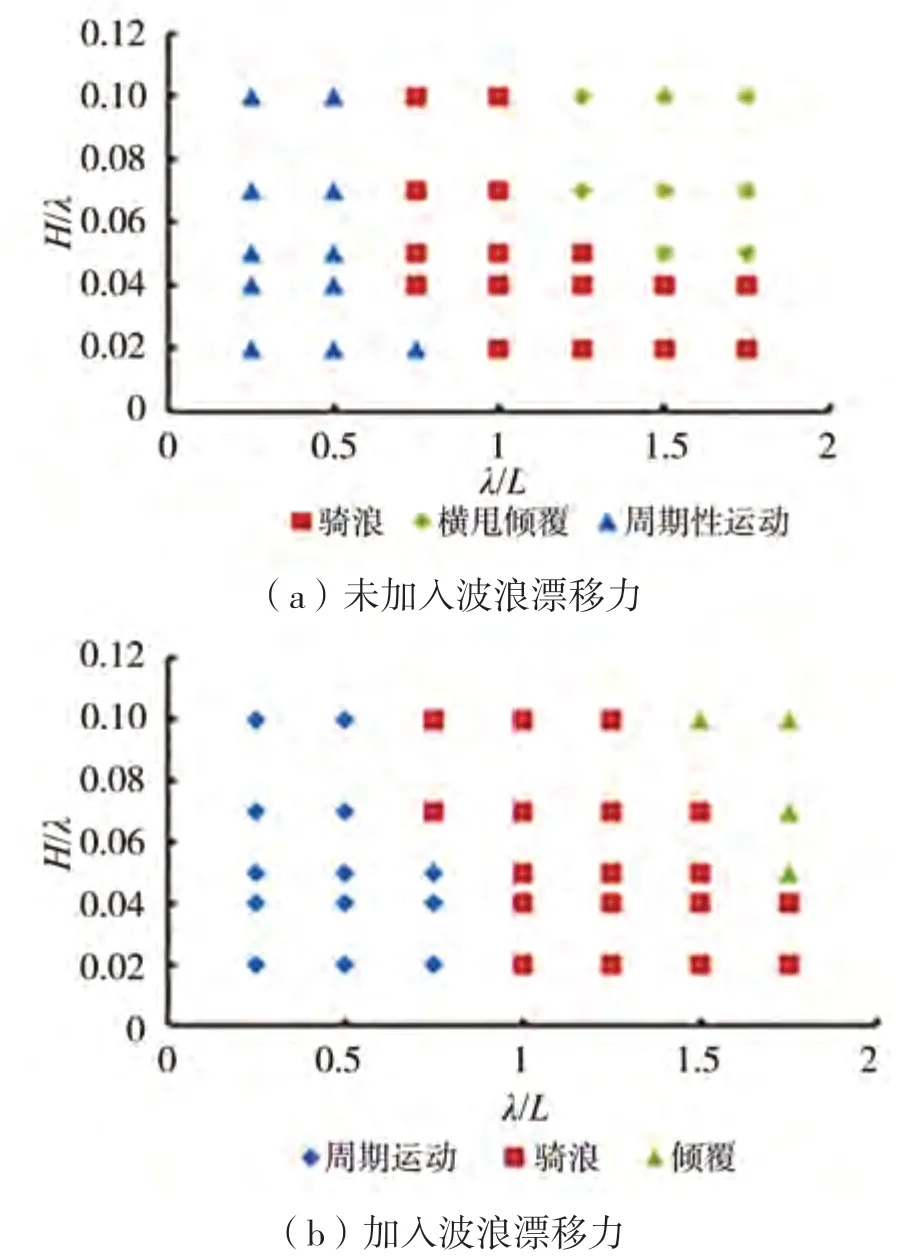
圖4 初始艏搖角為0°，漁船的運動狀態(tài)

初始艏搖角為-15°時，漁船的運動狀態(tài)如下頁圖5所示。由圖5可知：加入波浪漂移力之后，漁船的運動狀態(tài)幾乎全部變?yōu)閮A覆，說明加入波浪漂移力之后，初始艏搖角對漁船的運動狀態(tài)影響極大。

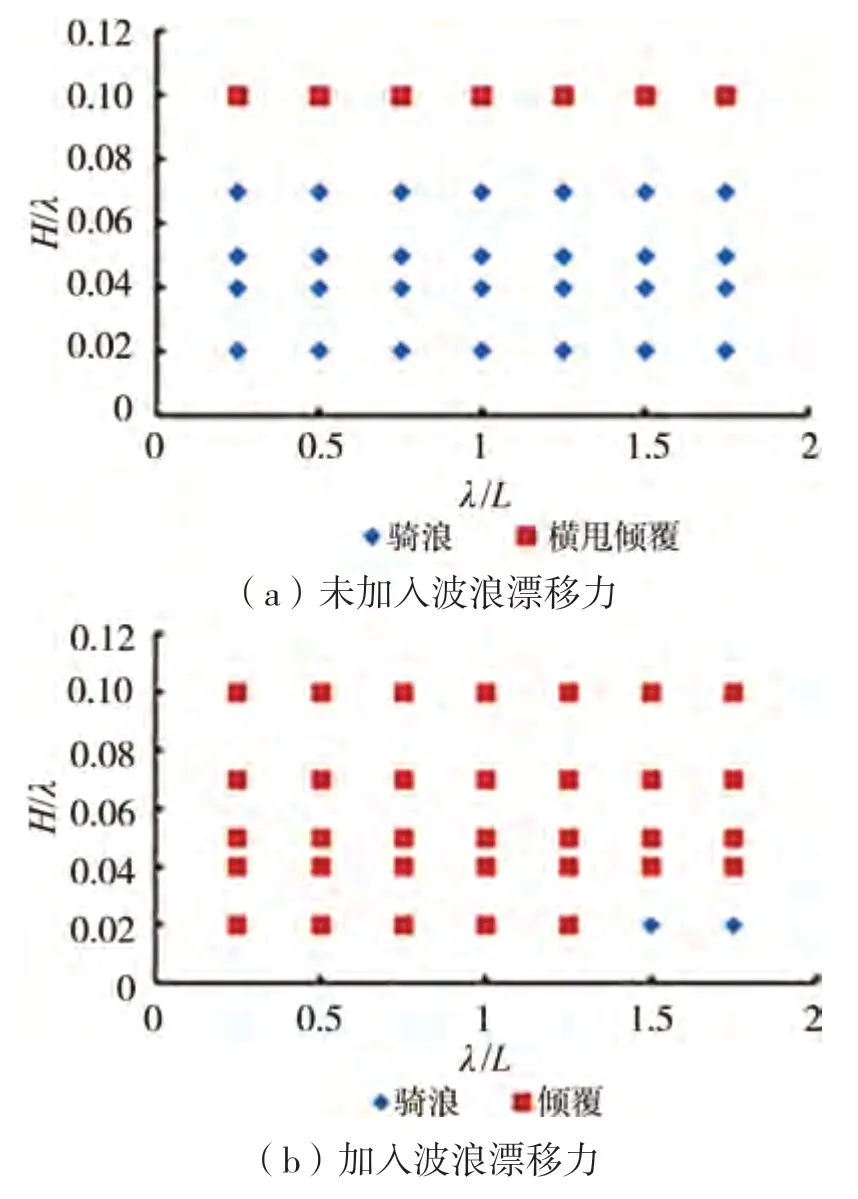
圖5 初始艏搖角為-15°，漁船的運動狀態(tài)

綜合以上計算結果，可得出以下結論：

（1）周期性運動與變化的邊界由原來的臨界0.3變化為0.34，在波陡和初始艏搖角都較小的情況下，不穩(wěn)定區(qū)域更小。

（2）受到波長船長比、波陡變化的影響與無波浪漂移力類似，不過周期性運動的范圍更大。

（3）更容易受到初始艏搖角的影響，在經(jīng)過某個臨界值后，船的不穩(wěn)定性會極大增加。

總體來說，加入波浪漂移力會使在低波陡等參數(shù)下的運行狀態(tài)更平穩(wěn)，而在高波陡高轉速的狀態(tài)下更危險。

4 騎浪/橫甩臨界區(qū)域和規(guī)避

4.1 背景介紹

由前面的數(shù)據(jù)分析可以得出：影響航行最重要的因素有波參數(shù)、航速和浪向角，而波的因素是無法人為改變的，能夠改變的只有航速和浪向角；確定船在不同速度下和浪向角的關系，從而確定不同程度的危險性變得尤為重要。本節(jié)將研究船舶航速與波浪、與船夾角直接變化規(guī)律，從而確定船在航行中的臨界區(qū)域和危險區(qū)域。

4.2 模型參數(shù)設置

將船的遭遇波設置為規(guī)則波，計算ITTC ship A2漁船在波長船長比為1、波陡為1/15時，等效浪向角的變化，其中船舶航速和船長開根號比值的變化范圍是0.8~3，間隔為0.2，等價于速度由2.4 m/s增至9.1 m/s，自動航向角的范圍取-45°~ 45°，間隔為5°，共計算12×19=228組數(shù)據(jù)。圖6顯示了漁船隨航速、浪向角的運動狀態(tài)變化。

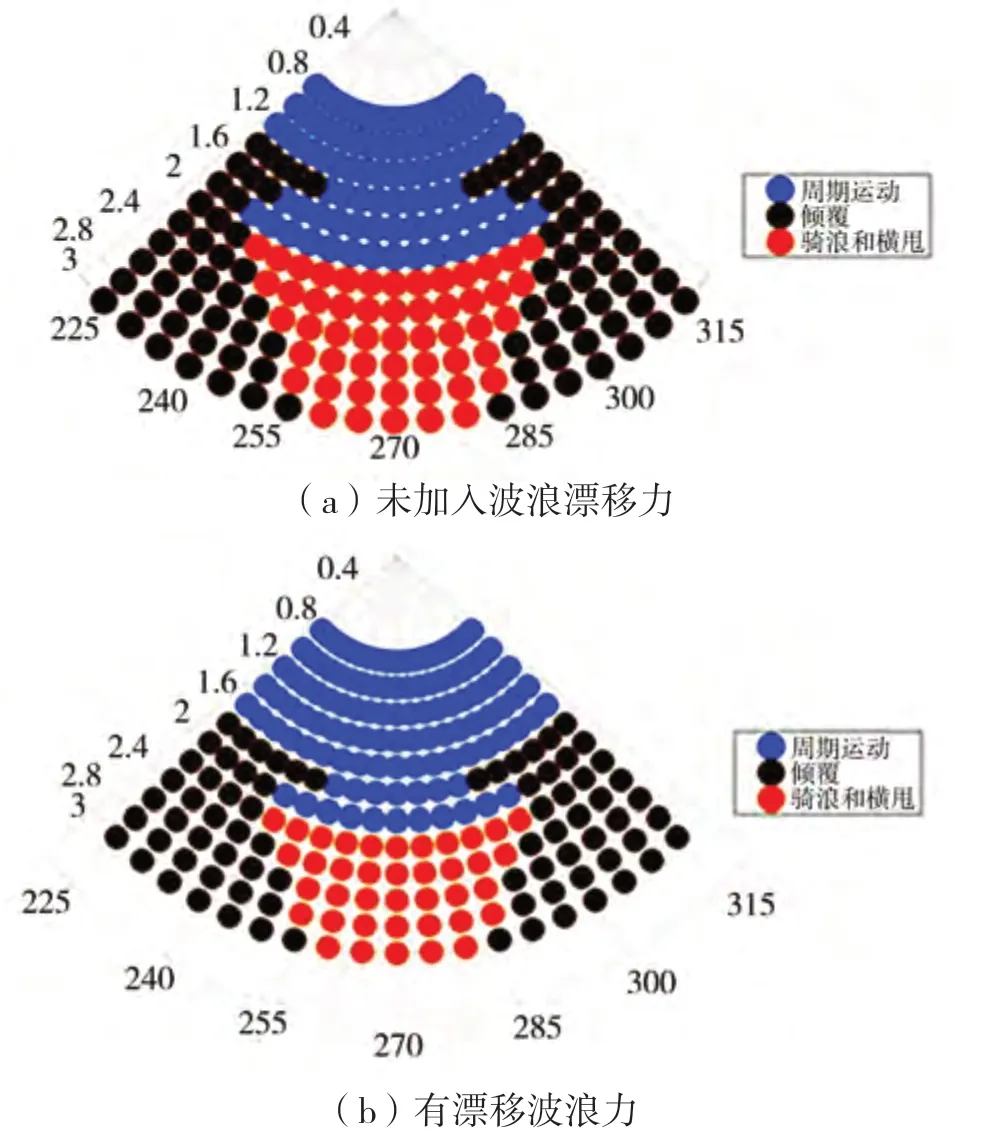
圖6 漁船隨航速和浪向角的運動狀態(tài)變化

如圖6（a）所示，船處在極坐標的原點處，船首方向與圖中的270°角方向相反，即朝向90°。極軸上的數(shù)字表示的是船舶航速和船長開根號的比值，中線與不同線段的夾角就是船與浪之間的夾角，即浪向角。可以看出，周期性運動的范圍主要集中在比值＜2并且浪向角較小的范圍內(nèi)。在浪向角較小、比值稍大的區(qū)域（如1.4左右），開始出現(xiàn)傾覆。當比值＞2之后，小浪向角范圍內(nèi)的周期性運動全部轉變?yōu)轵T浪或者橫甩，分界線上的變化非常迅速。傾覆主要集中在浪向角大的部分，不過從圖上的變化趨勢來看，隨著比值越來越高，傾覆的比例也會越來越大。

圖6（b）是加入波浪漂移力的變化，周期運動的范圍略有增大，比值在1.4左右的位置也沒有發(fā)生傾覆。騎浪和橫甩的范圍因為周期性運動的范圍增大而減小，傾覆的變化規(guī)律則沒有變化，加入波浪漂移力后的穩(wěn)定性與之前的討論相匹配。

4.3 與實驗值對比

日本船舶互保協(xié)會（Japan P & I club）對船在不同浪向角和不同船速時的騎浪橫甩區(qū)域作出了完整的定義。圖7為實驗中定義的臨界區(qū)域和危險區(qū)域。

圖7 實驗中定義的臨界區(qū)域和危險區(qū)域

由圖7可知：圖中的實驗浪向角與仿真的范圍一樣，從-45°～45°，極徑上的坐標同樣是航速和船長開根號的比值。圖中比值在2～2.2的區(qū)間稱為邊際區(qū)域，表示船處于發(fā)生或不發(fā)生騎浪橫甩的區(qū)域。在這個區(qū)域內(nèi)，船的速度有可能發(fā)生急劇的變化，而這些變化有可能導致騎浪橫甩甚至傾覆。而比值＞2.4的紅色區(qū)域為危險區(qū)域，表示船一定會發(fā)生騎浪和橫甩。

與圖6（a）進行對比，在沒有考慮波浪漂移力的情況下，將圖6（a）中比值從1.4～2的區(qū)域視為同時存在發(fā)生傾覆和周期運動可能性的臨界區(qū)域。實驗中的臨界區(qū)域明顯大于圖6（a）中的臨界區(qū)域，因此會發(fā)生騎浪橫甩和傾覆的危險區(qū)域也比實驗中的更大。而在圖6（b）中，臨界區(qū)域則是在比值為1.8～2的區(qū)域，這與實驗值得出的結果更為相似。因此，在加入了波浪漂移力后，使用MMG操縱性方程模擬出的結果可以與實驗值相匹配。

日本船舶互保協(xié)會基于實驗值以及觀察數(shù)據(jù)得出了2個用以計算臨界區(qū)域和危險區(qū)域的公式，公式如下：

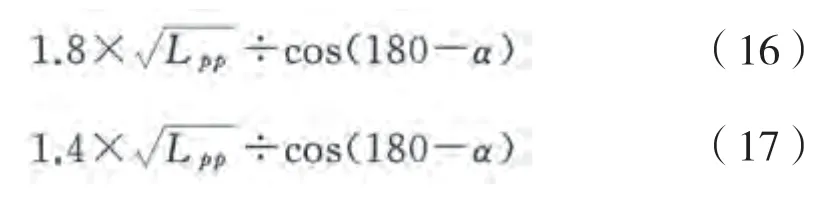
上面2個公式分別計算了速度的臨界區(qū)域和危險區(qū)域邊界，范圍都是225°～315°，等價于浪向角-45°～45°。以ITTC ship A2漁船為例，船長為 34.5 m，使用公式計算出船的速度和浪向角發(fā)生騎浪橫甩的臨界區(qū)域和危險區(qū)域的2條邊界曲線，繪制成圖像，如圖8所示。

圖8 公式繪制的曲線與仿真對比

圖8與圖7不同的是，在不加入波浪漂移力的情況下，2條邊界曲線與仿真的區(qū)域擬合程度更高，加入波浪漂移力的模擬卻相對降低了精確度。綜合實驗的區(qū)塊圖和規(guī)范準則的2條公式可以得出結論：即使2種對比上存在著一定的不同，在大致的范圍上仍然是一致的，因此，使用MMG操縱性模型仿真所計算的區(qū)域圖仍具有一定的參考性。

4.4 規(guī)避方法討論

船在航行時會遭遇多種多樣的情況，本文僅針對船在騎浪橫甩方面的危險性做出規(guī)避可能危險區(qū)域的模型。

船在航行時遭遇危險區(qū)域時一般選擇2種方式規(guī)避：第1種是增加航速，快速駛離危險，但是危險區(qū)域的范圍以及危險性都難以測定，加速所產(chǎn)生的危險甚至會加劇，因此，該方法只存在于理論上，難以實踐；第2種就是通過減速來降低危險，穿過危險區(qū)域，此方法更安全，保險性和可行性更高。

規(guī)避騎浪橫甩的模型如下：

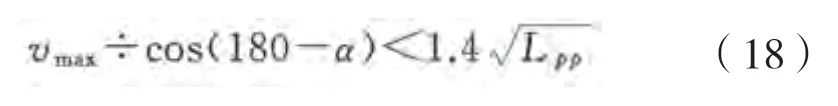
只通過調整浪向角來規(guī)避的模型如下：

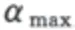
式中：角度和航速都是自變量，同時變化使規(guī)避的方式更加多樣化，能夠應對的情況也更多。

5 結 語

本文以四自由度操縱性方程為基礎，將經(jīng)驗公式計算的波浪漂移力公式加入到波浪力公式中，模擬漁船在不同波長船長比下的運動規(guī)律，通過和沒有加入波浪漂移力的計算結果對比，證實了考慮波浪漂移力時船舶的運動狀態(tài)將會更平穩(wěn)。此外，文中還研究了臨界區(qū)域的預測，判斷船在航行時的安全速度和穩(wěn)定角度。并將仿真結果和日本船舶互保協(xié)會的實驗數(shù)據(jù)和規(guī)范公式所給的界限進行對比，提出規(guī)避危險區(qū)域的指導意見。