基于軌道動態模型的星間鏈路測距隨機誤差測試方法

胡帆 尹卿 李振東 于澎 方凱 白力舸

(北京空間飛行器總體設計部，北京 100094)

衛星作為星座內的節點，精確確定其在星座內的相對位置是維持穩定星座構型的基礎，也是保障通信鏈路物理層穩定性和可靠性的基礎。由于在軌工作條件下衛星之間通信距離較遠，目標衛星在接收具有多普勒效應的星間測距信號時，往往在星上預設通信雙方的軌道信息，并實時計算輔助捕獲信息，以便盡量提升信號捕獲鎖定效率。相對運動中細微的時間檢測偏差，將導致目標衛星在接收捕獲信號時的測距誤差大幅增加，因此，在軌道動態條件下衛星相對距離準確度(即測距隨機誤差)的精確測量是衛星測距功能地面測試的難點。

在實際測試過程中，被測衛星作為接收端需要測試設備模擬與之通信的其他目標衛星發射信號，通信信息及測距信息調制于發射信號上，被測衛星使用輔助捕獲信息對接收到的測距信號進行解析，恢復測距信息。測試設備模擬的通信目標與被測衛星位置會相對變化，當前測試所涉及的位置變化場景主要有靜態場景、線性動態模擬場景、三角波動態模擬場景、正弦波動態模擬場景等。上述場景針對單臺設備的動態接收性能具備一定的模擬驗證能力，但在整星狀態下，衛星實際在軌運動時的軌跡會根據其他分系統提供的參數變化，靜態場景等對衛星在軌實際工作性能進行預示仍存在一定的不確定性。因此，研究地面測距模擬理論值的準確度，是提高測距隨機誤差測試結果準確性的重要途徑。

現有國內外測距隨機誤差測試主要集成于星間鏈路測試平臺,用于對星間鏈路和星地鏈路的測距隨機誤差、測距一致性等指標進行驗證。國外全球導航衛星系統(GNSS)星間鏈路測試平臺的研究項目種類多，各有側重。GNSS多星座模擬器(NAVYS)是針對GNSS的星座模擬設備，將包含獨立的衛星軌道參數、衛星時鐘、衛星天線方向圖、功率參數、波形、偽隨機碼和多徑傳輸方案等的完整配置端口提供給用戶，能夠對現有的星座及未來將會有的GNSS星座信號進行全方位仿真模擬[1]。伽利略衛星信號測試設備(GSVF)專用于衛星導航系統模擬測試，可對計劃中的伽利略衛星導航信號和信息結構性能進行評估[2-5]。國內導航系統模擬平臺側重于其他衛星導航電文對被測衛星星歷等的影響，能夠將被測衛星的導航工作狀態進行系統性的測試[6]；衛星網絡半實物仿真環境可對衛星網絡進行建模，在網絡層模擬衛星網絡的拓撲結構、衛星軌道運行帶來的動態拓撲變化，以及空間電磁信號傳輸導致的長時延、高誤碼率等空間環境特點，同時為網絡管理提供虛擬的對象[7]。現有測試平臺在進行動態測距隨機誤差功能測試時，采用的測試方法并未對軌道動態條件下地面距離模擬理論值的準確度進行深入分析。

本文提出基于軌道動態模型的星間鏈路測距隨機誤差測試方法，以提高對星間測距精度的測試能力。根據軌道六根數對軌道動態條件下的星間距離進行理論分析；針對運動中衛星的多普勒效應，提出軌道動態模型，模擬被測衛星以外衛星的星間鏈路距離動態信號，在被測衛星接收信號后進行測距計算；通過分析衛星地面測距模擬理論值的準確度影響，提出被測衛星的星間測距隨機誤差計算方法；將軌道動態星間測距隨機誤差測試方法應用于測試系統設計，進行工程驗證。

1 星間距離理論分析

在軌道動態條件下計算被測衛星與通信目標衛星之間的相對位置關系時，可將衛星抽象為質點，在地心第一坐標系OXYZ中可以根據軌道六根數對t時刻衛星位置坐標(x,y,z)進行計算[8]。

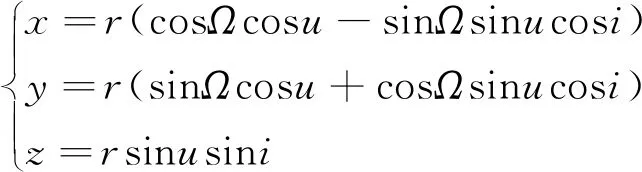
(1)

式中：r為地心距；Ω為升交點赤經；u為緯度幅角；i為軌道傾角。

在地面測試過程中，采用地面測試設備模擬衛星發出經過距離延遲產生的星間鏈路距離動態信號。其原理為：在發射信號時根據仿真計算獲得星間距離值進行相應的延遲，例如某時刻t，星間距離為d，則時刻t的星間鏈路信號延遲d/c再發射，其中，c為光速。

2 星間距離動態信號的地面模擬

設在測試時間段內{t1,t2,t3,…,tN}時刻仿真產生的星間距離分別為{d1,d2,d3,…,dN}，星間鏈路信號生成模塊產生的{t1,t2,t3,…,tN}時刻星間鏈路發射信號模擬星間距離的影響，由星間鏈路信號生成模塊對其分別進行時間延遲后發出，最終星間鏈路發射信號調整為{t1+d1/c,t2+d2/c,t3+d3/c,…,tN+dN/c}，使發出的星間鏈路信號攜帶軌道動態距離信息。星間鏈路接收機進行接收測距的時候，仍在默認的{t1,t2,t3,…,tN}時刻進行采樣測距，獲得的測距值即帶有星間距離信息，并疊加有自身設備測距隨機誤差。其中，N為測試時間段內采樣個數。

衛星在軌相對運動產生多普勒效應的同時，也伴隨著星間絕對距離的變化，表現為星間信號傳輸時延的變化。星間鏈路距離動態信號發射設備組成如圖1所示。其中，衛星軌道仿真計算模塊根據輸入的衛星軌道參數對星間距離進行實時仿真計算。

圖1 星間鏈路距離動態信號發射設備組成

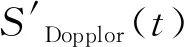
注：(t)為1級調制后通信支路；(t)為1級調制后測距支路；Δt為每間隔T0插入的時延。

3 星間測距隨機誤差計算方法

衛星進行星間測距時，會將實際發射時刻為{t1+d1/c,t2+d2/c,t3+d3/c,…,tN+dN/c}的信號默認為{t1,t2,t3,…,tN}時刻發射，因此進行接收采樣測距后帶有星間距離信息。設測距時刻為{t1′,t2′,t3′,…,tN′}，測距值為{r1,r2,r3,…,rN}，該測距值覆蓋了衛星的在軌真實工況，變化范圍較大，需要應用計算距離動態測距值的隨機誤差方法。

星間鏈路接收機測得的實時測距值及其組成部分可以表示為

r(t)=c(τs+τr)+L+d(t)+Δρ+v(t)

(2)

式中：r(t)為t時刻衛星軌道動態偽距測量結果，m；τs為星間測距測試設備發射通道時延，s；τr為衛星測距設備接收通道時延，s；L為測試電纜長度，m；d(t)為t時刻軌道動態條件實時仿真距離值，m；Δρ為地面測試設備和衛星之間的鐘差；v(t)為星間鏈路接收機測距隨機誤差。

以上組成部分中，c，τs，τr，L均為常量，在同源測試的情況下，Δρ也為常量，均不影響測距隨機誤差的計算，所以僅需要對r(t)-d(t)取標準差估計，就可以得到v(t)的估計值。因此，可以將距離動態測距值{r1,r2,r3,…,rN}減去測距時刻星間鏈路距離動態信號發射設備仿真計算產生的對應時刻星間距離值，獲得減后序列。設測距時刻{t1′,t2′,t3′,…,tN′}對應的仿真星間距離為{d1′,d2′,d3′,…,dN′}，則減后序列為{r1-d1′,r2-d2′,r3-d3′,…,rN-dN′}，該序列包含測距值觀測數據殘差，對該序列求標準差，即得到星間鏈路接收機的測距隨機標準差估計為

(3)

式中：i=1,2，…，N。

4 測試方法驗證

整個星間鏈路測距隨機誤差測試系統組成如圖3所示。其中：衛星軌道仿真計算模塊和星間鏈路信號生成模塊組成前文所述星間鏈路距離動態信號發射設備，它與測距隨機誤差計算模塊共同組成了地面測試設備，測距隨機誤差計算模塊負責完成將實時測距值序列減去對應時刻的仿真實時距離值，并完成標準差計算，從而完成測距隨機誤差計算。需要說明的是，本文采用的是同源測距方法，即地面測試設備與被測衛星使用的是同一個時鐘信號基準，即雙方的秒脈沖和用于產生測距信號的時鐘是完全同步的。如果采用非同源測試方法，則需要在圖3中增加鐘差測量設備，且式(2)中的實時測距值除了要減去仿真實時距離值，還要減去實時鐘差。

圖3 星間鏈路測距隨機誤差測試系統組成

采用本文方法對某衛星的星間鏈路測距隨機誤差進行測試。此衛星的星間鏈路測距信號體制為：以0或者t0整倍數時刻處為起始時刻，每個t0為1個時隙，前t0/2發射、后t0/2接收，或者前t0/2接收、后t0/2發射，具體發射與接收順序，由地面發送時隙表指令進行配置，本文以衛星的星間鏈路接收機在每個t0時隙的后t0/2進行采樣測距為例進行描述，衛星的具體采樣測距時刻為t0時隙的11/12t0處，對應的地面測試設備則在每個t0時隙的前t0/2發射測距星間鏈路信號，如圖4所示。

圖4 星間鏈路信號發射與接收時間段示意

以起始時刻選為0時刻為例，則地面測試設備的星間鏈路距離動態信號的發射時刻{t1,t2,t3,…,tN}為{0,t0,2t0,…,tN}，對應時刻仿真產生的星間距離分別為{d1,d2,d3,…,dN}，最終對應{t1,t2,t3,…,tN}時刻的星間鏈路發射信號分別在{0+d1/c,t0+d2/c,2t0+d3/c,…,tN+dN/c}時刻發出。衛星在每個t0時隙的11/12t0處進行測距，所以測距時刻{t1′,t2′,t3′,…,tN′}實際為{11/12t0,(t0+11/12t0),(2t0+11/12t0),…,tN′}，如圖5所示。

圖5 起始時刻為0時星間鏈路信號發射與接收時間段示意

在進行測距值隨機誤差計算時，被扣減的仿真測距值應選取{11/12t0,(t0+11/12t0),(2t0+11/12t0),…,tN′}時刻對應的實時仿真測距值。

在衛星研制過程中，采用本文方法對星間鏈路接收機測距隨機誤差進行測試，均取得了良好效果。地面測試設備仿真2顆衛星實時星間距離，并發射星間鏈路距離動態信號，星間鏈路接收機獲得的實時測距值(以傳輸延遲時間代表距離值，星間距離等于傳輸延遲時間和光速的乘積，下同)見圖6。地面測試設備仿真產生的模擬距離理論值見圖7。實時測距值減去仿真實時距離值后，測距值曲線見圖8。圖9為實時測距值減去仿真實時距離值后的局部2 h圖。

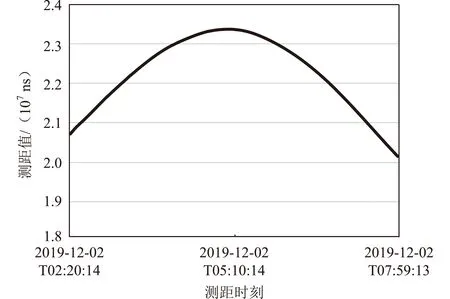
圖6 星間鏈路接收機獲得的實時測距值

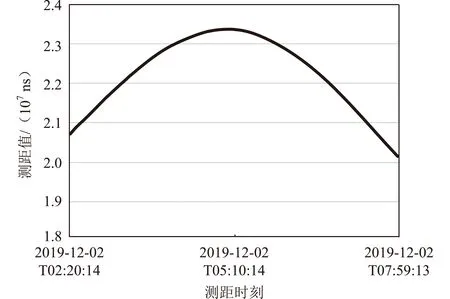
圖7 地面測試設備仿真產生的模擬距離理論值

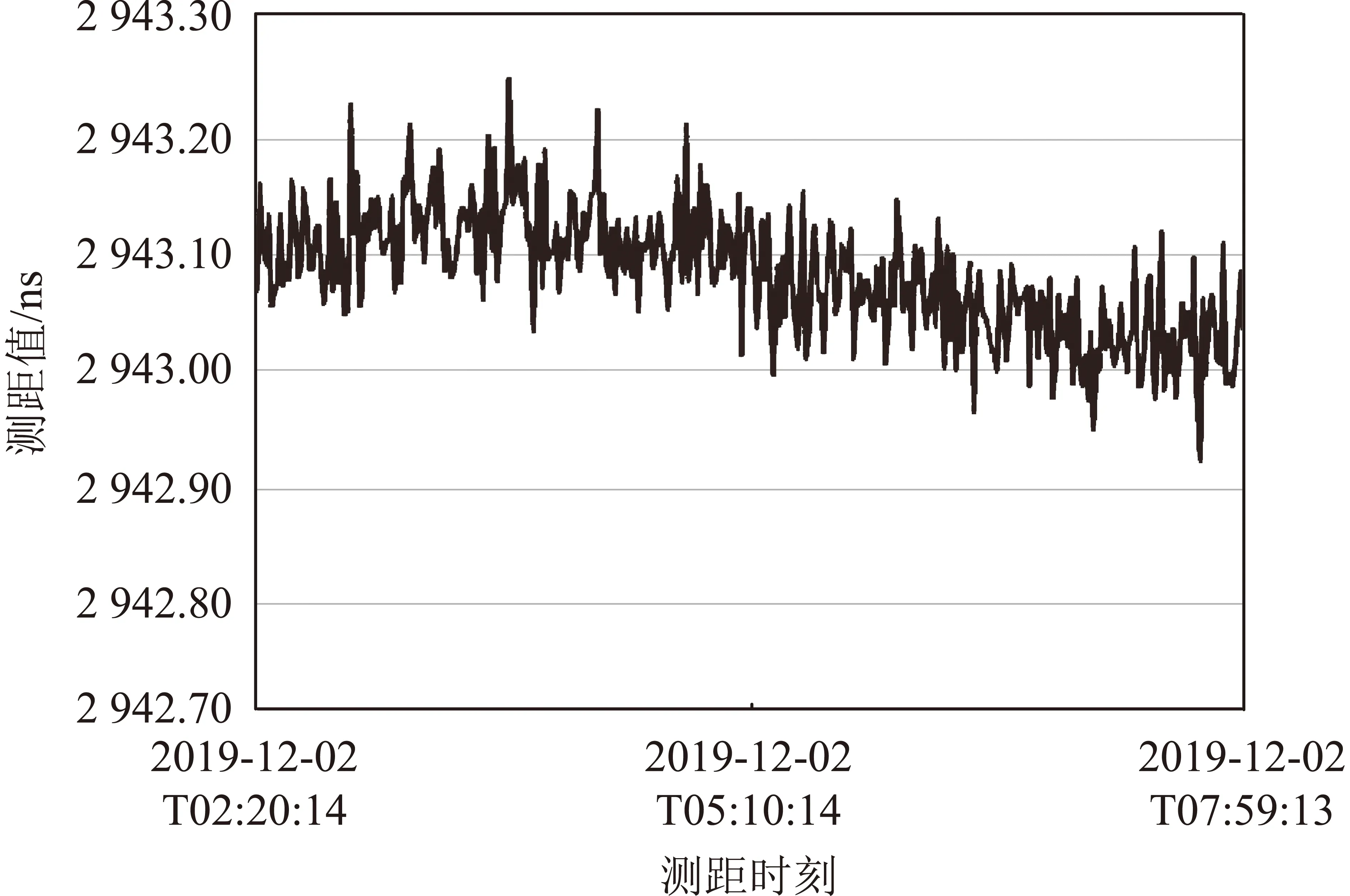
圖8 扣減仿真測距值之后的測距值

圖9 扣減仿真測距值之后的測距值(局部2 h圖)

從圖8可以看出：實時測距值減去仿真實時距離值后，均值穩定，即按照式(3)可以進行隨機誤差計算，本次試驗算得測距隨機誤差值為0.09 ns(即距離值為(0.09×10-6)s×(3×108)m/s=0.027 m)。實際衛星在軌運行過程中，測距隨機誤差平均約為0.5 m，本文方法應用于工程驗證中精度可穩定于厘米級，優于實際在軌運行狀態，能準確地評估軌道動態條件下衛星測距功能準確度。由于實際在軌時大氣阻力、地球引力等變化導致衛星軌道有波動，使用軌道六根數計算相對位置時會產生微小誤差，因此在軌實測數據與本文提出的測試數據相比偏大。隨著衛星性能的持續發展，測試技術提升也需要同步進行，后續可在動態測距及誤差分析方面對測距精度進行進一步的研究和提高。

5 結束語

本文針對距離動態情況下的星間鏈路測距隨機誤差測試問題進行研究，提出了基于軌道動態模型的星間鏈路測距隨機誤差測試方法。該方法的主要思想為：用星間鏈路實時測距值減去對應時刻地面仿真實時距離值，獲得測距觀測殘差，然后對該序列取標準差估計，從而實現測距隨機誤差測試。對星間鏈路實測測距值采用此方法進行驗證，測距隨機誤差低至0.027 m，與星間鏈路實測數據吻合較好，與傳統三角波動態模擬場景等相比，得到了軌道動態條件下星間測距隨機誤差更真實的測試結果。