有效設計初中數學作業的策略探索與實踐
?浙江省杭州市蕭山區新街初級中學 謝涓涓
1 數學教師作業設計的現實問題
長期以來,當要進行作業設計的評比時,很多老師總是參考各類資料、試題等進行編寫,但對作業設計存在一些認識上的誤區:
(1)注重作業題的設計,但很少“借用”已有的優秀作品.如,作業本、課后作業題等,這些作業設計要比一般老師設計得優秀,在“借用”時需要進行合理的取舍與調整.
(2)注意作業的分層布置,但缺少分層體量的控制.如,有的老師設計的是基礎作業10分鐘(5題三層次),選做作業15分鐘(4題,其中有2題可以放到基礎B組中),這樣的設計明顯不夠合理.
(3)注重作業題型的變化,但沒有提高學生興趣的意識.
(4)注意作業設計的新意,如,與生活等知識聯系、讓學生探究等,但缺少對課堂教學切合度的闡述.
…………
作業設計,應該是教師備課的重要一環.好的作業設計,不僅可以鞏固一堂課所要求掌握的知識,而且可以激發學習興趣,開發智力,拓展知識面,點燃思維的火花,培養獨立分析問題和解決問題的能力[1].那么,作業的設計應該怎樣才是合理的,才是最優化的?
2 對作業設計的理解
數學作業設計,指的是教師對所任教的數學學科的作業進行精選、設計、布置,它可以從某個側面反映一個教師的教學設計(預設)與教學控制能力[2].
一般來說,作業設計可從以下的角度進行思考.
2.1 作業內容設計的主要載體與策略
(1)精選現行教材和作業本——也就是結合教師個人的理解,在把握教材的基礎上,選擇教材或作業本中的作業題.
(2)優秀的作業設計——優秀的作業設計都是有其依據和可行性的,可先進行學習和探討,然后再模仿設計相關的數學作業.
(3)學生作業的情況反饋——有效收集學生作業中產生的錯誤,教師結合自己的教學經驗,并分析其中的原因,設計具有針對性的作業.
2.2 作業設計的方向定位
(1)充分尊重并利用教材(作業本)中的典型作業,挖掘深意,用好用足.
(2)通過拓展作業的知識范圍,設計綜合性作業,將目標著眼于培養學生綜合運用知識解決實際問題的能力,提高學生的應用意識.
(3)作業形式注重多樣性、層次性.根據課堂教學的知識結構和學情,提供不同的作業內容,供不同層次學生選擇.
3 有效設計初中數學作業的探索
一方面,我們認為現有作業本、課后作業等是基于更多層面學生的一個普適性作業,需要結合教學實際進行整合與增減;另一方面,在理論學習與教學經驗相結合的基礎上,我們認為初中數學作業的設計應是多角度、多形式、多題型,讓學生多種感官參與活動,使基礎知識、基本技能和應用能力都能得到有效訓練.筆者從添加與補充作業的角度進行研究,給出了自己的設計方法與思考.
3.1基于教材內容理解的作業設計
3.1.1 交流展示型作業的設計
“中位數與眾數”一節的內容比較簡單,筆者布置了自學教材范例,讓學生收集一些相關的數據,并要在課上交流展示的作業.在經歷了小組合作、班級展示、他組補充、學生互評的過程后,很多學生都覺得比以往的課堂效果要好.
設計意圖:不在于解決多少的數學知識或教材中的內容,其關鍵是在于讓學生交流.在給學生充足的時間與空間進行交流后,學生的收獲是讓人欣喜的.
3.1.2 解釋難點型作業的設計
“函數”的概念中,“若對于x的每一個值,y都有唯一的值與之對應”是其中的難點,許多學生通常因為不理解這句話而掌握不了函數的概念.設計如下作業:如圖1,下列表示y是x的函數的圖象是( ).
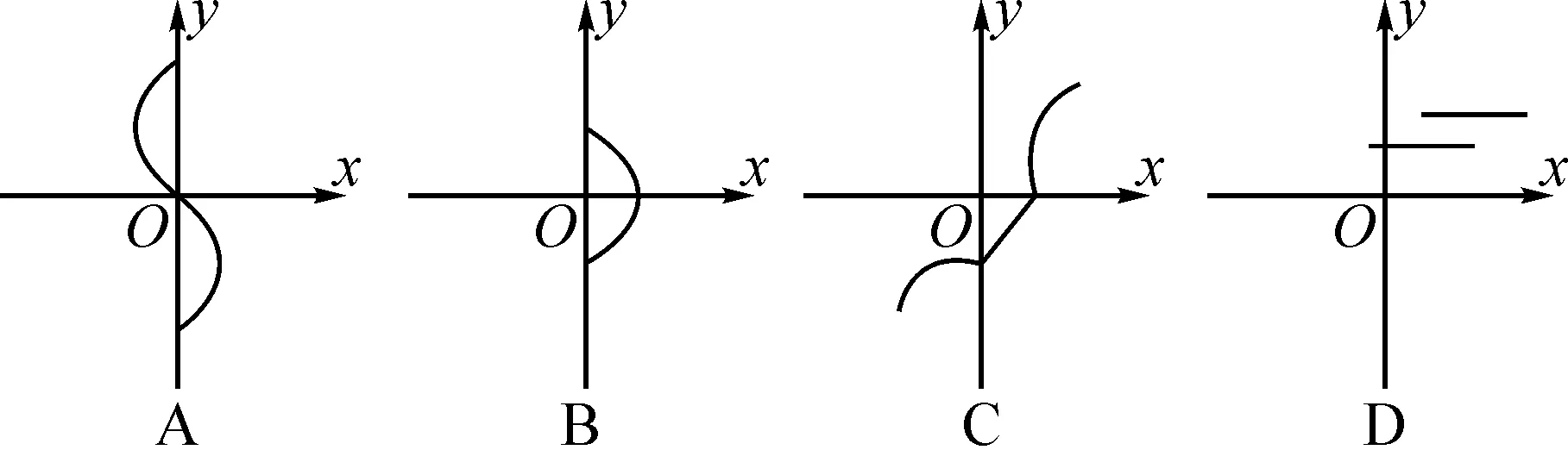
圖1
設計意圖:此作業要求學生詳細閱讀教材,找出最為關鍵的語句,學生才能對函數的概念(x任意,y唯一)有更為清晰的認識.
3.1.3 引導例題型作業的設計

圖2
“一次函數的簡單應用(1)”中的例1(如圖2,題目略),對學生來說,如果沒有經過仔細的閱讀,要解決或完整理解本題的意圖有很大的困難,本例既是教學的重點,又是難點.可設計重點指導學生閱讀的提問式作業:
①本題的數學模型是否能用一次函數來刻畫?
②本題是否就只有一個解?教材中為什么選擇這兩組數據?
③“在直角坐標系中畫出以表中x的值為橫坐標,y的值為縱坐標的7個點”和“過7個點幾乎在同一條直線上所求的函數可以看成一次函數,即可用一次函數來刻畫這兩個量x和y的關系”,這兩句話如何理解?
設計意圖:通過以上的三個問題,幫助學生更好地理解本題的三個要點——①如何刻畫一次函數模型;②多組數據的選擇(7選2)如何選才更合理?③要根據對數據的分析,從簡單與準確兩個維度確立數組的選擇.
3.1.4 拓展內容型作業的設計
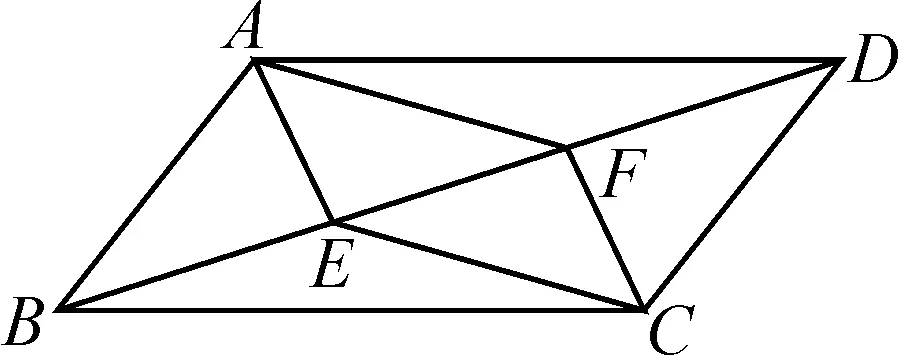
圖3
“平行四邊形的判定(2)”中可設計拓展作業:
請仔細分析和思考本節內容中的例2,已知:如圖3,在平行四邊形ABCD中,E,F是對角線BD上的兩點,且∠BAE=∠DCF.求證:四邊形AECF是平行四邊形.請給出一種與課本不同的證明方法.
設計意圖:尋求與教材例題不同的解答方法,也是對有許多圖形與幾何內容的課時作業的一種設計思路,其目的是促進學生掌握知識.
3.2 基于課堂內容梳理的作業設計
3.2.1 舊知識與新知識的類比梳理作業設計
在“不等式的基本性質”學習后,設計作業:如表1,比較等式與不等式的基本性質.
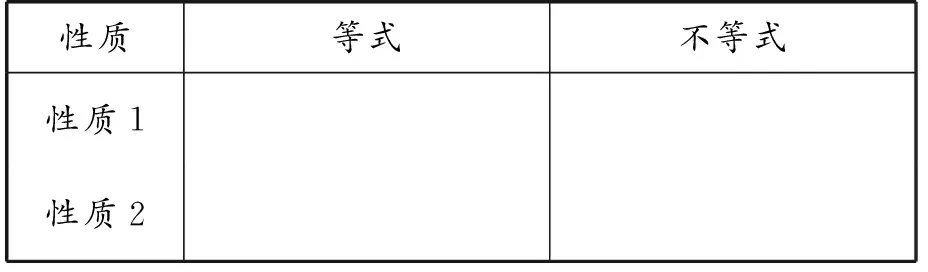
表1 等式與不等式性質比較
設計意圖:初中數學知識是螺旋上升的,前面學過的知識對后面的知識有很大的促進作用,教師可以采用類比的方式促進學生掌握知識.
3.2.2 進行新知識梳理的作業設計
“一元一次不等式組”課后設計作業:一般由兩個一元一次不等式組成的不等式組有四種基本類型,它們的解集、圖示、口訣表示如表2,請完成表格.

表2 一元一次不等式組解的表示及口訣
注:表2中a 設計意圖:利用表格(或圖示)的方式進行知識的梳理是教師在課堂上經常采用的方式,對于學生而言,若不是自己梳理,學習所得還是不夠的. 3.2.3 對知識或題技巧進行梳理的作業設計 (1)“代數式”中設計作業:列代數式時有哪些需要注意的點? (2)“頻數分布直方圖”中設計作業: ①繪制頻數分布直方圖時應注意什么?②頻數分布直方圖比頻數分布表更具有那些優勢? (3)“三角形的中位線”中設計作業:在利用三角形的中位線解題時往往需要添加輔助線,應如何添加輔助線?又有哪些注意之處? 設計意圖:結合課堂教學的具體內容,對教材的知識進行梳理,更有助于學生系統地掌握相關的知識結構或體系. 3.3.1 加入學生自己理解的作業設計 八年級上冊“3.1認識不等式”的作業中加入這樣的題目: 圖4 星期天,802班有27名學生去公園游玩,班長準備好了零錢到售票處買27張票時,被小君同學喊住了,提議買30張票,如圖4. (1)有人說多買不是浪費嗎?那么小君同學的提議究竟對不對? (2)最多可以有多少同學一起去該公園,多買票是劃算的? 設計意圖:以上這樣的作業設計,通常在學生理解知識的基礎上完成,而且答案適當帶一點開放性,每個學生的解答應該不完全相同,這樣則更有助于學生掌握知識和深入學習. 3.3.2 基于學生思維問題的作業設計 學了“等腰三角形性質”后設計作業: 圖5 如圖5,△ABC是等腰三角形:AB=AC,倘若不小心,它的一部分被墨水涂染.想一想,有什么辦法把原來的等腰△ABC重新畫出來? 設計意圖:學生一見題后,興趣就來了,想出了一種方法后,興趣不減,繼續思考.最后在作業本上出現了三種方法——①作∠B=∠C;②作BC的中垂線;③對折. 3.3.3 促進學生深入探究的作業設計 圖6 “平行線的判定方法”一節中,充分利用課本的探究活動設計作業:有一條紙帶,如圖6,如果工具只有圓規,怎樣檢驗紙帶的兩邊是否平行?(學生解答) 解答1:如圖7,折出折痕(用直尺劃線),用“畫一個角等于已知角”的方法比較∠1與∠2的大小. 圖7 圖8 圖9 解答2:如圖8,折出兩條垂直于一邊的折痕AC,BD,用“畫一條線段等于已知線段”的方法比較AC和BD的大小. 解答3:如圖9,在一邊上取一點A,使AC=AB,再以點C為圓心,AC長為半徑畫弧,交另一邊于點D,比較AC和BD的大小. 設計意圖:適度改變幾何枯燥乏味的面孔,學生對此表現出了濃厚的興趣,爭相給出方法.初中生對新奇事物比較敏感,有興趣,因為傳統的數學問題形式往往沒有親切感.探究活動可能無法在新課教學過程中完成,可以補充在練習課中.由于探究活動在教材中所占比例較大,對提升學生的學習興趣起到持續的作用,應成為我們平時教學中一塊重要的陣地. 探究性作業的設計一般在新授課后,采用課外小組活動,讓學生通過觀察、調查、假設、實驗等多種形式的探究活動,提出自己的解釋,或者設計和制作自己的作品.這種作業設計的基本流程是:提出問題—深化教材—查找資料—動手操作—成果匯報—總結評價.這種知識性的探究作業,既克服了以往作業的缺點,又提高了學生分析問題的能力[3]. 經過不斷地探索與實踐,筆者收獲頗豐.通過深入挖掘教材內涵,在立足教學目標的同時創造性地設計更為合理的初中數學作業,從而讓我們的課堂變得更加精彩,學生更加喜歡,作業設計也更有效、更豐富. 但是,筆者也深刻地感受到:在初中數學教學中,作業的“質”與“量”還沒調節到最佳狀態,還有很多有待進一步深入思考的話題: (1)如何在設計作業時,找出教學內容與學生生活經驗之間的最佳結合點?選擇的作業類型要緊扣語言點,如何促進學生語言交際能力的發展? (2)如何改進現有的對學生學習的評價方式,進而確保作業的有效和高效實施? (3)作業賴以生存的環境應該是學生的生活實際,離開學生生活實際的作業,會成為無本之木.學生對這樣遠離自己生活實際的作業只會敬而遠之,甚至會產生抗拒的心理.如此,原本基于學生發展為初衷的作業就不自覺地成為了學生健康成長的絆腳石.3.3 基于學生數學認知的作業設計




4 結束語

