化歸思想在初中數學解題中的運用
?江蘇省無錫市鳳翔實驗學校 馬 琦
1 引言
當前初中生在數學學習過程中存在著這樣的現象:他們關注更多的是這道題做對了沒有;如果錯了,是在哪一步出錯.他們沒有在宏觀上去關注這道題,即這道題體現的數學思想是什么,用這樣的思想還能解答哪些類似的題目.其實當學生從數學思想的角度去探究問題時,會在“山重水復”中窺見“柳暗花明”.因此,在教學中教師要培養學生關注數學思想的意識,比如培養學生化歸思想,以提升他們的學習能力.運用化歸思想解決數學問題,就是在研究和解決有關數學問題時,教師要指導學生先思考采用什么樣的手段將問題進行轉化,而不是具體的解題步驟.
2 由陌生引向熟悉,體會化歸思想
教師要培養學生的讀題能力,即學生解題時,先要讓他們以自己的方式解讀這道題.學生在讀題的時候,要能讀出這道題中有哪些是熟悉的,有哪些是不熟悉的認知、問題.當學生大致認清題目的面目之后,教師就可以引導他們將陌生的問題轉化為熟悉的問題,在運用中體現化歸思想.
以蘇科版九年級上冊“直線與圓的位置關系”這一章節為例,教師設置這樣的題目:如圖1所示,AB是⊙O的弦,點C在過點B的切線上,OC⊥OA,OC交AB于點P.若∠BPC=70°,則∠ABC的度數等于多少?
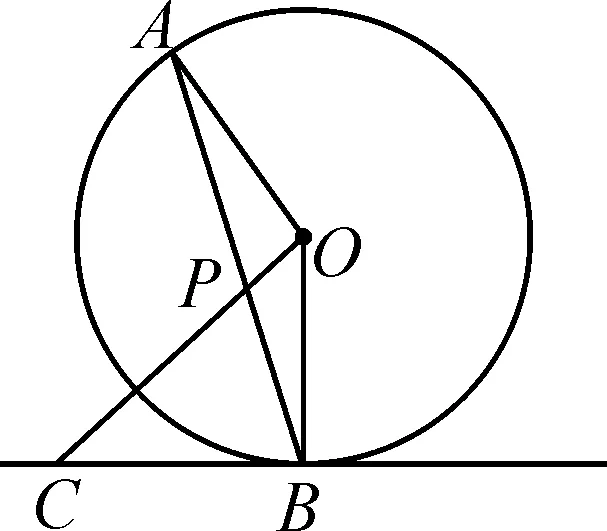
圖1
學生發現題目中的條件都是一些常見的條件,無非就是某條直線與某個線段垂直,某個角等于多少度,但是發現要求的這個角度是陌生的,這個陌生體現在它幾乎與題面上任何角都沒有關系.教師要指導學生進行角度之間的轉化,讓化歸思想體現出來.學生先是從∠ABC這個陌生的角入手,將其轉化為“∠OBC-∠OBA”.這其中∠OBC的度數可以從“點C在過點B的切線上”這一條件獲得,即∠OBC為90°;也就是說,學生將完全陌生的角轉為一個熟悉的角與另一個陌生的角的差,接著繼續將∠OBA進行轉化.根據題目圖形,學生不難得出“∠OBA=∠A”這一結論,但∠A也是一個陌生的角.再次轉化,發現在∠A所在的三角形中,因為OC⊥OA,所以∠AOC=90°,所以可將∠A轉化為“90°-∠APO”.而∠APO也是一個陌生的角,題目中沒有提及,但是題目中提到的是它的對頂角∠BPC等于70°,進而學生再次轉化,得出∠APO等于70°.很顯然,在這個題目中學生秉持的理念就是要將不熟悉的角度進行轉化,只是這個轉化不是一步到位,需要經過多次轉化,最后變成學生熟悉的問題情境.因此,在教學中,教師可指導學生將問題分為熟悉的與不熟悉的兩大類,再在中間不斷地轉化,進而達到化解問題的目的.
3 由特殊引向一般,了解化歸思想
學生解題時會遇到具體的問題情境,即要求學生運用所學的知識解決實際生活中的問題.對于這樣的題目學生可以運用化歸思想進行層層轉化,將特殊的問題轉化為一般性的問題,進而為問題的解決提供便利[1].
以蘇科版數學八年級上冊“勾股定理”為例,教師將這樣一道題展示給學生:今有竹高一丈,末折抵地,去本三尺,問折者高幾何?這是《九章算術》里的一道題,教師想讓學生在運用化歸思想的同時,感知中國古人的智慧.學生將這段文言文轉化為白話文:一根竹子原高1丈,中部有一處折斷,竹梢觸地面處離竹根3尺,試問折斷處離地面多高?教師首先要求學生將題目的文字內容轉化為圖形,并按照題目的要求將相關的數據標出來,然后引導學生將題目中“竹子”這一特殊的情境換掉,變成一個一般性的圖形.換言之,教師指導學生進行特殊性到一般性的轉化.
學生將原題中的已知條件轉化成圖2,對照這個圖形,首先假設A,B之間的距離為x尺,依據題意可知A,C之間的距離就為(10-x)尺,因為題目中BC的距離是3尺,依據勾股定理,列出x2+32=(10-x)2.從整個過程來看,教師主要指導學生從特殊的情境中看到一般性的問題.學生要能將原題目的一些特殊性的表述轉為一般的數學化的敘述,進而促成問題的解決.教師指導學生由特殊性到一般性轉化的過程就是展示化歸思想的過程.
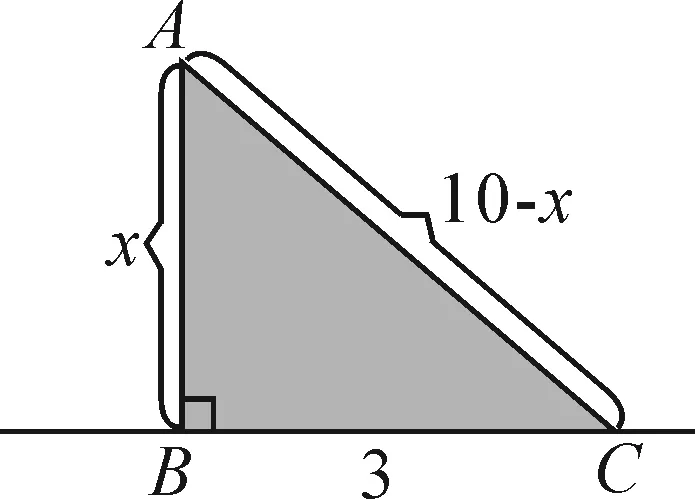
圖2
4 由復雜引向簡單,應用化歸思想
學生在學習數學的過程中遇到的常見的困難就是不會將復雜的問題轉化為簡單的問題.化歸是重要的數學思想,最主要的就是在不停的轉化中將問題解決.將復雜轉為簡單就是化歸思想的主要展現形式.由復雜往簡單轉化,主要是將復雜的問題簡化,當然也包括將復雜的表述簡化.
以蘇科版數學七年級上冊“一元一次方程的應用”為例,教師設置這樣的題目:某公司會計欲查詢乙商品的進價,發現進貨單已被墨水污染,如表1.
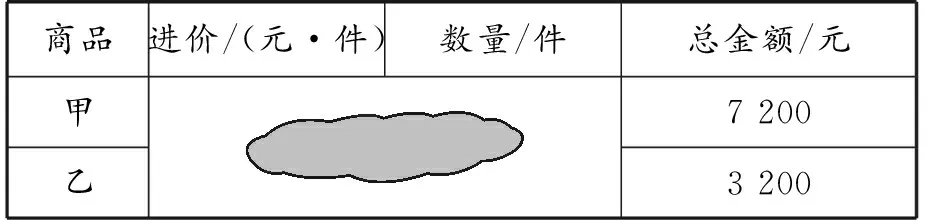
表1 進貨單
商品采購員A和倉庫保管員B對采購情況回憶如下:
A:甲商品進價比乙商品進價每件高50%.
B:甲商品比乙商品的數量多40件.
請你求出乙商品的進價,并幫助他們補全進貨單.
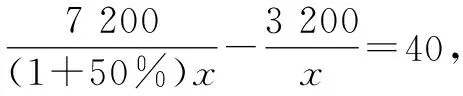
5 結束語
化歸不僅是一種重要的解題思想,也是學生在學習數學的過程中應具有的最基本的思維策略,當然也是一種有效的數學思維方式.學生學習數學的過程就是不斷改變思維策略、提升思維品質的過程.換言之,在教學過程中,教師要關注學生的思維發展,進而促進他們素養的生成.教師重視化歸思想在解題中的運用,其實也就是重視學生思維能力的培養,只是將思維的培養進一步上升到宏觀的高度,居高處臨下,于高屋處建瓴[2].

