例析“角平分線”在思路探究中的作用
?甘肅省武威市天祝藏族自治縣新華中學 趙 霞
1 引言
經歷了幾何解題思路探究的過程后,人們通常會發現到找出解題的突破口非常關鍵[1].基于此,本文中借助幾道例題分析“角平分線”對初中幾何解題思路探究發揮的作用,希望對一線教師有所啟發.
2 例題引入,思路探究
例1如圖1,已知在Rt△ABC中,∠ACB=90°,∠B=60°,AD平分∠BAC,CE平分∠BCA,AD與CE相交于點F,FM⊥AB,FN⊥BC,垂足分別為點M,N.求證:FE=FD.
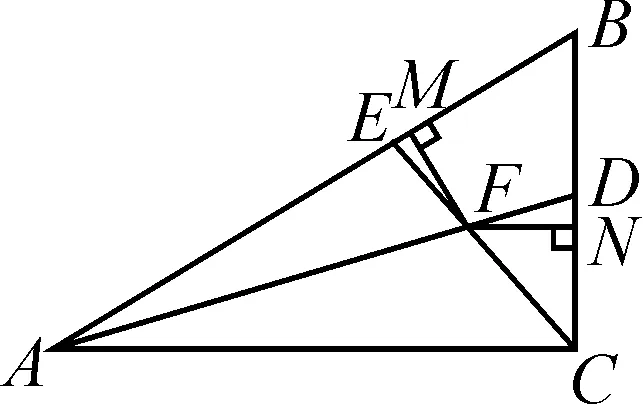
圖1
分析:本題可根據題目已知條件及角平分線定理作出點F到AC的距離,如圖2所示.然后,通過FN的“橋梁”作用證明FM=FN.最后,在證明△FME和△FND全等的基礎上得到FE=FD.
證明:如圖2所示,過點F作AC的垂線,垂足為H.
∵AD平分∠BAC,CE平分∠BCA,且FM⊥AB,FN⊥BC,
∴MF=FH=NF.
∵∠ACB=90°,∠B=60°,
∴∠MEF=75°,∠FDN=75°.
∴△FME≌△FND(AAS).
∴FE=FD.
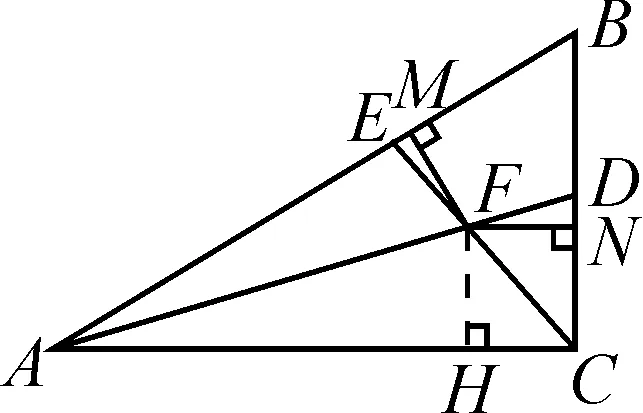
圖2
例2已知:如圖3所示,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分線.求證:BD=2CD.
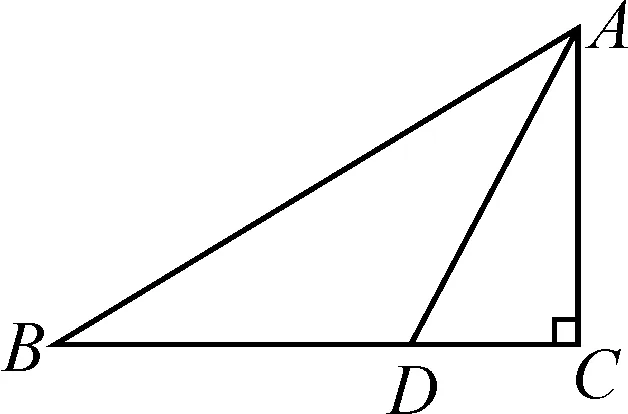
圖3
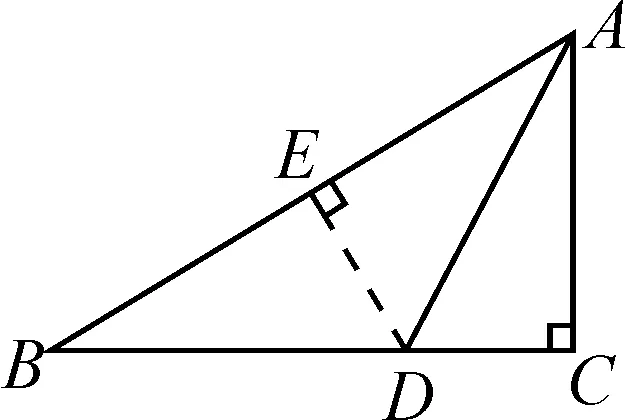
圖4
分析:本題條件不多,對尋找解題突破口最有幫助的是“AD是∠BAC的角平分線”這個條件.這類題和角平分線的性質有關,常結合等腰三角形、垂直平分線、直角三角形30°角的性質定理等知識,相對比較基礎.
證明一:∵∠C=90°,∠B=30°,
∴∠BAC=60°.
∵AD是∠BAC的角平分線,
∴∠BAD=∠CAD=30°.
∴BD=AD,AD=2CD.
∴BD=2CD.
證明二:如圖4,過點D作AB的垂線,垂足為點E.
∵AD是∠BAC的角平分線,
∴CD=ED,∠BAD=∠CAD.
∵∠C=90°,∠B=30°,
∴∠BAC=60°.
∴∠BAD=30°.
∴AD=2ED.
∵∠B=∠BAD=30°,
∴BD=2ED.
∴BD=2CD.
例3已知:如圖5所示,△ABC的外角∠CBD和∠BCE的角平分線分別是BF,CF,且這兩條角平分線相交于點F.求證:點F在∠DAE的角平分線上.
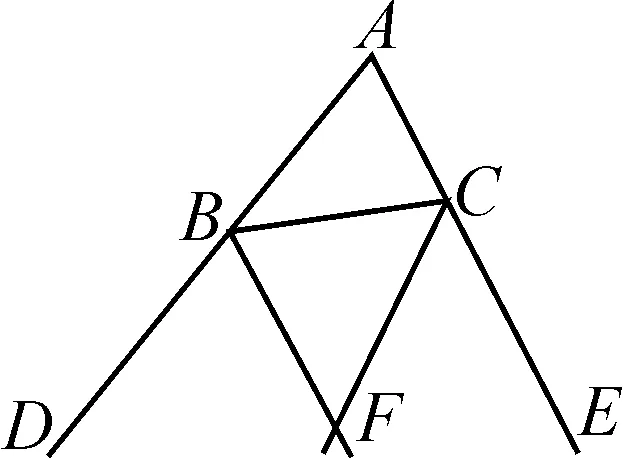
圖5
分析:本題給出的條件非常少,但當已知角平分線時,不妨將角平分線上的點到角的兩邊的垂線段作出來,然后結合“角平分線的判定定理”證明“點F在∠DAE的平分線上”.但是,要注意說明點F在∠DAE的內部,這是角平分線判定定理使用的前提.由此可見,抓住“角平分線”這個關鍵條件并借助它的性質解決問題非常重要.
證明:如圖6所示,過點F分別作AD,BC,AE的垂線,垂足分別為點G,H,M,連接AF.
∵BF和FC分別是△ABC的外角∠CBD和∠BCE的角平分線,
∴GF=HF=MF.
∵點F在∠DAE的內部,
∴點F在∠DAE的角平分線上.
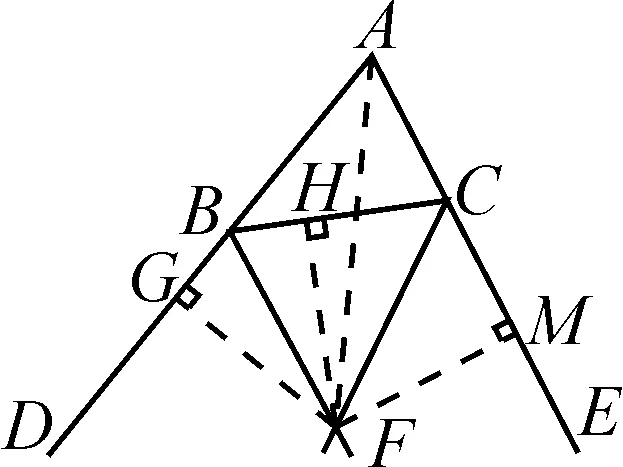
圖6
3 總結經驗,發揮作用
通過以上三道例題的分析不難發現,“角平分線”這個條件一旦題中給出,那么常會對解題發揮如下作用.
首先,引導思路.“角平分線”的出現讓學生的解題思路不知不覺傾向于與之有關的性質定理和判定定理,而這些都與“點到角的兩邊的距離相等”有關[2].所以,這就提醒學生需要作出與“點到角的兩邊的距離”有關的輔助線.但是,這里的輔助線通常有兩種情況:第一,題中已經給出了“點到角的一邊的距離”,需要再作出與“點到角的另一邊的距離”有關的垂線段,如例1、例2都是如此;第二,題中只已知角平分線,但這個點到角任何一邊的距離是未知的,此時需要將點到角的兩邊的垂線段都作出,如例3便是如此.
其次,變中有定,訓練思維.題中作輔助線的方式雖然有差異,但是證明過程具有相同點,即發揮等量代換的作用實現三角形全等的證明.這主要表現在以下兩個方面(以上述題目為例):第一,都利用了“等量代換”.如例1中通過“FM=FH,FH=FN”中的FN起到“橋梁”作用,證明了FM=FN;如例2中可將“BD=2DE”的“DE”根據“DE=CD”代換,最終得到“BD=2CD”;再如例3中通過“FG=FH,FH=FM”證明了FG=FM.第二,都可用“全等三角形”證明.由此可見,“角平分線”和“全等三角形”具有非常密切的聯系[3].
最后,構建知識網絡.角平分線和垂直平分線在初中幾何題中同時出現的可能性非常大,而這“兩線”無論是定義、性質、判定,還是尺規作圖的方法都非常相似,學生在學習時極易混淆.但是,角平分線的出現,常讓學生聯想到垂直平分線,從而將二者聯系起來,從而構建更豐富、完善的知識網絡體系[4].例如,學生在題中接觸了角平分線后,由角平分線的性質、判定聯想到垂直平分線的性質、判定,或者聯想到它們的尺規作圖方法,從而衍生出類似的思維導圖.一旦這樣的思維導圖建立,那么學生就能從一個“點”出發聯想到更多的“點”,而點與點之間往往可構成知識網絡.所以,作為初中數學教師有必要在角平分線出現的同時,將之與垂直平分線聯系起來,從而給予學生更多構建知識網絡的機會,讓他們更靈活地掌握和運用知識.
4 結語
總之,若題中給出了“角平分線”這個條件,那么它將對這道題解題思路的探究發揮積極的作用.學生要在熟練掌握角平分線性質定理和判定定理的基礎上,靈活作出點到角平分線的距離的輔助線,以此找到解決問題的突破口.

