碳纖維角聯織機經紗張力的H∞網絡化控制
夏鵬飛, 劉薇,2*
(1.天津工業大學機械工程學院, 天津 300380; 2.天津工業大學天津市現代機電裝備技術重點實驗室, 天津 300387)
碳纖維作為一種基礎性原材料被廣泛應用于航空航天、新能源汽車等高尖端領域[1],碳纖維角聯織機的關鍵控制技術研究對于碳纖維織物的性能提升具有重要意義[2]。碳纖維角聯織機是一種含有多子系統分散協同工作的復雜裝備,其控制系統為分布式、網絡化的在整個控制期間,信號是通過CANbus網絡傳輸的.整個張力控制系統的穩定性會不可避免受到時延、數據丟包等網絡特性干擾。
關于織機張力系統的控制問題,文獻[3]針對多電機卷繞系統中存在的多因素非線性耦合、外部擾動、內部參數不確定性,提出了一種分散H∞魯棒控制器,仿真結果表明:所提出的控制器可較好地抑制外部擾動和卷取子系統間耦合作用產生的張力波動,大大提高了卷繞系統的張力控制性能。文獻[4]針對雙輥卷繞張力系統設計了一種混合擺動輥,并采用比例、積分(proportional integral,PI)控制器控制驅動輥的運轉速度,實現了張力系統的穩定。文獻[5]分析了織機卷取機構的力學模型,利用神經網絡比例、積分和微分(proportional integral derivative,PID)控制器實現了卷取機構的恒張力控制,具有較高的控制精度。然而,現有的研究在進行張力控制器的設計時往往忽略了網絡因素對其穩定性產生的影響。
近年來,中外學者對網絡化控制系統開展了大量理論研究,并取得了一定的成果[6]。文獻[7]針對離散網絡化控制系統中由于數據包丟失、網絡時延而導致的系統控制穩定性能變差的問題,設計了一種切換狀態反饋控制器,并通過仿真表明所設計的控制器是有效的。文獻[8]針對一類具有執行器和傳感器故障的網絡控制系統,提出了一種基于系統估計信息的快速高階滑模控制器,驗證了其對系統故障和外部擾動的魯棒性。網絡化控制系統也被廣泛應用于許多領域,文獻[9]提出了一種基于觀測器的無人艇航向控制器,實現了網絡環境下無人水面艇的航向精確控制。為了抑制分布式網絡化電力系統中存在的低頻振蕩現象,文獻[10]提出了一種T-S(Tkagi-Sugneo)模糊網絡化控制策略,實現了系統的穩定性;文獻[11]提出了一種H∞輸出反饋耦合控制策略,實現了車與車相耦合的智能車網絡化控制系統的穩定控制。然而現有的文獻鮮有涉及紡織工業中網絡化控制系統的研究。
因此,研究將先進的網絡化控制理論應用于碳纖維角聯織機的經紗張力控制,解決網絡干擾等不確定因素給張力控制系統帶來的消極影響,對網絡化控制系統在紡織工業的實際應用有著重要意義。為此,首先給出帶有非線性開口系統擾動的三自由度碳纖維角聯織機系統狀態方程,并將網絡化控制思想應用于織機的張力控制上,在織機數學模型中引入時延、丟包等網絡因素的影響,建立其網絡化控制模型。然后,在該網絡化控制模型的基礎上,提出一種基于觀測器的網絡化最優H∞控制器,最終通過仿真實驗驗證該控制策略對經紗張力的控制效果。
1 碳纖維角聯織機系統模型建立
碳纖維角聯織機織造原理如圖1所示,在織造過程中,經紗受開口、卷取、送經、引緯和打緯機構共同作用而產生形變,導致經紗張力在同一時間內受多個機構共同作用,其變化是一個復雜過程。
1.1 碳纖維經紗力學模型建立
碳纖維是一種黏彈性材料,其力學性能兼具彈性固體與粘性流體特征,表現在具有蠕變和應力松弛現象。實際工作中碳纖維紗線被要求恒張力拉緊,其松弛現象很微弱,因此盡管實際工作中碳纖維紗線不是理想的Kelvin模型,但卻可以滿足建模精度,為簡化其動力學特性的分析,對碳纖維紗線的動力學分析中采用Kelvin模型。
Kelvin模型是由胡克彈簧和牛頓黏壺并聯組成的,其結構如圖2所示。Kelvin本構方程為
(1)
式(1)中:E為彈簧的彈性模量;η為黏壺的粘性系數;σ(t)為模型受到的應力;ε為形變;t為時間。
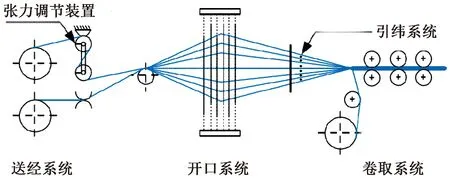
圖1 碳纖維角聯織機織造原理圖Fig.1 Weaving principle diagram of carbon fiber diagonal loom

圖2 Kelvin模型圖Fig.2 Kelvin model diagram
根據Kelvin模型,可得經紗張力表達式為
(2)

1.2 碳纖維角聯織機系統動力學分析
送經系統的結構簡圖如圖3所示,送經系統4個區域內張力T1、T2、T3、T4之間的關系可表示為
(3)

MT1、Ms1分別為電機的電磁轉矩和轉軸的摩擦轉矩圖3 送經系統結構示意圖Fig.3 Structure diagram of let-off system
式(3)中:Jz1、Jz2、Jz3分別為回轉輥、擺動輥、支撐輪的轉動慣量;Rz1、Rz2、Rz3分別為回轉輥、擺動輥、支撐輪的半徑;Cz1、Cz2、Cz3分別為回轉輥、擺動輥、支撐輪的黏性摩擦系數;ωz1、ωz2、ωz3分別為回轉輥、擺動輥、支撐輪轉動角速度。
送經軸等效半徑的一階微分可表示為
(4)
式(4)中:h為經紗厚度。
送經軸的轉動慣量可表示為
(5)
式(5)中:Jm1為送經軸空載轉動慣量;ρ為經紗的質量密度;b為經紗的寬度;r1為送經軸的空載半徑。
根據送經軸和卷取輥的轉動慣量和角動量之間關系,可得

T1(t)R1(t)
(6)
式(6)中:MD1為送經電機的電磁轉矩;i1為送經電機的減速比;CS1為送經軸的黏性摩擦系數。
卷取系統的結構簡圖如圖4所示,卷取系統兩個區域內的經紗張力T5、T6的關系可表示為

(7)
式(7)中:Jz4(t)為卷取系統支撐輪的轉動慣量;Rz4為卷取系統支撐輪半徑;Cz4為卷取系統支撐輪黏性摩擦系數;ωz4(t)為卷取系統支撐輪轉動角速度。
卷取軸等效半徑的一階微分可表示為
(8)
卷取軸的轉動慣量可表示為

圖4 卷取系統結構示意圖Fig.4 Structure diagram of winding system

(9)
式(9)中:Jm2為卷取軸的空載轉動慣量;b為經紗寬度;r2為卷取軸的空載半徑。
根據卷取輥的轉動慣量和角動量之間關系,可得

T5(t)R2(t)
(10)
式(10)中:MD2為卷取電機的電磁轉矩;i2為卷取電機的減速比;CS2為卷曲輥的黏性摩擦系數。
實際工作過程中,影響織機紗線張力的因素很多,為了接下來更方便的研究,假設:各轉輥和支撐輪均為理想質輕材料,摩擦系數非常小,且在織機運行過程中均為勻速運動。

基于假設可得
T1(t)=T2(t)=T3(t)=T4(t)=
T5(t)=T6(t)=T(t)
(11)
式(11)中:T為織機運行過程中的動態經紗張力,它在紗線任一處都是相等的。
聯立式(7)、式(10)、式(11)得
(12)
式(12)中:Kw、Bw分別為經紗的彈性系數和阻尼系數。
進一步引入開口系統產生的經紗張力影響,根據文獻[12]可知,碳纖維角聯織機開口機構造成的經紗長度變化Lk(t)可表示為
Lk(t)=λsin2ζt
(13)
式(13)中:λ為織機梭口相關參數;ζ為碳纖維角聯織主軸轉動速度。

(14)
2 碳纖維角聯織機網絡化控制策略研究
碳纖維角聯織機送經系統分為60套獨立的送經裝置,考慮到實施控制的成本和系統可靠性等因素,不能設置過多傳感器,因此很難直接用狀態反饋控制器進行控制,如果可以設計觀測器估計實際狀態,進而實現狀態反饋,則更適合于實際的織機紗線張力控制。其次由于碳纖維角聯織機運行過程中,系統同時存在不確定的開口系統擾動以及時延和丟包等網絡干擾。H∞控制是把外部考慮在內的一種控制器,既保證了穩定性,又保證了外部擾動下的系統動態性能[13]。因此,將設計一種基于觀測器的最優H∞控制器來實現織機系統在外部擾動和網絡干擾下的恒張力控制。碳纖維角聯織機工作原理圖如圖5所示。
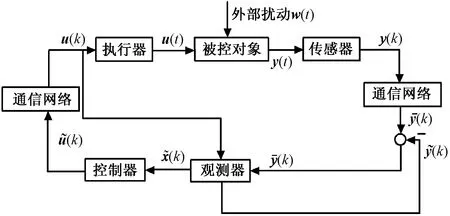
圖5 碳纖維角聯織機控制系統結構圖Fig.5 Control system structure diagram of carbon fiber diagonal loom
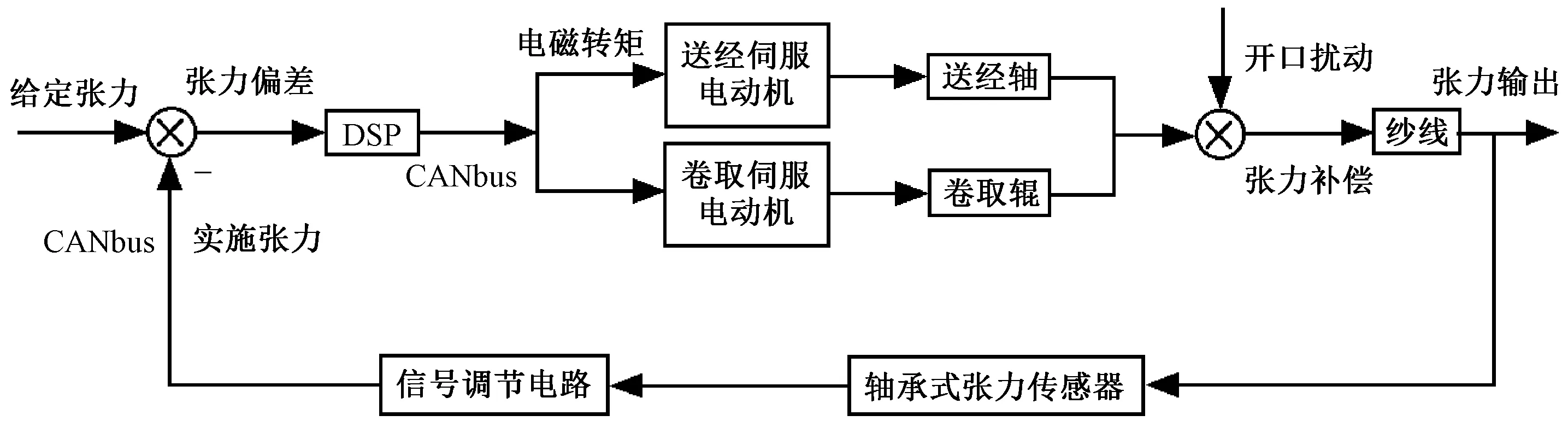
數字信號處理器(digital signal processing,DSP) ;CAN總線(controller area network bus,CANbus)圖6 網絡化控制系統結構示意圖Fig.6 Structure diagram of networked control system
考慮CANbus網絡環境下,織機的網絡化控制系統結構如圖6所示。
2.1 網絡化控制系統模型建立
基于所提出的織機系統數學模型,考慮離散時間網絡化模型為
(15)
式(15)中:x(k)∈Rn為系統狀態;u(k)∈Rm為控制輸入;y(k)∈Rp為測量輸出;z(k)∈Rq為系統輸出;w(k)∈Rr為外部擾動;A1、B1、E1、C1、D、E2、G為適當維數的系數矩陣。
考慮該離散網絡化控制系統具有的觀測器可表示為
(16)
考慮設計的狀態反饋控制器可表示為

(17)
式(17)中:K為狀態反饋控制器的增益矩陣。
進一步將通信網絡中的時變時延和數據丟包現象代入式(19)、式(20)中,可將該時變時延的不確定性轉化為系統系數矩陣的不確定性表示,丟包現象可用兩個獨立的伯努利隨機分布表示[14],從而得到帶有參數不確定性的離散時間系統狀態方程網絡化模型,可表示為

(18)
式(18)中:β(k)為伯努利隨機分布序列,用來描述控制器端到執行器端的丟包現象;dk為控制器到執行器間的網絡傳輸時變時延,且滿足dm 考慮時延丟包現象后的有參數不確定性的離散時間系統的觀測器,可表示為 (19) 式(19)中:α(k)為伯努利隨機分布序列用來描述傳感器端到控制器端的丟包現象;τk為傳感器到控制器間的網絡傳輸時變時延,且滿足τm<τk<τM,其中τm和τM分別為τk的上、下限。 定義狀態觀測誤差為 (20) (21) 針對式(21)所描述的閉環系統,研究系統滿足均方指數穩定及H∞穩定的充分條件。為了進一步的證明,給出如下引理。 (22) 引理2對于給定的具有適當維數的矩陣Q=QT、Γ、Ψ、FFT<0。 Q+ΓFΨ+ΨTFTΓT<0 (23) 則式(23)成立的充要條件是存在一個正數ε>0使得式(24)成立。 Q+ε-1ΓΓT+εΨTΨ<0 (24) (25) 式(25)中:I為單位矩陣;γ為H∞性能指標。 證明:引入Lyapunov二次泛函: (26) 則可得 ΔV(k)=E{V(k+1)|η(k)}-V(k) (27) (28) 則可知當式(29)成立時,ΔVk≤0恒成立。 ηT(k)Λη(k)≤0 (29) 不妨令Λ<0,此時有 E{V(k+1)|η(k)}-V(k)=ηT(k)Λη(k) ≤-λmin(Λ)ηT(k)η(k) (30) 式(30)中:λmin為矩陣的最小特征值。 對于整數k=0,1,…,c,計算式(30)兩側的數學期望之和,可得 (31) 從而可得 (32) J=E[ΔV(k)]+E{zT(k)z(k)|ξ(k)}- γ2wT(k)w(k) =E{zT(k)z(k)|ξ(k)}-γ2wT(k)w(k)+ΔV(k) γ2wT(k)w(k)+ΔV(k) (33) 進一步,根據式(25),并運用引理1,可得 E[ΔV(k)]+E{zT(k)z(k)|ξ(k)}- γ2wT(k)w(k)≤0 (34) 即 (35) 則定理1得證。 由于實際求解不等式[式(25)]過程中,ΔB、ΔC、ΔD等非線性項均存在于增廣后的系統矩陣參數,因此該不等式是不滿足LMI條件的。 PS=I,QR=I (36) 證明:注意式(25)可重新表示為 (37) 由ΔB1、ΔC1、ΔD的結構可知,存在適當維數的常數矩陣H1、H2、M1、M2、M3,和未知的不確定矩陣F(dk)、F(τk)使得 (38) ΔC1=H2F(τk)M3 (39) 式中:F(dk)、F(τk)為未知不確定矩陣,且滿足F(dk)FT(dk)≤I,F(τk)FT(τk)≤I。 將式(31)代入式(30)中可得 (40) 進而根據引理1可證定理2。由于式(36)中等式約束的存在,該矩陣不等式仍為非線性,因此該不等式矩陣仍非線性矩陣不等式(linear matrix inequality,LMI)可解。根據錐補線性化迭代(cone complementary linearisation,CCL)方法[16],采用一如下種凸優化方法來解決該非凸可行性問題,從而獲得最優H∞控制器。算法步驟如下。 步驟1給定一個充分大的初始性能指標γ0,使得不等式存在LMI可行解。 步驟2令k= 0,分別對于矩陣P、Q、S、R、K、L尋找滿足不等式的一組初始可行解并記為{P0、Q0、S0、R0、K0、L0}。 步驟3求解式(41)、式(42)所示的凸優化問題。 Minimize tr{PkS+PSk+QkR+QRk} (41) (42) 將所得出的解記為:{Pk+1、Qk+1、Sk+1、Rk+1、Kk+1、Lk+1}。 步驟4將所得到的解{Pk+1、Qk+1、Kk+1、Lk+1}代入定理2中,若滿足,做如下最優解的賦值運算:{Popt、Qopt、Kopt、Lopt} = {Pk+1、Qk+1、Kk+1、Lk+1},并令γopt=γ-Δγ,其中Δγ為迭代算法中賦予性能指標的一個增量,返回步驟1;如不滿足,且k 碳纖維經紗材料相關參數和碳纖維角聯織機的系統相關參數分別如表1、表2所示。 將表1、表2參數代入式(14)中,可得系數矩陣參數為 CANbus網絡因素參數選取如表3所示,設定系統采樣周期為10 ms,可得離散系統參數為 表1 碳纖維經紗材料參數Table 1 Material parameters of carbon fiber warp 表2 碳纖維角聯織機系統參數Table 2 Parameters of carbon fiber diagonal loom E2=[0.085 -0.032 0.079],G=[-0.028 -0.053]。 網絡誘導時延d(k)和τ(k)的長度如圖7所示,數據包傳輸情況如圖8所示。 首先,對織機張力系統在理想環境下的工作進行仿真實驗,在該仿真場景中,考慮織機CANbus網絡的時延、丟包及系統的外部擾動均為0,通過本章中控制策略求解可得系統的H∞控制器增益矩陣和觀測器的增益矩陣分別為 采用文獻[3]控制策略所求的的控制器增益矩陣、觀測器增益矩陣分別為 圖7 CANbus通信網絡中網絡誘導時延的長度Fig.7 Length of network induced delay in CANbus communication network 表3 網絡因素參數Table 3 Network factor parameters 圖8 CANbus通信網絡中數據包傳輸情況Fig.8 Data packet transmission in CANbus communication network 系統狀態響應曲線如圖9所示,可以看出,在該情況下,控制策略1和控制策略2均可使系統在0.3 s附近收斂到期望值,二者均實現對織機張力系統穩定控制,但控制策略1相較控制策略2狀態抖動更小。 控制策略1為本文策略所求的控制器;控制策略2為文獻[3] 中的控制策略圖9 理想環境下織機張力系統狀態響應曲線Fig.9 State response curve of loom tension system in ideal environment 第二組仿真實驗中,只考慮系統中存在網絡的隨機時延與數據丟包干擾,通過本文策略求解可得系統的H∞控制器增益矩陣和觀測器的增益矩陣分別為 采用文獻[3]控制策略所求得系統的控制器增益矩陣和觀測器增益矩陣分別為 織機張力系統狀態響應曲線如圖10所示。可以看出,控制策略1作用下系統的狀態響應曲線仍可實現快速收斂,且準確跟蹤期望狀態,而控制策略2作用下系統的狀態響應曲線受網絡干擾影響,產生了明顯抖動,無法對期望狀態準確跟蹤,始終存在跟蹤誤差。這是因為本文策略在設計過程中考慮了控制模型中的時延與丟包的不確定因素,從而對網絡干擾產生了較好的魯棒性。 圖10 網絡因素干擾下織機張力系統狀態響應曲線Fig.10 State response curve of loom tension system under network factors disturbance 在最后一組仿真實驗中,考慮織機在開口機構擾動及網絡因素干擾同時存在的環境下工作,通過本文策略求解可得系統的H∞控制器增益矩陣和觀測器的增益矩陣分別為 采用文獻[3]控制策略所求得系統的控制器增益矩陣和觀測器增益矩陣分別為 其系統狀態響應曲線如圖11所示。可以看出,控制策略1可在1.2 s附近實現狀態收斂,且可在1.2 s之后無抖動的準確跟蹤系統期望狀態,而控制器2作用下的系統狀態則無法實現收斂,系統狀態始終存在較大抖動,且在后期系統狀態有加劇發散的趨勢。這驗證了控制策略1對織機實際工作中存在的CANbus網絡干擾及開口機構擾動均有較強的魯棒性,可滿足CANbus網絡環境下的碳纖維角聯織機的恒張力控制性能要求。 圖11 CANbus網絡環境下織機張力系統狀態響應曲線Fig.11 State response curve of loom tension system in CANbus network environment 對CANbus通信網絡環境下的碳纖維角聯織機張力控制進行了深入研究。將網絡化控制思想應用到了碳纖維角聯織機的張力控制,建立了其網絡化控制模型,不僅考慮了傳感器到控制器的時延,同時也考慮了控制器到執行器的時延,將時變時延的不確定性轉化為了系統參數矩陣的不確定性,并用Bernoulli隨機分布序列描述了系統丟包過程,引入了系統的最優H∞性能指標,通過Lyapunov泛函和CCL迭代算法給出了H∞最優控制器及其觀測器的設計方法。仿真結果表明,所提出的網絡化最優H∞控制算法可實現張力系統狀態的快速收斂并顯著降低狀態抖動,驗證了其對碳纖維角聯織機實際工作中存在的開口系統擾動、網絡因素干擾具有良好的魯棒性,說明該控制算法能夠實現經紗恒張力控制。

2.2 系統穩定性分析

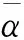






2.3 基于觀測器的最優H∞控制器設計

3 仿真分析
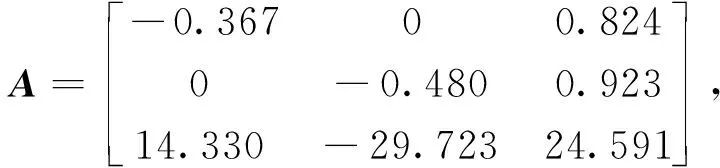
















4 結論

