COSMIC-2掩星反演數據質量分析

薛子悅，鮑艷松，唐歌實，成巍，朱孟斌，袁帥

(1.南京信息工程大學氣象災害預報預警與評估協同創新中心/中國氣象局氣溶膠與云降水重點開放實驗室/氣象環境衛星工程與應用聯合實驗室，江蘇 南京210044；2.南京信息工程大學大氣物理學院，江蘇 南京210044；3.南京信息工程大學，江蘇 南京210044；4.北京應用氣象研究所，北京100029)

1 引 言

無線電掩星技術起源于天文學中的掩星現象，最早被用于太陽系中其他行星的大氣探測。在宇宙探索初期，研究學者發現無線電波信號在經過行星大氣層時會產生系統延遲和偏折，而這種系統性的偏折正是由于大氣中介質的垂直折射指數變化引起的，包含著大氣層的信息。而利用人造地球衛星的無線電掩星探測技術來獲取地球大氣信息的思想最早是在上世紀六十年代由美國噴氣推進實驗室JPL提出[1-2]，經過不斷的技術演變，人們通過在近地軌道(Low Earth Orbit,LEO)衛星上安裝一個雙頻接收機來接收GNSS(Global Navigation Satellite System)信號，獲取由傳播介質的垂直折射指數變化而帶來的信號延遲，得到大氣參數信息。以此為原理的掩星探測技術誕生并迅速發展起來。作為二十一世紀最先進的空間探測技術之一，無線電掩星探測技術不同程度地克服了氣象學領域中傳統觀測的一些弊端，可獲得全球大氣折射率、溫度、氣壓等中性大氣參數廓線，是一項準實時、全球覆蓋、精度高、垂直分辨率高、成本低的創新性技術。

氣象、電離層和氣候衛星聯合觀測系統(Constellation Observing System for Meteorology Ionosphere and Climate,COSMIC)于2006年發射六顆近地軌道衛星，經過產品驗證，其中性大氣產品具有較高的精度水平[3]，可成為研究大氣變化的高精度資料[4]和提升數值預報水平的重要輸入[5]。在經過十四年的運行后，COSMIC-1任務衛星于2020年5月1日退役。美國NOAA與中國臺灣NSPO共同將六顆FORMOSAT-7/COSMIC-2(F7C2)掩星任務衛星送入傾角為24°的低地球軌道，取代退役的COSMIC-1任務衛星。其上主要有效載荷名為TGRS(Tri-GNSS Radio-occultation System)，能接收GPS和GLONASS兩個導航系統的L1和L2信號，并且達到了迄今為止掩星探測載荷的最高信噪比，比COSMIC-1的平均值高出約兩倍。高信噪比不僅提高了大氣廓線的反演質量，令以往產生較大誤差的低緯度帶、低對流層樣本的精度有所提高，也使得觀測數量有了大幅的增加，更有利于科學研究和業務應用。目前國際上掩星計劃均存在由于水汽影響而造成廓線精度不同程度下降的問題，使得掩星數據在低對流層的應用受限。利用高信噪比載荷觀測的COSMIC-2理論上可提升這方面的數據精度。但目前國內對于COSMIC-2掩星數據的反演與分析研究還較少，尚未獲得很好的應用。因此，對于COSMIC-2數據反演以及質量驗證和分析，尤其是對低緯度帶、低對流層的廓線樣本精度進行評價，顯得尤為重要。

本文基于CDAAC(COSMIC Data Analysis and Archive Center)公布的2019年10月—2020年9月COSMIC-2 conPhs大氣附加相位L1b數據，利用無線電掩星數據處理軟件ROPP(the Radio Occultation Processing Package)反演大氣廓線。首先采用幾何光學和波動光學方法反演大氣折射率廓線，再通過折射率一維變分同化得到溫濕廓線。以探空站點資料作為參照，將反演的折射率、溫濕廓線結果分不同緯度、不同季節進行了統計驗證和精度分析。同時，與COSMIC-2的wetPf2二級數據進行對比，對反演數據的優劣進行討論。

2 數據與方法

2.1 數據介紹

本文采用每日發布的conPhs大氣附加相位L1b數據作為反演輸入數據，日均可獲取四千余個掩星觀測樣本。由于COSMIC-2目前在軌的六顆衛星均處于低傾角(24°)軌道，因此所用的探測數據的地理覆蓋范圍僅在45°S～45°N緯度帶之間。探測的基本參數是GNSS無線電載波信號的振幅、相位以及導航衛星與低軌衛星的位置信息。

2020年5月之后的conPhs數據文件中不再存放以100 Hz頻率記錄的衛星位置信息，而是每秒僅記錄一次。因此，為了對COSMIC-2進行數據反演和分析，本文將文件中的衛星位置坐標分別插值到了100 Hz的頻率上，并使用插值后的位置坐標的斜率計算出衛星運行速度，重新創建完整的conPhs文件。

wetPf2數據為COSMIC-2官方公布的二級產品，CDAAC以COSMIC-2掩星探測結果(彎曲角和折射率)作為觀測量，以歐洲中期天氣預報中心ECMWF發布的再分析數據ERA-Interim作為背景先驗信息[6]，使用一維變分方法來反演大氣溫度、濕度和壓強[7]。Chen等[8]以無線電探空儀數據為標準進行精度驗證，得出wetPf2產品在0～15 km范圍內溫度和水汽壓標準差分別為1.3～1.5 K和0～2.2 hPa的評價。

2.2 反演流程

當GNSS信號發射機從高空發射的無線電信號穿過大氣層時，由于大氣中介質垂直密度分布的變化，信號傳播路徑會發生一定的偏折。偏折前后產生一個彎曲角α，根據這一彎曲角可利用積分變換計算大氣折射率。本文所用的conPhs大氣附加相位L1b數據可提供單次掩星事件的大氣附加相位、信噪比、衛星位置和速度等輔助數據，在經過對附加相位數據的濾波、質控后，采用幾何光學和波動光學反演方法進行彎曲角的計算。在局部球對稱的假設下，該彎曲角可與碰撞參數a(定義為折射中心點到信號射線的垂直距離)建立起唯一的對應關系。在去除電離層效應并統計優化后，使用Abel積分變化將彎曲角轉換為大氣折射率。再利用ECMWF再分析數據作為背景場數據，進行掩星折射率一維變分同化反演，得到大氣溫濕廓線。本文使用ROPP掩星數據處理軟件實現上述反演流程。

ROPP掩星數據處理軟件由歐洲氣象局無線電掩星氣象衛星應用機構(ROM SAF)開發，用于掩星觀測數據處理與反演，可適用于世界上幾乎所有掩星觀測計劃發布的數據。王大釗等[9]利用ROPP成功地進行了無線電掩星數據反演，與二級產品進行對比，得到的折射率和濕度相對誤差在2%以內，溫度誤差不超過2 K。參照其反演流程進行實驗設計，給出所用軟件模塊進行反演的主要流程圖(圖1)。

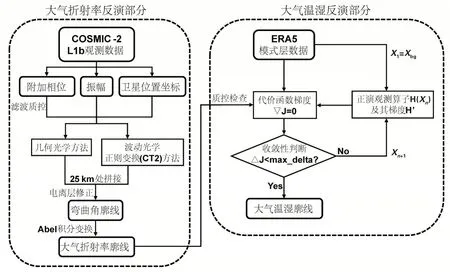
圖1 反演流程圖

在大氣折射率反演部分，主要使用處理模塊中的ropp_pp_occ_tool工具[10]得到折射率結果。該部分首先對L1和L2雙頻信號觀測的附加相位和振幅進行濾波降噪等質量控制[11]，在信號跟蹤誤差非常大的情況下，會對數據進行截斷并舍去。相比于L1信號，L2信號的信號跟蹤誤差更大，利用MSIS全球氣候學模型計算得到的模型信號值來代替L2信號[12]。對預處理后的雙頻信號采用幾何光學[13]和波動光學(正則變換CT2算法[14])方法反演彎曲角廓線，兩種方法反演的結果在25 km左右高度處拼接。25 km以下采用波動光學反演結果，可更好地減小在低對流層由于水汽增多引起的多路徑效應影響。為了去除彎曲角廓線結果中存在的電離層噪聲貢獻，應用電離層校正算法，結合實測和氣候彎曲角數據，通過統計優化來降低噪聲[11]。最后，利用Abel積分變換[15]的逆變換公式將彎曲角α轉換為折射率N。

在大氣溫濕反演部分，主要使用折射率一維變分模塊中的ropp_1dvar_refrac工具[16]得到大氣溫濕結果。對以下代價函數進行求解：

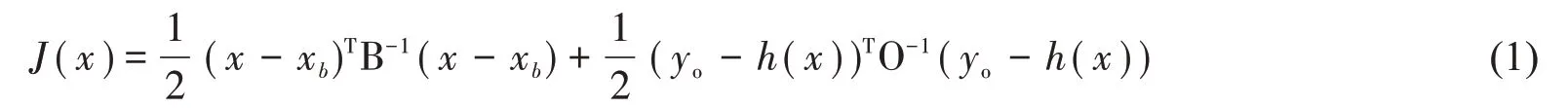
其中，x為大氣狀態向量的最大似然解；觀測場yo為反演得到的大氣折射率數據；背景場x b選擇137層的ERA5模式層數據；背景誤差協方差B和觀測誤差協方差O選用ROPP提供的對應層數的誤差信息文件；正演算子h(x)的基本表達式采用Smith公式[17]。盡管許多學者基于Smith公式進行了更多研究，以得到精度更高的表達式，但Smith公式仍然是GPS氣象領域廣泛采用的折射率“標準”表達式[18]。利用基于擬牛頓法[19]的ROPP極小化工具對代價函數進行極小化求解，得出最優大氣狀態參量。

2.3 反演結果檢驗方法

利用美國懷俄明大學網站提供的探空站點資料作為參考真值，對反演結果進行對比驗證[20]。由于探空站點數據時間相對固定(每日00 UTC和12 UTC)，而掩星觀測數據的時空分布較為隨機，所以對兩者進行統計比較時，觀測時間和位置必須匹配至合理范圍內。匹配原則參考Kuo等[20]的做法，首先將兩者觀測時間差控制在±1 h內，再以探空站點的位置為中心，周圍100 km范圍內匹配掩星樣本點。圖2顯示了2019年12月21日單日樣本的時空匹配情況，將匹配好的數據對進行位勢高度上的插值。設定高度層范圍為0～35 km，分辨率為0.1 km，共350層。對于在整個高度層上存在部分缺測的樣本數據，仍保留廓線，利用有數據的部分高度層加入統計。2019年10月—2020年9月共得到3 689對匹配樣本。

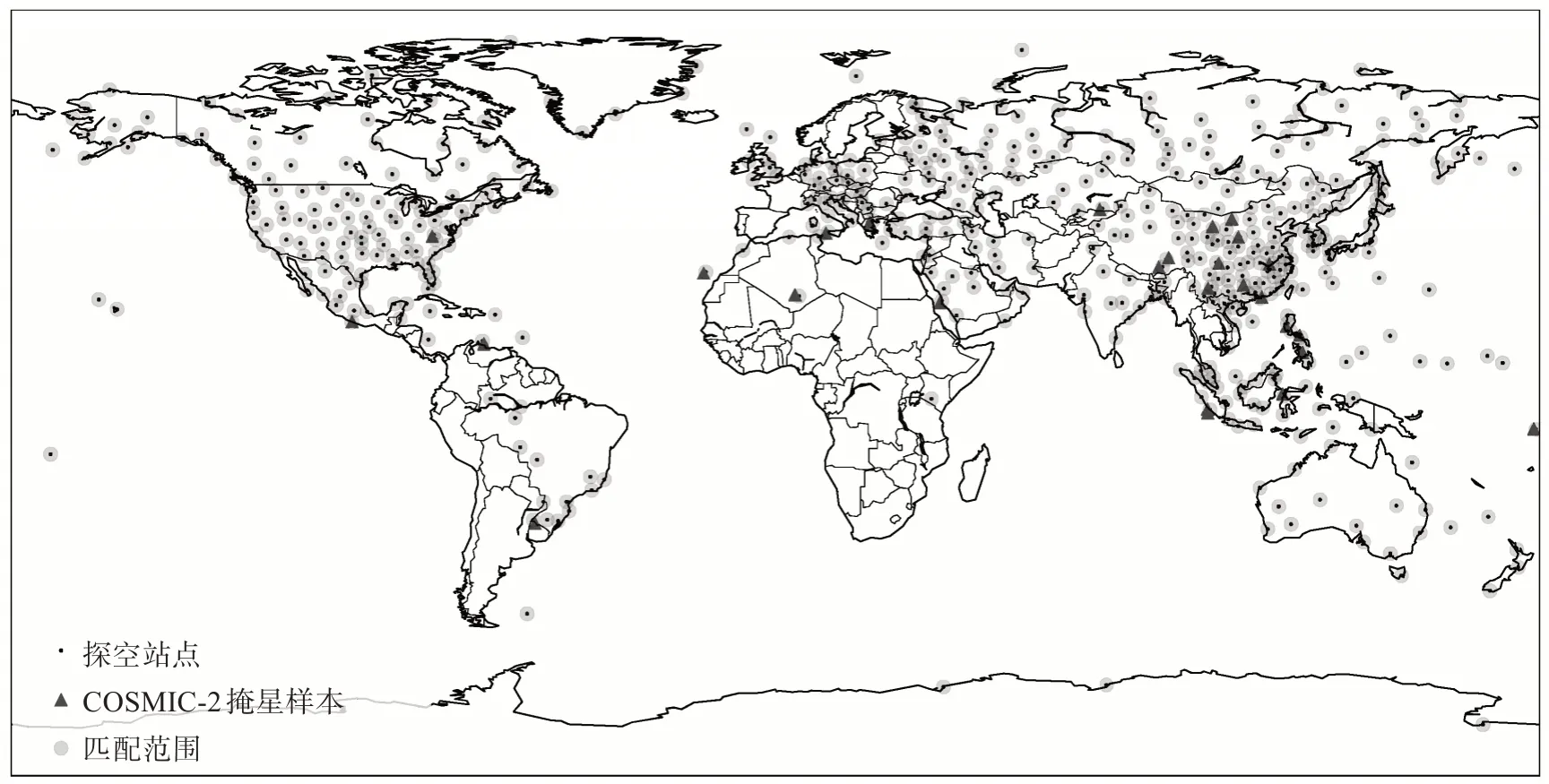
圖2 2019年12月21日COSMIC-2與探空站點數據全球匹配情況

進行對比驗證的大氣參量為大氣折射率、大氣溫度和相對濕度廓線。由于探空站點沒有直接的折射率數據提供，故在對COSMIC-2反演折射率數據進行質量分析之前，先將探空資料由提供的溫度、氣壓、水汽混合比轉換為折射率參數：

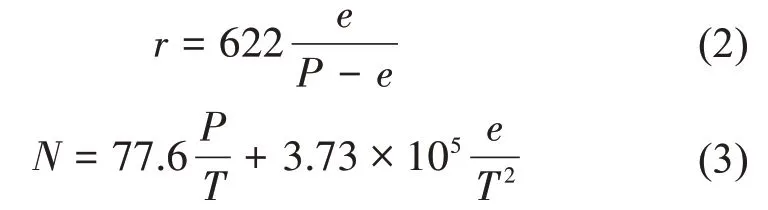
其中，r為水汽混合比(g/kg)，P為大氣壓強(hPa)，e為水汽壓強(hPa)，T為溫度(K)，N為大氣折射率。

同時，將反演的比濕廓線結合溫度和氣壓，轉換為相對濕度廓線：

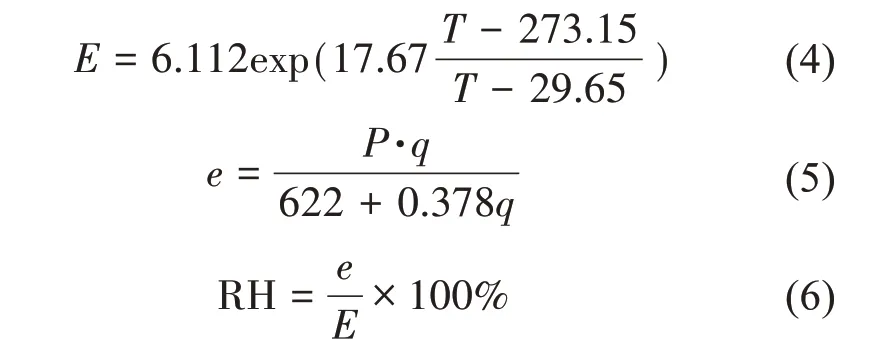
其中，T為溫度(K)，E為溫度T時的飽和水汽壓(hPa)，P為大氣壓強(hPa)，q為比濕(g/kg)，e為水汽壓強(hPa)，RH為相對濕度。

為保證數據質量，在對比分析前對探空站點和反演數據分別進行質控。對折射率數據的質控手段主要有兩步。第一步進行極值檢查：根據大氣折射率極值范圍，將存在折射率值小于0或大于400的廓線樣本剔除；第二步進行單調性檢查：根據大氣折射率與高度的指數關系[21]，若單個廓線樣本中，折射率隨高度增加而不單調遞減的高度層超過總高度層數的20%，則剔除該廓線。經過上述質控，剔除約14%的樣本量。大氣溫度和相對濕度采用折射率質控后的對應樣本進行統計。

在對比分析中，折射率采用平均相對偏差MRE和相對偏差標準差STD來驗證精度，分別由公式(7)、公式(8)和公式(9)得到；大氣溫度和相對濕度采用平均偏差ME和均方根誤差RMSE來驗證精度，分別由公式(10)和公式(11)得到。i表示第i個廓線樣本，n為統計樣本數，x代表統計量，即大氣溫度和相對濕度，RO和Sound分別代表掩星反演得到的和探空站點的數據。

在分緯度帶對比分析中，將反演結果樣本分為南北緯0°～15°、15～30°、30～45°三個緯度帶；在分季節對比分析中，將反演結果樣本根據掩星點的緯度區分為南北半球，并以不同月份劃分四季：北半球3—5月和南半球9—11月為春季，北半球6—8月和南半球12—2月為夏季，北半球9—11月和南半球3—5月為秋季，北半球12—2月和南半球6—8月為冬季。

3 反演結果與分析

3.1 大氣折射率廓線

3.1.1 整體驗證

圖3和圖4從整體上驗證了COSMIC-2數據反演的大氣折射率的精度。圖3為探空數據與反演折射率數據在0～35 km范圍內選取的九個高度層上的散點對比圖，各層的數據點分布在y=x參考直線兩側，大部分高度層上反演折射率比探空折射率略小，相關系數在0.663～0.967之間，其中15 km高度層最優，在2 km和35 km高度附近負偏差較明顯。2 km及以下高度大氣中超折射現象增多，應用算法中的Abel積分變換導致了負偏差[22]；而35 km高空則可能在電離層校正和降噪過程中對彎曲角的不當加權，導致優化的彎曲角存在一定偏差，這一偏差最終進入到了折射率結果中[23]，這與折射率相對偏差在平流層中通常隨高度增加而增大的事實[22]相符。總體上各高度層偏差不大，說明反演折射率與探空折射率之間有很好的一致關系。

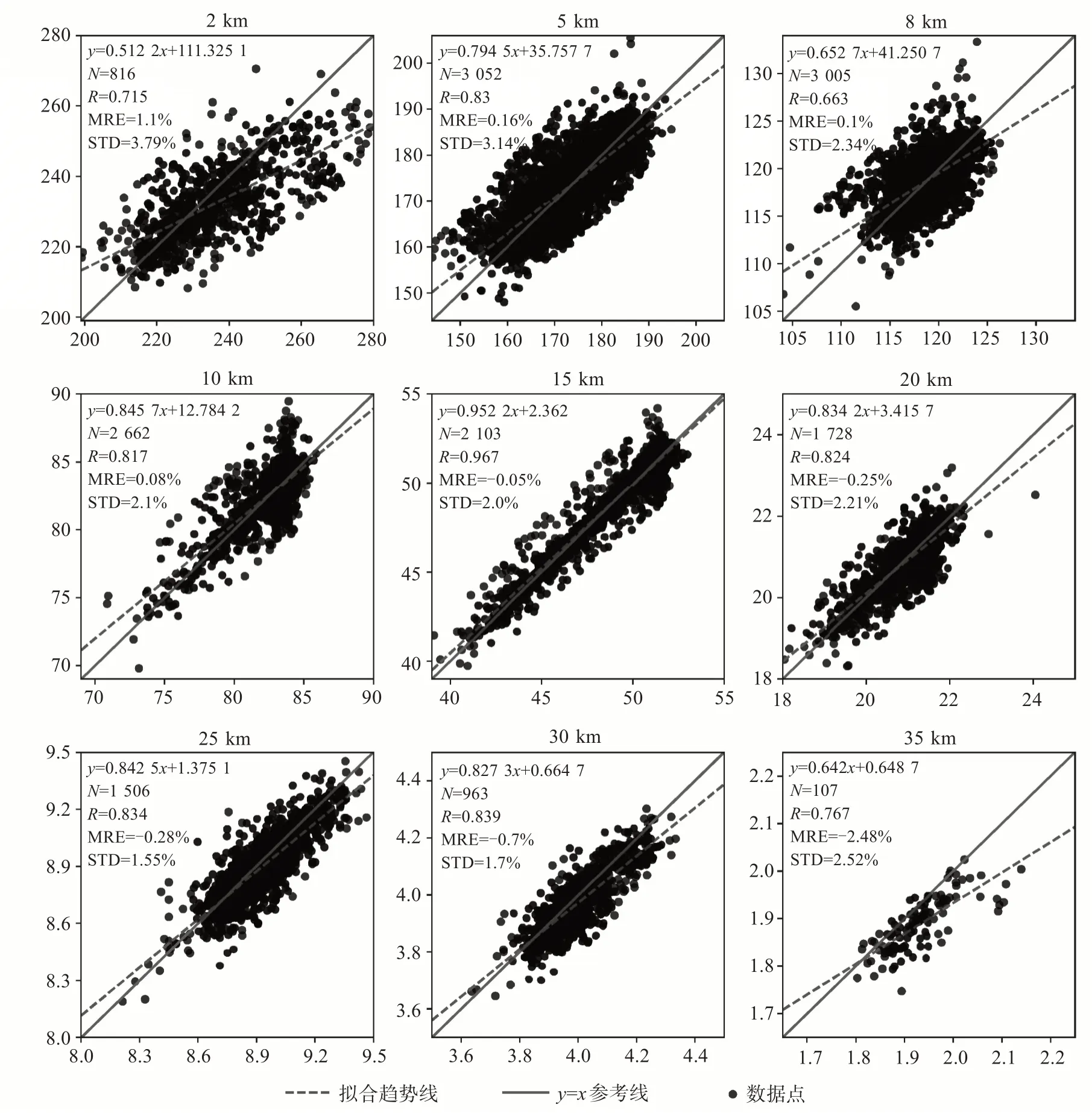
圖3 探空數據(橫坐標)與COSMIC-2反演折射率(縱坐標)不同高度層處散點圖 單位：N-units。

圖4為反演大氣折射率與wetPf2二級產品折射率數據的平均相對偏差(MRE)和相對偏差標準差(STD)圖，retri代表反演折射率，wetL2代表二級產品折射率，樣本數量為掩星樣本和探空樣本在不同高度上匹配后得到的樣本分布情況。從反演折射率的整體統計結果來看，MRE在-2.5%～0.5%以內，整體上反演折射率略低于探空站點折射率，5 km以下和25 km以上均以負偏差為主，低層最大負偏差為1 km處的-2.2%，隨高度升高至5 km處的0.3%，在5～25 km高度層上始終穩定保持在±0.5%以內，25 km以上又顯示出負偏差的趨勢；STD整體上在1.5%～4.3%，最大出現在1 km處為4.3%，隨高度升高逐漸減小，至35 km都維持在3%以內，最小值出現在25 km處為1.5%；不同高度層的統計樣本數量在5～10 km內最多且穩定，5 km以下樣本數量減小是因為掩星探測高度有限，在一些多水汽的情況下無法探測到低層；而由于探空折射率數據在質控后越往高層越容易出現缺測誤測的情況，導致了10 km以上樣本匹配數量的減少。

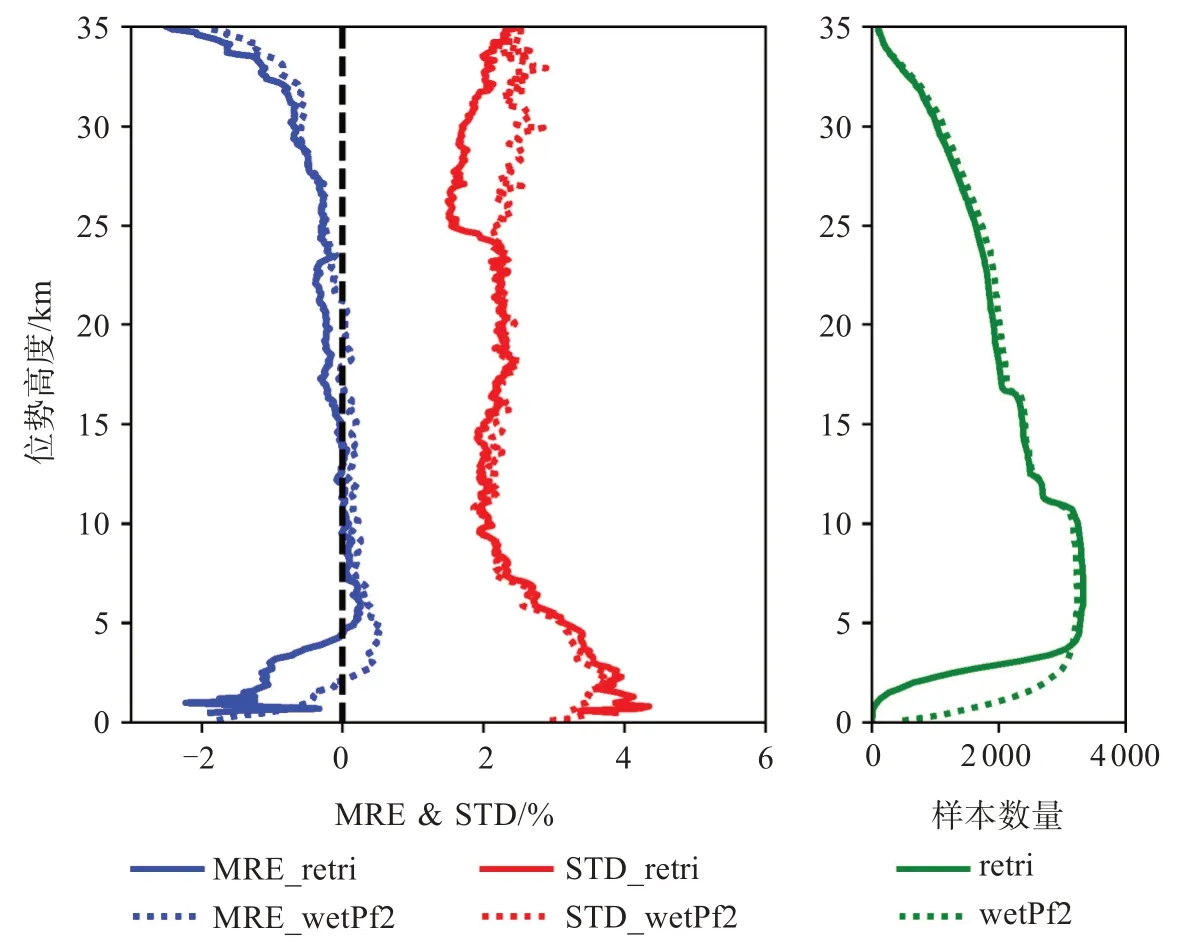
圖4 折射率廓線平均相對偏差和相對偏差標準差圖

從反演折射率與產品折射率的對比上來看，兩者都保持在較高精度水平且都存在一定的負偏差，但反演折射率5 km以下的負偏差比產品折射率更大，在5～30 km內更小；在24 km以上反演折射率STD明顯小于產品折射率STD，而在24 km以下差距不大。造成這種結果的原因可能是對于L2信號的處理不同：在ROPP中采用MSIS模型作為L2信號的模型代替值，CDAAC則采用CIRA+Q模型[24]，兩種模型之間的差異可能導致了折射率STD的差異。同時，25 km附近是反演折射率兩種方法結果的拼接高度，這一高度以下當L2信號噪聲過大時將不再使用L2信號加入反演過程中，因此僅在24～35 km中差異較大。兩者統計樣本數量在5 km以上趨近一致，但在5 km以下產品折射率樣本的數量更多。

3.1.2 分緯度驗證

圖5為反演的大氣折射率按緯度劃分的平均相對偏差和相對偏差標準差圖，從分緯度帶對比平均相對偏差中可以看出，在5 km以下，各緯度帶樣本均有不同程度的負偏差，且緯度越低，負偏差越大，最大負偏差出現在15°緯度帶樣本中，為-4%；在5～25 km內各緯度帶樣本差距不大，三類樣本的MRE均在±0.5%以內；25 km以上的負偏差也以15°緯度帶樣本最為明顯。從分緯度帶對比相對偏差標準差中可以看出，5 km以下15°緯度帶樣本的STD最小，30°緯度帶樣本的STD最大；在5 km以上均顯示出緯度越低，STD越小的趨勢，特別是在8～16 km高度層上，三類樣本STD的差距相對較大。因此可以看出，COSMIC-2低緯度樣本的折射率精度都一定程度地優于中緯度樣本，且在不同高度層上呈現不同差距。

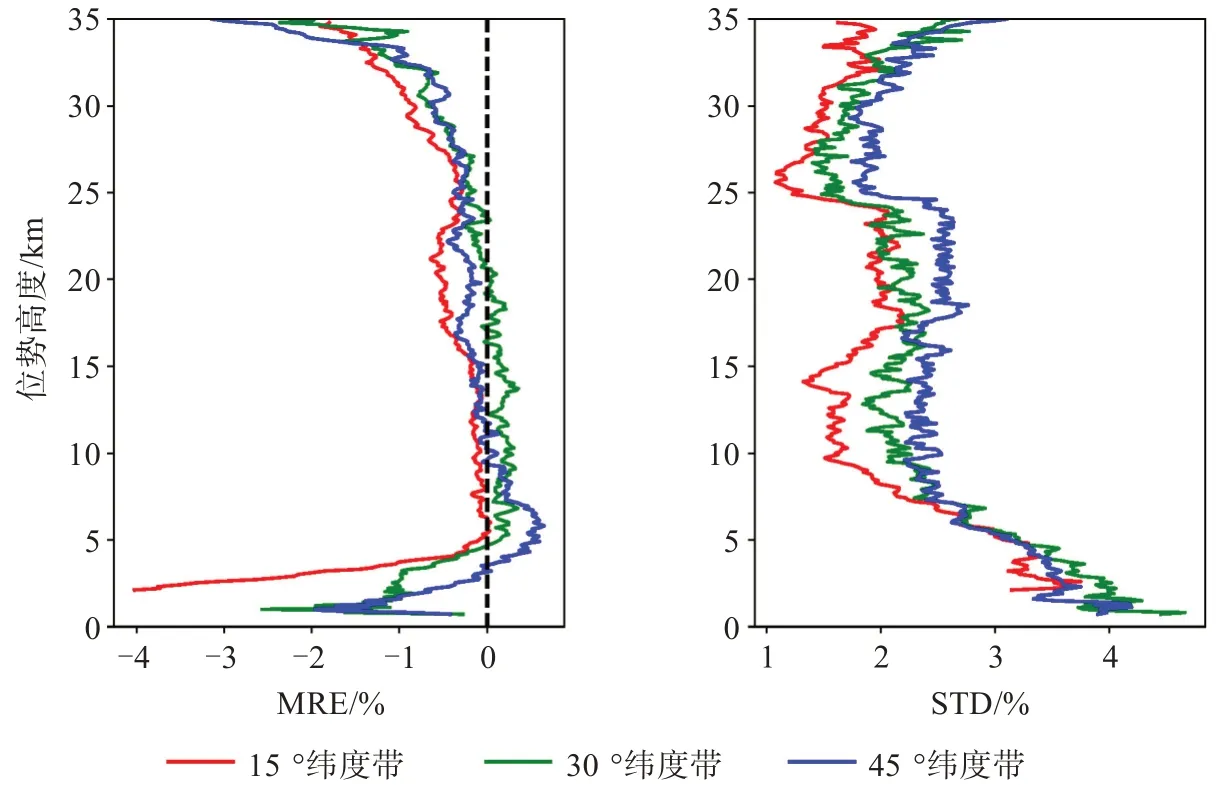
圖5 折射率廓線按緯度劃分的平均相對偏差和相對偏差標準差圖

3.1.3 分季節驗證

圖6為反演的大氣折射率的按季節劃分的平均相對誤差和相對偏差標準差圖，從分季節對比平均相對偏差中可見，夏季在5 km以下的低對流層負偏差最明顯；5～15 km四類樣本差距不大，均在±0.3%內；25 km以上的負偏差又以夏季最明顯。從分季節對比相對偏差標準差中可見，18 km以下夏季折射率STD始終為四類樣本中最大，秋季樣本次之，冬季和春季最小；尤其在3 km以下，夏季折射率STD最大可達5.5%，冬季樣本最優；而在20 km以上，四類樣本STD變化則顯示出較高的一致性。出現以上現象的主要原因是，在夏季低層尤其是低對流層水汽較多，造成了較大的折射率梯度，對掩星無線電信號產生較大影響，導致了相對較大的誤差。

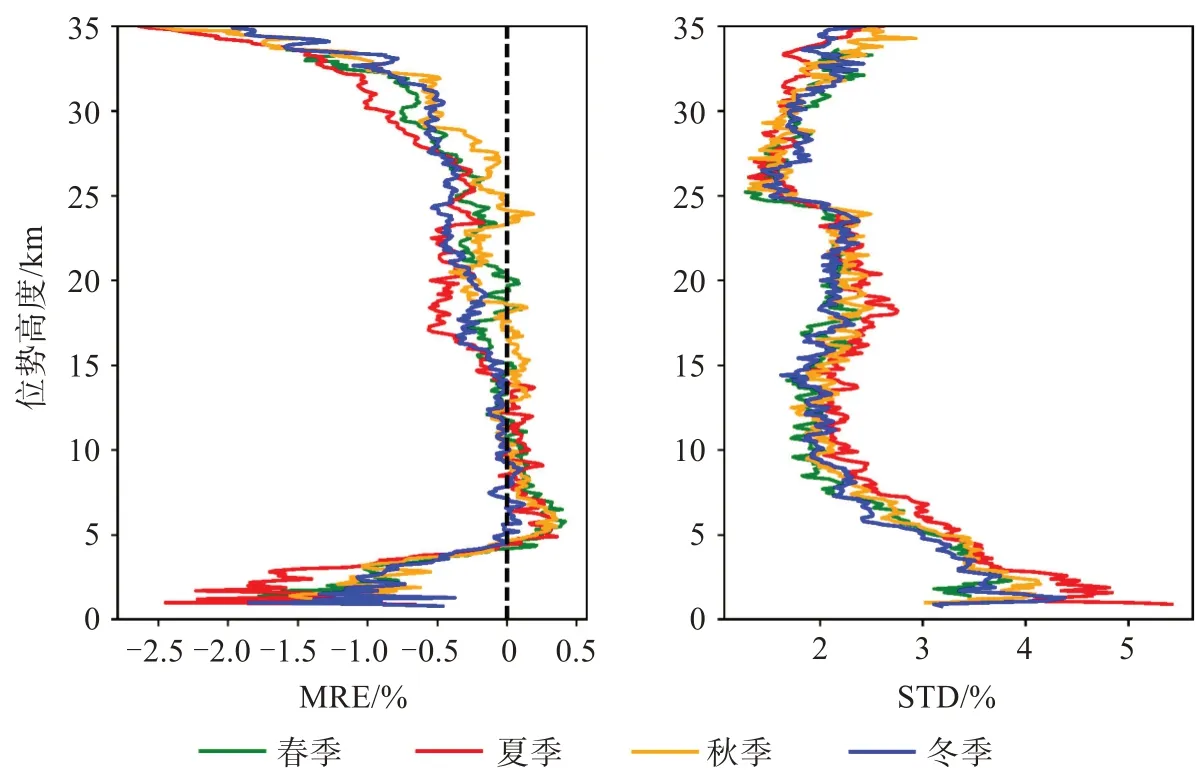
圖6 折射率廓線按季節劃分的平均相對偏差和相對偏差標準差圖

3.2 大氣溫度廓線

3.2.1 整體驗證

圖7和圖8從整體上驗證了COSMIC-2數據反演的大氣溫度的精度。圖7為探空數據與反演溫度數據在0～35 km范圍內選取的九個高度層上的散點對比圖。反演溫度與探空溫度在大部分高度層上偏差不大，相關系數總體在0.677～0.939之間，2 km處最優，25 km處最差，相關系數的下降可能與掩星觀測和探空觀測越往高層水平漂移越大有關。對流層溫度誤差相對更小，RMSE可達到1.5 K以內；平流層溫度誤差相對較高，但整體上RMSE均不超過2.5 K。

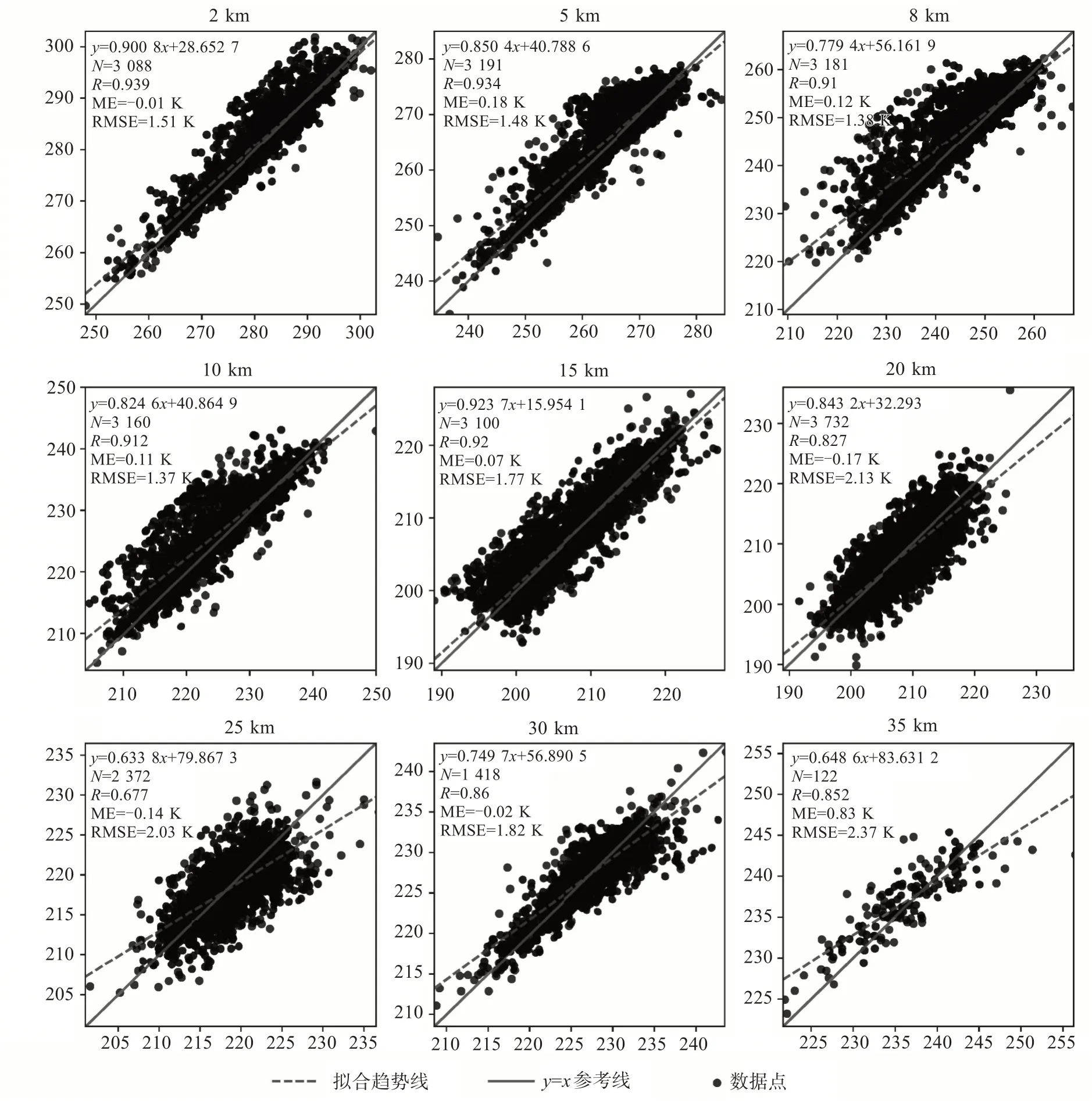
圖7 探空數據(橫坐標)與COSMIC-2反演溫度(縱坐標)不同高度層處散點圖 單位:K。

圖8為反演大氣溫度與wetPf2二級產品溫度數據的平均偏差(ME)和均方根誤差(RMSE)圖。從反演溫度的整體統計結果來看，ME整體上在±0.5 K以內，低層0～2 km以負偏差為主，最大為0.3 km處的-0.4 K，隨高度升高至4 km處的0.2 K，在4～12 km高度層上穩定在0.2 K左右，之后開始減小，從15 km開始往上到30 km再次變為負偏差，最大達-0.3 K；RMSE整體上在1.3～2.2 K，0～14 km高度處穩定保持在1.3～1.5 K，隨后增大至25 km處的2.1 K；不同高度層的統計樣本在2～16 km內數量最多且穩定，這個范圍也是溫度RMSE最小的高度范圍。從反演溫度與產品溫度的對比上來看，兩種數據在各高度層上誤差趨勢很接近，反演溫度的ME絕對值比產品溫度的更小，在0～13 km和27～35 km高度上反演溫度的RMSE比產品溫度更小，且反演溫度的樣本數量在5 km以下的底層更多。因此，反演溫度的精度在大多數高度層上略優于二級產品溫度，這可能是兩種數據進行一維變分同化時所選取的背景場信息不同所導致的。

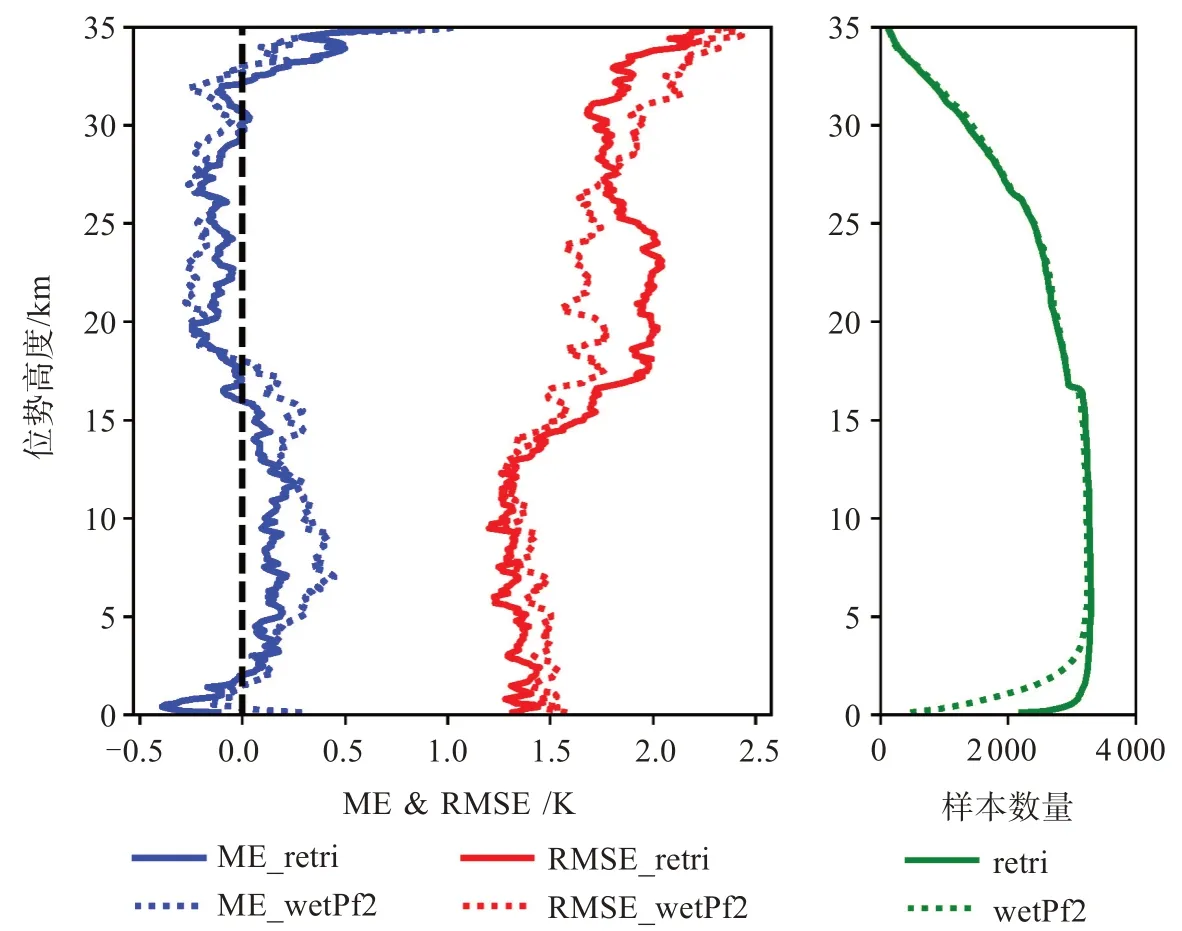
圖8 大氣溫度廓線平均偏差和均方根誤差圖

3.2.2 分緯度驗證

圖9為反演的大氣溫度按緯度劃分的平均偏差和均方根誤差圖。從分緯度帶對比的平均偏差中可以看出，樣本點的緯度越高，ME的絕對值越大；而在17 km以下，15°緯度帶的樣本以負偏差為主，30°和45°緯度帶的樣本以正偏差為主，17 km以上則大致相反。從分緯度帶對比均方根誤差圖中也可以更明顯地看出，樣本點的緯度越高，RMSE越大，廓線精度也越差；三類樣本的RMSE在17 km以上走勢逐漸趨同，而17 km以下則顯示出較大差距；三類樣本在同一高度層的RMSE最大差距在10 km左右處，15°緯度帶樣本RMSE比45°緯度帶樣本小0.8 K左右。因此可以看出，COSMIC-2低緯度樣本的大氣溫度精度優于中緯度樣本，且在對流層差距明顯。

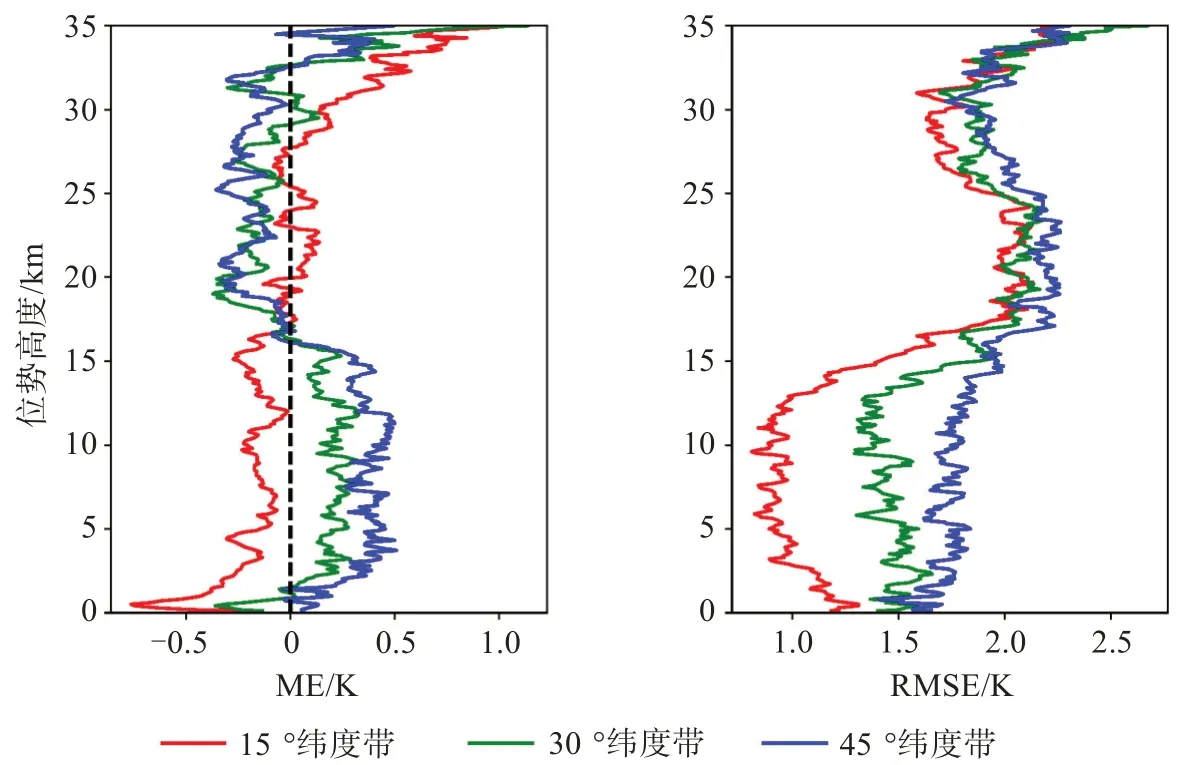
圖9 大氣溫度廓線按緯度劃分的平均偏差和均方根誤差圖

3.2.3 分季節驗證

圖10為反演的大氣溫度按季節劃分的平均相對誤差圖。從分季節對比中可以看出，24 km以上夏季與秋季的溫度ME絕對值略大一些，24 km以下四季樣本ME差異較小；15 km以下秋季樣本RMSE略小于其他三季，15 km以上四季樣本RMSE差異較小。但可以看出，各類樣本在各高度層上的差異較小，溫度的季節性差異不顯著。

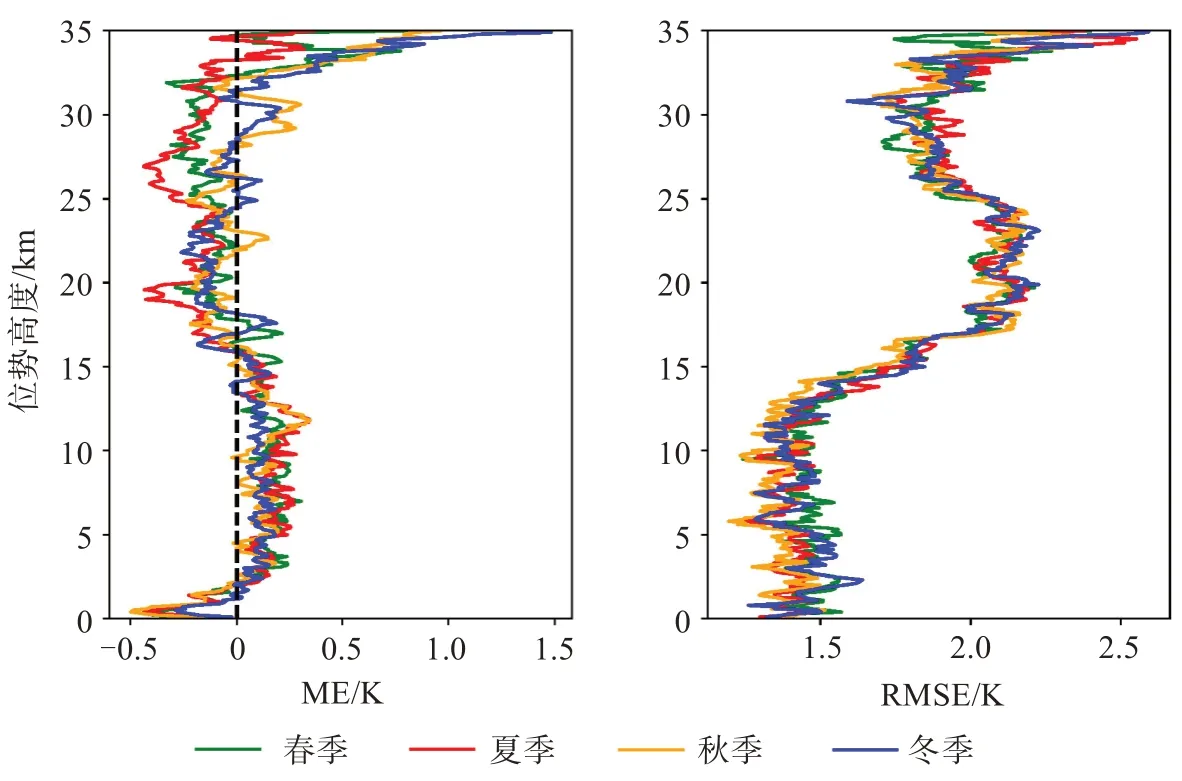
圖10 大氣溫度廓線按季節劃分的平均偏差和均方根誤差圖

3.3 相對濕度廓線

3.3.1 整體驗證

圖11和圖12從整體上驗證了COSMIC-2數據反演濕度的精度。由于大氣中的水汽主要存在于低層，因此本文只統計0～12 km高度范圍內的濕度情況。圖11為探空數據與反演濕度數據在0～12 km范圍內選取的六個高度層上的散點對比圖。反演相對濕度與探空相對濕度各高度層上的相關系數在0.784～0.903，精度隨高度升高逐漸變差，但最大均方根誤差不超過15%。

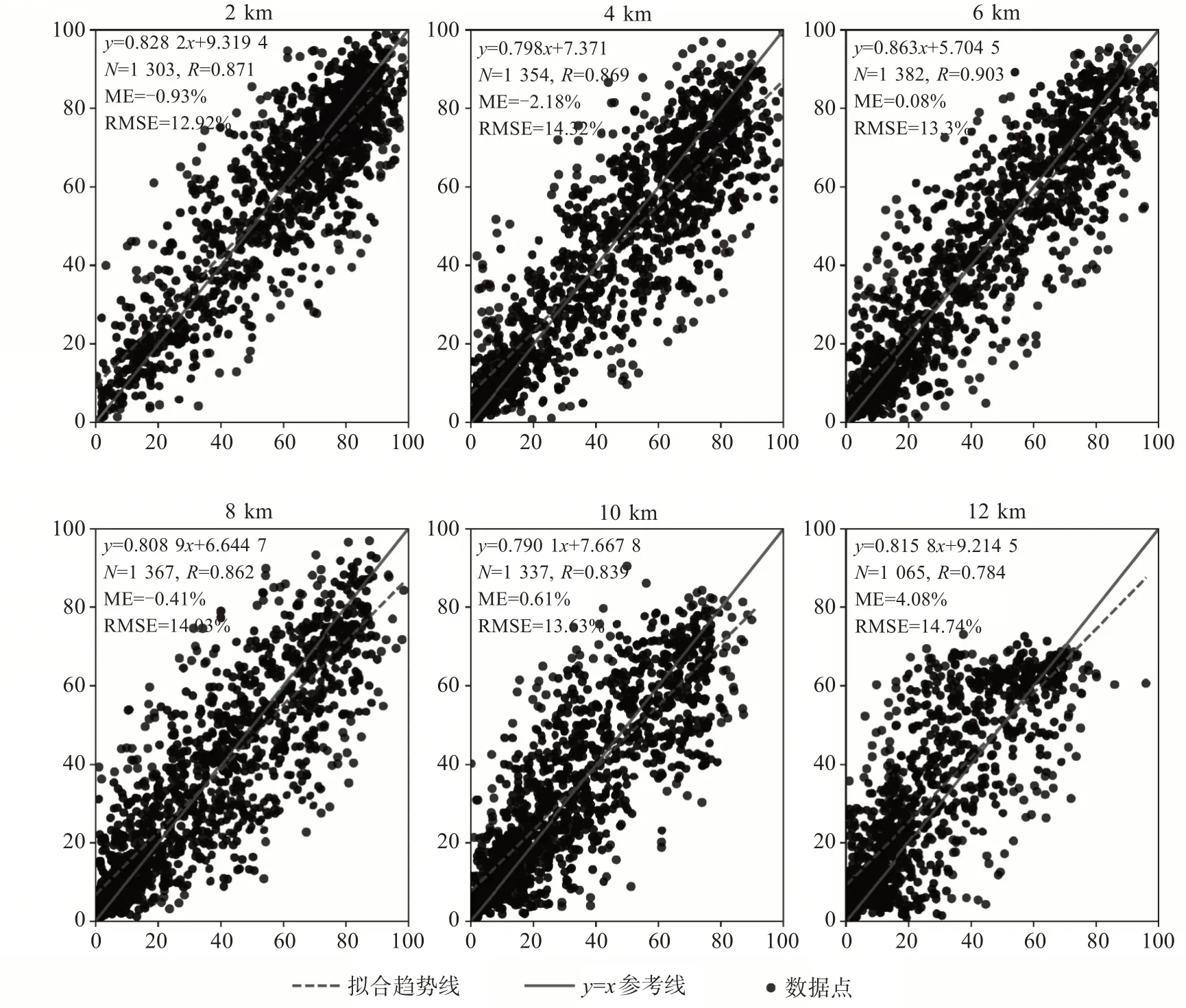
圖11 探空數據(橫坐標)與COSMIC-2反演濕度(縱坐標)不同高度層處散點圖 單位:%。

圖12為反演相對濕度與wetPf2二級產品相對濕度數據的平均偏差(ME)和均方根誤差(RMSE)圖。從反演相對濕度的整體統計情況來看，ME在±5%范圍內變化，隨著高度的升高先由正偏差減小為負偏差，再變為正偏差，且4 km以下的低層偏差絕對值要大于4 km以上的部分；RMSE隨著高度升高逐漸變大，但始終保持在15%以內，具有較高的精度。從反演濕度與產品濕度的對比情況可見，3 km以下兩者ME呈相反走勢，但都在±5%以內，3 km以上反演相對濕度ME明顯小于產品相對濕度；從RMSE上也可看出，反演相對濕度結果優于二級產品，在6 km以上尤為明顯，兩者差距最大可達7%左右；統計樣本數量呈相同趨勢分布，且反演樣本比產品樣本多約50%，但濕度樣本數量相對于溫度來說更少，這可能與濕度反演過程中的質控手段[7]有關。因此，反演相對濕度的精度在整體上都優于二級產品相對濕度，與溫度結果在0～13 km之間反演精度優于二級產品的結論類似。

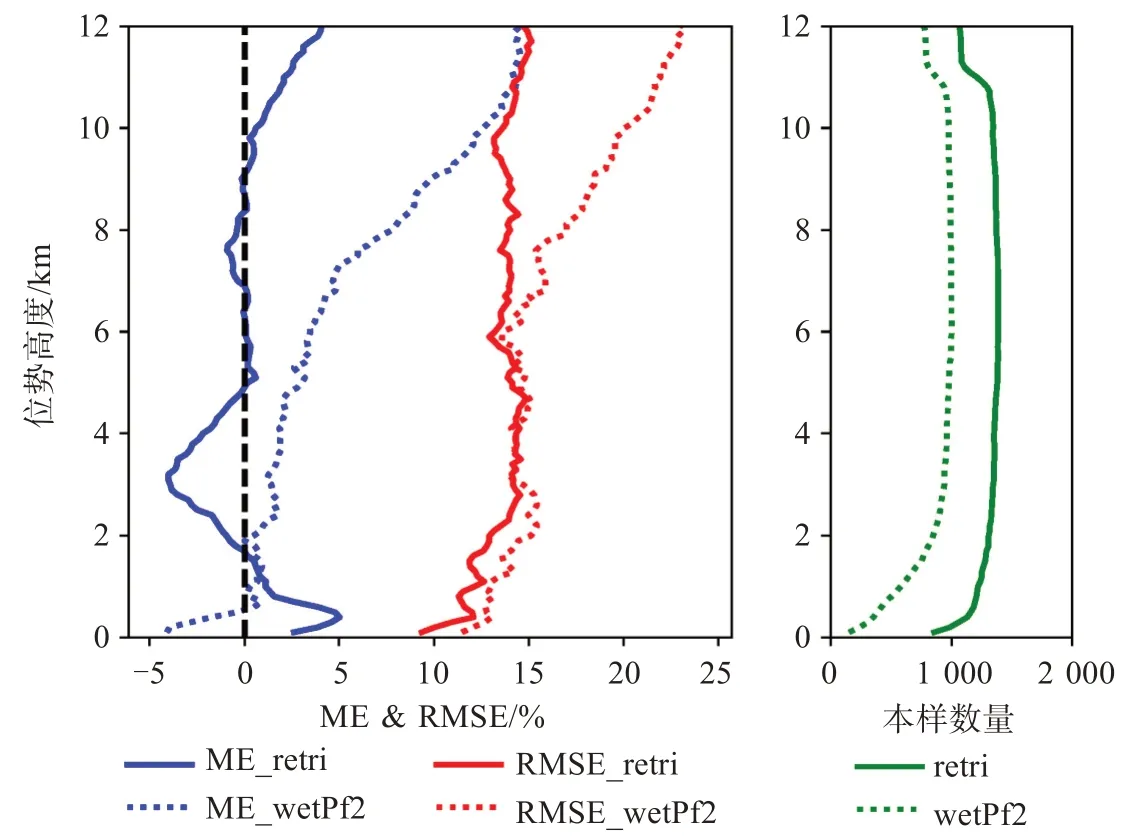
圖12 相對濕度廓線平均偏差和均方根誤差圖

3.3.2 分緯度驗證

圖13為反演相對濕度按緯度劃分的平均偏差和均方根誤差圖，2 km以下相對濕度ME在不同緯度樣本中趨勢類似，在2～5 km高度內15°和30°緯度帶樣本負偏差更明顯，在5 km以上兩者ME絕對值比45°緯度帶樣本都要小；在5 km以下，15°緯度帶樣本在三類樣本中RMSE最小，且在近地面可達10%以內，5 km以上三類樣本則顯示類似的誤差趨勢，差異較不明顯。因此可見，以往掩星探測結果中因水汽造成的較大誤差被縮小，盡管差異不大，但低緯度樣本在低對流層顯示出了更好的精度。

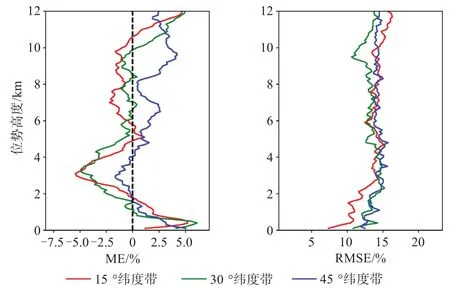
圖13 相對濕度廓線按緯度劃分的平均偏差和均方根誤差圖

3.3.3 分季節驗證

圖14為反演相對濕度按季節劃分的平均偏差和均方根誤差圖。其中冬季樣本的ME絕對值總體上保持最小，夏季最大，其余兩季樣本ME變化差異不大；在4 km以上冬季樣本的RMSE略小于其他三季樣本。因此可見，反演相對濕度樣本在冬季的誤差略小，其余樣本誤差變化的季節性差異并不顯著。

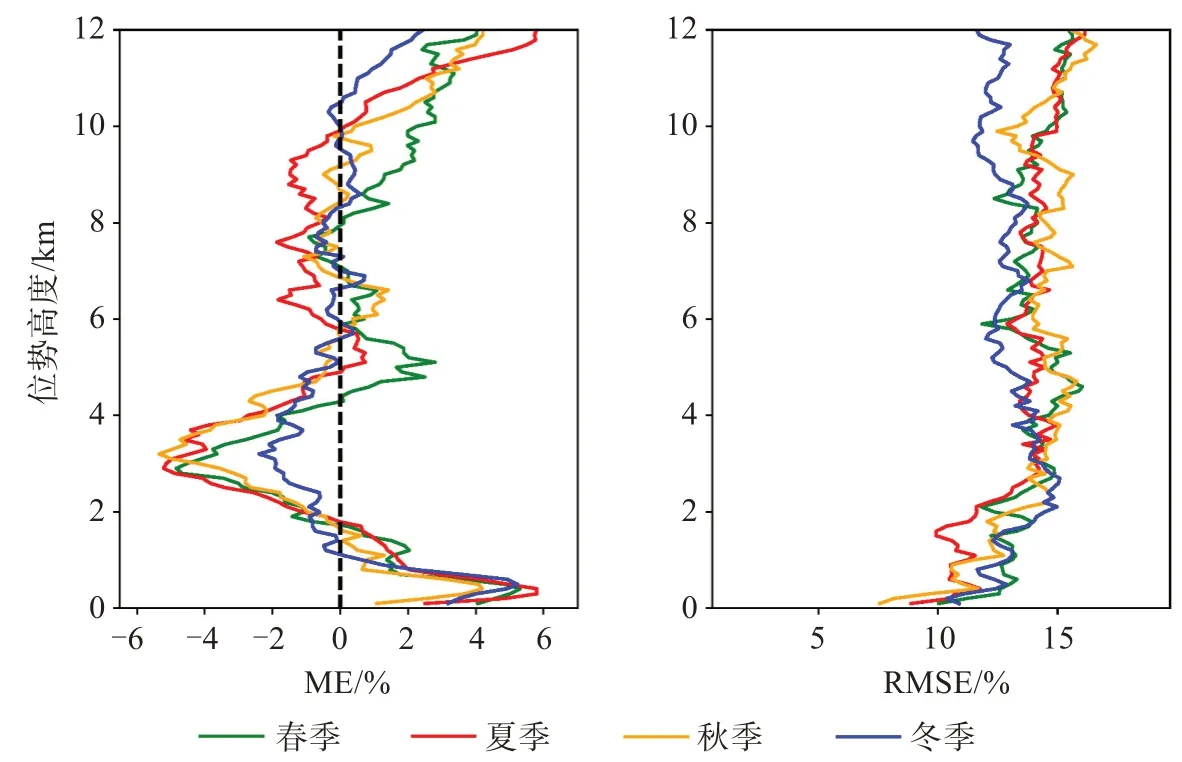
圖14 相對濕度廓線按季節劃分的平均偏差和均方根誤差圖

3.4 誤差原因分析

本文對COSMIC-2數據的反演結果相比于二級產品，在一定程度上取得了更高的精度，但相比于探空觀測資料還有一定的誤差存在。造成誤差的原因可能有：(1)反演數據與探空站點資料時空匹配時仍存在時間和空間位置上的差異。探空氣球上升探測所形成的廓線并不是嚴格垂直的，存在一定的漂移，越往高空漂移量越大；同時，掩星觀測的廓線也存在位置上的水平漂移，實際處理數據中35 km高度范圍內最大水平漂移有10～50 km，兩者在水平漂移方向上的不確定性也會造成一定的誤差；(2)在水汽含量很大的低對流層通常會產生超折射，在此處采用Abel積分變換導致了低層折射率的負偏差。

4 結 論

本文使用COSMIC-2 conPhs大氣附加相位L1b數據，基于ROPP軟件計算得到大氣折射率和大氣溫濕廓線，對上述大氣廓線進行對比驗證和精度分析，得出以下主要結論。

(1)COSMIC-2反演大氣折射率、大氣溫度、相對濕度與探空站點數據對比，在不同高度層上均具有較好的一致性，相關系數最高分別可達0.967、0.939、0.903；反演折射率相對偏差標準差為1.5%～4.3%，反演溫度和相對濕度均方根誤差分別為1.3～2.2 K、10%～15%；反演折射率的精度在24 km以上優于二級產品折射率，反演溫度的精度在0～13 km和27～35 km上優于二級產品溫度，反演相對濕度在整體上都優于二級產品相對濕度。

(2)以探空站點資料為參考，COSMIC-2反演折射率和溫度的精度隨緯度變化顯著，低緯度樣本精度總體上均優于中緯度樣本；反演相對濕度在3 km以下低緯度樣本精度優于中緯度樣本，3 km以上差距不大。表明COSMIC-2數據對低緯度帶觀測的改善顯著，使其精度大大提升，成為各緯度帶中精度最高的樣本。

(3)以探空站點資料為參考，COSMIC-2反演數據的精度隨季節變化不明顯，總體上冬、春季樣本誤差略小于夏、秋季。表明COSMIC-2數據減小了由水汽含量帶來的誤差影響，縮小了夏季樣本與其余季節樣本的精度差距。

致 謝：感謝COSMIC數據分析中心(CDAAC)提供的COSMIC-2掩星觀測數據，感謝南京信息工程大學高性能計算中心的計算支持和幫助。