基于深度森林的高校貧困生認定模型研究

滕玲，施三支，張夢菲，劉先俊

（1.長春理工大學 數學與統計學院，長春 130022；2.長春理工大學 學生工作部，長春 130022）

家庭經濟困難學生的認定是高校學生資助工作的首要步驟，只有準確分類和精準認定，才能為學生提供針對性較強的經濟方面的資助。高校貧困生認定工作每學年進行一次，每學期調整一次，相對于老生而言，新生輔導員對學生的家庭經濟情況了解時間較短，如何進行精準認定，成為高校資助工作的一大難題。其次，我國高校在開展認定工作時普遍存在受主觀影響較大、測評標準不明確、判定方法合理性不足等問題。因此，高校貧困生認定模型在理論研究和實際工作兩個層面上都具有十分重要的現實意義。

貧困生認定可視作一個分類問題。為了科學準確地對高校貧困生進行等級認定，許多資助工作者和相關研究人員基于不同的指標進行貧困生認定研究。在認定方法上從傳統的分類方法逐漸向機器學習方法轉變。傳統的方法包括層次分析、決策樹、聚類、Logistic、SVM等，早在2010年劉善槐［1］就利用教育支出、健康狀況、平均收入和生源類別四個因素建立了Logistic回歸模型，實現了貧困生的二分類，即是否為貧困；2018年劉嘉慶［2］利用一卡通消費數據來預測學生的困難等級；2019年陳瑞虹［3］建立基于SVM算法的高校貧困生等級識別模型。近年來，機器學習在分類問題上得到了廣泛應用，具有代表性的是神經網絡和集成學習算法。程茜宇［4］以某高校資助工作為例，利用深度神經網絡方法構建了學生資助評定模型，認定準確率與傳統算法相比得到一定提升。

深度神經網絡的發展在機器學習領域取得了顯著進展，往往在訓練過程中存在調參困難、訓練時間長和樣本需求量大等缺點，于是越來越多的學者將目光投向集成學習算法，如隨機森 林（Random Forest，RF）［5］、XGboost（eXtreme Gradient Boosting）［6］以 及 梯 度 提 升 樹（Gradient Boosting Decision Tree，GBDT）［7］等。2017 年，唐燕［8］提出將隨機森林算法應用于高校貧困生認定中，并驗證了其準確率高于決策樹算法。楊勝志［9］利用反映學生在校行為數據，包括消費情況、表現情況和學習情況，通過改進后的GBDT模型實現貧困生的四分類，得到的準確率并不理想。2019年陸桂明［10］應用XGBoost模型對貧困生進行分類預測，得到的準確率為53.68%，相比Logistic和SVM兩種方法取得更好的分類效果。

深度森林（DeepForest，DF）［11］是基于決策樹構建的深度集成模型，在高光譜圖像分類［12］、信用評估［13］、交通風險等級［14］等問題上取得了顯著的效果。本文以我校貧困生數據為例，從生源類別、固定資產、經濟狀況、特殊群體、人力資源和突發狀況六個方面，提出了ADA-MDF貧困生認定模型。該模型引入ADASYN算法有效改善了數據的不平衡性，并改進了深度森林的級聯結構，實驗結果與我校目前使用的“本科生困難程度測評模型”相比，準確率提高了8.81%，能夠對貧困生認定起到積極的指導作用。

1 相關理論

1.1 深度森林算法

2017年，周志華提出了多粒度級聯森林方法，構建了深度森林模型。這是一種非神經網絡類型的深度模型，這一模型表現出較強的表征能力，與深度神經網絡模型相比，超參數更少、分類效率更高，具有更優異的分類性能。

如圖1所示，深度森林主要由兩個部分構成：多粒度掃描（Multi-grained Scanning）和級聯森林結構（Cascade Forest Structure）。在多粒度掃描中，滑動窗口用于掃描原始特征，假設原始輸入特征為p，滑動窗口大小為wi，則每個窗口都會產生p-wi+1個特征向量。當分類個數為n時，每個森林產生n(p-wi+1)個類向量，記為m。從而計算出每個樣本對應類別的概率，將這些森林生成的概率向量拼接成新的特征向量，用作級聯森林結構的輸入。

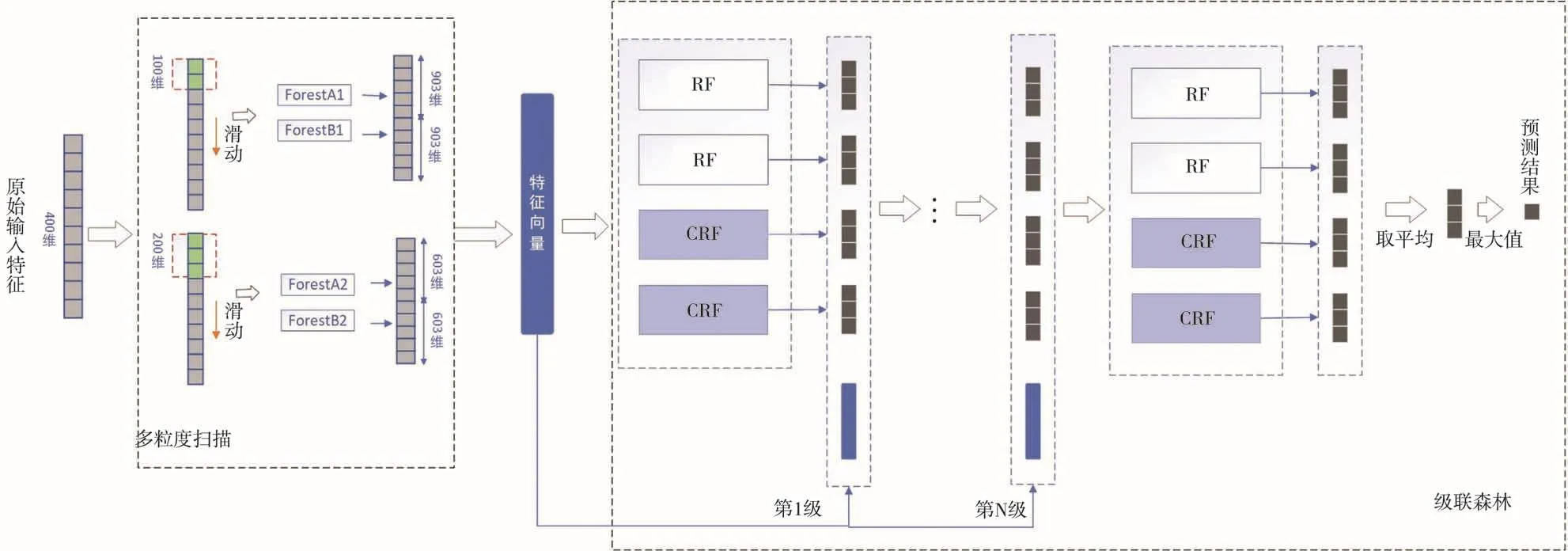
圖1 深度森林框架

級聯森林結構的每層都是由兩個RF和兩個完全隨機森林（Completely Random Forest，CRF）組成。每個CRF包含m棵完全隨機樹［15］，通過在每個節點上隨機分配一個用于分裂的特征，并生長一棵樹直到純葉，即每個葉節點僅包含同一類樣本；每個RF包含m棵樹，每個節點隨機選擇個候選特征（d是輸入特征的數量），然后選擇Gini值最佳的特征進行分割。每個森林通過計算相應葉節點上不同類別的訓練樣本的百分比來估計類的分布，并對同一森林中的所有樹求平均值，得到每個森林的一個類向量，共得到4n維的特征向量（n分類，4個森林），與原始特征向量連接，即4n+m維的特征向量，共同輸入到下一級。在最后一級，取所有向量的平均值作為最終的類向量，概率最高的類為該樣本的最終預測類別。每個森林產生的類向量可以通過k倍交叉驗證來生成，以降低過度擬合的風險。如果驗證集沒有顯著的性能提升，則訓練過程自動終止。

1.2 ADASYN算法

自適應綜合過采樣（Adaptive Synthetic Sampling，ADASYN）［16］最大的特點是考慮了數據的分布密度，使合成的新樣本更加地貼近原始數據，不會破壞原有數據集的分布空間。具體流程如下：

設訓練數據集S={xi,yi},i=1,...,m。其中，xi是p維特征空間中一個樣本，yi∈Y ={1,-1}，ms和ml分別為少數類和多數類樣本，有ms≤ml且ms+ml=m。

（1）計算不平衡度：

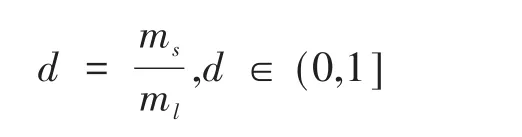
（2）計算需要合成樣本數量：

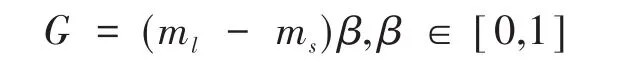
（3）利用歐式距離計算xi的k個最鄰近樣本，統計k個鄰近中屬于多數類的樣本個數Δi，計算：

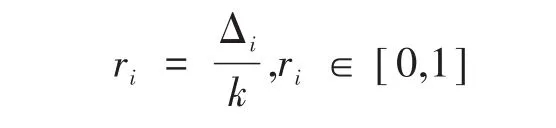
（4）正則化ri，得到密度分布：

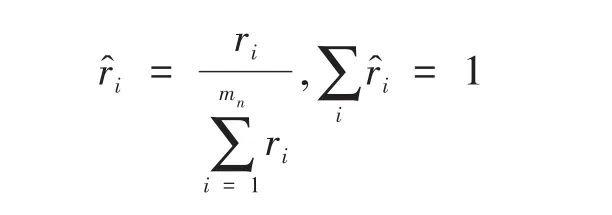
（5）對每個少數類樣本計算合成樣本的數目：

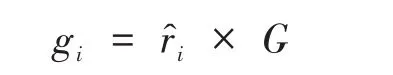
（6）利用k鄰近算法隨機選擇xi附近的一個樣本xj，生成新樣本：

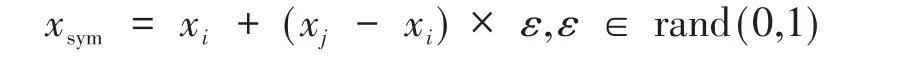
重復合成，直到滿足步驟（5）需要合成的數目為止。

1.3 ADA-MDF貧困生認定模型

原始深度森林的級聯結構由RF和CRF組成，這兩種分類器都是集成學習中Bagging思想的典型代表。誤差-分歧分解（Error-ambiguity decomposition）理論［17］指出“各學習器的準確性越高，多樣性越大，集成的效果就越好”。針對貧困生數據特征復雜多樣問題，本文對其級聯結構的多樣性進行優化，引入Boosting算法和機器學習中的線性分類器，增強學習器的多樣性。最終選取 RF、CRF、XGboost、Logistic和隨機梯度下降法（Stochastic Gradient Descent，SGD）五種分類器構建全新的級聯結構，如圖2所示，其中Logistic、SGD為線性模型，有學習能力強、收斂速度快等特點；RF、CRF和XGBoost屬于非線性模型，具有很好的擬合效果。訓練時，各分類器在特征空間上可以發揮各自優勢以充分學習多特征的信息，對多粒度掃描階段生成的特征向量進行深度迭代，從而更加精準地預測每條訓練集數據所屬的類別，進一步增強了模型的集成能力和泛化能力。本文是針對貧困生等級的三分類研究，每個弱學習器都會生成一個長度為3的概率向量，每一級共產生15個增強特征向量，再與多粒度掃描階段生成的特征向量拼接，輸入到下一級，優化后的深度森林模型稱為MDF模型。

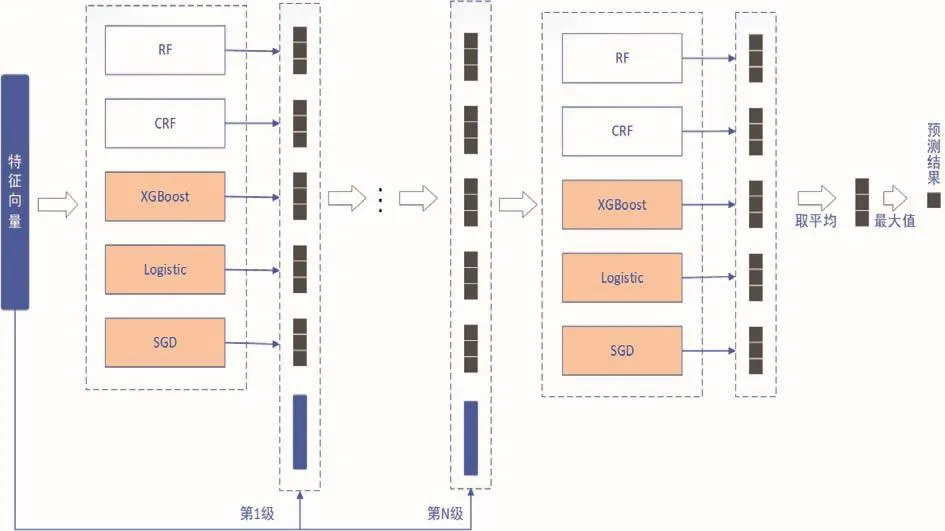
圖2 改進的級聯森林結構

深度森林算法中缺少對類別不平衡數據均衡化的設計，訓練樣本過少，會導致學習不充分，難以保證模型的精度，因此把ADASYN算法融入到MDF模型中，構建ADA-MDF貧困生認定模型，通過過采樣增加少數類樣本量，有效解決不平衡數據下貧困生的認定問題。模型的具體框架如圖3所示，首先對原始數據進行預處理后，按照8∶2的比例劃分訓練集和測試集，實驗針對訓練集進行ADASYN過采樣，將過采樣后的數據輸入改進后的MDF模型，取5倍交叉驗證后的平均值，如果近兩層內性能沒有增長，訓練過程停止，保存模型；最后輸入測試集，預測貧困生等級，輸出實驗結果并計算準確率。

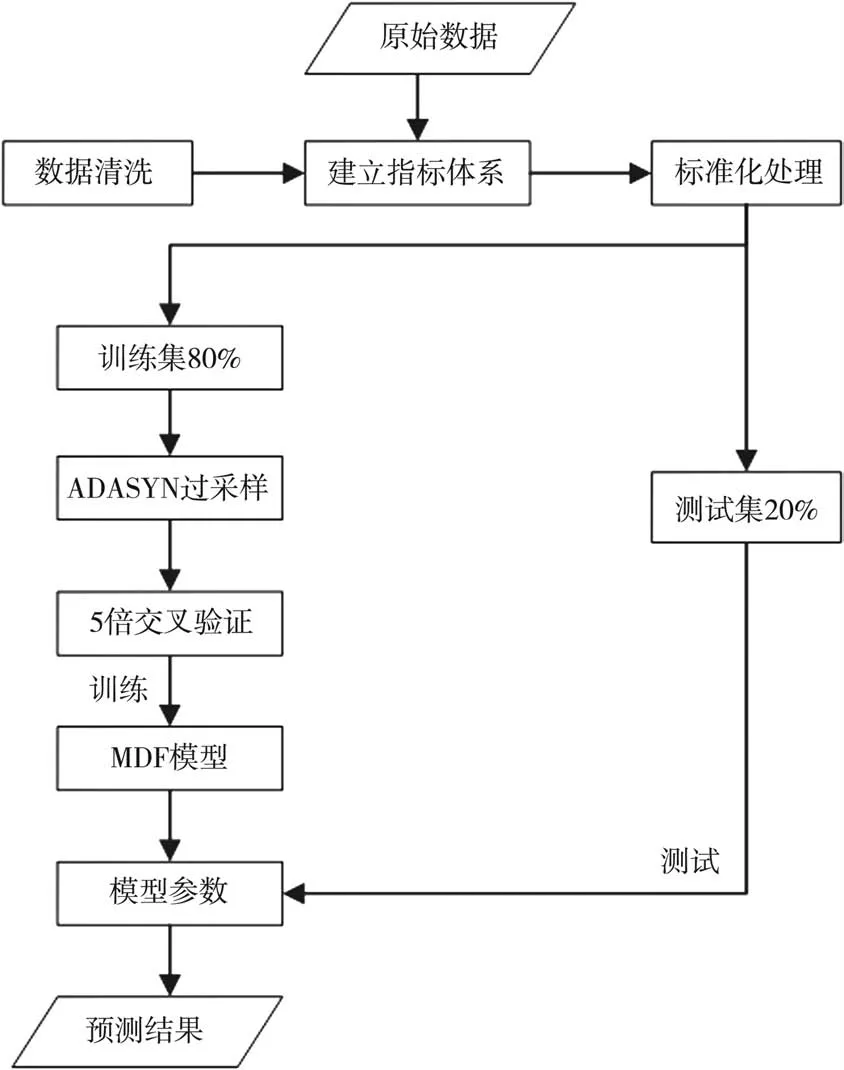
圖3 ADA-MDF貧困生認定模型

2 實證分析

2.1 數據采集和處理

本文獲取到我校2017-2020年申請貧困認定的學生數據，進行匯總清洗后得到3 700條數據。其中，1 196人為特別困難，1 943人為一般困難，561人為不困難，三個等級分別用“2”“1”“0”表示。這里可以看出原始數據存在一定不平衡性，不困難類別的樣本量非常小，會對準確率造成影響。

在對已有研究進行總結的基礎上，結合教育部最新政策要求，本文將建檔立卡等特殊困難群體因素考慮在內，從6個評價因素共25個具體屬性提出高校貧困生評價指標體系，如表1所示。

表1 貧困生評價指標體系

根據評價指標的定義，對“生源類別”“是否貸款”“擁有住房”“住房類型”“低保”“建檔立卡 ”“ 殘 疾 ”“ 單 親 ”“ 孤 兒 ”“ 外 債 金 額 ”“ 家 庭 年 總純收入”“家庭月生活費”“自己月均生活費”“父親狀況”“母親狀況”“家庭自然災害”“家中有大病患者”“家用電器”“交通工具”“收入來源”共20個指標，按照困難程度逐漸加深的順序一一對應轉化為數值數據0～7；剩余“就讀幼兒園人數”“初中小學人數”“高中及中專人數”“就讀大學人數”“贍養老人人數”5個指標為計量數據，故沒有進行轉化。

完成數值轉化后，在ADA-MDF模型分析貧困生數據的過程中，對25個指標進行歸一化處理，把特征數據映射到［0，1］之間。這里采用最小-最大歸一化方法，公式如下：［18］

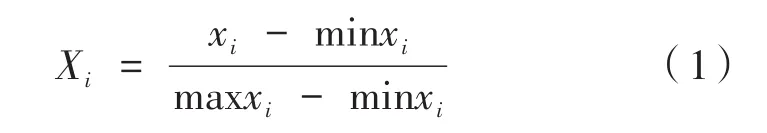
其中，xi代表第i個指標；minxi、maxxi分別代表xi的最小值與最大值；Xi表示轉化后的數值。對各個指標貧困數據進行歸一化處理后，每個學生簡化成一個貧困向量，25個元素分別代表相關指標的值，定義如下：

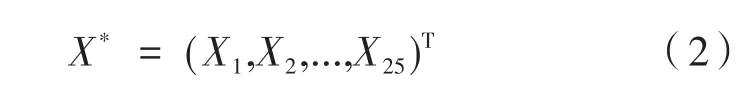
2.2 模型評價指標

本文研究的貧困生等級認定是一個三分類的問題，給出三分類的混淆矩陣，如表2所示。通過計算精準率（P）、準確率（ACC）、召回率（R）、F1值和macro-F1值來評估模型的性能，定義1給出了以上指標的計算公式。

表2 貧困生等級混淆矩陣

定義1：根據二分類中模型評價指標的含義，給出本文中三分類模型使用的評價指標如下：

2.3 實驗結果及對比分析

實驗以8∶2的比例將數據集劃分為訓練集和測試集，在訓練集上進行ADASYN過采樣后得到各類別的樣本量，如表3所示。

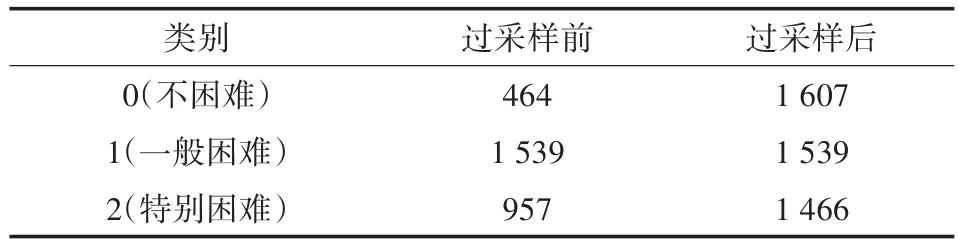
表3 訓練集中各類別的樣本量（單位/個）

對采樣后的訓練集運用5倍交叉驗證，將訓練集劃分成五個不相交的子集，其中四個子集用來訓練，另一個子集用作驗證，這個過程重復五次，則每個子集都被精確地用作驗證集，對每個驗證集的準確率計算平均值。實驗得到ADA-MDF模型最好的層索引為第2層，此時得到的實驗結果如表4所示。

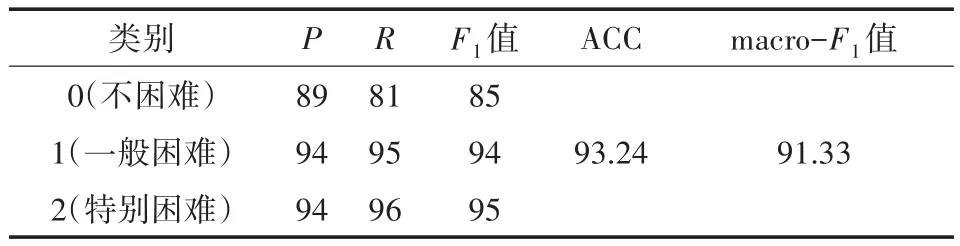
表4 ADA-MDF模型的實驗結果（單位/%）

ADA-MDF模型預測的特別困難、一般困難和不困難的精準率分別為94%、94%和89%。其中，不困難類別的精準率最低，由于該類別樣本數量特別少，造成嚴重的數據不平衡，即使通過ADASYN采樣方法進行補救，但是依然無法達到與其他兩類相同的效果。此外，召回率和F1值也有同樣的表現。相比較之下，特別困難和一般困難的精準率、召回率及F1值均能達到90%以上，特別困難的召回率最高，故該模型在貧困生分類方面具有一定的有效性，預測結果可以為貧困生認定工作提供可信的依據。

圖4為ADA-MDF模型三分類的ROC曲線圖，其中橫軸為“假正率”（False Positive Rate，簡稱 FPR），縱軸表示“真正率”（True Positive Rate，簡稱TPR），見定義2。當i=1時，TPR1表示實際等級為“一般困難”的樣本中被預測為“一般困難”的占比，TPR越大越好；FPR1表示實際等級為“特別困難”和“不困難”的樣本中被預測成“一般困難”的占比，FPR越小越好。由圖可以看出特別困難的曲線面積最大，為98%，一般困難、不困難的曲線面積分別為96%、97%，說明模型的準確度較高，達到較好的分類效果。

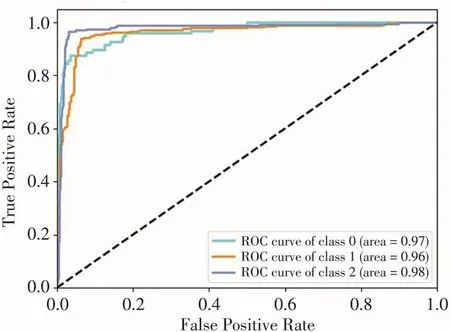
圖4 ADA-MDF模型的ROC曲線圖

定義2：根據二分類中ROC曲線圖的TPR和FPR值，給出本文三分類的TPR和FPR值如下：

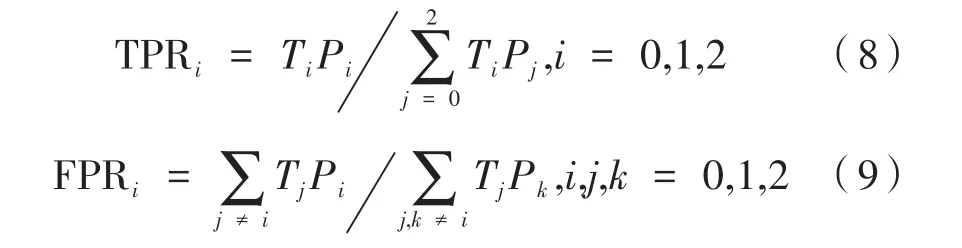
為了進一步研究ADA-MDF模型的性能，分別與圖5中顯示的其他基于樹的模型進行對比，包括 DF、RF、LGB、XGBoost、GBDT 五種分類方法，由于每次實驗都是對原始數據隨機劃分訓練集和測試集，一次實驗并不具備說服力，為了產生公平的比較，每種方法均采用默認的參數，分別進行了10次實驗，圖5（a）記錄了十次實驗的準確率，可以看出，ADA-MDF基本保持在中上游，且準確率最高達到93.38%，其中ADA-MDF、LGB和GBDT三種模型的極差最小為0.54%，說明這三個模型的穩定性較好。

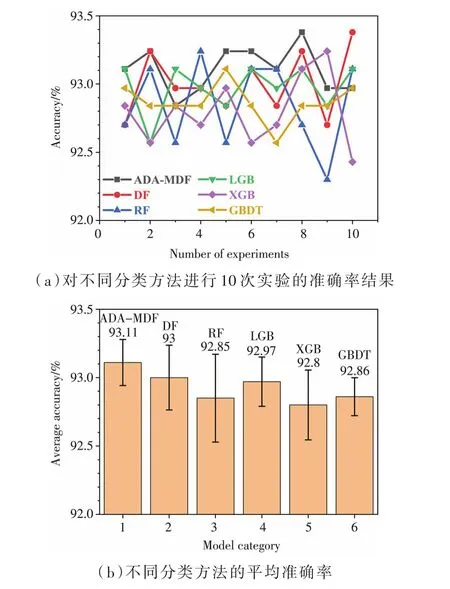
圖5 不同分類方法的實驗結果

圖5（b）為10次實驗的平均準確率，本文提出的ADA-MDF模型平均準確率最高，達到了93.11%，優于其他模型，與平均準確率第二高的DF相比，準確率增長了0.11%，說明改進級聯結構的深度森林有助于提高分類準確率且穩定性更強。從誤差棒的長短可見，ADA-MDF的誤差略大于GBDT模型，但是比其余4個模型小的多，雖然GBDT模型在穩定性和誤差方面具有一定優勢，但是其準確率遠遠沒有達到預期效果，綜上，ADA-MDF模型的綜合性能更為優越。

3 結論

根據貧困生認定工作流程，我校目前使用“本科生困難程度測評模型”的測評結果作為最終認定結果的參考依據，而實際認定過程中會存在等級調整的情況，經計算，測評結果的準確率為84.30%。本文將ADASYN自適應過采樣方法引入到深度森林算法，提高了模型在不平衡數據中的分類效果；創建了一個新的級聯結構，由 RF、CRF、XGboost、SGD、Logistic五種基分類器組成，對特征進行深度學習，實現貧困生的三分類，平均準確率達到93.11%。故本文提出的ADA-MDF模型有助于貧困生等級精準分類，下一步可研究如何進行特征選擇，構建更適用于我校學生的評價指標體系，不斷提高貧困生認定模型的準確率及普適性，貫徹落實精準資助。