一種基于RBM的滾動軸承退化指標構建方法

程道來，魏婷婷，潘玉娜，馬向華

(1.上海應用技術大學 城市建設與安全工程學院，上海 201418；2.上海應用技術大學 機械工程學院，上海 201418；3.上海應用技術大學 軌道交通學院，上海 201418；4.上海應用技術大學 電氣與電子工程學院，上海 201418)

滾動軸承作為旋轉機械中常用部件之一，對其振動信號進行監測與報警，可以有效降低機械維護成本，避免造成意外損失[1]。對滾動軸承做出正確的狀態監測是對其做出預診斷和維修決策的基礎[2]。但由于軸承工作環境的影響，其振動信號往往是非線性和非平穩的，且存在各種噪聲的干擾等[3]，使得利用軸承振動信號對其進行精確的性能退化評估并不簡單。而性能退化評估中的關鍵之處則在于退化指標構建的質量[4]。

近年來，為了精確評價軸承性能退化過程，出現了大量的退化指標構建技術。退化指標的構建可分為物理退化指標和虛擬退化指標兩大類[5]。物理退化指標與設備失效物理特性有關，一般采用統計方法或信號處理方法從監測信號中提取[6]，常見的有時、頻域統計指標[7-8]。復雜度指標如：張龍等提出包絡譜譜峰因子(crest of envelope spectrum，EC)作為復平移Morlet小波濾波器的中心頻率和帶寬參數選擇的依據，再將經過濾波信號的RMS值與EC值的乘積作為軸承故障程度評估指標；Liu等[9]利用改進的集成經驗模態分解(ensemble empirical mode decomposition，EEMD)構建健康指標，對滾動軸承性能退化過程做出了準確評估。但單一指標會存有只能在特定的故障和操作條件下才能獲得較好的評估結果的問題。

對于虛擬退化指標，它是通過融合多個物理退化指標或多傳感器信號來構建的，通常這種方式構建的退化指標沒有明顯的物理意義，只是虛擬地描述了軸承的退化趨勢。潘玉娜等[10]對軸承振動信號進行小波包分解，以其節點能量作為退化特征，選擇支持向量數據描述(support vector data description，SVDD)做評估模型完成軸承退化指標的構建。Zhang等[11]提取出退化特征后，使用基于馬氏距離(Mahalanobis distance，MD)的評估方法融合多個特征后描述軸承健康狀態。Wang等[12]利用希爾伯特變換與魯棒局部均值分解相結合的原始信號去噪和時頻域特征提取，再使用隱馬爾科夫(Hidden Markov model，HMM)模型建立軸承的退化指標。Rai等[13]提取出正常狀態下軸承振動信號的時域和頻域特征用來訓練自組織映射網絡(self-organizing map，SOM)，并定義測試數據輸入SOM中得到的最小量化誤差作為健康指標。周建民等[14]采用時域方法和集成經驗模態分解的能量熵提取軸承特征，經過挑選后得到最終的退化特征，而定義軸承性能退化指標是用三種不同故障程度的軸承數據訓練(support vector machine，SVM)模型，將軸承全壽命周期數據輸入模型后，得到軸承性能退化曲線。但以上方法退化特征主要基于人工提取，構建的退化指標高度依賴先驗知識，且有的方法中構建退化指標的模型需要故障數據，忽略了設備實際運行中難以獲取故障狀態下數據的問題。

深度學習在滾動軸承故障分類診斷上應用頗為廣泛[15-18]，其強大的自學習能力擺脫了在信號處理中對人工經驗的依賴，基于監督學習的軸承故障分類診斷需要標記不同類型的故障數據訓練模型，而軸承的性能退化過程是循序漸進的變化，將其簡單的歸為故障分類診斷并不合適，有學者嘗試將無監督深度學習方法應用在軸承退化指標構建上。如Pan等[19]利用正常狀態下的軸承數據建立深度自編碼模型(deep auto-encoder，DAE)，然后通過對輸入數據進行編碼和解碼，利用重構數據與輸入數據之間的均方根誤差來評價軸承的健康狀態。受限玻爾茲曼機(restricted Boltzmann machine，RBM)作為無監督學習的模型之一，能夠通過調整模型的參數使得模型的概率分布盡可能地符合訓練數據的真實分布，同時也能達到降維和特征提取的作用。

基于以上分析，本文提出一種基于RBM的退化指標構建方法。該方法以滾動軸承正常狀態下歸一化的幅值譜作為RBM模型的訓練樣本，模型訓練完成后，將其輸出作為退化指標構建的基礎。通過不同情境下的滾動軸承全壽命周期試驗數據驗證了該方法可以很好的揭示軸承退化規律。

1 理論介紹

1.1 幅值譜

幅值譜獲得方式即對采樣所得的時域信號進行快速傅里葉變換(fast Fourier transform，FFT)，求得關于該時域信號的頻率構成信息，其數學表達式為

(1)

式中，x(t)為時域信號。對于時域離散信號有

(2)

1.2 受限玻爾茲曼機

受限玻爾茲曼機是由多倫多大學的Salakhutdinov等[20]提出的，其作為一種特殊的馬爾可夫隨機場，可以在觀測數據和隱藏特征之間建立聯合分布。RBM主要由用于輸入數據的可見層v和提取特征的隱含層h組成，其結構如圖1所示。

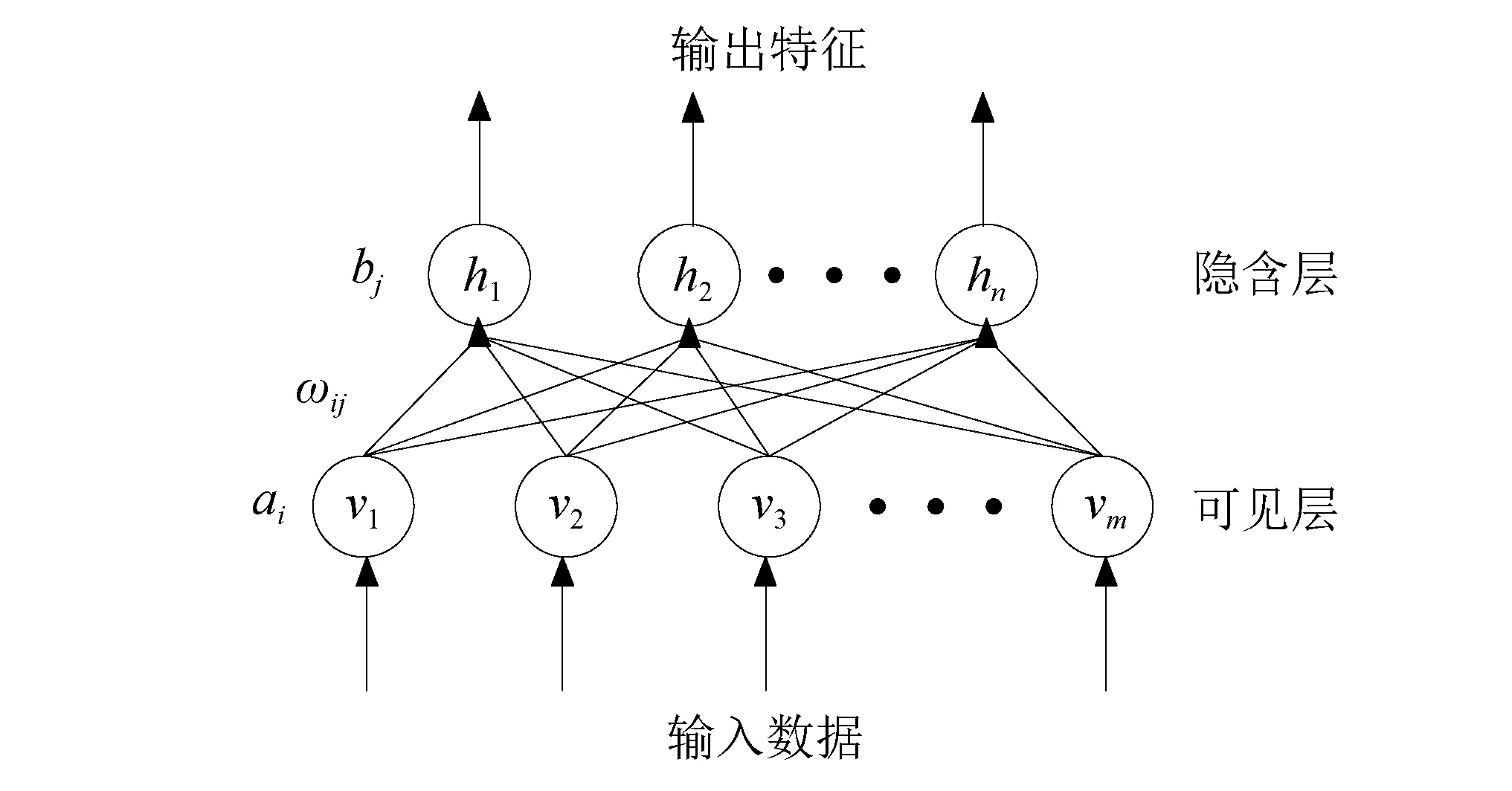
圖1 受限玻爾茲曼機結構簡圖Fig.1 Structure schematic of RBM

可視層v和隱含層h中分別包含幾個獨立不相互連接的神經元，但層與層之間是完全連接的。受限玻爾茲曼機是一個基于能量的模型，假設圖1所示的RBM中，可視層v有m個可見單元，隱含層h有n個隱含單元，ai和bj分別表示可視層vi和隱含層hj的偏置項，ωij是可視化層第i個單元和隱含層中第j個單元之間的連接權重，對于上述網絡，給定一組狀態(v,h)，則可自定義其能量函數

(3)

RBM里用來描述訓練樣本的分布，引入了屬于熱力學統計物理的相關概念即正則分布，是物理學家用來描述一個不知所處狀態的概率的函數[21]

(4)

式中：Pθ為系統處于狀態的概率；Eθ系統處于狀態θ時的能量；Zθ為歸一化因子。處于該狀態的能量越小，則屬于該狀態分布的概率越大，系統也就越穩定。

將式(3)代入式(4)可得狀態(v,h)的聯合概率分布為

(5)

對應其聯合概率密度分布的邊緣分布即觀測數據v的概率分布表達式為

(6)

通過訓練得到模型參數ωij，ai，bj后，由于RBM層間有連接，層內無連接，且層內單元的激活值為零一分布的特殊結構，可以通過計算可見層和隱含層中單元激活的條件概率分布確定Pθ(v)[22]，其中隱含層h中第s個單元節點激活的概率為

(7)

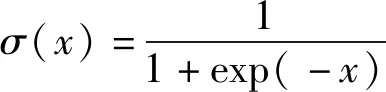
推導過程如下：

為方便推導過程，首先記h-s表示在h中挖掉分量hs后得到的向量；

h-s=(h1,h2,…,hs-1,hs+1,…,hn)T

(8)

并記

(9)

和

(10)

則有

Eθ(v,h)=-Q(v,h-s)-Os(v)

(11)

對Pθ(hs=1|v)的推導有

Pθ(hs=1|v)=Pθ(hs=1|h-s,v)=

(12)

當給定隱含層單元的狀態時，由于各可見單元的激活狀態之間是條件獨立的，則第s個可見單元節點的激活概率為

(13)

訓練數據輸入到RBM中，相關參數ωij，ai，bj按照一定的更新準則改變，該準則是由Hinton等[23]提出的基于Gibbs采樣的k步對比散度(contrastive divergence，CD-k)算法，該算法已成為訓練RBM的標準算法，更新準則為

(14)

ai=ai+η[P(hj=1|v)-P(hj=1|vk)]

(15)

(16)

式中：k為采樣步數，默認取值為1；η為學習率。

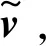
(17)

式中：d為訓練樣本輸入時的批次大小，m為訓練樣本的長度即圖1中可見層單元數；err為平均每個樣本下每個點的重構誤差。向訓練完成的RBM模型輸入測試樣本hc，則其輸出為隱含層節點為1的激活概率，可認為是測試數據屬于訓練數據分布的概率P，由式(7)可得

(18)

又因單元節點為零一分布，則可認為其隱含層節點為0的概率是測試數據不屬于訓練數據分布的概率，大小即為1-P。

2 退化指標的構建

基于RBM的理論特點，本文提出了一種基于RBM的滾動軸承性能退化指標構建方法，其特點為隱含層單元數設置為一個，基于該方法的滾動軸承性能退化評估模型如圖2所示。其具體步驟為：

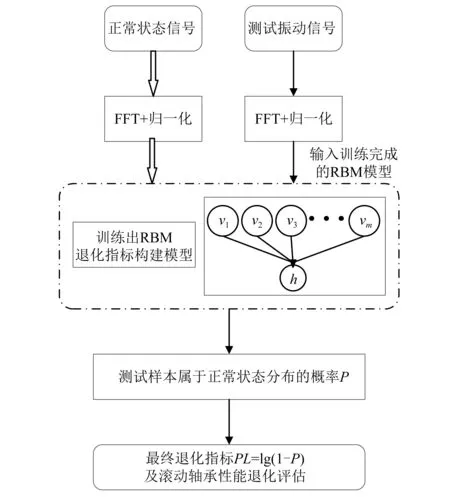
圖2 基于RBM的退化指標構建方法流程Fig.2 Flow chart of degradation index construction method based on RBM

步驟1收集滾動軸承正常狀態下的振動信號，經過FFT處理后再進行歸一化；

步驟2將步驟1處理后的滾動軸承正常狀態下的數據作為訓練樣本，建立RBM退化指標構建模型；

步驟3對于測試的滾動軸承全壽命周期振動信號，將經過步驟1處理得到的樣本，再依次經過步驟2中已經訓練完成的RBM退化指標構建模型，可求得測試樣本屬于軸承正常狀態分布的概率P；

步驟4以步驟3中得到的概率P為基礎，計算得出最終的退化指標PL，計算公式為

PL=lg(1-P)

(19)

其中PL的意義即對測試樣本不屬于軸承正常狀態分布的概率做以十為底的對數計算，以此增加退化指標對軸承整個退化過程區分的敏感性。

3 試驗驗證

3.1 試驗數據介紹

采用了文獻[24]中試驗所得的滾動軸承全壽命周期試驗數據，其中軸承型號為6307，轉速為3 000 r/min，徑向載荷1.113 kg，采樣頻率為25.6 kHz，采用加速度傳感器每隔1 min采集一組長度為20 480的數據，數據采集從軸承正常狀態一直持續到壽命結束，共采集了1 062組數據，最終失效形式均為內圈嚴重點蝕，將此組數據記為B1。

另外，為了驗證本文所提方法應用在不同情境下的滾動軸承也能實現較好的退化評估，同時選擇了源于美國辛辛那提大學公布的滾動軸承振動測試的全壽命周期數據[25]進行試驗驗證，該試驗臺中有4個施加了27 00 kg徑向載荷的型號為ZA-2115的軸承，在運行了163 h后一軸承外圈出現嚴重剝落故障直至失效，軸承振動信號每隔10 min采集一次，采樣頻率20 kHz，共采集到984組樣本，每個樣本包含20 480個數據點，將此組數據記為B2。

3.2 基于RBM的退化指標評估結果

對B1和B2兩組滾動軸承數據做基于RBM的退化指標PL的構建。其中，RBM可見層和隱含層神經單元個數分別設置為1 024和1；訓練批次設置為100；學習率設置為0.01；訓練樣本兩組均選擇了前300個正常樣本。訓練時的兩組模型重構誤差隨迭代次數變化如圖3所示，隨著迭代次數的增加逐漸降低并且收斂，在誤差趨于穩定時即該模型訓練完成。為增加訓練速度，訓練時迭代次數設置為50。

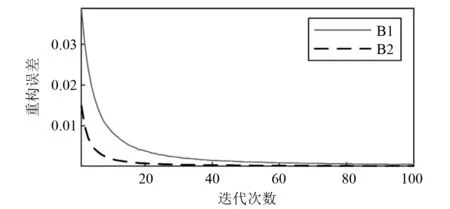
圖3 重構誤差隨迭代次數變化Fig.3 The reconstruction error varies with the number of iterations

首先對B1進行分析，其全壽命周期退化指標PL如圖4所示。0～513 min期間PL基本保持穩定，說明此階段的滾動軸承處于正常工作狀態；從513 min開始PL值出現小幅上升，之后保持穩定，可認為此時軸承進入了早期微弱故障狀態；在978～1 039 min期間的樣本PL值斷崖式上升且保持穩定，說明此階段軸承屬于故障加劇狀態；1 039 min后的PL值波動較大且變化毫無規律，反映出軸承此刻進入失效狀態。

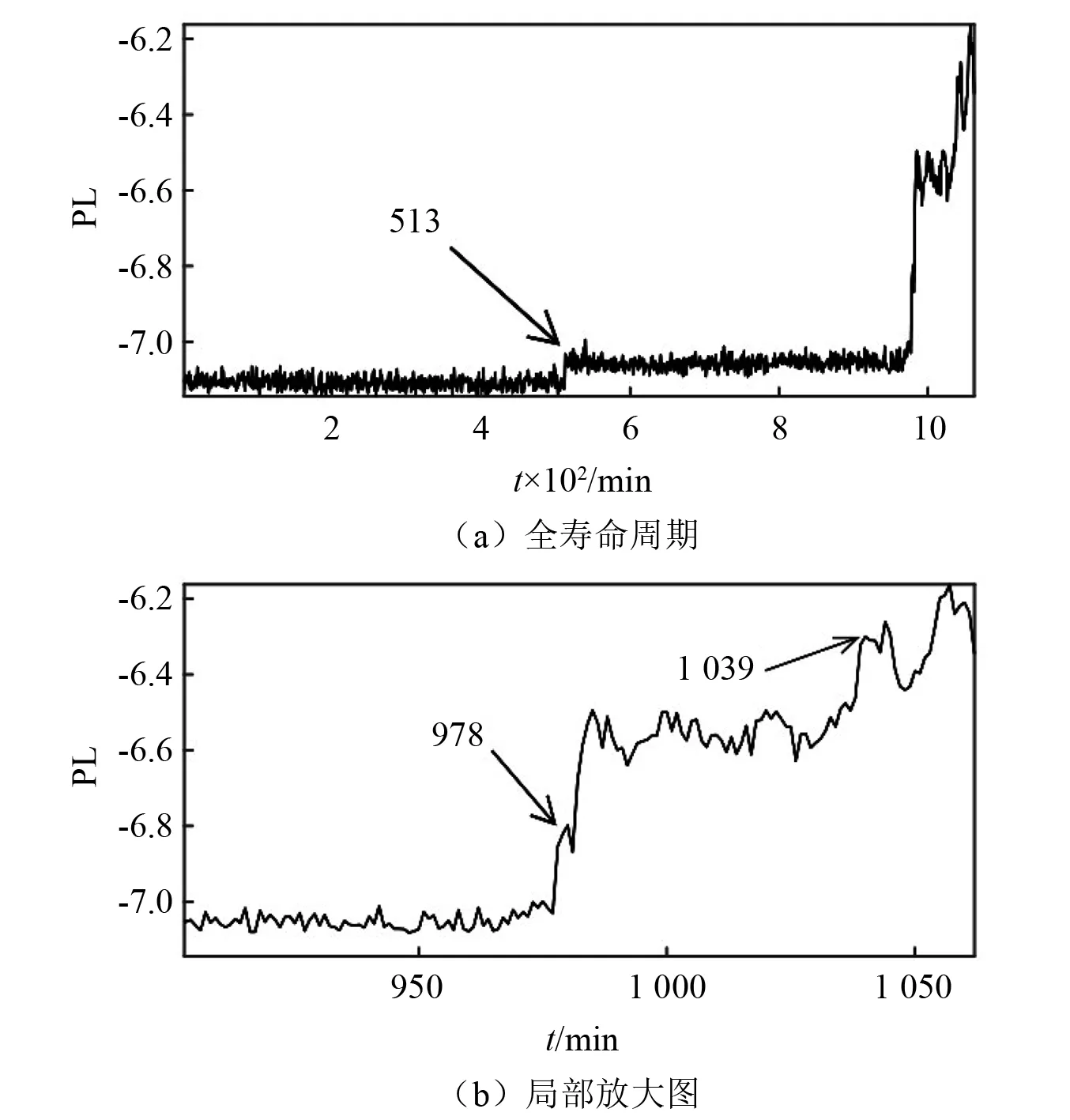
圖4 B1全壽命周期PL退化指標Fig.4 Full life cycle PL degradation index of B1

然后對B2進行分析，其全壽命周期下的退化指標PL如圖5所示。在滾動軸承運行的0～5 340 min期間，樣本的PL值較為穩定，說明其運行屬于正常狀態；在5 340～7 030 min期間的PL值逐漸上升，可認為軸承從5 340 min出開始出現早期微弱故障，且隨著時間的變化，早期微弱故障的特征越明顯；在運行的7 030 min～9 710 min期間，樣本的PL值再次上升并伴隨小幅波動，說明此時段的軸承運行屬于故障加劇狀態；從9 710 min開始的PL值波動較大且毫無規律，說明該期間的軸承已經失效。

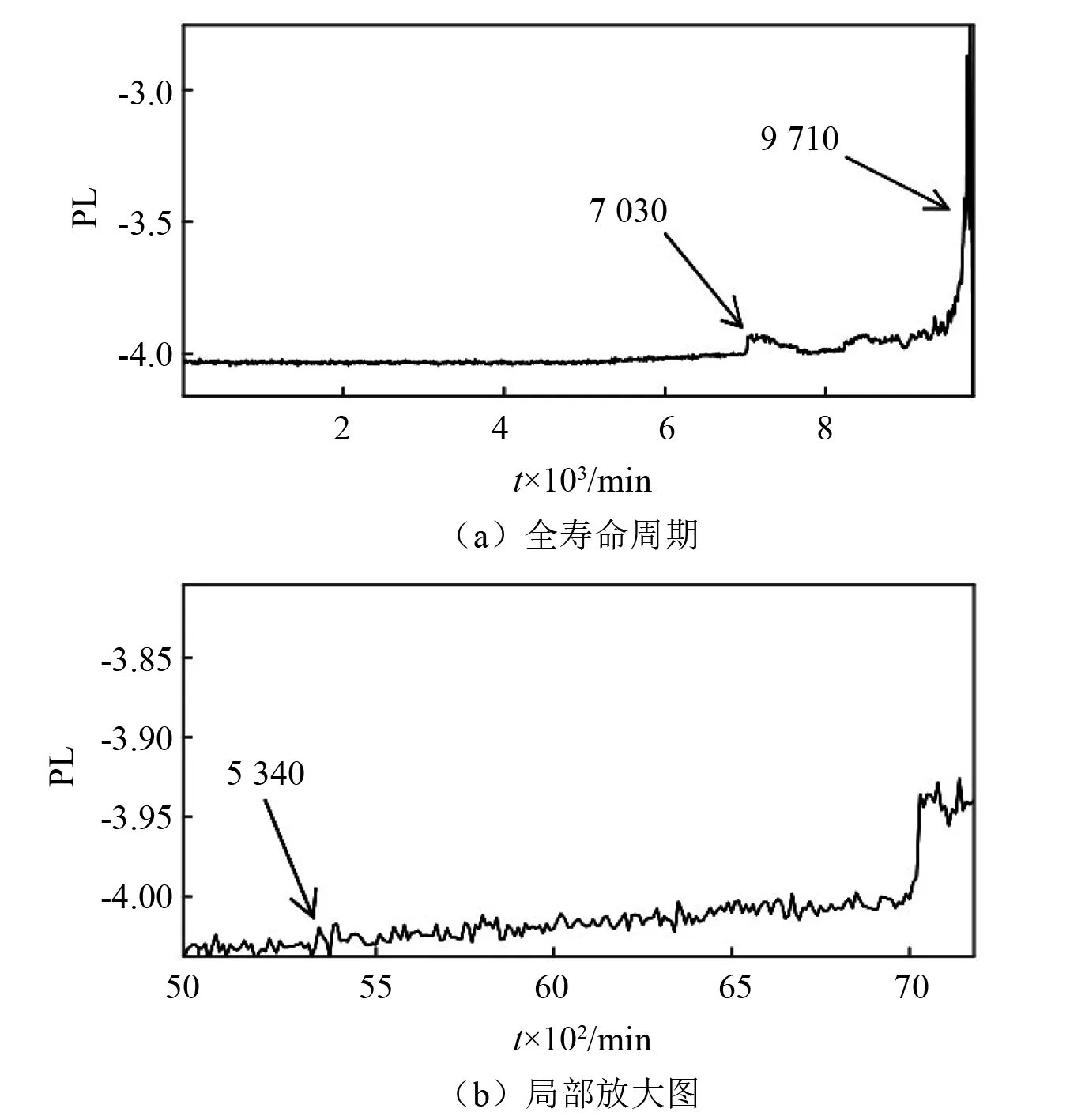
圖5 B2全壽命周期PL退化指標Fig.5 Full life cycle PL degradation index of B2

3.3 結果對比分析

本文所提指標對B1退化評估的變化趨勢與文獻[26]中的相一致，驗證了本文方法的有效性。對B2的退化評估分別與文獻[27]和文獻[28]所提方法做出的結果相比，其中兩篇文獻分別構建的是物理退化指標和虛擬退化指標，且主要是針對檢測軸承早期微弱故障提出的，對比結果為本文所提方法與上述兩篇文獻中發現早期微弱故障出現的時刻相同，驗證了本文方法具有一定的早期微弱故障檢測能力。另外，張龍等研究中自適應最優頻帶選擇的過程中多處依賴專家經驗知識，如：能得到比較滿意的中心頻率時尋優取值點的確定，帶寬的確定；王斐等中提到其經過大量分析研究才選定VMD奇異值，均方根值，樣本熵值作為SVDD模型的輸入，進而得到較好的軸承性能退化評估，而本文所提方法中的RBM可自動提取出退化指標，無需依賴專家經驗知識以及人工在構建退化指標花費大量時間選擇退化特征。

為了進一步驗證本文所提方法的優越性，使用同是屬于無監督學習的深度自編碼網絡模型對這兩組數據做出性能退化評估，并與本文方法做出的結果進行對比分析。將基于DAE模型提取出的退化指標記為DAE-DI(DAE-degradation index)，對B1組滾動軸承數據做基于DAE的性能退化評估，其全壽命周期的DAE-DI值變化如圖6所示，DAE-DI對B1組數據的性能退化評估單調性較差，無法明確檢測出早期微弱故障出現的時刻，但其對軸承后期的退化過程的評估還是比較準確的。對B2組數據做基于DAE的性能退化評估，其全壽命周期的DAE-DI值變化如圖7所示，DAE-DI對B2組數據的性能退化評估具有一定的單調性，能夠表現出滾動軸承的性能退化的大致趨勢，但所得曲線過于粗糙，淹沒了早期微弱故障剛出現時的特征，同樣無法準確檢測出早期微弱故障出現的時刻。

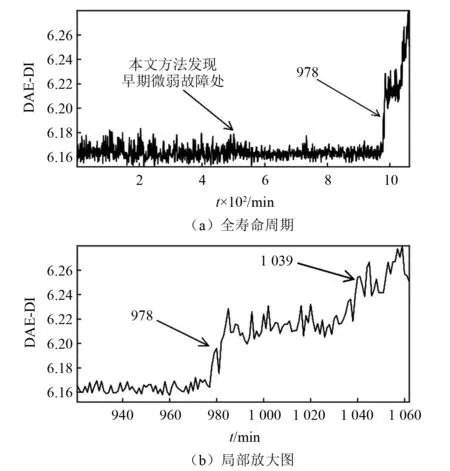
圖6 基于深度自編碼的B1全壽命周期退化指標Fig.6 Full life cycle degradation index of B1 based on DAE

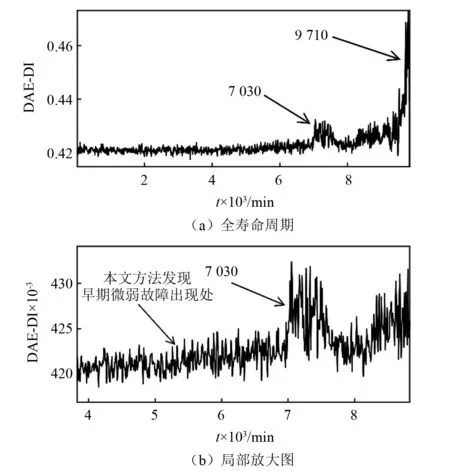
圖7 基于深度自編碼的B2全壽命周期退化指標Fig.7 Full life cycle degradation index of B2 based on DAE

由上述分析可知，基于RBM構建的退化指標應用在不同情境下的滾動軸承都能夠清晰反映出其性能退化的過程，該指標對早期微弱故障也具有一定的敏感性，并且指標構建過程避免了人工先驗知識的參與；另外，相較于同是屬于無監督學習的DAE網絡模型做出的軸承性能退化評估結果，基于RBM構建的退化指標表現更好。

4 結 論

(1)介紹RBM相關理論的同時說明了RBM隱含層單元節點輸出的意義，并提出了一種基于RBM的滾動軸承退化指標構建方法，將其隱含層輸出作為退化指標構建的基礎。

(2)與最近相關文獻相比，基于RBM構建退化指標面對不同情境下的滾動軸承都能夠有效評估出其性能退化過程，準確檢測出滾動軸承早期微弱故障的出現，擺脫了對人工經驗的依賴，且在一定程度上節省了時間與精力。

(3)與同是屬于無監督學習的DAE構建的退化指標相比，基于RBM構建的退化指標表現更佳。

(4)用正常狀態下的數據即可實現該模型的構建，克服實際軸承設備運行中故障樣本較難獲取的問題，對于軸承設備性能監測具有很好的指導意義。