基于Tube的撓性航天器模型預測姿態控制及主動振動控制

管 萍，吳希巖，戈新生

(北京信息科技大學 自動化學院，北京 100192)

現代航天器常帶有太陽帆板、大型天線桁架等大型撓性附件，大型撓性結構會加劇撓性附件振動使得姿態控制問題難于處理。同時，重力梯度、太陽輻射、地球磁場等各種環境干擾力矩不斷影響著航天器的運行過程。并且，隨著航天器的不斷發展，為確保航天器在性能極限下安全可靠地運行，對于航天器在軌大角度姿態機動的控制精度要求也越來越高。所以，撓性航天器的高精度姿態控制以及有效的振動抑制是目前仍在解決的難點問題[1]。

近幾年來，國內外學者們將很多有效的控制方法應用到航天器的姿態控制中，并取得了較好的控制效果。文獻[2]提出了一種自適應模糊PID控制器，使航天器系統具有較好的控制性能。文獻[3]針對撓性航天器進行大角度姿態快速機動中的姿態控制問題，設計了基于期望補償的自適應魯棒姿態控制器。文獻[4]提出一種基于模糊控制原理的改進型自抗擾控制方法，實現了撓性航天器較好的姿態控制。文獻[5]采用自適應魯棒方法設計了姿態控制器，有效地降低了干擾和轉動慣量不確定性對撓性航天器系統性能的影響。文獻[6]針對撓性航天器的姿態快速機動問題，設計了基于終端滑模的有限時間控制律。文獻[7]針對一種帶有撓性附件和液體晃動的深空探測航天器姿態控制問題,提出了自抗擾控制律。然而在實際航天任務中，航天器常會受到如執行器受限、燃料受限、以及躲避禁飛區時姿態角受限等系統的約束限制，上述控制器未考慮實際系統對控制力矩的約束，在實際運行中會影響控制性能[8]。模型預測控制(model predictive control,MPC)通過在線優化求解控制律，在線優化過程中，將各種約束條件進行充分的考慮，從而得到最優的性能指標，并可滿足各種約束條件的控制算法[9]。MPC具有簡單可重構性、層次靈活性等優點，已被廣泛應用于航天控制中。文獻[10]將線性時變模型預測控制應用于欠驅動衛星的姿態控制器設計，使衛星能夠以較高的精度達到期望角度。文獻[11]將線性時變模型預測控制方法應用于磁驅動衛星的姿態控制中，得到了較好的控制效果。然而上述方法均將航天器預測模型進行部分線性化，很難獲得較為滿意的控制效果。當系統的實際模型為非線性時，采用非線性動態模型作為預測模型會更加準確，因此會得到較好的控制性能[12]。文獻[13]將非線性模型預測控制(nolinear model predictive control,NMPC)應用于航天器交會和近距離機動的相對運動控制問題中，快速準確地進行目標控制，然而未考慮航天器存在擾動的情況。文獻[14]針對敏捷小型衛星設計了NMPC控制器，考慮了外部擾動，使姿態角具有較高的控制精度和響應速度。然而此方法未考慮撓性附件對中心剛體的影響，撓性附件振動引起的擾動會影響控制精度。所以在針對撓性航天器進行姿態控制器設計時，需考慮具有強抗干擾能力的控制器。其中，NMPC是有效的控制方法之一。而在具有擾動的情況下，基于Tube的模型預測控制可使被控系統的實際狀態保持在以標稱軌跡為中心的Tube不變集內。因此設計基于Tube的模型預測姿態控制器是處理撓性附件振動引起擾動的有效方法之一。然而文獻[15]僅將所設計的基于Tube的模型預測控制方法應用于二階非線性系統中，其控制系統穩定性的詳細證明及其有限時間收斂性問題還有待于進一步探究。

盡管上述方法可以增強系統的魯棒性同時有效降低包括撓性振動在內的不確定性對系統的影響，但屬于集中控制，僅依靠姿態控制器去抑制撓性附件振動很難得到滿意的效果[16]。因此有必要對撓性振動問題設計主動振動控制器。文獻[17]與文獻[18]分別采用分力合成與輸入成型主動振動控制技術減少了撓性模態振動。然而，分力合成與輸入成形主動振動控制方法均屬于前饋控制方法，系統中存在的干擾會影響控制效果。采用壓電智能材料的閉環反饋主動振動控制方法靈活性高，能夠有效應對外部擾動。其中滑?？刂茖ο到y擾動具有較強的魯棒性和抗干擾能力，可應用于主動振動控制器設計中。然而傳統滑模控制具有切換項和指數趨近律，因此存在著抖振和收斂時間較長的問題。終端滑模與傳統滑模相比具有有限時間收斂、穩態跟蹤誤差小等優點，但仍存在著抖振和奇異性問題[19]。全階滑?？刂茖⒊Ｒ幾兘Y構中的切換項通過微分環節構成新的切換函數，在實現滑動狀態時具有連續性，有效的降低了抖振，且由于控制律中不再包含常規終端滑模中狀態變量的負指數項，所以避免了控制系統的奇異性[20]。因此設計全階滑模主動振動控制器可有效處理撓性附件引起的振動。

本文針對具有控制力矩約束的撓性航天器姿態機動控制這類高階非線性系統，設計了基于Tube的模型預測姿態控制器，給出了詳盡的控制系統穩定性證明，同時還證明了所設計的控制系統可在有限時間內穩定。所設計的Tube-MPC姿態控制器既具有MPC良好的優化能力，又能有效處理擾動對系統的影響，增強系統的魯棒性，使姿態角實現快速跟蹤。在撓性振動抑制方面，設計了全階滑模主動振動控制器，全階滑?？刂撇粌H具有傳統滑?？刂启敯粜詮姡瑓底兓幻舾械葍烖c且無奇異性問題，又能在有效消除抖振的同時使撓性振動模態在有限時間內快速衰減。仿真結果表明，所設計的基于Tube的模型預測姿態控制器和全階滑模主動振動控制器能夠在撓性航天器大角度機動時，使姿態角快速跟蹤期望角度，并且有效抑制了撓性模態振動和外部擾動。

1 撓性航天器的數學模型

以往常用歐拉角和四元數表示航天器的姿態參數，但歐拉角存在大角度奇異問題，四元數雖無奇異性，可存在冗余度，所以本文采用既無奇異性又無冗余度的修正的羅德里格斯參數MRPs(modified rodrigues parameters，MRPs)來表示姿態參數，MRPs定義為

(1)

式中：σ為航天器相對慣性坐標系的MRPs姿態描述，σ=[σ1σ2σ3]T;p為歐拉主軸向量;θ為歐拉旋轉角。

姿態運動學方程為

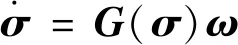
(2)

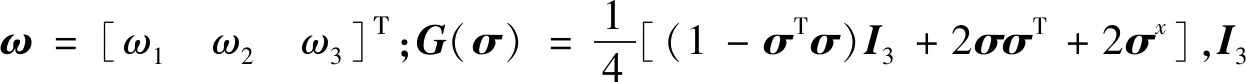
(3)

采用壓電智能材料進行主動振動控制的撓性航天器動力學方程為[21]

(4)

(5)

式中:J為航天器的轉動慣量矩陣;δ∈RN×3為航天器剛體與柔性附件的耦合矩陣;η∈RN×1為柔性附件的模態坐標向量;u∈R3為控制輸入力矩;d∈R3為包括重力梯度、太陽輻射、地球磁場等各種環境干擾力矩;C=2ξΩ為阻尼矩陣;K=Ω2為剛度矩陣;ξ和Ω分別為振動模態的阻尼比和自然頻率;δa∈RN×N為壓電作動器與柔性附件的耦合矩陣;up∈RN×1為壓電作動器的輸入電壓。

將運動學方程(式(2))和動力學方程(式(4))共同構成受擾動的撓性航天器系統為

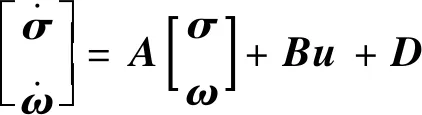
(6)

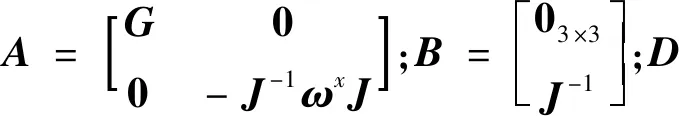
將連續時間的撓性航天器系統(式(6))離散化可表示為

x+=f(x,u)+Dk

(7)

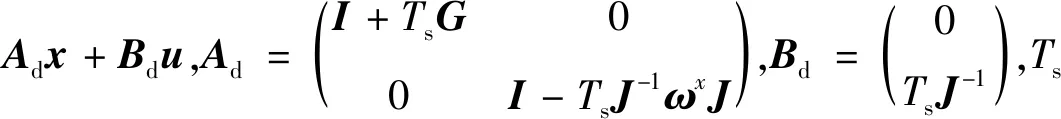
系統所受控制力矩約束

u∈,?{u∈R3×1|-U≤ui≤U,i=1,2,3}(8)

對于系統(式(7))，如不考慮復合擾動Dk，稱為標稱系統

z+=f(z,v)

(9)

式中：z∈?R6×1為標稱系統狀態，為標稱系統所對應的正不變集;z+為z的下一時刻狀態，當系統狀態到達目標狀態z=xd時，f(xd,ud)=xd為系統的平衡點。

標稱系統控制輸入約束為

v∈?

(10)

定義

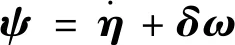
(11)

對式(11)求導，得到

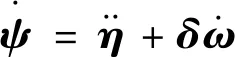
(12)

將式(12)代入式(5)

(13)

將式(13)定義為

(14)

式中：g=-Cψ-Kη+Cδω;h=-δa。

本文的控制目標為：針對撓性航天器(式(6))，設計滿足控制輸入約束的姿態控制器，有效處理擾動對系統的影響，實現姿態角期望指令的快速精確跟蹤；為有效的抑制撓性附件引起的振動，設計主動振動控制器，在有限時間內，使撓性振動衰減到零。

2 基于Tube的模型預測姿態控制器設計

基于Tube的模型預測姿態控制器的主要設計內容為：設計對于原點穩定的標稱軌跡和輔助控制器，使得實際系統的狀態軌跡在有限時間到達所設計的標稱軌跡，并沿著標稱軌跡快速收斂于原點。其中，標稱軌跡由MPC作用下標稱系統狀態從初始狀態到達目標狀態并最終穩定于平衡點產生的；輔助控制器使實際系統狀態處于以標稱軌跡為中心的Tube不變集中，并驅使實際系統從任意初始狀態出發在有限時間內到達標稱軌跡上，從而使實際系統狀態可以沿著標稱軌跡最終收斂至原點。

2.1 標稱軌跡

標稱系統在模型預測控制律作用下從初始狀態到達平衡點產生標稱軌跡，標稱軌跡的優化目標為

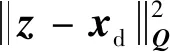
則標稱軌跡的優化問題為

z0(z,xd)={z0(0;z,xd),z0(1;z,xd),…,z0(N;z,xd)}(18)

z*(z,xd)={z0(0;z,xd),z0(1;z,xd),z0(2;z,xd)，

…}?{z0(z,xd),xd,xd，…}

(19)

v*(z,xd)={v0(0;z,xd),v0(1;z,xd),v0(2;z,xd)，

…}?{v0(z,xd),ud,ud,…}

(20)

引理[22]：考慮系統z+=f(z,v)的狀態z∈?Rn，如果存在α1(·)，α2(·)，α3(·)函數，使得連續函數V∶Rn→R+滿足如下條件

V(z)≥α1(|z|)

(21)

V(z)≤α2(z)

(22)

V(z+)-V(z)≤-α3(|z|)

(23)

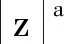
定理1：針對標稱系統式(9)，采用所設計的MPC控制律式(17)，選取滿足優化問題式(16)的正定權值矩陣，Q，R，Qf，則控制律式(17)可使標稱系統式(9)在滿足控制輸入約束式(10)的條件下對于原點指數穩定。

基于引理可推導出定理1，因定理1與定理2的證明過程相似，在此定理1的證明步驟可簡要概述為：

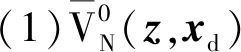
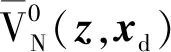
(24)

(25)

如果終端代價函數Vf(·)∈f，那么可得到的遞減性

(26)

2.2 輔助控制器

輔助控制器的目的是使實際系統狀態處于以標稱軌跡為中心的Tube內，從而驅使實際系統的狀態到達上述定義的標稱軌跡上，抵消擾動對實際系統的影響，并最終沿著標稱軌跡收斂于原點。則輔助控制器的優化問題為

(27)

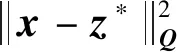
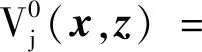
(28)

求解PN(x,z)得到控制序列和對應的最優狀態序列為

u0(x,z)={KN(x,z),u0(1;x,z),…,u0(N-1;x,z)}(29)

x0(x,z)={x,x0(1;x,z),…,x0(N;x,z)}

(30)

式中，第一個元素KN=u0(0;x,z)為應用于模型預測控制的控制律。

假設：在系統x+=f(x,u)中存在控制輸入u∈，終端代價函數Vf∈Xf，則存在

Vf(x+)-Vf(x)≤-l(x,u)

(31)

定理2：針對帶有擾動的實際系統式(7)，采用所設計的輔助控制律式(29)，選取滿足優化問題式(27)的正定權值矩陣，Q，R，Qf,則控制律式(29)可使實際系統式(7)在滿足控制輸入約束式(8)條件下有限時間內趨于穩定。

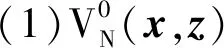
式中：c1>0;λmin{Q}為Q的最小特征值。

當N=1時，由式(28)可得

(33)

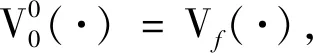
(34)

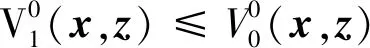
(35)

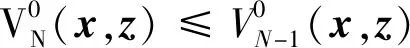
(36)

當N=j+1時，由式(28)可得

(37)

由于Kj不一定為Pj+1(x,z)的最優解，那么可得

(38)

由式(36)可推出

(39)

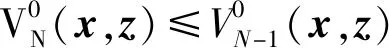
因此,

(40)

式中:c2>c1>0;λmax{P}為P的最大特征值。

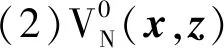
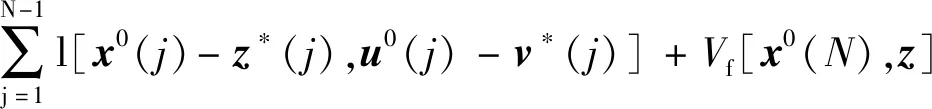
其中,

u0(x,z)=[u0(0;x,z),u0(1;x,z),…,u0(N-1;x,z)](42)

x0(x,z)=[x0(0;x,z),x0(1;x,z),…,x0(N;x,z)](43)

由式(41)可得

(44)

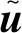
Vf[x+(N),z]

(45)

其中，

u0(x+,z)=[u0(0;x+,z),u0(1;x+,z),…,u0(N-1;x+,z)](46)

x0(x+,z)=[x0(0;x+,z),x0(1;x+,z),…,x0(N;x+,z)] (47)

(48)

則

l[x0(N)-z(N),u-v]+Vf[x+(N),z]

(50)

由式(31)可得

(51)

(3)有限時間穩定性證明

由式(51)可得

(52)

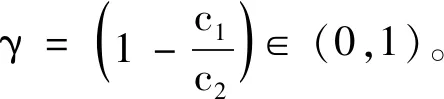
通過不斷迭代式(52)可得

由式(32)、式(40)可得

(54)

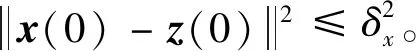
根據上述設計的基于Tube的模型預測姿態控制器，基于Tube的模型預測控制算法可總結如下：

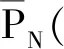
步驟2求解輔助控制器的優化問題PN(式(27))得到當前控制律u=KN。

步驟3將控制律u應用到實際系統(式(6))中得到對應的系統狀態。

3 主動振動控制器設計

為使撓性附件振動進一步得到抑制，將基于壓電智能材料的主動振動控制應用于撓性航天器的振動抑制中，從而提高撓性航天器快速機動時的控制精度。本文采用在撓性航天器表面安裝壓電陶瓷作動器的全階滑模控制方法進行主動振動控制器設計。

根據式(14)設計滑模面為

(55)

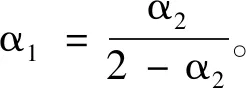
則

up=ueq+h-1un

(56)

(57)

(58)

m=-(kd+kT+n)sgns

(59)

式中：式(58)等價于一個低通濾波器；m為濾波器的輸入;un為濾波器的輸出;T為濾波器的帶寬;ueq為等效控制；un(0)=0;參數kT,kd,n和T均為正定的。

定理3：對于撓性系統式(14)，在全階滑?？刂坡墒?56)的作用下，選取合適的控制參數，那么在有限時間內可以使撓性模態η收斂到零。

證明：將式(14)和式(56)代入式(55)，得到

將式(57)代入式(60)，得到

s=un

(61)

式(58)解為

un(t)=[un(t0)+(1/T)(kd+kT+n)sgns]et-t0-

(1/T)(kd+kT+n)sgns,T≠0

(62)

當t0=0時，un(0)=0，由式(62)可得

(63)

將式(63)等式兩邊同時乘sT，得到

(64)

則

(65)

從而可得

(66)

取李雅普諾夫函數為

(67)

對式(67)求導

(68)

將式(59)代入式(68)，得到

(69)

因此

(70)

通過式(66)可得到

(71)

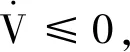
基于以上分析，本文的主要控制思想是首先求解標稱模型預測控制問題(式(16))生成標稱軌跡，再將通過輔助控制器得到的控制律(式(29))應用于實際系統得到實際狀態，使實際狀態保持在以標稱軌跡為中心的Tube不變集內，從而驅使實際軌跡態到達標稱軌跡上，并最終收斂至原點，使姿態角快速穩定地達到期望姿態且有效減少擾動對姿態角的影響，同時利用全階滑模主動振動控制器(式(56))抑制撓性附件帶來的振動，使撓性振動模態衰減趨于零。

4 仿真研究

將本文提出的Tube-MPC姿態控制器和全階滑模主動振動控制器應用于撓性航天器中，為驗證控制器的有效性，進行仿真驗證與分析。選取文獻[24]的撓性航天器模型參數：

轉動慣量J為

撓性航天器的中心剛體和撓性附件間的耦合矩陣為

壓電作動器與撓性附件間的耦合矩陣為

本章考慮具有四階撓性模態的情況，自然頻率為Ω1=0.768 1 rad/s，Ω2=1.103 8 rad/s，Ω3=1.873 3 rad/s，Ω4=2.549 6 rad/s，阻尼為ξ1=0.005 6，ξ2=0.008 6，ξ3=0.013 0，ξ4=0.025 0。

在仿真中，初始角速度的值為ω(0)=[0 0 0]Trad/s；期望值為ωd=[0 0 0]T;初始MRPs值為σ(0)=[-0.224 25 0.672 78 -0.448 52]T；期望值為σd=[0 0 0]T。

干擾力矩為

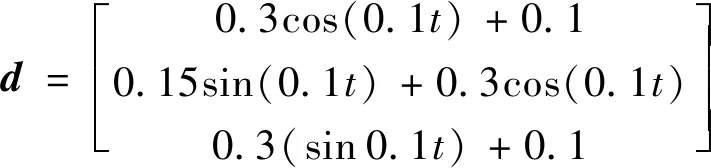
控制力矩受限為-30(Nm)≤u≤30(Nm)，預測時域N=5。

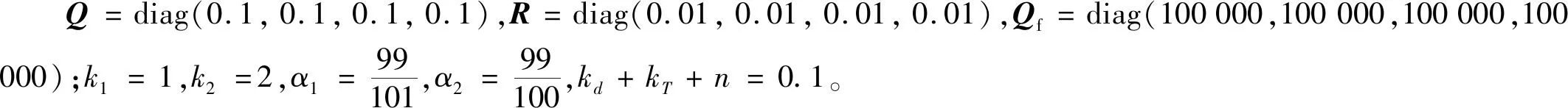
針對撓性航天器分為不采用主動振動控制器和采用主動振動控制器兩種情況進行仿真研究。

當不采用主動振動控制器時，為了加以比較，姿態控制器分別采用本文所設計的基于Tube的模型預測控制器和經典的非線性模型預測控制器，對兩類控制系統做仿真研究，仿真結果如圖1～圖4所示。在NMPC控制下的姿態角和角速度響應時間在40 s左右，撓性附件振動較大，從而使跟蹤精度較低，穩態誤差較大；而在基于Tube的模型預測控制器下的姿態角和角速度響應時間在30 s左右，撓性附件振動較小，從而使跟蹤精度較高，穩態誤差較小，系統的實際狀態可快速跟蹤上標稱軌跡的姿態，并最終收斂至原點，可有效降低擾動對系統的影響。同時從圖4中可以看到，僅依靠基于Tube的模型預測姿態控制器，航天器的撓性模態也得到了較好的控制，但撓性振動依然無法快速衰減。因此，有必要將主動振動控制器應用到振動抑制中。

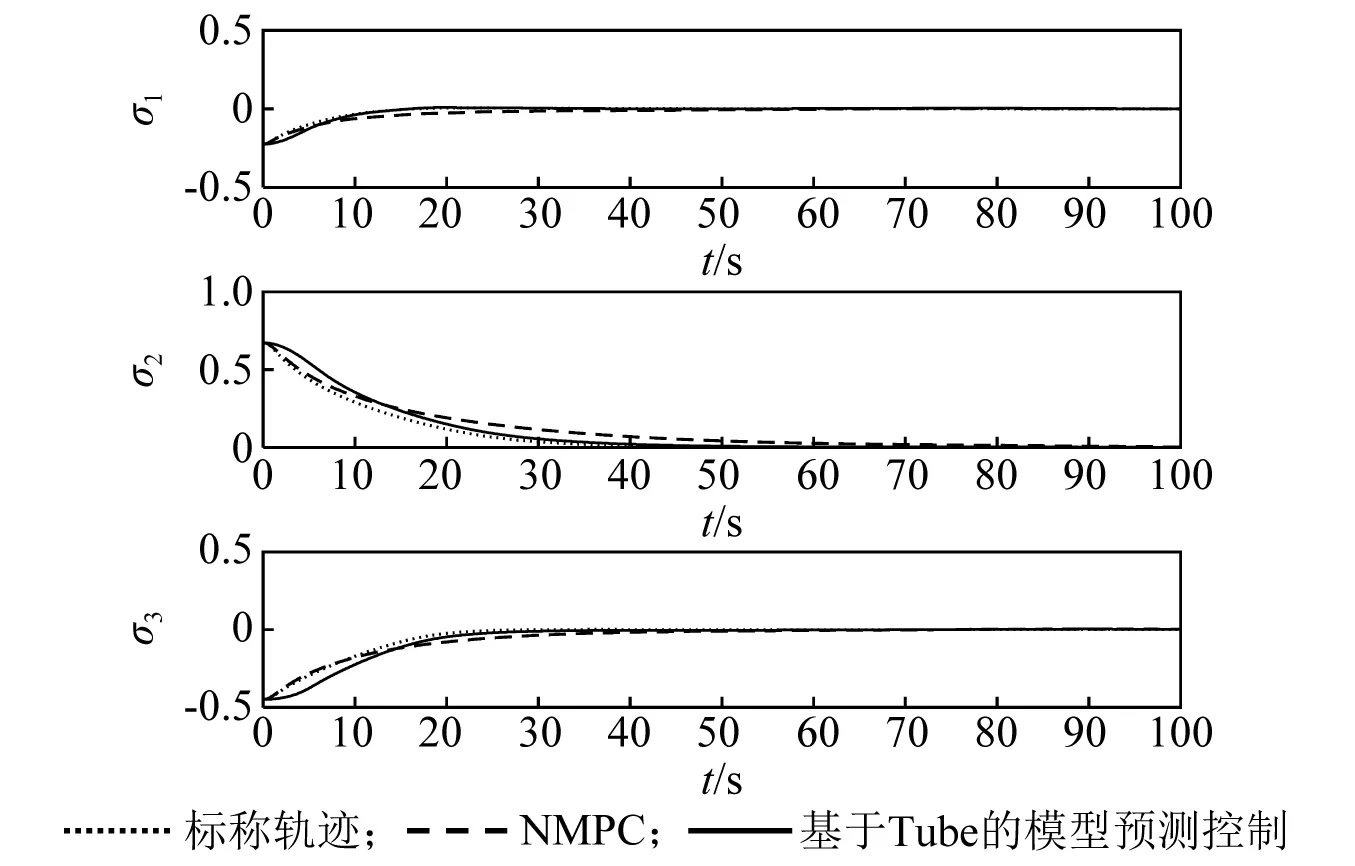
圖1 姿態角變化曲線Fig.1 The response of MRPs

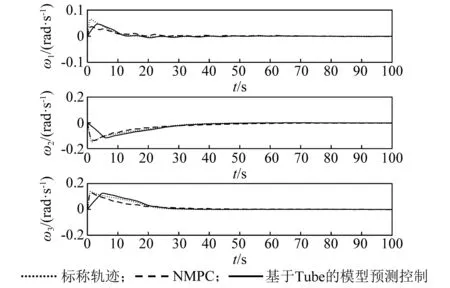
圖2 角速度變化曲線Fig.2 The response of angular velocity

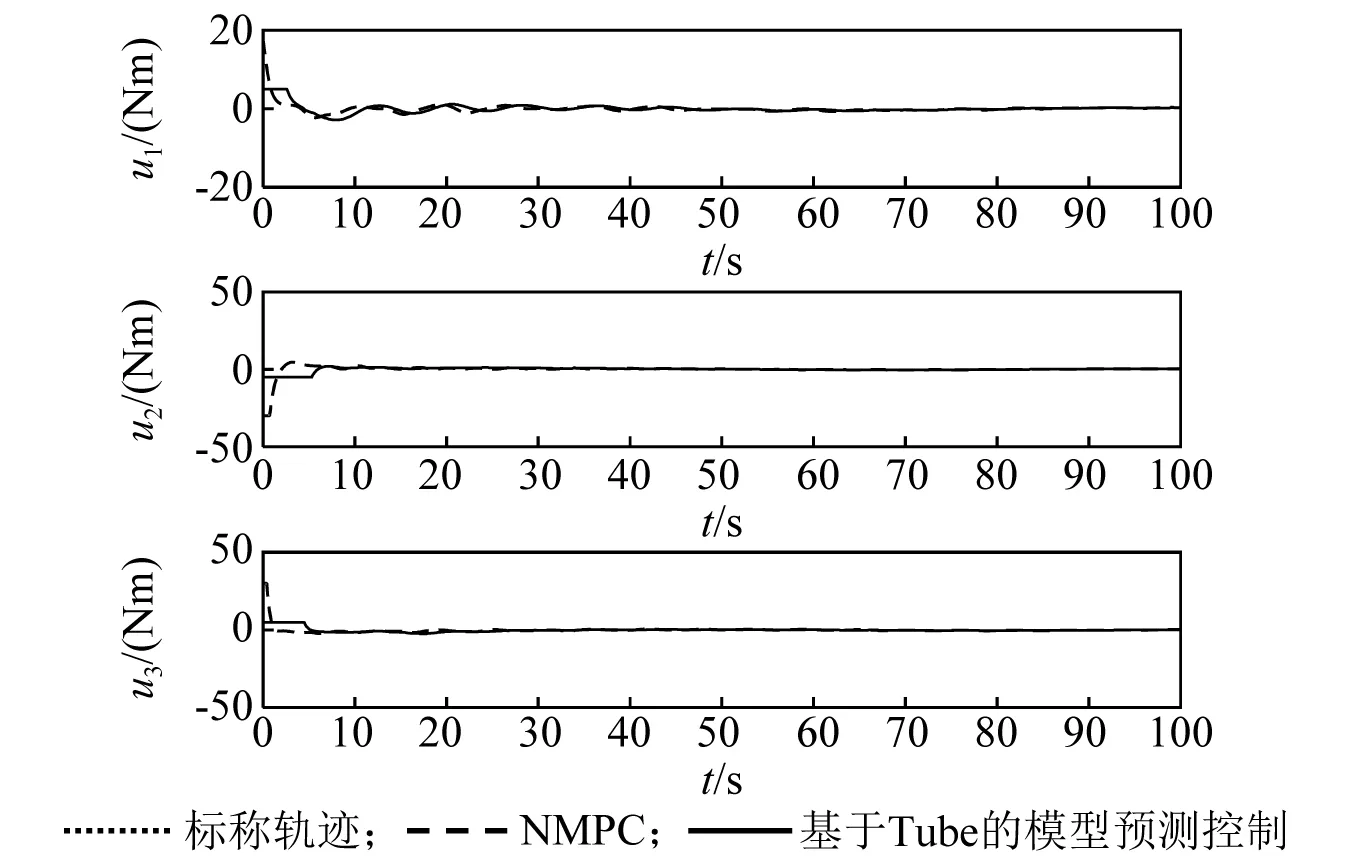
圖3 控制輸入變化曲線Fig.3 The response of control torque

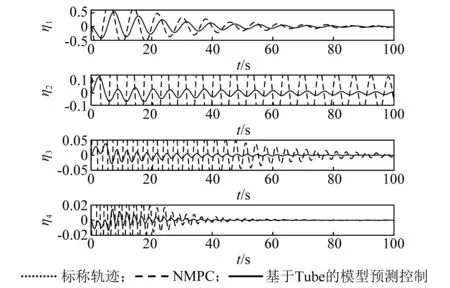
圖4 撓性模態變化曲線Fig.4 The response of vibration displacements

當采用主動振動控制器時，為驗證所設計的全階滑模振動控制器的有效性，主動振動控制器分別采用本文所設計的全階滑?？刂破骱统Ｓ玫哪B速率反饋(modal velocity feedback，MVF)控制器(文獻[25])，而姿態控制器均采用NMPC控制器。對這兩類控制系統做仿真研究，仿真結果如圖5～圖9所示。在MVF控制下的撓性附件振動較大，撓性模態在25 s左右衰減至零，導致對應的姿態角和角速度收斂較慢；在全階滑?？刂葡碌膿闲愿郊駝虞^小，撓性模態均在15 s內快速衰減至零，從而使對應的姿態角和角速度收斂速度較快，可有效抑制撓性模態抖振，具有良好的振動抑制效果。故在姿態控制器均采用NMPC控制器時，主動振動控制采用全階滑?？刂破骺墒箵闲阅B快速收斂至零，從而使姿態角和角速度比采用MVF主動振動控制時的收斂速度更快，跟蹤精度更高。

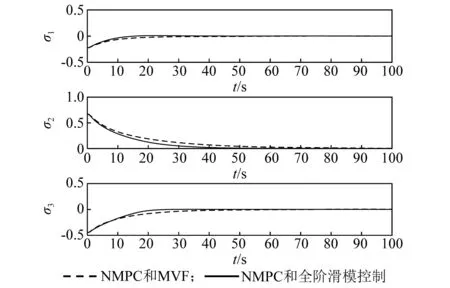
圖5 姿態角變化曲線Fig.5 The response of MRPs

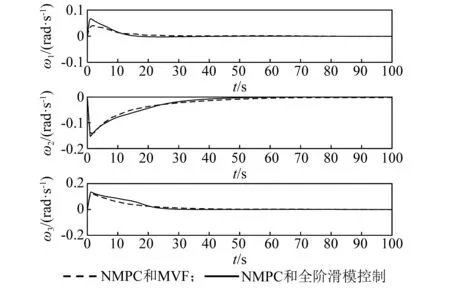
圖6 角速度變化曲線Fig.6 The response of angular velocity

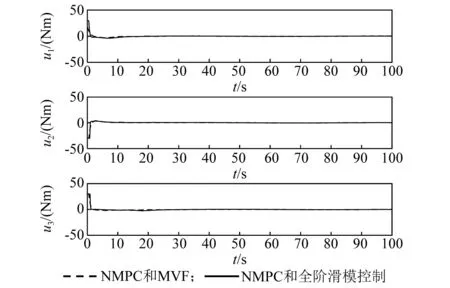
圖7 控制力矩變化曲線Fig.7 The response of control torque

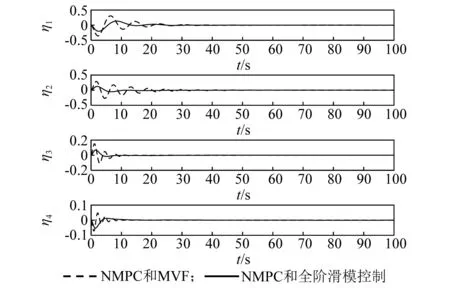
圖8 撓性模態變化曲線Fig.8 The response of vibration displacements

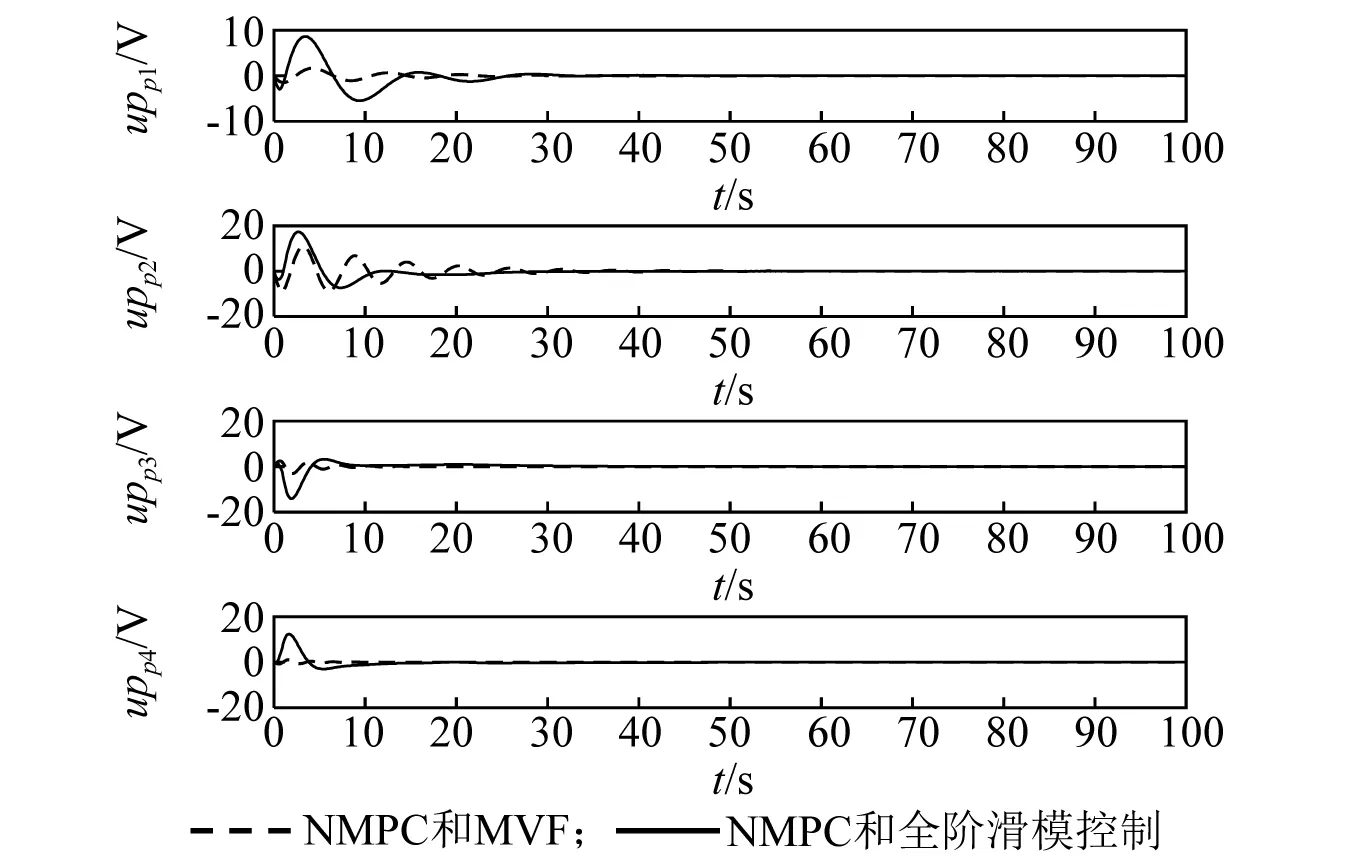
圖9 控制電壓變化曲線Fig.9 The response of input voltage

為進一步驗證所設計的Tube-MPC姿態控制器與全階滑模振動控制器相結合對撓性航天器姿態機動控制的有效性，姿態控制器分別采用基于Tube的模型預測控制器和NMPC控制器，主動振動控制器均采用全階滑?？刂破?，對這兩類控制系統做仿真研究，仿真結果如圖10～圖14所示。在NMPC和全階滑模振動控制下，初始階段的前四階撓性振動模態最大值分別為0.20，0.17，0.08，0.05，撓性模態在15 s左右衰減至零，對應的姿態角和角速度收斂時間約為30 s；在基于Tube的模型預測控制和全階滑模振動控制下，初始階段的前四階撓性振動模態最大值分別為0.080，0.050，0.015，0.010，撓性模態在5 s內快速衰減至零，對應的姿態角和角速度收斂時間約為20 s。故從仿真結果圖10～圖14可看出，所設計的基于Tube的模型預測姿態控制和全階滑模振動控制，可有效抑制撓性模態抖振，具有更好的振動抑制效果，從而使姿態角和角速度收斂速度更快，跟蹤精度更高。

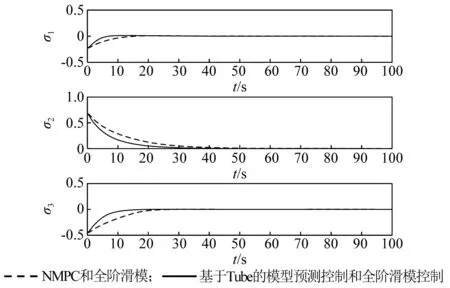
圖10 姿態角變化曲線Fig.10 The response of MRPs

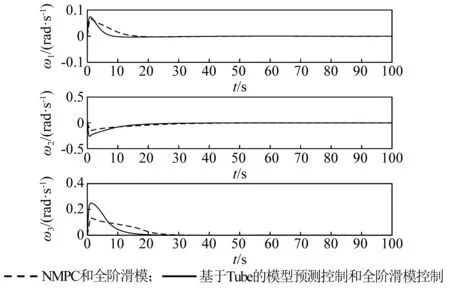
圖11 角速度變化曲線Fig.11 The response of angular velocity

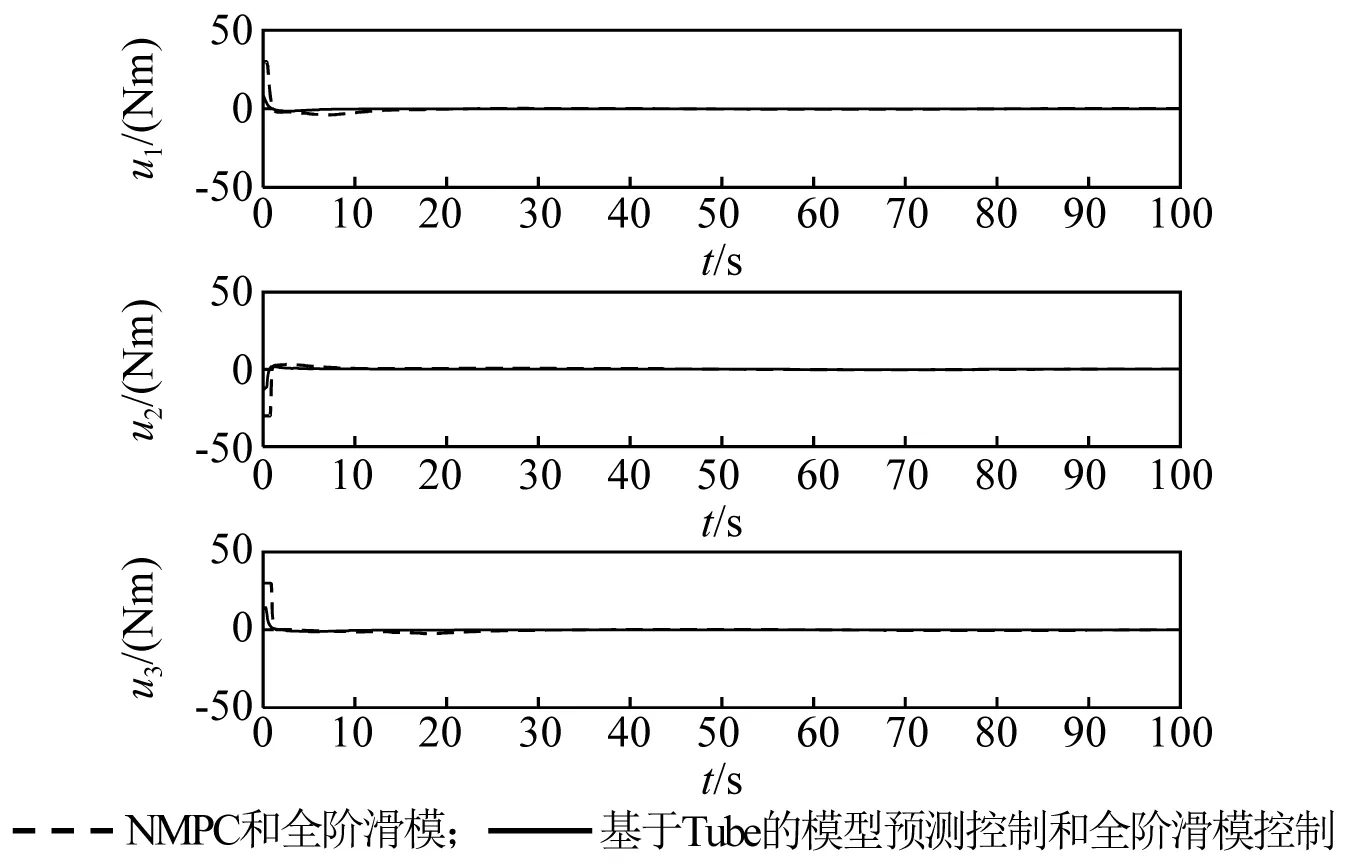
圖12 控制力矩變化曲線Fig.12 The response of control torque

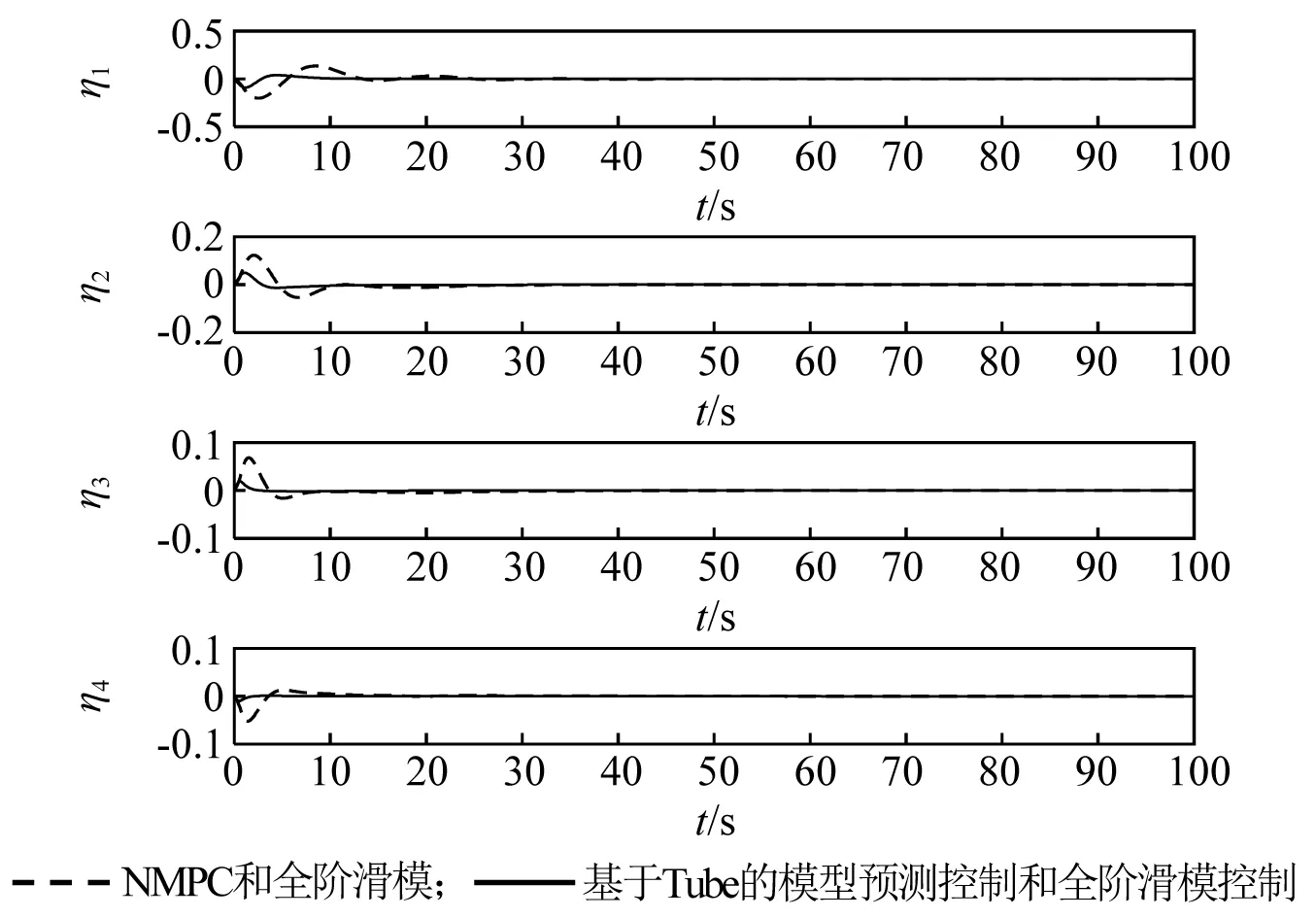
圖13 撓性模態變化曲線Fig.13 The response of vibration displacements

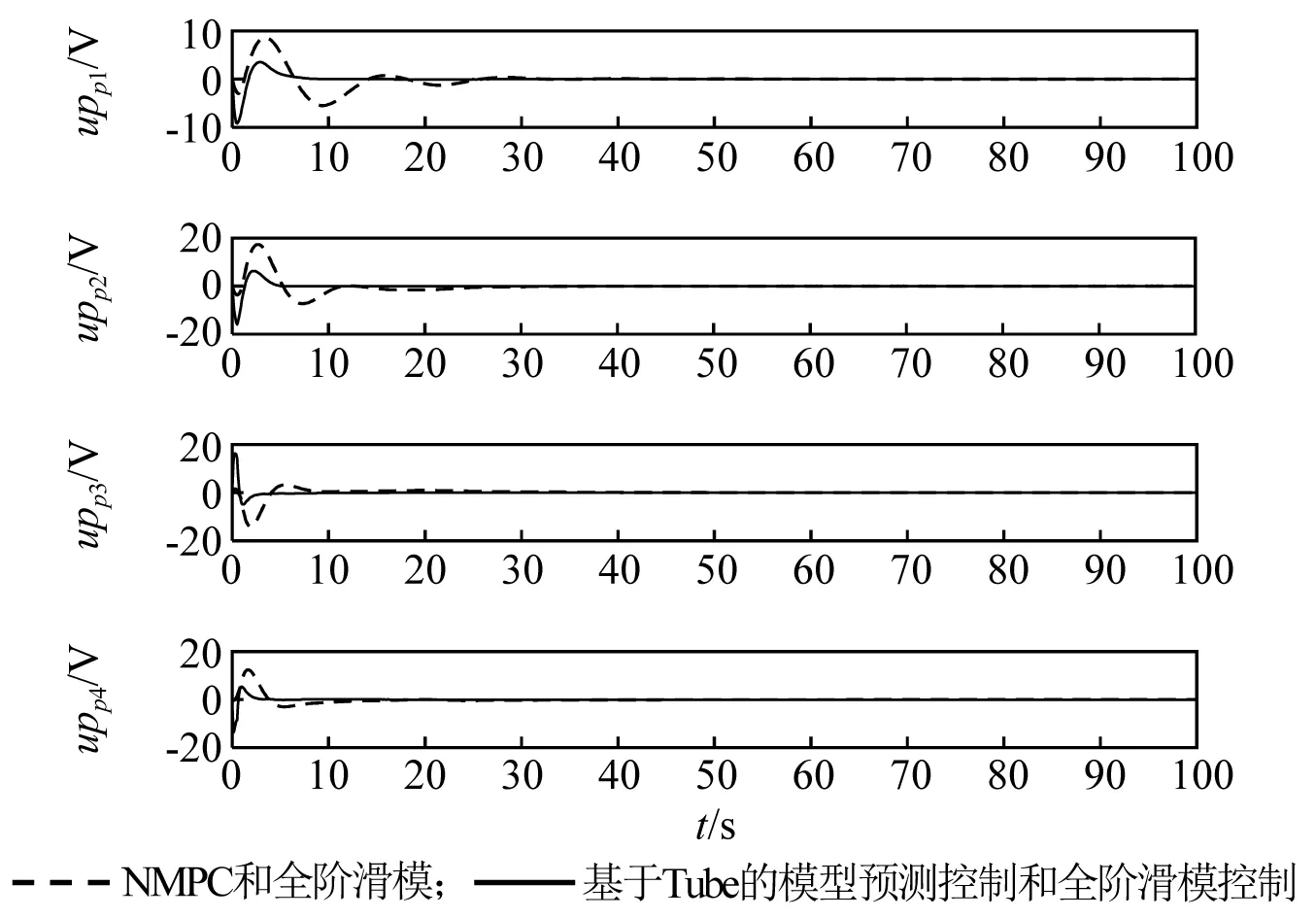
圖14 控制電壓變化曲線Fig.14 The response of input voltage

由上述仿真結果可看出，在具有撓性附件振動和外部擾動作用時，基于Tube的模型預測控制可使實際系統狀態保持在以標稱軌跡為中心的Tube內，抗干擾能力較強，且實際系統狀態可快速到達標稱軌跡上，并最終收斂至原點，故基于Tube的模型預測姿態控制系統的響應快，穩態誤差小，得到比NMPC作用下更好的控制效果。而本文所設計的全階滑模主動振動控制器，在有效抑制傳統滑模抖振的同時使撓性振動模態在有限時間內快速衰減為零。因此本文所提出的控制方法在具有基于Tube的模型預測姿態控制器的優勢下，結合全階滑模主動振動控制器，能更有效地抑制撓性附件振動，從而使姿態控制系統響應時間更短，跟蹤精度更高，且撓性振動衰減更快，具有較好的動、穩態特性。

5 結 論

本文針對撓性航天器大角度姿態控制問題，將Tube-MPC控制理論、全階滑模控制理論、主動振動控制技術結合應用于撓性航天器系統。在有撓性附件振動和外部擾動作用時，基于 Tube的模型預測姿態控制器可使實際系統狀態保持在以標稱軌跡為中心的Tube不變集中，并驅使實際系統狀態到達標稱軌跡上，從而沿著標稱軌跡最終收斂至原點，抗干擾能力較強，使姿態角實現快速跟蹤。同時設計了全階滑模主動振動控制器，全階滑模有效減少了撓性附件的振動。仿真結果表明，所提出的Tube-MPC姿態控制系統，可確保振動模態快速收斂到零，既能快速而穩定的跟蹤期望指令，又能保證良好的控制精度。