基于跟馳模型的智能網聯汽車混合交通流分析

趙輝

（蘭州石化職業技術大學，甘肅 蘭州 730060）

0 引 言

近年來，隨著車輛擁堵、事故頻發等交通問題的凸現，無人駕駛技術的研究變得尤為重要。美國汽車工程師學會將車輛自動駕駛等級劃分為無自動駕駛（L0）、輔助駕駛（L1）、部分自動駕駛（L2）、有條件自動駕駛（L3）、高度自動駕駛（L4）及完全自動駕駛（L5）六類。隨著無人駕駛技術的不斷發展，智能網聯車將逐漸普及。研究表明，預計2045年道路上L4 級別的智能網聯汽車滲透率僅能達到24.8%。因此，未來很長一段時間內，人類駕駛車輛還會存在，道路上將普遍呈現由常規車（regularvehicle, RV）、CAV（connected and autonomous vehicles）組成的混合交通流。這兩種類型的汽車將如何一起運行？本文討論的混合交通流是解決這個問題的常用工具。為了更真實地描述交通動態，人們提出了跟馳模型，跟馳模型作為微觀交通流模型已開發了幾十年，并被廣泛用于描述系統中單個汽車的移動行為，已成為智能交通領域的研究熱點。W.X 等人利用跟馳模型研究了由RV 和CAV 組成的混合交通流的演變。Nakayama 等人提出了一種新的最優速度跟馳模型來研究智能網聯車輛和人類駕駛車輛在跟馳過程中混合交通流的演變。M.BANDO等人創建了智能網聯車輛跟馳過程中的優化速度函數。Ge 等人研究了智能網聯汽車前車加速度反饋控制項模型的穩定性。Coifman基于檢測器數據和交通流理論，估計路段行程時間重構了車輛的運行軌跡。Talebpour 等人利用跟馳模型，分析了智能網聯車輛和人類駕駛車輛對交通流穩定性的影響。Ward通過Lyapunov 穩定性原理對混合交通流穩定性解析方法進行了推導，驗證了智能網聯車輛可實時獲取前車的加速度數據，從而保證車輛的安全與穩定。

鑒于以上研究，本文基于跟馳模型，分析混合交通流穩定性的基本圖。安排如下，在第1 節中，展示了人類駕駛汽車和智能網聯汽車的動力學模型，先后給出了引理和定理。在第2 節中，分別在三種情況下進行了數值的仿真和模擬。在第3 節中，進行了總結。

1 動力學模型

1.1 模型假設

假設1：人類駕駛車輛和智能網聯駕駛車輛的混合交通流在單車道上周期性邊界條件下無超車行為。

假設2：兩種類型車輛共計輛，且均勻分布在道路上。

假設3：道路中只有機動車輛，無其他不可抗力因素。

1.2 人類駕駛車輛模型

Bando的模型用于描述人類駕駛車輛，目前已被多人引用。它被制定為式（1）：

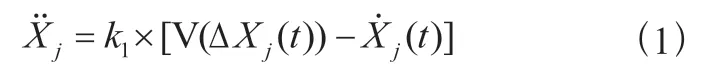
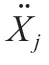
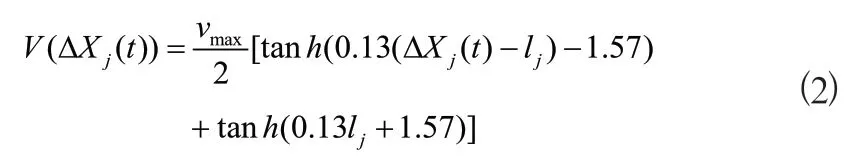
其中表示最大速度，l表示第輛車的長度。

利用線性穩定性理論分析車輛以常數運動的穩態均勻流動周期性邊界條件下的車頭和速度。方程中均勻穩態的解為式（3）：

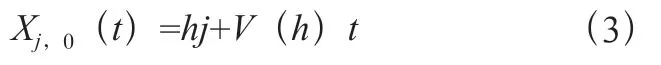
其中，=/，為相同的車頭時距，為道路總長度，為車輛總數系統。根據經典線性系統穩定性理論，引理為：

引理1：如果滿足式（4）中的下述條件：

則在最優速度模型的交通流中不會發生交通擁堵，否則會產生擁堵。

1.3 智能網聯車輛模型

智能網聯汽車安裝有多個傳感器，可以檢測前后車頭時距。基于Bando 的模型，智能網聯汽車模型可以被描述為如式（5）：

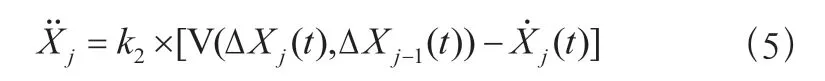
其中是智能網聯汽車上傳感器的靈敏度。（ΔX（），ΔX（））是基于汽車上的前后傳感器，可以描述為式（6）：

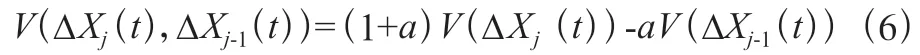
其中是一個常數。由于網聯車內的電子傳感器比駕駛員更敏感，因此靈敏度始終小于。

此模型的理念是，如果前車距大于后車距，那么汽車會具有更大的預期速度；如果前車距小于后車距，那么汽車將獲得較小的預期速度；如果前車距等于后車距，那么汽車將獲得預期的速度。

從上面的思路可以知道，由于因子不僅加強了車流的穩定性，而且也增強了安全性。它使智能網聯汽車盡可能均勻地在道路上行駛。因此，參數模型中的被命名為“平滑因子”。

根據引理1：從上述新模型可以提出如式（7）的定理

定理1：如果滿足以下條

則交通擁堵不會發生在智能網聯駕駛汽車流中。否則，就會產生交通擁堵。

由引理1、定理1 及平滑因素，繪制出中性穩定線，如圖1所示。圖中，中性線以上的區域是非堵塞區域，中性線以下是堵塞區域。在=0 時，臨界點是（17.59，1.913）。由上圖可以得知，平滑因子越大意味著穩定區域越大。

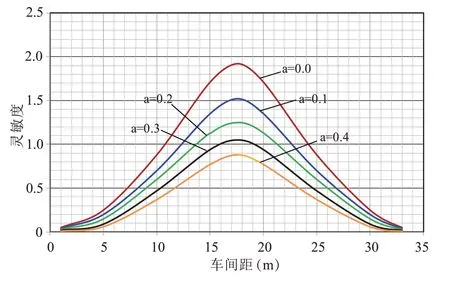
圖1 不同平滑因子的中性穩定線

2 數值模擬

在周期性邊界條件下，道路上的輛車沒有超車的路程長度是米。汽車序列號是從第0 到第（-1）輛，第輛是該系統中的第一輛汽車。讓[][] 和[][] 表示第輛車在時間的速度和位置。設定最佳速度函數為14.67 m/s，兩種類型車輛的長度均相同，進行仿真。

2.1 靈敏度和平滑因子均不同的交通流模擬

本節將在兩種情況下分別進行模擬，一為100%智能網聯汽車交通流，二為50%智能網聯汽車與50%人工駕駛汽車混合交通流。期間，交通流的變化密度可以通過兩種方式實現。

首先，道路長度不變，汽車數量按固定值依次增加。表達式如式（8）：

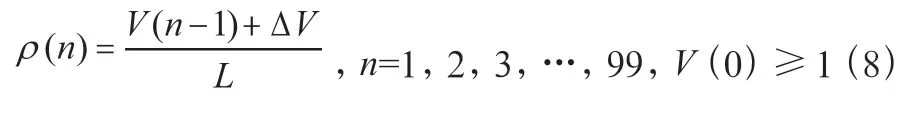
其中（）表示第次模擬的車輛數量，Δ是車輛的固定增加量。

其次，車號不變，道路長度按固定值依次遞減。表達式如式（9）：

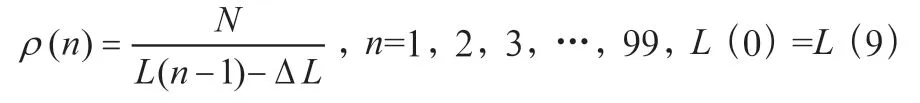
其中（）表示第次模擬的道路長度，Δ是固定減少的道路長度。交通流量的通量采用式（10）表示：

其中表示通量，表示流動密度，是一段時間內流動的平均速度。

2.1.1 100%智能網聯汽車模擬

設定道路長度為=1 800 m，依次在系統中加入固定數量的智能網聯汽車。根據式（10），每次增加5 輛智能網聯汽車，共100 次。在以下兩種情況下進行了模擬：不同的靈敏度=1.0、1.26、1.66、2.04 和平滑因子=0.0；仿真結果如圖2所示。從圖中可以觀察到，基本圖中存在臨界點（ρ，Q）。當密度小于臨界密度ρ時交通流的通量越大，對應的靈敏度也越大；當密度為大于臨界密度ρ時，交通流的通量越大，對應的靈敏度越小。同理，模擬仿真變化的平滑因子=0.1、0.2、0.3、0.4 和靈敏度=1.0，可以得到類似的結論：平滑因子對交通流量有相同的影響，即在臨界密度ρ之前，平滑系數越大，交通流量越大；在臨界密度ρ之后，交通流量的變化呈相反趨勢。

圖2 不同靈敏度下智能網聯汽車流動基本圖

2.1.2 50%智能網聯汽車與50%人工駕駛汽車模擬

此數值模擬以檢測混合交通流中靈敏度和平滑因子的影響。當平滑因子不變=0.0，靈敏度取值分別為=1.0、1.26、1.66、2.04 時，仿真結果如圖3所示。可以看出，靈敏度越大，在臨界密度之前獲得較大的交通流量，在臨界點之后呈現相反的變化趨勢。同理，當靈敏度不變=1.0，平滑因子取值分別為=0.1、0.2、0.3、0.4 時，可以得到類似的結論，即平滑因子越大，在臨界密度之前獲得較大的交通流量，在臨界點之后呈現相反的變化趨勢。

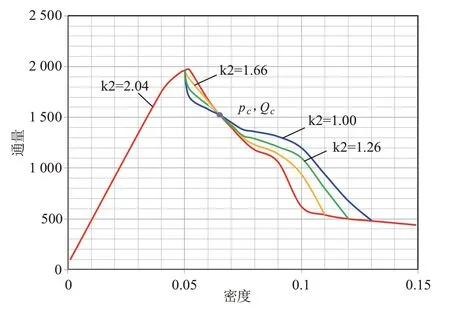
圖3 不同靈敏度下的混合交通流的基本圖

從以上模擬可以得出結論，無論是智能網聯車流還是人類駕駛車輛與CAV 的混合交通流，通量在一定的密度范圍內受靈敏度和平滑因素的影響。且對比圖2和圖3，可以看出，圖3的密度變化范圍明顯大于圖2，即混合交通流的穩定性弱于智能網聯汽車流的穩定性。

2.2 智能網聯車流穩定性模擬

2.2.1 不同靈敏度下交通流的穩定性

此模擬中，道路長度為1 800 m，智能網聯汽車的數量為100 輛，靈敏度取以下值：=0.83、1.26、1.66、2.04，不考慮平滑因素。仿真結果如圖4所示，圖（a）和圖（b）分別對應于=0.83，=0 和=0.24，=0，圖中的模式展示了在時間=19 000 s 時智能網聯汽車的前進曲線，可以看出，隨著靈敏度的逐漸增大，智能網聯駕駛車流的穩定性隨之加強。因此可以得出：智能網聯汽車流的穩定性可以通過以下方式增強：更大的靈敏度。

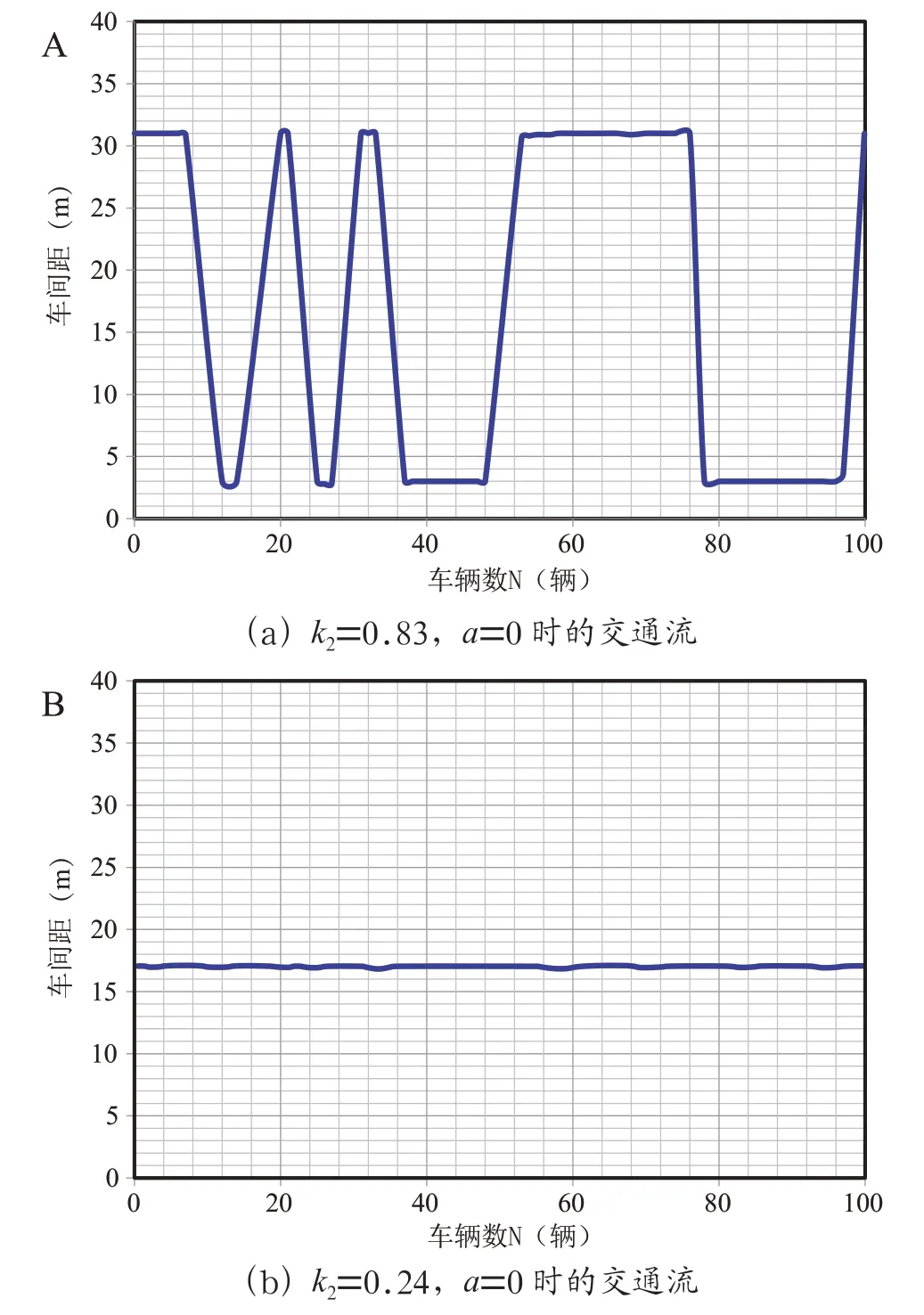
圖4 不同靈敏度下智能網聯車交通流的時距圖

2.2.2 不同平滑因子下交通流的穩定性

此模擬中，靈敏度取為=1.0，平滑因子取為=0.1、0.2、0.3、0.4。采用與2.2.1 相同方法，仿真出具有不同平滑因子的智能網聯汽車在=19 000 s 時的車頭時距曲線。可以得出相似的結論：智能網聯駕駛車流的穩定性隨著平滑因子的增加而增強。即智能網聯車流的穩定性還可以通過另一種方式得到增強：更大的平滑因子。

2.3 混合交通流穩定性模擬

2.3.1 不同靈敏度下混合交通流的穩定性

此模擬中，混合交通車流總數為100，道路長度為1 800 m。智能網聯汽車中靈敏度取值依次增大，分別為：=0.83、1.26、1.66、2.04，平滑因子取0，不考慮CAV的后車距。如圖5展示了在=19 000 s 時不同靈敏度的混合交通流，圖5（a）和圖5（b）分別對應于（=0.83，=0.83，=0）和（=0.83，=2.04，=0）。從圖中可以觀察到，車頭時距振蕩的幅度隨著靈敏度的提高而變小。這意味著混合車流的穩定性隨著靈敏度的增加而加強。

圖5 不同靈敏度下混合交通流的時距圖

2.3.2 不同平滑因子下混合交通流的穩定性

此模擬檢驗了不同平滑因子=0.1、0.2、0.3、0.4 對混合交通流穩定性的影響。采用與2.3.1 相同方法，仿真出具有不同平滑因子的智能網聯汽車=19 000 s 時的車頭時距曲線。智能網聯駕駛汽車的靈敏度取值為=2.5。可以得出相似的結論：車頭時距振蕩的幅度隨著平滑因子的增大而變小，即隨著平滑因子的增加，混合交通流的穩定性得到了加強。

3 結 論

本文分析研究了人類駕駛汽車和智能網聯駕駛汽車混合的交通流。首先提出了一種具有靈敏度和平滑因子可調的智能網聯駕駛汽車數學模型，并且基于定理進行了穩定性分析。得出在一定范圍內，靈敏度和平滑因子可以影響車流的穩定性。

建立了三種不同車流的結構模型，通過模擬仿真，得出結論：（1）在一定邊界條件下，100%智能網聯汽車交通流的穩定性強于混合交通流的穩定性。（2）通量在一定的密度范圍內受靈敏度和平滑因素的影響，隨著靈敏度和平滑因子的增大，智能網聯駕駛車流及混合交通流的穩定性均隨之加強。即智能網聯車流和混合交通流的穩定性可以通過以下兩種方式增強：更大的靈敏度和更大的平滑因子。