FAHP-CRITIC欺騙干擾設備效能評估仿真分析

尹繼澤，鄧杏松

(中國船舶集團有限公司第八研究院，江蘇 揚州 225101)

0 引 言

為了提高反艦導彈威脅下艦船的生存概率，欺騙干擾設備通過模擬艦船的雷達回波形成假目標，誘導采用主動式尋的制導的反艦導彈捕獲、跟蹤、命中假目標。為了持續優化欺騙干擾設備的干擾決策和干擾參數，需要對干擾效果進行監視。干擾效果最終表現為被干擾的雷達系統功能和性能的變化，通常只能根據偵察接收機接收到的雷達發射信號變化進行分析和判斷，但其中體現的雷達系統功能和性能的變化有時并不明顯，導致分析判斷不全面、不充分，因此，有必要研究效能評估方法。

目前已經存在多種效能評估方法，包括基于相關指標進行分析，模數轉換(ADC)模型法，層次分析法(AHP)，灰色關聯法，模糊層次分析法(FAHP)，以及機器學習等。由于欺騙干擾發生在復雜電磁環境中，其效能與設備的信號處理能力、干擾參數、軟硬件性能等有關，這些因素對于效能的影響存在模糊性，只有模糊層次分析法可以處理模糊信息。現有的基于模糊層次分析法的效能評估方法具有以下問題：

(1) 依賴專家知識，具有一定的主觀性，無法根據試驗數據快速做出客觀判斷，實時性較差；

(2) 隨著效能指標的增多，不同指標之間具有一定的關聯性，憑經驗難以分析；

(3) 隨著干擾方案、干擾對象等因素的變化，同一指標在多組數據中展現的波動性未得到利用。

為處理以上問題，引入沖突相關性賦權法(CRITIC)。它是由Diakoulaki提出的一種客觀權重賦權法，結合不同指標之間的關聯性和同一指標在多組數據中展現的波動性，確定各指標對應的權重，避免專家打分帶來的主觀性因素影響和滯后性。CRITIC方法目前已在空戰等領域得到應用。

提出一種FAHP-CRITIC欺騙干擾設備效能評估方法，能夠有效緩解王月等人指出的模糊性與關聯性兼顧問題和賦權的主觀性問題，同時引入波動性。本文通過數值仿真驗證該方法的有效性。

1 基礎知識

效能評估的基本步驟是：(1)選取并通過試驗得到反映干擾能力的效能指標；(2)確定各指標的權重；(3)運用評估方法得出評估結果。對欺騙干擾設備進行效能評估，依賴多個相關的效能指標，因為不同效能指標對效能評估結果的影響程度不同，故使用層次分析的方法對效能指標進行平衡。因為效能指標與效能評估結果之間的關系存在模糊性，即兩者無法準確映射，故使用模糊綜合評判(FCA)的方法。

1.1 層次分析法

層次分析法先將目標分解為多個目標或準則，再迭代分解為更多的準則或指標，構成若干個層級，從而根據各級單排序權重進行多指標的優化決策。在本文中，將效能評估的目標分解為計算多個效能指標，基于CRITIC法計算權重，通過模糊綜合評判來得出最終的分數。

1.2 模糊綜合評判法

模糊綜合評判法根據模糊數學的隸屬度理論，把定性評價轉化為定量評價，對受到多因素制約的對象做出一個系統性的、清晰的評價。在本文中，通過隸屬函數確定等極化處理后的效能指標對應的不同評價區間的隸屬度，與評價集合一同加權運算后得到評價分數作為效能評估結果。

2 FAHP-CRITIC欺騙干擾設備效能評估方法

2.1 指標定權

基于多種準則，把反映欺騙干擾設備效能的指標進行綜合處理，以層次結構模型為基礎建立指標體系。參考王月等人的工作，如表1所示，指標體系劃分為目標層、準則層和指標層：準則層是效能評估的一級指標集；指標層是效能評估的二級指標集，將定性評估轉化為定量評估。

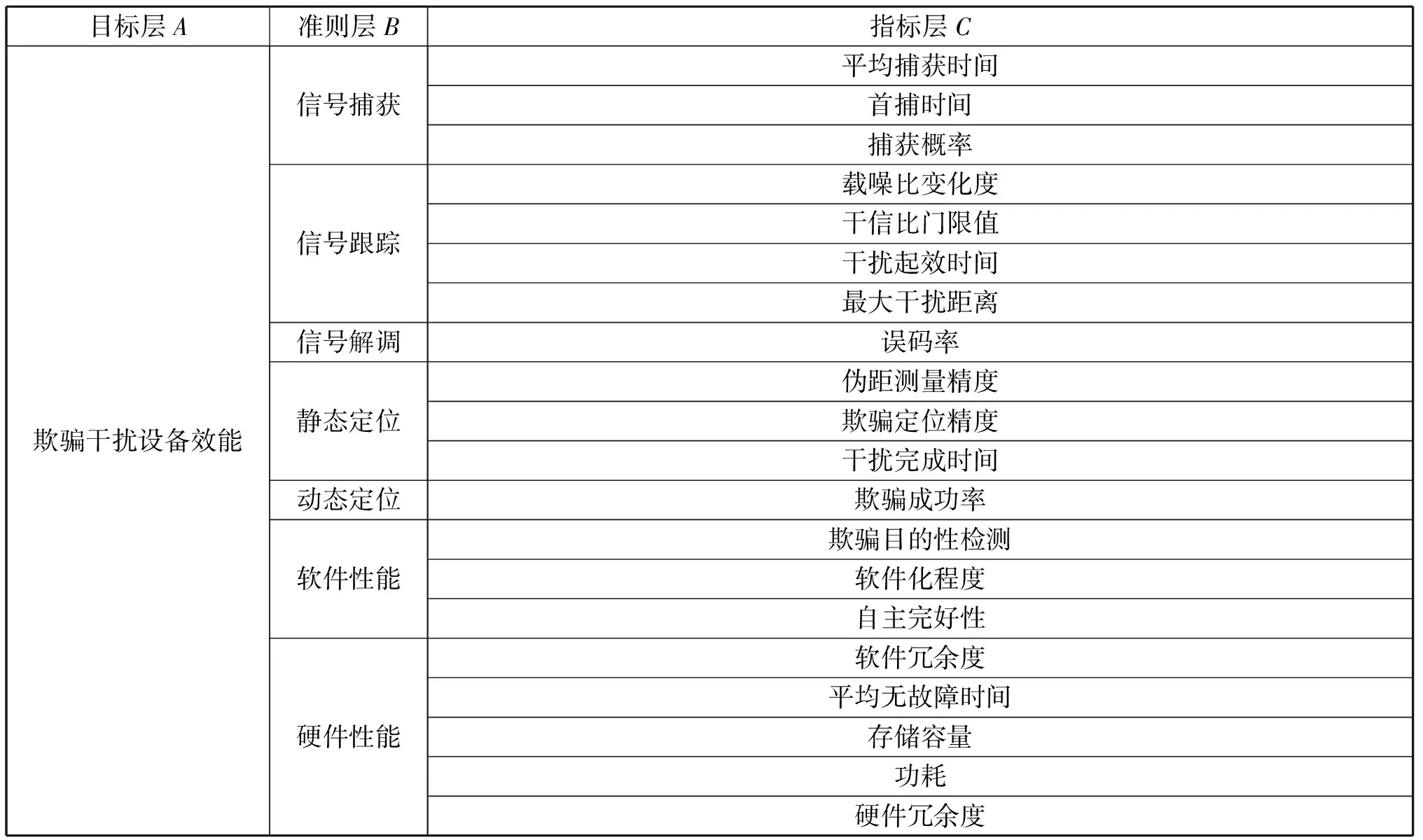
表1 指標體系

各效能指標具有不同的單位和數量級，需要先進行等極化處理使其處于區間[0,1]內。指標分為正向型(評估值越大，指標性能越優)和負向型(評估值越小，指標性能越優)，當存在若干組多類別的效能指標(是指標編號，是組號)時，正向型指標經過等極化處理后為：

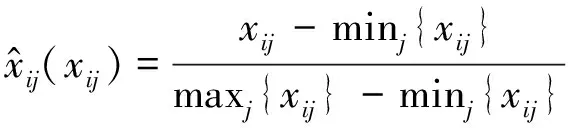
(1)

負向型指標經過等極化處理后為：

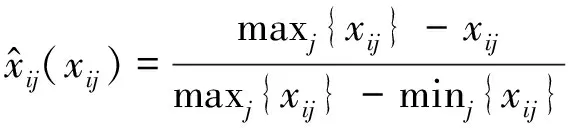
(2)

接下來進行指標定權，確定各指標在效能評估中的重要性，具體方法包括主觀和客觀賦權法。其中，主觀賦權法是根據專家經驗，對某層指標相對上一層級的重要性兩兩比較得到判斷矩陣，再計算指標權重。客觀賦權法則根據原始數據之間的關系通過一定的數學方法來計算指標權重，不依賴人的主觀判斷。

CRITIC法是一種客觀賦權法，結合指標的關聯性和波動性，確定各指標對應的權重。不同指標之間的關聯性用相關系數表示，如果2個指標之間具有較強的正相關性，說明二者相近，權重會降低。同一指標在多組數據中展現的波動性用標準差表示，如果標準差大，說明該指標隨某些因素變化而增減的幅度較大，權重會提高。

因此，第個指標包含的信息量表示為：

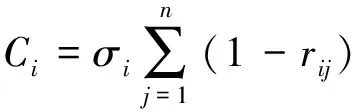
(3)

式中：為指標的數目。

越大，說明第個指標的相對重要性越大，故其客觀權重為：

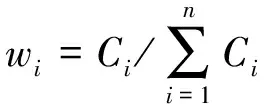
(4)

2.2 效能評估

在指標定權后，可以得到一級單排序權重向量和二級單排序權重向量：

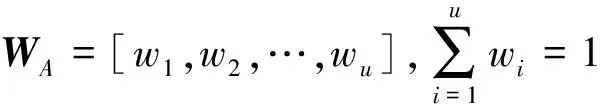
(5)

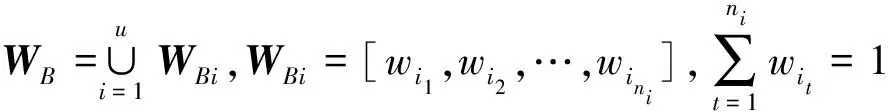
(6)

式中：為第個準則對應的指標數目。

根據效能評估的實際需求，構建評價集合，包含4個等級：不合格、合格、良好、優秀。為了使評估結果的優劣程度直觀且具有區分度，將定性等級轉化為對應的百分值，即：0～60為不合格，60～70為合格，70～80為良好，80～100為優秀。取評價區間的中間值(不合格的中間值取55)作為量化后的評價集合：

=[55,65,75,95]

根據評價集合的評價區間，使用三角形和半梯形結合的隸屬函數計算隸屬度，如圖1所示。

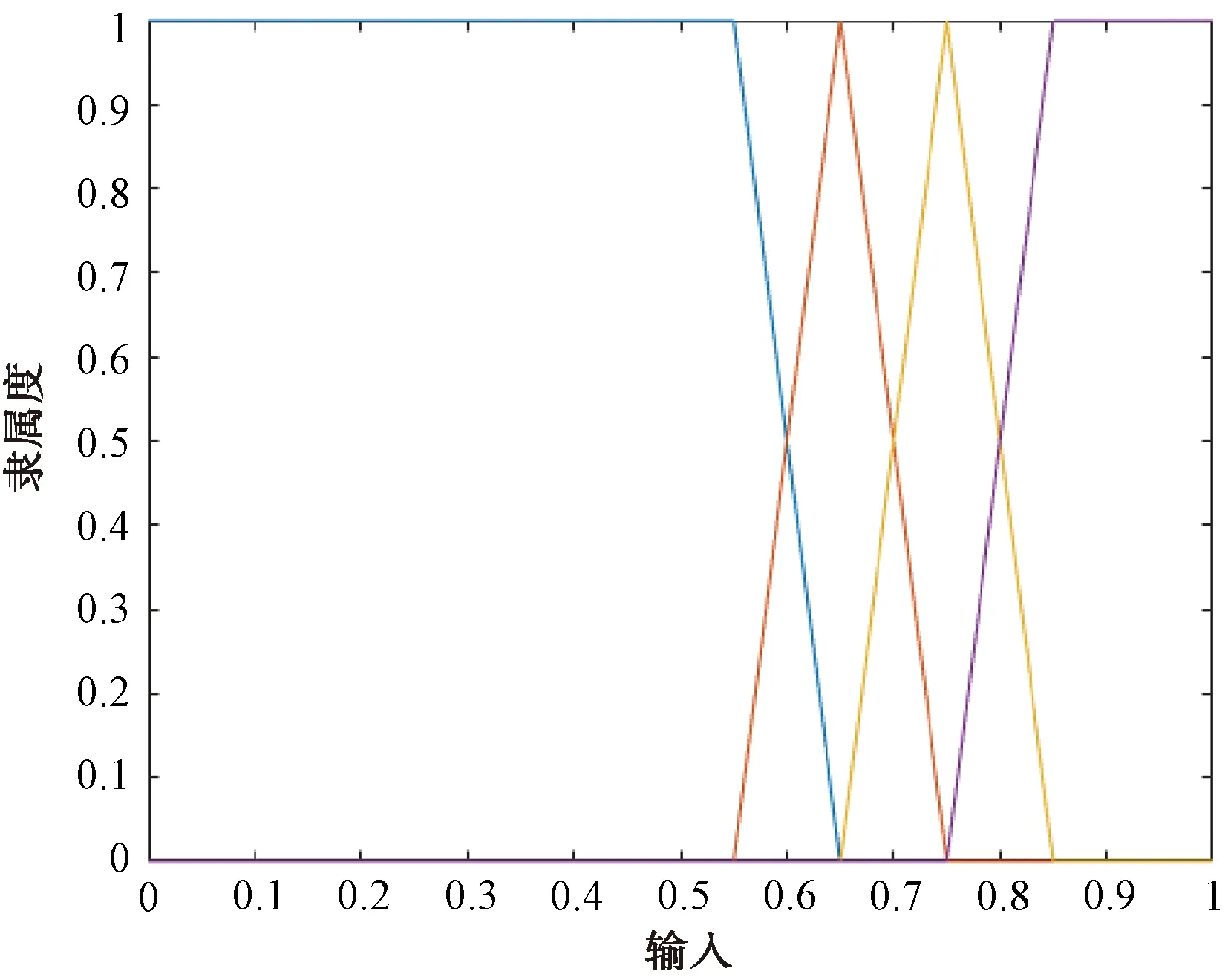
圖1 三角形和半梯形結合的隸屬函數

效能指標經過等極化處理后得到的等極化矩陣滿足隸屬函數的[0,1]定義域區間，在隸屬函數的作用下轉化成隸屬矩陣，有個等級，根據第個一級指標對應的二級指標集隸屬矩陣()×和二級單排序權重向量，計算一級指標評判向量：

=°=[,,…,],=1,2,…,

(7)

式中:°為模糊算子，有極大極小、乘積取大、加權平均等類型。

欺騙干擾設備效能是各種效能指標的綜合體現，因此采用加權平均型模糊算子。

基于一級指標評判向量構成的隸屬矩陣()×=[,,…,]和一級單排序權重向量，計算目標評判向量：

=°=[,,…,]

(8)

最后，結合目標評判向量和評價集合，得到綜合評估結果，對應評價區間，確定欺騙干擾設備效能評估的分數：

=

(9)

3 仿真分析

如表2所示，使用王月等人匯總的欺騙干擾設備-效能指標作為仿真輸入，其中包含3種欺騙干擾方案對應的效能指標，用于驗證方法的有效性。

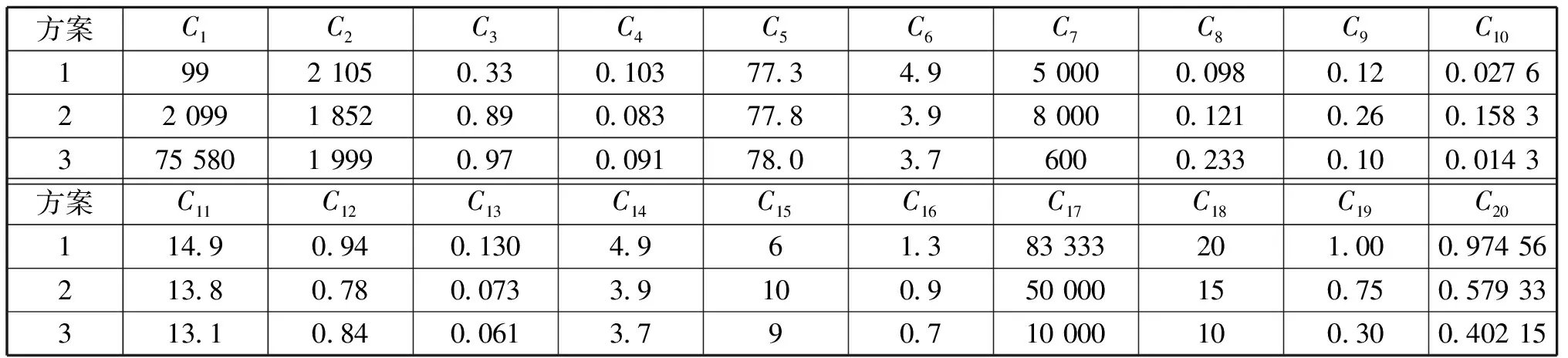
表2 欺騙干擾設備-效能指標矩陣

將效能指標進行等極化處理后得到等極化矩陣，如表3所示。從中可以看出每個指標的最優值1和最差值0都是出自于試驗數據而非人為設定，有效避免了人類主觀性帶來的分歧，具備對客觀試驗條件的適應性。

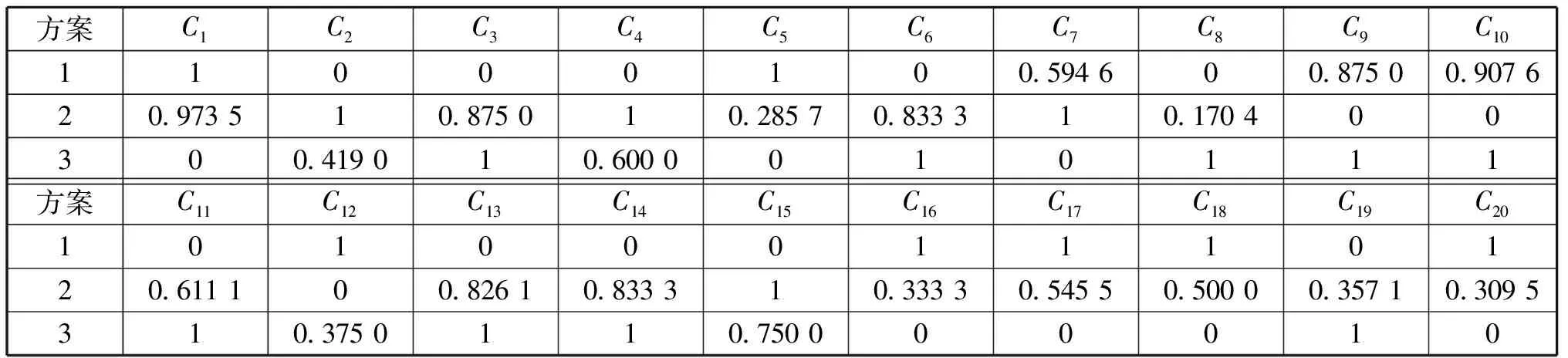
表3 等極化矩陣

基于CRITIC法進行指標定權，得到層次相對于層次的權重，如表4所示。

層次相對于層次中不同準則的指標權重如表5所示。綜合分析表4、表5可知：為各效能指標分配的權重比較接近，說明在關注關聯性和波動性的前提下，它們的重要程度相近。

表4 層次B的權重

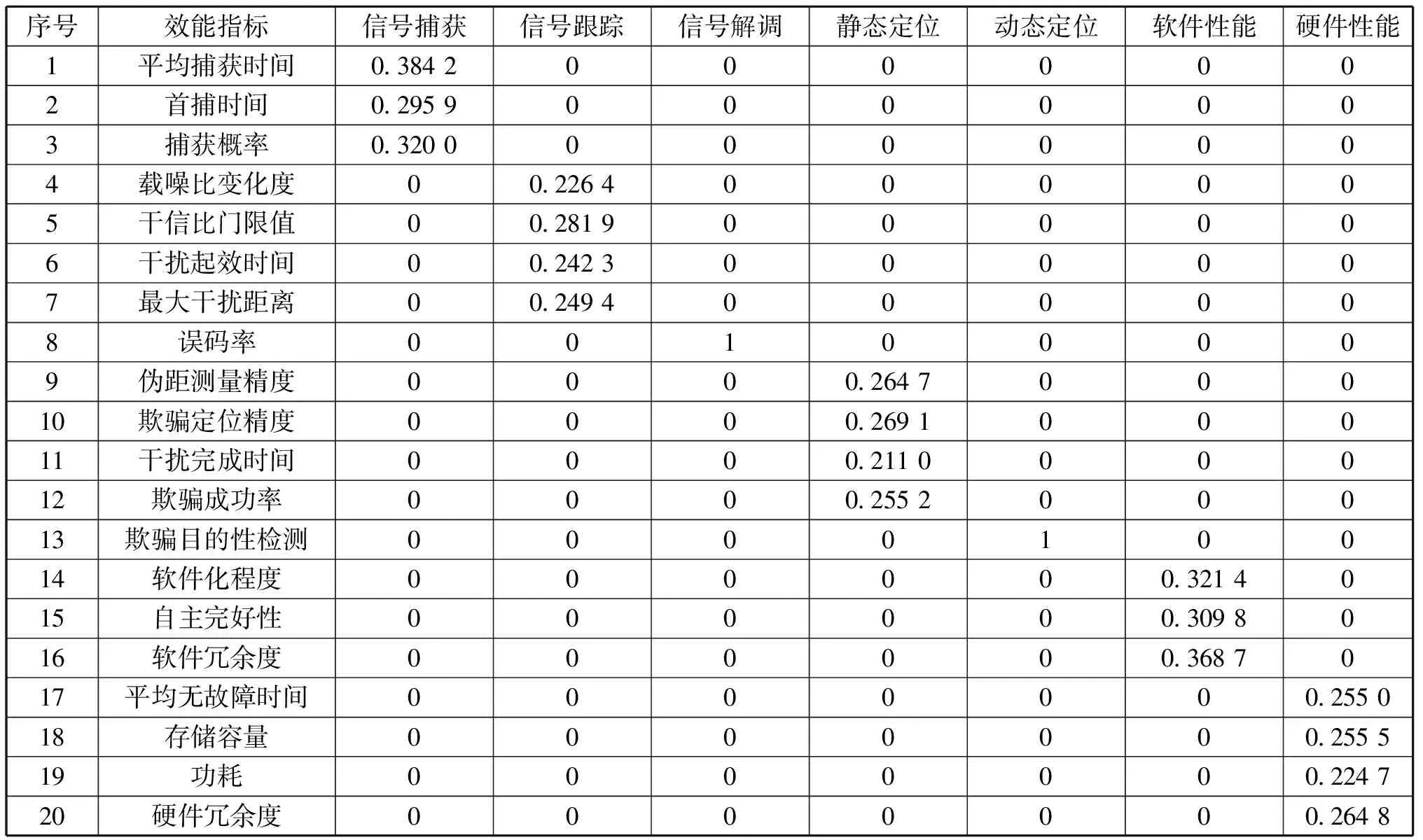
表5 層次C的權重

故經過模糊綜合評判后的結果為：

(方案1)=74847 3

(方案2)=71791 1

(方案3)=73761 6

欺騙干擾方案的優劣排序為：方案1>方案3>方案2，與王月等人的結論相同。這表明FAHP-CRITIC欺騙干擾設備效能評估方法能夠有效評估各方案的相對優劣，具有實用性。各方案的最終得分位于良好水平，比王月等人計算的分數略低，這主要是由于：(1)對效能指標進行等極化處理后，部分數據歸零；(2)采用CRITIC法進行客觀賦權，主要關注數據自身特點，為各指標分配的權重比較接近。

4 結束語

考慮到不同指標之間的關聯性和同一指標在多組數據中展現的波動性，避免賦權時引入主觀性，本文提出一種FAHP-CRITIC欺騙干擾設備效能評估方法，先建立多層級指標體系，接下來對指標進行等極化處理，然后使用CRITIC法為指標客觀賦權，最后使用模糊綜合評判法確定效能評分。通過計算機仿真得到的干擾方案效能評估結果與其他研究接近，驗證了方法的有效性，同時發現計算結果依賴數據自身，具備實用性。然而，實際中對效能指標賦權時還會考慮其獲取的難易程度、數據的準確性等因素，這些因素未能以數值的形式體現出來，無法融合到本文提出的方法中，是未來的研究方向之一。