含風光水多源互補電力系統的分布式抽蓄選址定容與優化調度

況 靜，蘭 洲，楊 愷，郭瑞鵬

（1.浙江大學 電氣工程學院，浙江 杭州310027；2.國網浙江省電力有限公司 經濟技術研究院，浙江 杭州310000）

0 引 言

風電、光伏和水電作為可再生能源，具有無污染、可持續等諸多優點，但其出力具有間歇性、波動性和隨機性等特點，給電網安全經濟運行帶來一定挑戰［1-2］，挑戰主要包括棄風棄光［3］、調峰調頻［4-5］、功角與電壓穩定［6］等問題。 研究表明，電網接入儲能系統是解決大規模可再生能源并網問題的有效途徑。 隨著抽水蓄能、氫儲能、空氣儲能等多種跨時空靈活性儲能技術的快速發展，儲能成本持續下降，尤其是分布式抽水蓄能成本較為低廉，在進行規劃時，對其進行最優選址可以有效地降低投資成本［7-8］。

抽水蓄能是主要的儲能形式，已成為調節頻率和電壓的靈活性電源［9］，在促進新能源消納方面具備極大的優勢。 抽蓄擁有“源網荷儲”四方面全要素特性，實質是電網的基本單元，在能源互聯網中必不可少，是推動能源轉型發展的重要支撐。 抽水蓄能電站可以為電網提供各種形式的安全保障輔助服務。 通常情況下抽蓄容量大、工況多、速度快、可靠性高、經濟性好［10］。 在當下“碳達峰、碳中和”的口號下，抽水蓄能可產生巨大的推動力，更好地服務高比例可再生能源并入電網，配合電網實現可再生能源大范圍內資源優化配置。 同時，因為抽蓄上下游水庫蓄水，抽水蓄能可利用這一特性與周邊生態和諧發展。

抽水蓄能因其容量大，運行調節靈活，無污染等特性被越來越多的運用于電網的優化調度中，在市場中具備一定的競爭力。 而國內外針對分布式抽水蓄能的選址定容問題也展開了很多的研究。 文獻［11］提出了考慮負荷響應的含風光抽蓄的海島微網優化配置模型，利用粒子群算法對微網中抽蓄選址定容進行了求解；文獻［12］通過成本效益分析實現了抽水蓄能運行成本最小的目標，確定風蓄聯合運行的控制策略，采用混合整數二階錐規劃方法求解模型。 文獻［13］以儲能容量、微網設備安裝成本與系統運行維護成本為目標，基于自適應遺傳算法，得到最優風、光、水等分布式電源協調控制方法以及該條件下的儲能系統配置容量和運行方式。 由于分布式抽水蓄能電站的選址定容優化問題需考慮電網的網架結構，其模型求解較為復雜，文獻［14］提出了一種改進多目標粒子群算法求解儲能選址定容問題。 文獻［15］提出一種儲能選址定容的雙層優化方案，外層通過遺傳算法求解，內層通過序列二次規劃算法求解。 但啟發式算法往往具有收斂速度慢、容易陷入局部最優等缺點。 所以探索有效的數值分析法很有必要。

本文主要研究建立計及電網網架約束的含風、光、水多源互補電力系統的分布式抽水蓄能選址定容規劃模型，在已知預規劃抽水蓄能電站的規劃總容量和備用選址的前提下，在備用選址范圍內對分布式抽水蓄能電站進行最優選址和容量配置。 綜合考慮電網運行安全與經濟成本等因素，重點解決抽水蓄能電站的選址定容問題，選擇合適的安裝位置和容量避免局部電網過載、過電壓或者欠電壓等問題，降低整個系統的運行成本，提高系統的穩定性和安全性。 以抽水蓄能有功控制、DG有功控制等方式，實現多源互補電力系統的優化調度。 本文利用二階錐松弛將所建模型轉化為凸規劃形式，從而獲得全局最優解以及加快求解速度，實現含風、光、水-分布式抽水蓄能聯合電力系統的優化調度，并通過算例驗證所提方法的有效性。

1 分布式抽水蓄能系統選址定容規劃模型

電力系統的抽水蓄能選址定容問題涉及到諸多方面的因素影響，實際上是個多目標優化的問題。 大量分布式電源接入電網，由于風、光等資源具備不確定性和波動性，所以其輸出電能的質量較差，當自身調控能力不足時需要向外購電以滿足負荷需求。 而分布式抽水蓄能系統可以一定程度上改善這些問題。 本文針對分布式抽水蓄能電站的選址定容問題進行研究。

1.1 目標函數

確定模型的目標函數，主要考慮網絡損耗最小、風光水棄電量最小，主網購電成本最小，運行總成本如下式：

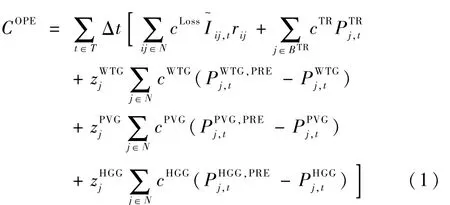
式中：cLoss、cTR、cWTG、cPVG、cHGG分別為網損價格、主網購電價格、風電棄電、光伏棄電和水電棄電懲罰價格分別為風電、光伏和水電預測出力分別表示節點j是否安裝相應設備水 的 實 際 出 力表 示 向 主 網 購 電 量；BTR表 示與主網相連節點的集合；Δt表示時間間隔；T表示調度總時間區間；BTR表示與主網相連節點集合；N表示總節點集合。分 別 表 示 風 光

1.2 約束條件

在進行分布式抽水蓄能電站的選址定容時，除了考慮電力系統的運行約束外，還需要考慮抽水蓄能電站的抽水/發電功率和容量平衡等約束。

1.2.1 基于二階錐松弛的交流潮流約束

錐優化作為凸優化的一種，其錐結構的求解域使得求解效率大大提升，因此被廣泛應用到控制論、經濟學、博弈論、數值優化等多方面。 二階錐規劃（second order cone programming， SOCP）作為錐優化理論的一種特殊形式，定義為在一個放射空間以及有限二階笛卡爾積二者之間的交集中，進行線性函數極值的優化求解，具有凸規劃的所有特征，且計算便捷，因此日益得到廣泛關注。

SOCP的數學形式表示如下：

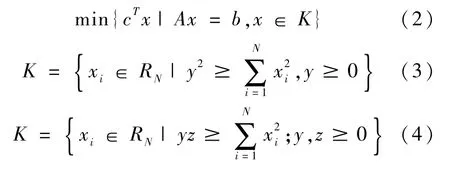
式中：變量x∈RN，b∈RN，c∈RN，AM×N∈RM×N；K可為上式所示的二階錐或者所示的旋轉二階錐的形式。

交流潮流模型［19］如下：

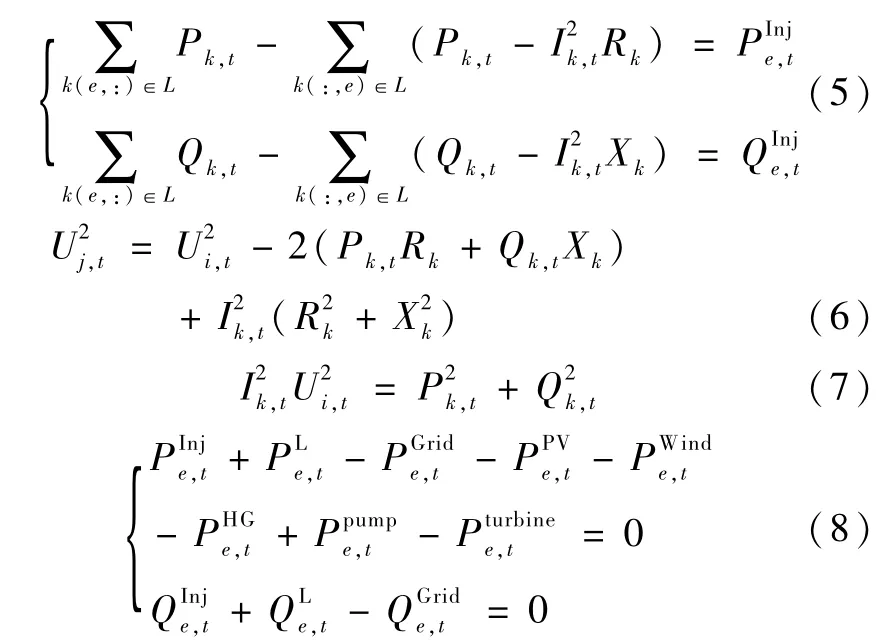
式中：下標e表示節點；下標i和j表示支路的起點和終點；L 表示支路集合；k（e，：） 表示以節點e為首端的支路k；k（：，e） 表示以節點e為末端的支路k；Pk，t、Qk，t和Ik，t分別表示支路k始端流向末端的有功功率、無功功率和電流；Rk、Xk表示支路k的電阻 和 電抗；Ui，t為 節 點 電壓；PIen，jt、QIen，jt為 節 點 注入有功和無功。PLe，t為 節 點有 功 負 荷；PGe，rtid為節 點向外網有功購電；QLe，t為 節點無功負荷；QGe，rtid為 節點向外網無功購電。

根據文獻［16］ -［18］ 可知，使用式（9） 的變量，替換交流潮流約束中式（5）（6）（7）：

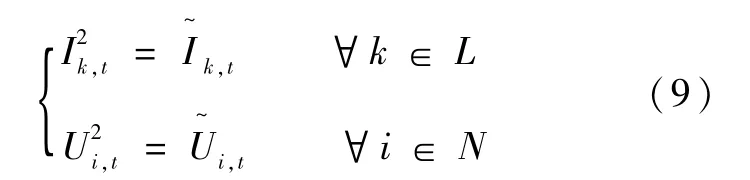
交流 潮 流 約 束 中 式（5）（6）（7） 轉 化 為 式（10）（11）（12），如下所示：

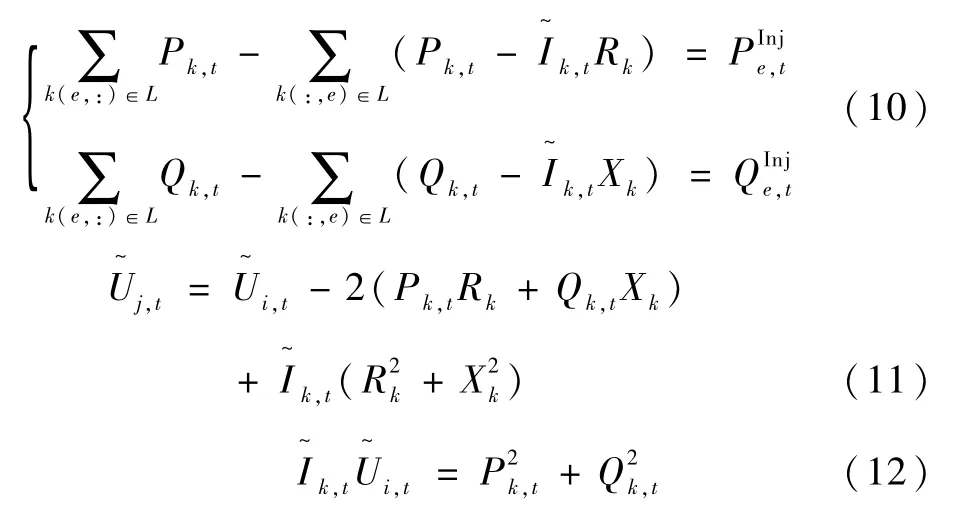
對式（12） 進行二階錐松弛［16］，可得式（13）。

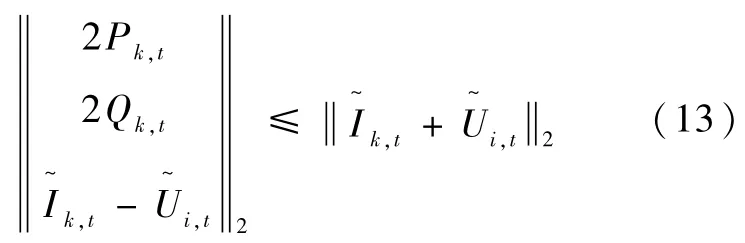
所以式（8）（10）（11）（13） 構成二階錐交流潮流約束。通過二階錐松弛，將分布式抽水蓄能系統規劃模型轉化為混合整數二階錐規劃模型，模型便于高效求解。通過Gurobi、Cplex商業算法包以及內點法等數值算法都可以方便高效地對SOCP問題進行求解，且由于其凸規劃的本質，求解結果一定為全局最優解。因此，近年來SOCP己經被廣泛應用于電力系統中的選址定容、組合優化等領域。

1.2.2 分布式電源約束

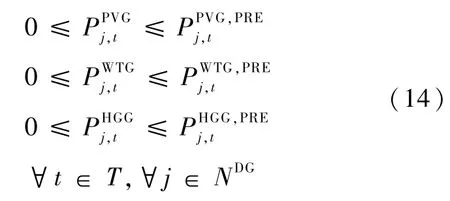
式中：NDG為DG節點集合。

1.2.3 抽水蓄能電站約束

1.2.4 系統安全約束

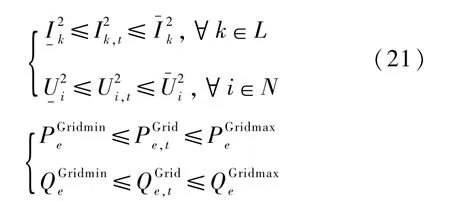
2 分布式抽水蓄能系統選址定容規劃策略

在當下發展新能源，保護生態環境的背景下，發展分布式抽水蓄能電站就變得越來越重要。 因此，利用現有的資源，考慮地形的不同，因地制宜地展開對分布式抽水蓄能電站的規劃建設，是促進能源轉型的有效方式。

抽水蓄能電站的地理位置以位于負荷中心地區并接近樞紐變電所最佳，因為該位置為抽水蓄能電站提供了很好的接入系統條件，使得送、受線路最短，輸電損失最小。

本文提供了一種分布式抽水蓄能系統選址定容策略，具體如下：

（1）對所需新建分布式抽水蓄能電站地區的發電情況和用電情況進行調研，根據其歷史數據得出該地區所需分布式抽蓄總容量；

（2）對待研究地區的地形進行調研，充分考慮當地的地質條件，選取幾個合適的分布式抽水蓄能電站可建設的點；

（3）在已知預規劃分布式抽蓄總容量和備用選址的條件下，以網損最小、棄風光率最小和向主網購電成本最小為目標，對幾個可能的規劃方案進行計算，并比較它們的經濟性，得出最優的規劃方案；

（4）將全年分為夏季、冬季和春秋過渡季三個場景，計算全年的經濟成本。 其具體策略流程圖如圖1 所示。

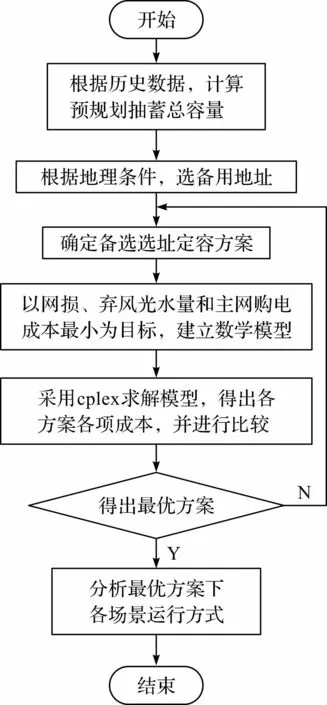
圖1 策略流程圖

3 算例分析

3.1 參數設置

結合以上所建立的計及網絡約束的風、光、水-分布式抽水蓄能選址定容規劃模型，展開算例分析來驗證模型和方法的有效性。 本章算例以IEEE33 標準節點模型為例，在基礎網絡上添加了風機、光伏、小水電、抽水蓄能電站等，網絡參數詳見文獻［19］。 在IEEE33 節點上增加2 座裝機容量為1 MW 光伏電站、1 座裝機容量為1 MW 風電站、4 座裝機容量為0.5 MW 水電站。 網損價格為100 元/MWh，主網購電成本為500 元/MWh，棄風、光、水懲罰成本為400 元/MWh。

研究建立在已知預規劃抽水蓄能電站的規劃總容量和備用選址的前提下，對分布式抽水蓄能電站進行最優選址定容。 所以假定備用選址為節點15、18、32。 設計以下幾種規劃方案：（1）從3個備用選址中選1 個節點只建1 座抽蓄電站，其分布式抽蓄參數如表1 所示；（2）從3 個備用選址中選2 個節點建2 座抽蓄電站，其分布式抽蓄參數如表2 所示。

表1 方案1 抽水蓄能參數

表2 方案2 抽水蓄能參數

本文算例將全年分為3 個場景，即夏季、冬季和春秋過渡季，選取3 個場景的3 個典型日的風、光、水和負荷出力曲線進行計算，計算一整年的總成本。

本文算例選取分布式抽水蓄能電站參與儲能系統的選址定容規劃。 將一天24 小時每隔1 小時取一個點，共24 個點，其中各場景的風、光、水和負荷的曲線如圖2 -圖5 所示。

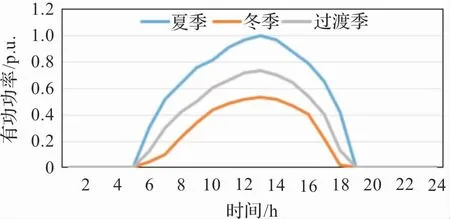
圖2 光伏出力曲線

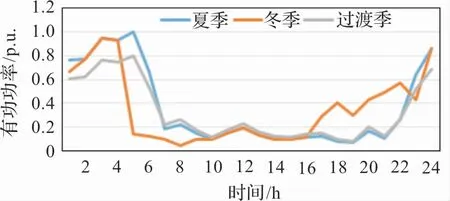
圖3 風電出力曲線

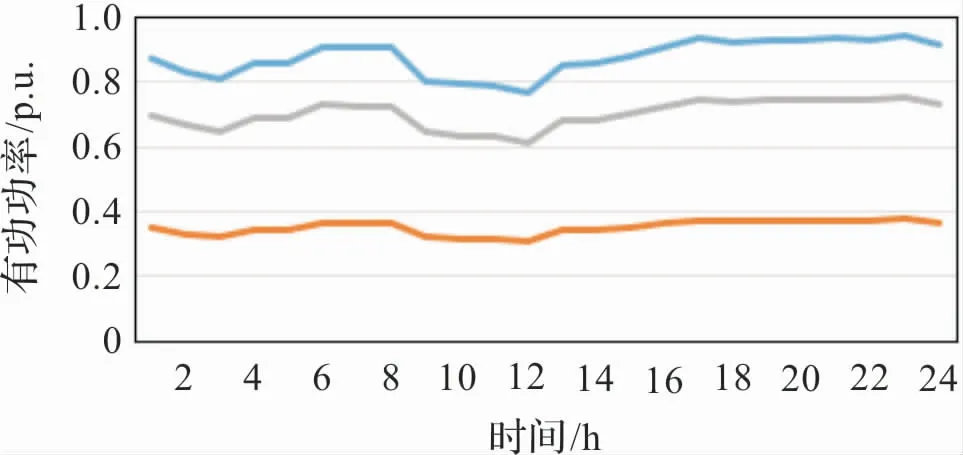
圖4 水電出力曲線

圖5 典型負荷曲線

3.2 結果分析

（1）成本比較分析

針對規劃方案1 和2，設計以下6 種具體方案，考慮夏季、冬季和春秋過渡季三個場景，計算全年的總成本，具體如表3 所示。

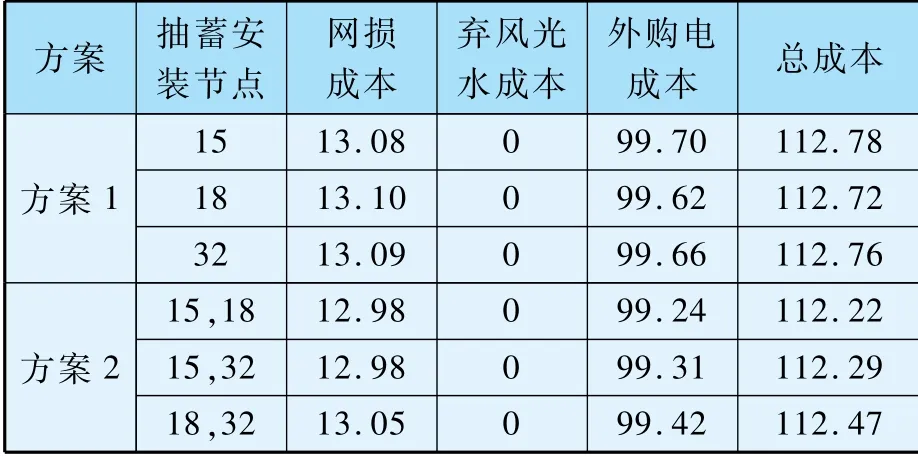
表3 方案成本分析 單位：萬元

已知該系統在未添加分布式抽蓄時，其一年的總成本為161.47 萬元，其中外購電成本為137.11 萬元，在添加了分布式抽蓄后，其總成本約降低了31%，可見添加分布式抽蓄后具備很好的運行經濟性。 從表3 中可以看出，在添加了分布式抽水蓄能電站后，含風、光、水的多源互補電力系統棄風光率降為0，實現了可再生能源的最大消納，同時其外購電成本也大大降低，實現了系統自身的優化調度。 對比幾種方案可知，將抽水蓄能電站建在節點15 和節點18 時，系統的總成本最低。 對比方案1 和方案2 可知，從3 個節點中選出2 個點建分布式抽蓄對系統的運行來講更加經濟，這是因為多個抽蓄電站相互配合時，對源荷不平衡的響應更加靈活，同時分布式抽蓄接入多個負荷中心時，可使得輸電損失更小。

（2）分布式抽蓄最優選址定容運行分析

針對得出的最優分布式抽蓄規劃結果，分析其在夏季、冬季和春秋過渡期3 個場景的優化調度，3個場景的分布式抽蓄抽水/發電運行方式如圖6 -圖8 所示，3 個場景下的外購電結果如圖9 所示。

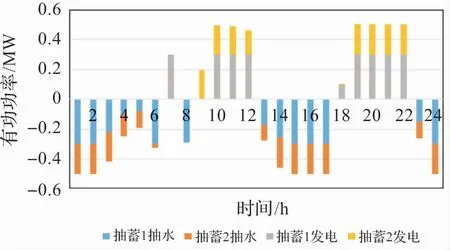
圖6 夏季分布式抽蓄調度結果

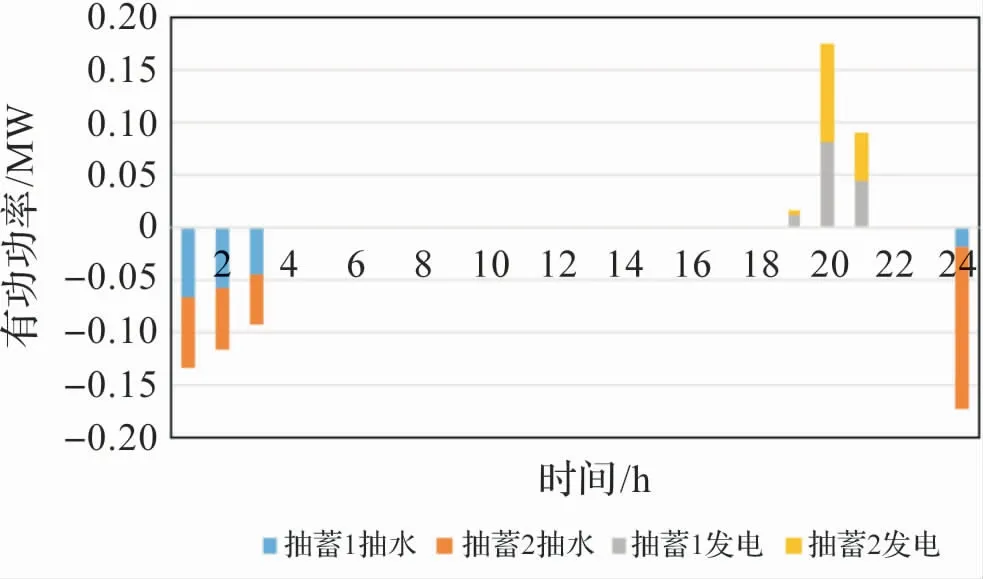
圖7 冬季分布式抽蓄調度結果

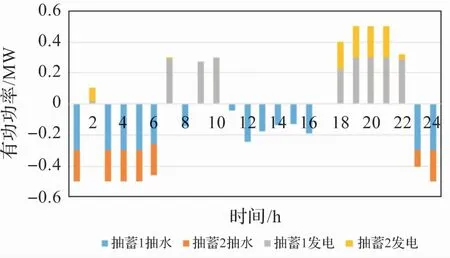
圖8 春秋過渡季分布式抽蓄調度結果

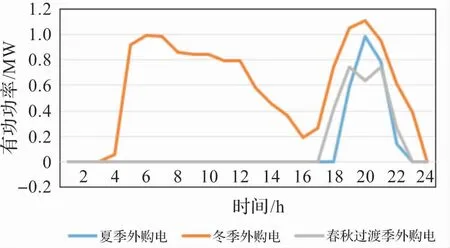
圖9 3 種場景下系統外購電情況

從圖6 -圖9 可以看出，在夏季，23：00 到次日5：00，此時夜間負荷出力較小，而風電此時出力較大，所以分布式抽蓄電站抽水以消納多余的發電量；9：00 -12：00 負荷不斷攀升，而光伏出力也在不斷攀升，所以分布式抽蓄發電以補償發電量不足的情況；12：00 -16：00，負荷不斷下降，而此時光伏出力仍較大，所以分布式抽蓄抽水消納多余光伏出力；19：00 -22：00，負荷出現回升，光伏出力降為0，風電出力逐漸上升但不足以支撐負荷，此時分布式抽蓄發電以補償負荷，不足時仍需外購電以滿足負荷需求。 由于夏季來水量較大，所以水電基本承擔基荷作用。

在冬季，由于光伏出力較小，而來水較少也導致水電站發電量不足，所以系統白天需要大量外購電以滿足負荷需求，外購電成本基本在冬季；在夜間風電出力上升時，分布式抽蓄抽水儲存一定的電量。

在春秋過渡季，負荷相對較小，其分布式抽蓄運行狀況與夏季基本相同，不再贅述。

綜上所述，分布式抽蓄主要作用在夏季和春秋過渡季，而冬季風、光、水發電量不足需要外購電，從而產生一定量的外購電成本。

4 結 論

為實現可再生能源的最大消納，有必要研究可以促進其消納的各種手段，其中利用分布式抽水蓄能電站進行調節是很好的手段。 本文研究建立在已知預規劃抽水蓄能電站的規劃總容量和備用選址的前提下，對分布式抽水蓄能電站進行最優選址定容。 通過對可能的選址方案進行枚舉，對比分析不同方案下的總成本。 得出以下結論：

（1）建立的計及電網網架約束的含風、光、水多源互補電力系統的分布式抽水蓄能選址定容規劃和優化調度模型，以網損最小、棄風、光、水量最小、向主網購電成本最小為優化目標，解決分布式抽水蓄能電站的選址定容問題。

（2）結果表明多個抽蓄電站相互配合時，調節更加靈活，同時分布式抽蓄接入多個負荷中心時，可使得輸電損失更小。

（3）利用二階錐松弛將所建模型轉化為凸規劃形式，從而獲得全局最優解以及加快求解速度。

本文的算例建立在電網網架是輻射狀結構的基礎上，在今后的研究中，將對基于二階錐松弛的環狀電網潮流約束進行研究。